5.1.3. Непрерывность вектор функции

r(t) определена на [,] и t₀(,)

r(t) непрерывна, если r(t) = r(t₀)

Аналогично определяется непрерывность справа, слева.

Непрерывность на множестве.

Свойства

p(t) , q(t) , (t) непрерывны в точке t₀  непрерывны p(t) + q(t), (t)p(t) ,( p(t), q(t)), [ p(t) , q(t)] .

5.1.4. Дифференцируемость вектор функции

Пусть r(t) определена в окрестности точки t₀.

Производной в точке t₀ называется нижеследующий предел, если он существует,

r(t)=(r(t) – r(t₀))/(t – t₀).

Теорема. Производная вектор функции r(t) в точке t₀ существует тогда и только тогда, когда существуют x(t₀), y(t₀), z(t₀) и r(t₀)=.

Утверждение следует из критерия существования предела вектор функции.

Замечание. Если у r(t) существует r(t₀) в точке t₀, то r(t) непрерывна в этой точке.

Определение. Векторная функция r(t) называется дифференцируемой в точке t₀, если в некоторой окрестности этой точки выполняется равенство

r(t) - r(t₀) =a(t – t₀) +(t) (t – t₀), (1)

где (t) = 0.

Векторная функция a t = a (t – t₀) = a dt называется дифференциалом функции r(t) в точке t₀ и обозначается dr = a dt .

Условие (1) можно записать в координатной форме

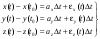(2)

где a =(a_x, a_y, a_z),  = (_x , _y , _z ) .

Теорема. Дифференцируемость r(t) в точке t₀ эквивалентна дифференцируемости в точке t₀ координат функции r(t).

Следствие. Для дифференцируемости r(t) в точке t₀ необходимо и достаточно существование r(t₀).

Геометрический смысл производной r(t):

Рис. 4.27

5.1.5. Правила дифференцирования вектор функций

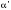1) ( r) =r +  r.

2) (r₁ + r₂ ) = (r₁ + r₂ ).

3) (r₁ , r₂ ) = (r₁ , r₂ ) + (r₁ , r₂ ).

Для краткости будем рассматривать плоские вектора.

r₁= , r₂=. Тогда (r₁,r₂)=

и (r₁ , r₂ )=

=

==

=(r₁ , r₂ ) + (r₁ , r₂ ).

4) [r₁ , r₂ ] = [r₁ , r₂ ] + [r₁ , r₂ ].

5.1.6. Гладкие кривые Определение. Кривая

 : tT

называется непрерывной, если непрерывны x(t), y(t), z(t). (Можно определять непрерывность в точке или на множестве).

Для заданной параметризации t[ , ] начало кривой – точка A(x(),y(),z()), конец кривой – точка B(x(),y(),z()).

Замкнутая кривая это кривая, у которой конец совпадает с началом.

Кривая называется непрерывно дифференцируемой, если функции x(t), y(t), z(t) непрерывно дифференцируемы.

Гладкой называется кривая, которая непрерывно дифференцируема и для которой выполнено условие t : r(t)0.

Кусочно гладкая кривая – кривая, которая непрерывна и состоит из конечного числа гладких кусков.

5.2 Длина кривой

Длина кривой. Спрямляемость.

5.2.1.Спрямляемая кривая

Разбиенем отрезка [,] называется набор точек t₀ , t_{1 ,}…. t_n таких, что =t₀< t₁<….< t_n=. Разбиение отрезка будем обозначать ={=t₀< t₁<….< t_n= } .

Пусть  : r(t) -непрерывно дифференцируемая на [,] кривая и ={=t₀< t₁<….< t_n= } – некоторое разбиение отрезка [,]. Для данного разбиения можно построить вписанную ломаную с узлами в точках A_k=(x(t_k), y(t_k), z(t_k)), k=0,1,…,n. Радиус вектор в точку A_k обозначим r_k. Длину ломаной обозначим (,)

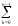(,)=|r_k+1 – r_k|

Рис. 5.1

рисунок для плоского случая

Определение. Кривая  называется спрямляемой, если конечна точная верхняя грань , где точная верхняя грань берется по всевозможным разбиениям  отрезка [,]. Эта величина s называется длиной кривой .

Пример непрерывной, не спрямляемой кривой.

Рис. 5.2

Длина основания очередного прямоугольника равна половине длины основания соседнего прямоугольника справа. Число звеньев ломаной, вписанной в прямоугольник берется таким, чтобы длина участка ломанной, попавшей в прямоугольник была > 1.

Теорема 1. Кривая, составленная из двух спрямляемых кривых спрямляема и ее длина равна сумме длин исходных компонент.

Доказательство. Пусть  = +. Для любого разбиения  кривой  существуют разбиения ,  кривых ,  такие, что ( , )  ( , )+( , ) . На рисунке на участке стыка двух кривых хорда AB заменяется на две хорды AC и CB. Все остальные хорды разбиения кривой  оставляем без изменения

Рис. 5.3

Так как AB  AC + CB , то отсюда получаем соотношение для длин кривых s  s + s. С другой стороны любая пара ,  разбиений кривых ,  образует разбиение  кривой , так что ( , ) = ( , )+( , ) , поэтому справедливо обратное неравенство s  s + s.

Теорема 2. Если кривая  непрерывно дифференцируема, то она спрямляема и ее длина s удовлетворяет неравенству

,

где ,,

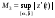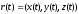, ,,, t[,].

Доказательство. Пусть ={=t₀<t₁<…<t_n=}, тогда по теореме Лагранжа

|r(t_k+1 –r(t_k)|==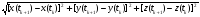

= и

( - ) = ( , )=

==

= ( - ).

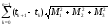Для верхней грани получим ( - )  s  ( - ).

Откуда и следуют требуемые неравенства.

Теорема 3. Если кривая  гладкая, то длина дуги s(t) от начала кривой до точки, соответствующей значению параметра t, является строго монотонно возрастающей, непрерывно дифференцируемой функцией и

=|r(t)|

Доказательство. На участке [t,t+t] по теореме 2 выполнены неравенства

(1)

Рис. 5.4

Требуемое равенство получится при переходе к пределу при t0, если учесть, что левая и правая части (1) будут иметь общий пределНапример, Строгое монотонное возрастание функции s(t) следует из условия выполненного для гладкой кривой.

Следствие 1. Для гладкой  можно выбрать в качестве параметра длину дуги от начала кривой до данной точки s=s(t).

Действительно, для этой функции существует обратная t=t(s) и, следовательно, (t)= (t(s))

В этом случае |dr/ds|=|r(t)t(s)| =|s(t)t(s)|==1.

Следствие 2. dt, ds²=dx²+dy²+dz², ds – элемент длины дуги.

Пример. Длина цепной линии y = ch x .

Параметризацию кривой выберем в виде x = t, y = ch t , t[0, t₀].

Рис. 5.5

s(t)=|r(t)|=|i + sh t j|==ch t. Таким образом, s(t) = (sh t) . Согласно следствия из теоремы Лагранжа s(t)=sh t + C. s(0)=0  s(t) = sh t .