4.1.3.Основные правила дифференцирования

1. f=const, f=0, df=0x=0.

2. f=u+v, f=u+v, df = du+dv.

3. f=uv, f=uv+vu, df = u dv + v du.

Следствие. (cf(x))=cf(x), (c₁f₁(x)+…+c_nf_n(x))= c₁f₁(x)+…+ c_n f_n(x)

4. f=u/v, v(x₀)0 и производная существует, то f=(uv-vu)/v².

Для краткости будем обозначать u=u(x), u₀=u(x₀), тогда

=

Переходя к пределу при x 0 получим требуемое равенство.

5. Производная сложной функции.

Теорема. Если существуют f(x₀), g(x₀) и x₀=g(t₀), то в некоторой окрестности t₀ определена сложная функция f(g(t)), она дифференцируема в точке t₀ и

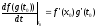
Доказательство.

f(x) - f(x₀)=f(x₀)(x-x₀)+(x)(x-x₀), xU(x₀).

Можно считать (x₀)=0.

f(g(t))- f(g(t₀))= f(x₀)( g(t)- g(t₀))+( g(t))( g(t)- g(t₀)).

Поделим обе части этого равенства на (t - t₀) и перейдем к пределу при tt₀.

6. Вычисление производной обратной функции.

Теорема. Пусть f непрерывна и строго монотонна на [a,b]. Пусть в точке x₀(a,b) существует f(x₀) 0, тогда обратная функция x=f ^-1(y) имеет в точке y₀ производную, равную

Доказательство. Считаем f строго монотонно возрастающей, тогда f ^-1(y) непрерывна, монотонно возрастает на [f(a),f(b)]. Положим y₀=f(x₀), y=f(x), x - x₀=x,

y - y₀=y. В силу непрерывности обратной функции y0  x0, имеем

. Переходя к пределу, получим требуемое равенство.

7) Производная четной функции нечетна, производная нечетной функции четна.

Действительно, если x - x₀ , то -x x₀, поэтому

Для четной функции 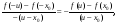для нечетной функции

.

4.1.4.Производные элементарных функций

1) f=const, f(x)=0.

2) f(x)=x, f(x)=1.

3) f(x)=e^x, f(x)= e^x ,

4. f(x)=a^x, (a^x) = a^x ln a.

5. ln a.

6. f(x)=ln x ,,

Следствие. (производная четной функции нечетна)

6)

7) (x^)=x^{ -1}, x>0, x^=e^{ ln x}.

8) (sin x)=cos x,

9) (cos x)=-sin x, (cos x)=(sin(x+/2))= cos(x+/2)=-sin x.

10) (tg x)=1/cos²x.

11) (ctg x)=-1/sin²x.

12).

.

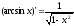13) .

.

14) .

.

15)

.

16. sh x, ch x.

.

.

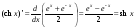4.1.5. Логарифмическое дифференцирование

f(x), , откуда следует, что f(x)=f(x)(ln f(x)) .

Ту же формулу можно получить иначе f(x)=e^{ln f(x)}, f=e^{ln f(x)}(ln f(x)).

Пример. Вычислить производную функции f=x^x.

=x^x= x^x= x^x= x^x(ln x +1).

4.1.6.Функции, заданные параметрически

Геометрическое место точек на плоскости

.

будем называть графиком функции, заданной параметрически. Говорят также о параметрическом задании функции.

Замечание 1. Если x, y непрерывны на [,] и x(t) строго монотонна на отрезке [,] (например, строго монотонно возрастает), то на [a,b] , a=x(), b=x() определена функция f(x)=y(t(x)), где t(x) – обратная к x(t) функция. График этой функции совпадает с графиком функции

.

Если область определения [,] параметрически заданной функции можно разбить на конечное число отрезков [_k ,_k ], k=1,2,…,n, на каждом из которых функция x(t) строго монотонна, то параметрически заданная функция распадается на конечное число обычных функций f_k(x)=y(t ^-1(x)) с областями определения [x(_k ), x(_k )] для участков возрастания x(t) и с областями определения [x(_k), x(_k )] для участков убывания функции x(t). Полученные таким образом функции называются однозначными ветвями параметрически заданной функции.

На рисунке показан график параметрически заданной функции

При выбранной параметризации область определения [0,2] разбивается на пять участков строгой монотонности функции sin(2t), именно: t t, t, t , и, соответственно, график распадется на пять однозначных ветвей, соответствующих этим участкам.

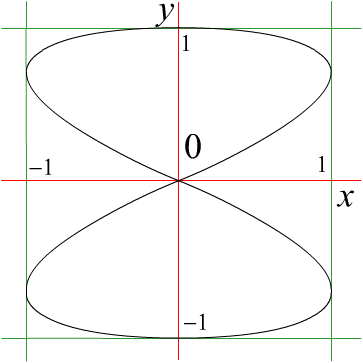
Рис. 4.4

Рис. 4.5

Можно выбрать другую параметризацию того же геометрического места точек

.

В этом случае таких ветвей будет только четыре. Они будут соответствовать участкам строгой монотонности t , t , t , t функции sin(2t).

Рис. 4.6

Четыре участка монотонности функции sin(2t) на отрезке длинной .

Рис. 4.7

Изображение обоих графиков на одном рисунке позволяет приблизительно изобразить график параметрически заданной функции, используя участки монотонности обеих функций.

Рассмотрим для примера первую ветвь, соответствующую отрезку t . На концах этого участка функция x=sin(2t) принимает значения -1 и 1 , поэтому эта ветвь будет определена на [-1,1] . После этого нужно смотреть на участки монотонности второй функции y=cos(t), у нее на два участка монотонности . Это позволяет сказать, что у первой ветви имеется два участка монотонности. Найдя концевые точки графика можно соединить их прямыми для того, чтобы обозначить характер монотонности графика. Проделав это с каждой ветвью, получим участки монотонности однозначных ветвей графика (на рисунке они выделены красным цветом)

Рис. 4.8

Первая однозначная ветвь f₁(x)=y(t(x)) , соответствующая участку будет определена для x[-1,1]. Первая однозначная ветвь t, x[-1,1].

Все остальные три ветви будут иметь областью определения тоже множество [-1,1].

Рис. 4.9

Вторая ветвь tx[-1,1].

Рис. 4.10

Третья ветвь t x[-1,1]

Рис. 4.11

Четвертая ветвь tx[-1,1]

Рис. 4.12

Замечание 2. Одна и та же функция может иметь различные параметрические задания. Различия могут касаться, как самих функций x(t), y(t) , так и области определения [,] этих функций.

Пример различных параметрических заданий одной и той же функции

и t[-1, 1].

Замечание 3. Если x,y непрерывны на [,] , x(t)- строго монотонна на отрезке [,] и существуют производные y(t₀), x(t₀)0, то существует f(x₀)=.

Действительно, .

Последнее утверждение распространяется и на однозначные ветви параметрически заданной функции.