
Матан проверенный Анастасией Байковой
.docx|
1. Первообразная, неопределённый интеграл, их определения и свойства. Таблица основных интегралов. Определение: Функция F(x) называется первообразной для f(x) на ]a,b[, если в любой точке ]a,b[ F дифференцируема и выполняется соотношение: F’(x)=f(x). Замечание: Если F(x) – первообразная для f(x) на заданном промежутке, то F(x) + C; C R – тоже первообразная. Доказательство: F’(x) = f(x) – по условию (F(x)+C)’ = F’(x)+0 = f(x) Вывод: Если функция имеет первообразную, то она имеет их бесконечное множество. Теорема. Все первообразные функции для f(x) отличаются на постоянную. Доказательство:
Пусть f(x)
имеет F1(x)
и F2(x),
Определение: Множество всех первообразных для f(x) на ]a,b[ называется неопределённым интегралом от этой функции на ]a,b[. ∫f(x)dx; Таким образом, если F(x) задано первообразной f(x) на ]a,b[ то по определению: ∫f(x)dx = {F(x) + C, CR. Операция нахождения неопределённого интеграла от f(x) называется интегрированием f(x). Свойства: 1) d∫f(x)dx = f(x)dx; d(F(x))=F’(x)dx =f(x)dx=d(∫f(x)dx); 2)∫dF(x)=F(x)+C; dF(x) =F’(x)dx=f(x)dx; ∫f(x)dx=F(x)+C; 3)∫(f(x) ±g(x))dx=∫f(x)dx±∫g(x)dx; Доказательство. Возьмём производную от правой части: (∫f(x)dx±∫g(x)dx)’=(∫f(x)dx)’±(∫g(x)dx)’=f(x)±g(x); Таким образом ∫f(x)dx±∫g(x)dx является первообразной f(x)±g(x). 4)∫k*f(x)dx=k∫f(x)dx, k=const; Доказательство. Возьмём производную от правой части; (k∫f(x)dx)’=k(∫f(x)dx)’=k*f(x); Табличные
интегралы: 1)
∫0dx=c;
2) ∫1dx=∫dx=x+C;
3) ∫xαdx=(xα+1/α+1)
+ C
(α≠ -1) 4) ∫ (-1<x<1)
11)∫ 1.3Методы интегрирования: 1. Интегрирование подстановкой (замена переменной). Теорема: пусть 1)f(u) & u=φ(x) определены каждая на некотором промежутке. 2)Имеет смысл сложная функция f(φ(x)). 3)Функция φ(x)-дифференцируема тогда, если f(u) имеет первообразную, т.е. ∫f(u)du=F(u)+C (1), то f(φ(x))φ’(x) имеет первообразную F(φ(x)) и => ∫f(φ(x))φ’(x)dx=F(φ(x))+C (2). Доказательство:F(u)
определена на том же интервале, что и
f(u).
По условию имеет смысл f(φ(x))
и значит F(φ(x)).
По правилу дифференцирования получим:
∫f(u)du
и подставить u=φ(x),
или, наоборот, вместо ∫f(u)du
вычислить ∫f(φ(x))φ’(x)dx
и сделать подстановку x= (3) – формула с подстановкой, (4) – формула замены переменной. 2. Интегрирование по частям. Теорема:
если u(x)
и v(x)
дифференцируемы на некотором промежутке
и Доказательство: по правилу дифференцирования произведения d(uv)=vdu+udv и значит udv=d(uv)-vdu. Ввиду равенства дифференциалов (производных), будут равны и интегралы. ∫udv=uv+∫vdu, т.к. ∫d(uv)=uv+C.
|
|
|
|
2. Интегрирование рациональных функций посредством их разложения на сумму многочлена и простейших дробей четырёх типов и последующего интегрирования. f(x)= Правильно-рациональные дроби: 1) Теорема:
пусть
|
|
2.2 Интегрирования рациональных дробей. ∫ 1.∫ Iλ= Вывод: всякая рациональная дробь с вещественным коэффициентом интегрируется в элементарных функциях. |
2.3 Интегрирование некоторых иррациональных функций. Определение:
функция
вида R(x,y,z)
=
Пример:
1)f(x)= Интегралы
вида:
|
|
3. Определение интеграла Римана и интегрируемой функции. Теорема об ограниченности интегрируемой функции, необходимое условие интегрируемости. Определение:
пусть [a,b]
– заданный отрезок, разбиением Т
отрезка [a,b]
называется
Интегрируемая сумма: пусть на [a;b] определена f(x) и пусть T задано разбиением отрезка. На каждом из отрезков разбиения зафиксируем точки ξiє[xi-1;xi] Определение:
σ(T,ξi)= |
3.2
Определение:
f(x)
называется интегрируемой по Риману
на [a;b],
если
конечный предел I
интегральных сумм этой функции при
δT->0.
Этот предел называется определённым
интегралом от f(x)
на [a;b]
и обозначается: I= Теорема: если f(x) интегрируема на [a;b] , то она ограничена на [a;b]. Доказательство:
пусть f(x)
– неограниченна на [a;b].
Зафиксируем некоторое разбиение
T={x0;x1;…;xn}
этого отрезка, т.к. f(x)
неограниченна на [a;b]
тогда она неограниченна хотя бы на
одном из отрезков разбиения (пусть
[x0;x1])
. Составим интегральную сумму
ξi[xi-1;xi](i=2,3…n)
σ(Т,ξi)=f(ξi)Δx1+ Замечание: условие ограниченности является необходимым, но не является достаточным. |
|
4.Верхняя и нижняя сумма Дарбу и их свойства. Пусть
f(x)
ограничена на [a;b]
и T-разбиение
этого отрезка T:
a=x0<x1<…<xn<b.
Введём обозначение: Mi=sup(f(x));
m=inf(f(x))
на [xi-1;xi];
S=M1Δx1+…+MnΔxn= Свойства:
1)
Свойства
сумм Дарбу:
1)
Доказательство:
пусть
выполняется все перечисленные выше
условия, т.к. Mi=supf(x),
то по определению точной верхней грани
будет выполняться: а)
|
4.2 Следствие: если {σ(Т,ξi)} – множество всех интегральных сумм для f(x) и данного разбиения T отрезка [a;b], то s(T) = inf{σ(Т,ξi)}; S(T) = sup{ σ(Т,ξi)}; Доказательство:
а)
2)Если разбиение Т’ полученное из Т путём добавления новых точек, то S(T’)≤S(T) или S’≤S; s(T)≤s(T’) или s≤s’ Доказательство:(для верхних сумм) достаточно к разбиению Т прибавить ещё одну точку x’, [x0;x1]; S=S*+M1(x1-x0); S’=S*+ M1’(x’-x0)+ M1’’(x1-x’); S-S’= M1(x1-x0)- M1’(x’-x0)- M1’’(x1-x’)=(M1-M1’)(x’-x0)+(M1-M1’’)(x1-x’); M1’≤M; M1’’≤M’; (точная верхняя грань на части отрезка не превосходит точной верхней грани на всём отрезке). Поэтому правая часть равенства больше нуля и s-s’≥0 => s’≤s. Для нижней суммы доказательство аналогично. 3)Пусть
Т’ и T’’
-
Доказательство:
для
Следствие: множество {s} всех верхних сумм ограничено снизу любой нижней суммой, a {s} ограничено сверху любой верхней суммой. Введём
обозначение:
Определение:
числа
|
|
5. Критерий интегрируемости ограниченной функции на отрезке. Теорема:
для того,
чтобы ограниченная на отрезке функция
была интегрируема на нём, необходимо
и достаточно, чтобы
Примечание: S-верхняя, s-нижняя Доказательство: 1)Необходимость:
пусть f(x)
ограничена [a;b]
и интегрируема на нём =>
2)Достаточность:
пусть (1)
выполнено, т.к. s≤ |
6. Теорема об интегрируемости непрерывной на отрезке функции. Теорема:
непрерывная
на отрезке функция интегрируема на
нём. Введём обозначение ωi=Mi-mi-колебание
f(x)
на [xi-1;xi],
S-s= Теорема Кантора: функция, непрерывная на отрезке, равномерно непрерывна на нём. Следствие:
пусть f(x)
непрерывна на [a;b]
=>
Доказательство:
пусть f(x)
непрерывна на [a;b]
=> она равномерно непрерывна на этом
отрезке. По следствию из теоремы
Кантора:
|
|
7. Теорема об интегрируемости монотонной на отрезке функции. Теорема: монотонная на [a;b] f(x) – функция интегрируемая на [a;b]; f(a)≤f(x)≤f(b) – монотонно возрастающая. Доказательство:
пусть f(x)
– неубывающая; ε>0 разобьём [a;b]
на частные отрезки, длины которых < |
8. Свойства аддитивности и линейности определённого интеграла. Если
f(x)
интегрируема на [a;c]
и на [c;b],
то эта функция также интегрируема на
[a;b],
причём:
Доказательство:
1) a<c<b.
Т.к. f(x)
интегрируема на [a;c]
и [c;b],
что
такие разбиения этих отрезков, что
для заданного ε; S-s<ε/2
для каждого из этих отрезков (критерий
интегрируемости). Объединяя разбиения
Тi
получим [a;b]:
S-s= 2)Пусть
с 3) c<a<b (аналогично 2) ) |
|
9. Свойства определённого интеграла, выражаемые неравенствами. 1)Если
f(x)
– интегрируема на [a;b]
и f(x)≥0,
тогда
Доказательство:
т.к.
интегрируемая сумма≥ 0
Следствие:
1)если f(x)
– интегрируема на [a;b]
и f(x)≥m,
то 2)Если
f(x)
и g(x)
интегрируемы на [a;b]
и на [a;b]
f(x)≥g(x),
то
Доказательство:
поскольку
на [a;b]
f(x)≥g(x),
то
3)Если
f(x)
интегрируема на [a;b],
то |f(x)|
также интегрируема на [a;b]
и |
9.2 Доказательство: из интеграла f(x) следует интеграл |f(x)|. Пусть для [xi-1;xi]; Mi=supf(x); mi=inff(x); Mi’=sup|f(x)| и mi’=inf|f(x)|; Mi’-mi’≤Mi-mi 1)Mi и mi; Mi’-mi’= Mi + mi; 2) Mi и mi; Mi’= mi; mi’=- Mi ; Mi’-mi’< Mi - mi; 3)
mi>0;
mi<0;S-s<ε,
то
S’-s’<ε; |f(x)- интегрируема,
т.к.
-|f(x)|≤f(x)≤|f(x)|;- Замечание:
если
отказаться от ограничения a<b;a>b;то
| 4)Пусть
f(x)
и g(x)
интегрируемы на [a;b]
и g(x)≥0,
тогда если M=supf(x);
m=inff(x):m Доказательство:
|
|
10. Теорема о среднем для определенного интеграла и ее следствия. Теорема. Пусть f(x) интегрируема на [a,b] и пусть M=sup(f(x)), m=inf(f(x)). Тогда :m M, что: ab(f(x))dx=(b-a). Доказательство. При g(x)=1 на [a;b] g(x)>0: mab1dx abf(x)dx Mab(1)dx. Но поскольку ab(1)dx=(b-a), то m(b-a) ab(f(x))dx M(b-a) => m (1/(b-a))ab(f(x))dx M, т.е. =(1/(b-a))ab(f(x))dx. Следствие. Если f(x) непрерывна на отрезке [a,b], то по теореме о достижении точных граней x1[a,b] и x2[a,b], что f(x1)=sup(f(x))=M; f(x2)=inf(f(x))=m и для этих чисел [a,b], что ab(f(x))dx = f()(b-a), где f()= Обобщенная теорема о среднем. Пусть 1) f(x) и g(x) интегрируемы на [a,b]; 2) M=sup(f(x)), m=inf(f(x)); 3) g(x)0 или g(x)0 всюду на [a,b]. Тогда найдется mM такое, что ab(f(x)g(x))dx=ab(g(x))dx =f()ab(g(x))dx, где [a,b].
|
11. Теорема о непрерывности интеграла с переменным верхним пределом. Определение.
Пусть f(x)
интегрируема на [a,b],
тогда она интегрируема на любом [a,x],
где a
x
b.
Тогда
Теорема. Если f(x) непрерывна на [a,b], то F(x) = ax(f(t))dt непрерывна на этом отрезке. Доказательство. Пусть x, (x+x)[a,b], тогда F(x)=F(x+x)-F(x) = ax+x(f(t))dt - ax(f(t))dt = ax(f(t))dt+ xx+x(f(t))dt - ax(f(t))dt = xx+x(f(t))dt =(x+x-x)=x. Т.е. inf(f(x)) sup(f(x)) => lim(F(x))=lim(x) при x->0.
|
|
12. Теорема о производной интеграла с переменным верхним пределом. Существование первообразной у непрерывной на отрезке функции. Формула Ньютона-Лейбница. Теорема. Если f(x) интегрируема на [a,b] и x0[a,b], то F’(x0)=f(x0), где F(x)=ax(f(t))dt. Доказательство. Для точки x0[a,b]: lim(F(x0)/x)=f(x0) при x->0. F(x0)=F(x0+x)-F(x0). По формуле среднего значения F(x0+x)-F(x0)= x0x0+x(f(t))dt = f()x ([x0,x0+x]). Тогда x0<<x0+x и F’(x0)=f(x0). Теорема (формула Ньютона-Лейбница). Пусть f(x) непрерывна на [a,b] и пусть Ф(x) – первообразная. Тогда ab(f(x))dx=Ф(b)-Ф(a). Доказательство. По ранее доказанному F(x)=ax(f(t))dt Если F(x) и Ф(x) первообразные, то они различаются на константу С: F(x)=Ф(x)+C или ax(f(t))dt=F(x)+C. Пусть x=a, тогда 0=Ф(а)+С, С=-Ф(а) и ax(f(t))dt=Ф(x)-Ф(а). Если положить x=b, то ab(f(x))dx=Ф(b)-Ф(a).
|
13. Теорема о замене переменной в определенном интеграле. Теорема. Пусть 1) f(x) непрерывна на [a,b]; 2) x=g(t) определена на [,] так, что [a,b] – множество значений g(t); 3) g(t) имеет производную на [,]; 4) g()=a, g()=b. Тогда ab(f(x))dx=(f(g(t))*g’(t))dt – формула замены переменной в определенном интеграле. Доказательство. Пусть F(x) – первообразная для f(x). По формуле Ньютона-Лейбница ab(f(x))dx=F(b)-F(a). Т.к. функции F(x) и x=g(t) дифференцируемы на соответсвующих отрезках, то сложная функция F(g(t)) будет дифференцируемой на [,]. По правилу дифференцирования dF(g(t))/dt=F’(g(t))*g’(t) (1). Т.к. F(x) – первообразная для f(x), то F’(x)=f(x) и при x=g(t): F’(g(t))=f(g(t)). Подставляя это значение в (1), получаем d(F(g(t)))/dt=f(g(t))*g’(t). Таким образом F(g(t)) является первообразной на [,]. Тогда (f(g(t))*g’(t))dt=F(g())-F(g())=F(b)-F(a).
|
|
14. Теорема об интегрировании по частям в определенном интеграле. Теорема. Если U(x) и V(x) непрерывны на отрезке [a,b] вместе со своими производными, то abUdV=UVa|b - abVdU, где UVa|b =U(b)V(b)-U(a)V(a). Доказательство. Интеграл ab(UV)’dx = ab(U’V+UV’)dx = ab(U’V)dx + ab(UV’)dx = abVdU+ abUdV. По формуле Ньютона-Лейбница(формула Ньютона-Лейбница: Пусть f(x) непрерывна на [a,b] и пусть Ф(x) – первообразная. Тогда ab(f(x))dx=Ф(b)-Ф(a). ) abUdV=UVa|b - abVdU.
|
|
|
15. Длина дуги гладкой кривой, ее выражение в виде определенного интеграла. Определение 1. Множество {M} всех точек на плоскости OXY, координаты которых определяются уравнениями {x=(t); y=(t); t[,]; называется простой кривой L, если различным значениям t на отрезке [,] отвечают различные точки M{M}. Пусть задана кривая L и T-произвольное разбиение отрезка [,]. Обозначим M0, M1,…,Mn -соответcвующие точки кривой. Ломаную M0,…Mn назовем ломаной, вписанной в кривую L и отвечающую заданному разбиению T отрезка [,]. Обозначим li=Mi-1Mi – длину звена ломаной. Общая длина будет определятся выражением l(ti) = i=1n li. Определение 2. Кривая L называется спрямляемой, если множество {l(ti)} всех вписанных в кривую L ломаных, отвечающее всем разбиениям T отрезка [,] ограничено. Определение 3. Длиной дуги l кривой L называется Sup{l(ti)} => l>0 и существуют неспрямляемые кривые. Лемма 1. Пусть разбаению T отрезка [,] соответсвует длина длина l ломаной, вписанной в кривую L. Если разбиение T’ получено из разбиения T путем добавления новых точек, то l’l. Свойства спрямляемых кривых: 1. Если кривая спрямляема, то длина l ее дуги не зависит от параметризации этой кривой. |
15.2 2. Если спрямляемая кривая L при опмощи конечного числа точек Mi разбита на конечное число кривых Li, то каждая Li спрямляема и l= i=1n li. 3. Пусть L задана параметрическим уравнением. Обозначим через l(t) длину участка Lt, точки которого определяются всеми значениями параметра t. Тогда l(t) будет непрерывной и возрастающей функцией параметра t. Лемма 2. Пусть L задана параметрическими уравнениями{x=(t); y=(t); t[,]; и пусть при этом функции x=(t) и y=(t) имеют непрерывные производные на [,]. Тогда L – спрямляема. Доказательство. Для любого разбиения T: l(ti)=i=1n((xi - xi-1)2 + (yi - yi-1)2)1/2= i=1n(((ti)-(ti-1))2+((ti)- (ti-1))2)1/2. Т.к. x=(t) и y=(t) имеют на отрезке производные, то по формуле конечных приращений Лагранжа: (ti) - (ti-1)=’(i)(ti – ti-1)=’(i)ti и (ti) - (ti-1)=’(i*)(ti – ti-1)=’(i*)ti, где i,i*[ti-1, ti]. Отсюда получаем, что l(ti)= i=1n([’(i)]2+[’(i*)]2)1/2. Т.к. по условию функции ’(t) и ’(t) непрерывны на [,], о они ограничены на этом отрезке, что и означает, что кривая спрямляема. Теорема. При условии Леммы 2 длина дуги кривой определяется как l=(([’(t)]2+[’(t)]2)1/2)dt. Другие случаи выражения длины дуги кривой:
Функция полярных координат r=r(). L:{x=Rcos; y=Rsin; l=12(([R()]2+[R’()]2)1/2)d. |
|
16. Понятие площади плоской квадрируемой фигуры. Теорема о квадрируемости криволинейной трапеции. Определение 1. Говорят, что многоугольник вписан в фигуру Q, если каждая его точка принадлежит Q. Многоугольник описан вокруг Q если любая точка фигуры принадлежит многоугольнику. Пусть дана фигура Q с замкнутой границей L. Обозначим через {Sв}множество площадей всех вписанных многоугольников в эту фигуру, а через {So} множество всех описанных многоугольников. Обозначим через P=Sup{Sв}и P’=inf{So}. P’ и P называются соответственно верхней и нижней площадью фигуры Q. Определение 2. Фигура Q называется квадрируемой, если P=P’, при этом p=P=P’ – площадь фигуры Q. Теорема 1. Для того что бы Q была квадрируемой необходимо и достаточно что бы >0 So, Sв: (So-Sв)<. В этом случае граница Q имеет площадь равную 0. Теорема 2. Криволинейная трапеция квадрируема. Ее площадь вычисляется как p= ab(f(x))dx. Доказательство. Т.к. в следствии непрерывности f(x) на [a,b] она интегрируема на этом отрезке, т.е >0 T, что для верхних и нижних сумм Дарбу: (S-s)<. Но S=So, s=Sв, что и означает, что криволинейная трапеция – квадрируемая фигура. Кроме того lim(s)=lim(S)=ab(f(x))dx при t->0 и s p S => p= ab(f(x))dx. Док-во для теоремы 1: |
17. Определение несобственных интегралов по бесконечному промежутку и от неограниченных функций. Критерий Коши сходимости несобственного интеграла. Несобственный интеграл 1 рода (интеграл для неограниченного промежутка интегрирования). Будем рассматривать прямую и полупрямую.
Определение 1. Предел функции (1) при B->+ называется несобственным интегралом 1 рода. Если предел существует, то интеграл называется сходящимся, в противном случае – расходящимся. Несобственный интеграл 2 рода (интеграл от неограниченных функций). Пусть на [a,b) задана f(x). Определение 2. Число b называется особой точкой, если f(x) не ограничена на [a,b), но ограничена на любом [a,b-)[a,b), где >0 и a<b-. Будем предполагать, что на любом a<b- функция f(x) интегрируема, т.е. задана функция аргумента : F()=ab- (f(x))dx (2). Определение 3. Предел функции (2) при ->+0 называется несобственным интегралом 2 рода. Если предел существует, то интеграл называется сходящимся, в противном случае – расходящимся. Понятие несобственного интеграла можно распространить на конечное число особых точек. Теорема (Критерий Коши). Для сходимости несобственного интеграла 1 рода необходимо и достаточно, что бы >0 A()>0: B’> A и B’’> A: |b’b’’(f(x))dx|<. Для сходимости несобственного интеграла 2 рода необходимо и достаточно что бы >0 ()>0: ’> и ’’>: |b-’b-’’(f(x))dx|<. Доказательство. о сходимости несобственного интеграла 1 и 2 рода сводится к у о существовании предела соответствующей функции. |
|
18. Абсолютная и условная сходимость несобственного интеграла по абсолютному промежутку. Признак абсолютной сходимости, основанный на сравнении подинтегральных функций. Пусть f(x) интегрируема [a,b], тогда |f(x)| так же интегрируема на этом отрезке. Определение 1. Несобственный интеграл a+(f(x))dx называется абсолютно сходящимся, если a+(|f(x)|)dx сходится. Определение 2. Несобственный интеграл a+(f(x))dx называтся сходящимся условно, если он сходится, а a+(|f(x)|)dx расходится. Теорема. Из абсолютной сходимости интеграла следует просто его сходимость. Доказательство. Пусть a+(f(x))dx сходится, тогда по критерию Коши |b’b’’(|f(x)|)dx|< =>|b’b’’(f(x))dx||b’b’’(|f(x)|)dx|<. Теорема (признак Абеля-Дирехле). Пусть 1) p(x), g(x) определены на [a, +); 2) функция f(x) непрерывна на этой полупрямой и имеет ограниченную первообразную F(x); 3) g(x) монотонной убывает и g(x)->0 при x->+; 4) g(x) имеет g’(x) (непрерывную). Тогда a+(f(x)g(x))dx сходится. Доказательство: без доказательства |
19. Теоремы о замене переменной и об интегрировании по частям в несобственных интегралах. Теорема 1 (замена переменной). Пусть: 1) f(x) непрерывна на [а; +). 2) [а; +) - множество значений строго монотонной x = g (t). 3) g (t) задана на [; +[. 4) g (t) дифференцируема на этой полупрямой. 5) g()=a. Тогда из сходимости одного из интегралов а+f(x)dx; +f(g(t))g’(t)dt cледует сходимость другого и равенство этих интегралов. Доказательство. Рассмотрим произвольный отрезок [a,b] ему (в силу строгой монотонности g(t)) отвечает некоторый отрезок [,], такой что при изменении t на [,] значения функции х = g(t) заполняют весь [a,b], причем g() = b; т. е. выполнены все условия для теоремы о замены переменной для определенного интеграла на отрезке. Поэтому: а+f(x)dx = +f(g(t))g’(t)dt, при x = g(t). В-> при ->. Теорема 2 (интегрирование по частям). Пусть: 1) U(x) и V(x) имеют непрерывные производные на полупрямой [а; +). 2) Существует lim U(x)V(x) = A, при х-> +. Тогда из сходимости одного из интегралов: а+UdV или а+VdU, следует сходимость другого, причем а+UdV= А – U(a)V(a) - а+VdU. Доказательство. На произвольном отрезке [a,B] действует обычная формула интегрирования по частям: а+UdV = UVa|B - а+VdU. При В-> +: UVa|B ->А - U(a)V(a) => одновременная сходимость или расходимость указанных интегралов и справедливость формулы доказана.
|
|
20. Определение многомерности координатного евклидова пространства. Неравенство Коши-Буняковского. Неравенство треугольника. Определение 1. Метрическим пространством R называется пара (Х,), где Х – заданное множество, - действительная функция, определенная для любых двух элементов множеста Х и удовлетворяющая условиям: 1) (х,у) 0 х,уХ. 2) (х,у) = 0 <=> х=у. 3) (х,у) = (у,х). 4) (х,z) (х,у) + (y,z) – неравенство треугольника. - метрика метрического пространства R. R=(X,). (х,у) – расстояние между х и у. Определение 2. Координатным n-мерным пространством Kn называется множество упорядоченных совокупностей (х1,…,хn) n чисел. Всякий элемент можно представить как набор этих чисел: у = (у1,…,уn). Определение 3. Координатное n-мерное пространство En называется евклидовым, если для любых двух точек En введена метрика (х,у) по формуле: (х,у)= ((х1-у1)2+…+(хn-уn)2)1/2. Лемма (неравенство Коши-Буняковского). Для двух вещественных чисел ai, bi (i=1,…,n) справедливо
|
21. Предел последовательности точек в многомерном евклидовом пространстве. Критерий Коши сходимости последовательности точек. Определение 1. Пусть каждому натуральному kN ставится в соответсвие хkЕn, тогда упорядоченное множество {xk} называется последовательностью точек этого пространства. Определение 2. Последовательность {xk} называется сходящейся, если х0En >0 N() kN => (xk,x0) < . Точка х0 – предел последовательности {xk}. Определение 3. Последовательность точек {xk} пространства En называется фундаментальной, если >0 N() kN и натурального p => (xk+p,xk) < . Замечание. Из фундаментальности {xk} следует фундаментальность последовательности координат {xik}. Т. к. i: |xik+p – xik| (xk+p,xk) < . Верно и обратное: (xk+p,xk) =( i=1n( xik+p – xik)2)1/2 (n*max|xik+p – xik |)1/2 < n1/2*/n1/2 = . Теорема (критерий Коши). Для того чтобы последовательность {xk}En была сходящейся, необходимо
|
|
22. Теорема о связи поточечной и покоординатной сходимости. Теорема. Для того чтобы последовательность {xk} = {(xk1,…,xkn)} сходилась к х0 = (х10,…,хn0) необходимо и достаточно, чтобы i => lim(xik)=xi0, k-> (i=1,…,n). Поточечная сходимость <=> покоординатная сходимость. Доказательство. 1) Необходимость. Пусть lim(xk)=xo, k->. Зафиксируем >0 N() kN: (xk,x0)<. По координатам: ((x1k-x10)2+…+(xnk-xn0)2)1/2 < => |x1k-x10| < ,…,|xnk - xn0| < . Lim(x1k)=x10,…, lim(xnk)=xn0, k->. 2) Достаточность. Пусть последовательности координат сходятся соответственно к числам х10,…,хn0, тогда >0 N1,…,Nn kN1,…, kNn => |x1k – x10|</n1/2,…, |xnk – xn0|</n1/2. Пусть N = max(N1,…,Nn), тогда kN => ((x1k-x10)2+…+(xnk-xn0)2)1/2 < (n2/n)1/2 = => (xk,x0)<. Теорема доказана. Замечание. Из этой теоремы, а также из свойств пределов числовых последовательностей следует, если последовательность точек имеет предел, то он единственный. Всякая подпоследовательность точек данной последовательности сходится к тому же пределу. Все свойства, связанные с пределом числовых последовательностей, относятся и к точкам.
|
23. Предел функции многих переменных в точке (по совокупности переменных). Теорема о повторном пределе. Пусть f(x) задана на X и пусть х0 = (х10,…,хn0). Определение. Число b называется пределом функции f(x) в точке x0, если: (Гейне) {xk}->x0 => {f(xk)}b; (Коши) >0 ()>0 xX: 0<(x,x0)< => |f(x)-b|<. Арифметические операции над функциями, имеющими предел:
Повторный предел. Предел по одной из переменных получим, зафиксировав (как параметр) остальные. lim(f(x1,…,xn))=(x2,…,xn), x1->x10,
|
|
24. Непрерывность функции многих переменных в точке и на множестве. Теорема о непрерывности сложной функции. Определение 1. Функция f(x) называется непрерывной в точке А, если предел этой функции в x0 существует и равен частному значению f(x0). Определение 2. U=f(x) непрерывна в х=(х1,…,хn) по переменной хi, если limxiU=0, xi->0. Определение 3. (Гейне не нужен)U=f(M) непрерывна в А, если: (Гейне) {Mn}->A => {f(Mn)}-> f(A); (Коши) >0 ()>0 x{X}: (x,x0)< => |f(x)-f(x0)|<. Основные свойства непрерывных функций: если f(x) и g(x) непрерывны, то непрерывны и функции f(x)g(x), f(x)g(x), f(x)/g(x), Cf(x), C=const Сложная функция. Функции x1=1(t1,…,tk),…, xm=m(t1,…,tk) заданы на множестве {N}Ek. Тогда N{N} MEm. {M} – множество всех таких точек. u=(x1,..,xm) – сложная функция. Теорема. Пусть x1=1(t1,…,tk),…, xm=m(t1,…,tk) непрерывны в А(а1,…,аk), а u=f(x1,..,xm) непрерывна в
|
25. Теорема о промежуточных значениях непрерывной функции. Теорема. Пусть: 1) u=f(x) непрерывна на ХEn. 2) f(А) и f(В) – значения этой функции в т. А,ВХ. 3) С – любое промежуточное значение между f(А) и f(В). Тогда на любой непрерывной кривой L (LX), соединяющей А и В N: f(N)=C. Доказательство. Пусть непрерывная кривая, соединяющая А и В задана уравнением: L: {x1=1(t),…, xn=n(t), или x=(t), t. На [,] определена сложная функция u=f(x) =f((t)). Значения этой функции на [,] совпадают со значениями u=f(x). Сложная функция (по теореме о непрерывности сложной функции) будет непрерывна на [,], причем она является функцией одной переменной t, согласно соответствующей теореме для функции одной переменной [,]: f(x)= f(1(),…,n())=С. Поэтому в NL с координатами N=(1(),…,n()): f(N)=C.
|
|
20. неравенство: |i=1n(aibi)| ( i=1n (ai)2)1/2*( i=1n (bi)2) 1/2 (1). Доказательство. Для i: ai=0 неравенство очевидно. Пусть i=1nai 0. F(t)= i=1n(ai*t+bi)2= t2i=1n(ai)2 + 2t*i=1n(aibi) + i=1n(bi)2 (2). F(t) 0 => (2) либо не имеет вещественных корней, либо имеет два одинаковых корня, значит D0. (i=1n(aibi))2 - i=1n(ai)2 * i=1n(bi)2i 0 => (1). Следствие. (i=1n(ai+bi))1/2 (i=1n(ai)2)1/2 + (i=1n(bi)2)1/2 (3). Доказательство. (i=1n(ai+bi))1/2= i=1n (ai)2 + 2* i=1n(aibi) + i=1n (bi)2 i=1n (ai)2 + 2(i=1n (ai)2)1/2*(i=1n (bi)2)1/2 + i=1n (bi)2 = ((i=1n(ai)2)1/2 + (i=1n (bi)2)1/2)2 => (3). Теорема. В евклидовом пространстве справедливо неравенство треугольника. Доказательство. Пусть х=(х1,…,хn), y=(y1,…,yn), z=(z1,…,zn) – произвольные точки En. ai=xi-yi, bi=yi-zi, ai+bi= xi-zi. Согласно (3): (i=1n( xi-zi))1/2 ( i=1n ( xi-уi))1/2 + (i=1n( уi-zi))1/2. Т. е. (x,z) (x,y)+(y,z). Таким образом, евклидово пространство метрическое, с метрикой (х,у)= ((х1-у1)2+…+(хn-уn)2)1/2. |
21. и достаточно, чтобы она была фундаментальной. Доказательство. 1) Необходимость сразу следует из предыдущего замечания. Действительно, если {xk} сходится, то сходятся и все последовательности координат {xik}. Поэтому эти последовательности координат фундаментальны. Из замечания следует, что последовательность точек фундаментальна. 2) Достаточность. Пусть {xk} – фундаментальна, тогда фундаментальны все последовательности координат {xik} => все последоватеьности координат сходятся => сходиться {xk}. |
|
23. lim(f(x2,…,xn))=(x3,…,xn), x2->x20,…, и. т. д. lim(lim(f(x1,…,xn)))= (x3,…,xn), x2->x20, x1->x10. Замечание. В конце можем получить число, не обязательно равное limf(x1,…,xn)= b, x1->x01,…, xn->xn0. Теорема. Пусть f(x,у) определена в прямоугольной окрестности точки М0(х0,у0) |x-x0|<d1, |y-y0|<d2 и имеет в М0 предел lim(f(x,y))=b, x->x0, y->y0. И пусть существуют lim(f(x,y))=(y), x->x0 и lim(f(x,y))=(y), y->y0. Тогда выполняется: lim((y))[y->y0]=lim(lim(f(x,y)))[y->y0] [x->x0]=lim(x)[x->x0]=lim(lim(f(x,y)))[x->x0][y->y0]=b. Доказательство. Т. к. f(x,у) имеет предел в М0(х0,у0): >0 ()>0 x,y: |x-x0|<, |y-y0|< => |f(x,y)-b|<. Таким образом, в прямоугольной окрестности М0 значение f(x,y) отличается от b не более чем на . Но тогда пределы (х) и (у) при х и у, удовлетворяющих неравенствам |x-x0|<, |y-y0|<, также отличаются от b не более чем на . Следовательно, и пределы этих функций в х0 и у0 соответственно существуют и равны b. |
24. В(b1,…,bm), где bi=i(a1,…,ak), i=1,…,m. Тогда сложная функция u=f(x1,..,xm), где x1,..,xm – функции от t1,…,tk, непрерывна в А(а1,…,аk). Доказательство. Рассмотрим произвольную сходящуюся к А последовательность точек Nn={(t1n,…,tkn)} множества {N}. {Mn} – соответствующая последовательность точек пространства Em, координаты которых xin=i(N)= i(t1n,…,tkn), i=1,…,m. Из непрерывности i(N) в А и из определения непрерывности по Гейне вытекает сходимость последовательности точек {Mn} к точке B(b1,…,bm). Далее из непрерывности функции u=f(М) в точке В и из определения непрерывности по Гейне вытекает сходимость {f(Mn)}->f(B). Это и означает, что последовательность f[1(Nn),…, m(Nn)] значений этой сложной функции сходится к частному значению этой сложной функции f[1(А),…, m(А)], т. е. непрерывность сложной функции в точке А. |
|
26. Ограниченность функции многих переменных, непрерывной на ограниченном замкнутом множестве. Теорема. Если u=f(M) непрерывна на замкнутом, ограниченном множестве {M}, то она ограничена на нем. Доказательство. Предположим, что она не ограничена на М. Выделим последовательность {Mn}, для которой |f(Mn)|>n Последовательность функций ограничена. По теореме Больцано-Вейерштрасса, из любой ограниченной последовательности можно выделить {MNk}M0, т. к. {М} замкнуто, то М0{M}. Очевидно, что последовательность {f(MNk)} бесконечно большая. С другой стороны, в силу непрерывности функции в точке М эта последовательность должна сходится к f(М). Противоречие доказывает теорему.
|
27. Теорема об устойчивости знака непрерывной функции. Теорема. Если u=f(x) непрерывна в х0Х (множество определения функции) и f(x0)0, то найдется -окрестность точки х0, в которой f(x) имеет знак, совпадающий со знаком f(x0). Доказательство. Пусть f(x0)>0, тогда (вследствие непрерывности f(x) в х0) >0 ()>0 x: (x,x0)< => |f(x)-f(x0)|<. Пусть =f(x0). f(x0)-< f(x)< f(x0) +. f(x)>f(x0) - f(x0)=0. f(x)>0 при (х,х0)<. Если f(х0)<0, тогда = -f(x0).
|
|
28. Равномерная непрерывность функции многих переменных на ограниченном замкнутом множестве. Определение 1. f(x) называется равномерно непрерывной на {Х} n, если х' и х” : х',х” |f(x’) – f(x”)| . Из равномерной непрерывности f на множестве Х следует непрерывность f на этом множестве. Теорема (Кантора о равномерной непрерывности). Непрерывная на замкнутом ограниченном множестве f(x) равномерно непрерывна на этом множестве. Доказательство. Аналогично функции одной переменной. [a; b] ; x->x; |x’-x”|->x’,x”; Предположим, что непрерывная на Х функция не является равномерно непрерывной и x’X и x”X : х',х” |f(x’) – f(x”)|, т.к. {xn’} является ограниченной, то по теореме Больцано-Вейерштрасса, из нее можно извлечь подпоследовательность {xnk’}, сходящуюся к некоторой точке сХ. Из неравенства хn',хn” , где =1/n->0, следует, что к точке с будет сходиться подпоследовательность {xnk”} последовательности {xn”}, т.к. расстояние между ними меньше любого числа. Т.к. f(x)
|
28.2 непрерывна в точке с, то пределы последовательностей {f(xnk’)} и {f(xnk")} будут равны f(c), это означает, что {f(xn1’)}-{f(xn2”)} является бесконечно малой последовательностью. Но по нашемы предположению этого быть не может, т.к. |f(x’) – f(x”)| Определение 2. Диаметром d связного множества Х называется число d=sup((x’,x”)) Следствие (из теоремы Кантора). Пусть f(x) непрерывна на ограниченном замкнутом множестве Х. Тогда , что на *Х, для которых : d, колебания f(x) [supf(x)-inff(x)] Доказательство. Аналогично функции одной переменной. По теореме Кантора. |
|
29. Дифференцируемость и полный дифференциал функции многих переменных. Необходимое и достаточное условие полной дифференцируемости. Опр-е. Функция u=f(x1,..,xn) называется дифференцируемой в точке x=(x1,...,xn), если ее полное приращение u=f(x1+x1,...,xn+xn) - f(x1,...,xn) в это точке может быть представлен в виде u=А1x1+…+Аnxn+x1+…+nxn (2), где A1,...,An=const, i=i(x1,...,xn) – бесконечно малая при (x1,…,xn)->0, т.е. i : lim(i(x1,..,xn))=0 при (x1,…,xn)->0. Причем при (x1,…,xn)=0 будем полагать (1,...,n)=0. Другие формы условия дифференцируемости (2): Пусть =(x+x, x) – расстоянию между х и х+х. Т.е. =(x12 +…+ xn2)1/2. Очевидно, что lim=0 при (x1,…,xn)->0. |x1+…+nxn| = |x1/+…+nxn/| (|1|*|x1|/+…+|n|*|xn|/) (|1|+…+|n|)=o() при ->. Таким образом, условие дифференцируемости может быть записано следующим образом: u=А1x1+…+Аnxn + o() (3), где -> при х->. и при этом условии считать, что o()=0 при =0. Условия (2) и (3) эквивалентны |
29.2 Замечание: Если хотя бы одно из чисел А1,…,Аn 0, то А1x1+…+Аnxn – главная линейная часть приращения функции f в точке х относительно приращения аргументов. Если же i : Ai=0, то мы также будем считать функцию дифференцируемой. Теорема (необходимое условия дифференцируемости). Если U=f(x1,...,xn) дифференцируема в точке x=(x1,...,xn), то в этой точке существует произведение по всем аргументам. Причем U/x1=A1,...,U/xn=An, где A1,...,An определены из условия (2) или (3) дифференцируемости функции. Доказательство. Пусть f(x) дифференцируема в точке x, т.е. выполняется условие (2). Рассмотрим частное приращение x1U функции в этой точке: x1U =A1х1+1х1 (остальные xi=0). Рассмотрим x1U/x1=A1+1(x1), lim(1(x1))=0 при х1->0, если рассмотрим lim(x1U/x1)=U/x1=A1. Аналогично доказывается, что i : U/xi=Ai След1. Условие дифференцруемости U=f(x) в x может быть записано в виде: u=(U/x1)x1+…+(U/xn)xn+o() (4)
|
|
29.3 След2. Если U=f(x) дифференцируема в х, то представление полного приращения U в форме (2) или (3) единственно. Док-ство: Коэффициенты Ai – частные производные, т.е. пределы. Но раз они существуют, то единственны. Теорема (достаточ условие дифференцируемости). Если U=f(x) имеет частную производную по всем аргументам в точке х0, и эти частные производные непрерывны в самой точке х0, то f будет дифференцируема в точке х0. Док-во. Рассмотрим u=f(x,y). Пусть в окрестности точки М0(x0,y0) и в самой этой точке существует и непрерывна частная производная fx’ и fy’. Пусть x и y таковы, что точка (x0+x,y0+y) не выходят за пределы заданной окрест-ти точки М0. Запишем полное приращение функции в точке М0 u=f(x0+x, y0+y)-f(x0,y0)=[f(x0+x, y0+y) - f(x0, y0+y)]+[f(x0, y0+y) - f(x0,y0)]. Рассмотрим первую скобку: это приращение функции только одной переменной f(x0, y0+y) на [x0,x0+x], т.к. u=f(x,y) имеет частную производную, то f(x0, y0+y) диф-ма и ее производная по Х – функция одной переменной – частная производная fx’.
|
29.4 Применяем формулу конечных приращений Лагранжа: [f(x0+x, y0+y)-f(x0, y0+y)]=fx’(x0+1x, y0+y)x, 0<1<1. Аналогично для второй скобки получим: [f(x0, y0+y)-f(x0, y0)]=fy’(x0, y0+2y)y, 0<2<1. Т.к. по условию теоремы, fx’ и fy’ непрерывны в М0, то мы можем представить fx’(x0+1x, y0+y)=fx’(x0,y0)+; fy’(x0, y0+2y)= fy’(x0,y0)+. Lim(x, y)=lim(x,y)=0 при x, y->0 u=[fx’(x0, y0)+]x + [fy’(x0,y0)+]y=fx’(x0,y0)x+fy’(x0,y0)y => непрерывна, а следовательно, дифференцируема. Определение. Пусть u=f(x) дифференцируема в х0. Дифференциалом du функции f(x) в х0 называется главная линейная часть приращения функции относительно приращения аргумента в точке х0. Т.е. du=А1x1+…+Аnxn (5) Если A1=…=An=0, то по определению du=0. По ранее доказанному: du=(u/x1)x1+…+(u/xn)xn (6) Под дифференциалом dxi независимой переменной xi будем понимать любое число, независимое от x1,…,xn (либо приращение аргумента в этой точке) dxi=xi => du=(u/x1)dx1+…+(u/xn)dxn (7) |
|
30. Теорема о дифференцируемости сложной функции, вычисление частных производных. Инвариантность формы первого дифференциала. Пусть дана сложная функция u=f(x1,..,xn), где x1=1(t1,…,tn)…xn=n(t1,…,tn) (1). Покажем, что при определенных условиях эта сложная функция является дифференцируемой по t1,…,tk. Причем, частные производные выражаются следующим образом: u/t1=(u/x1)(x1/t1)+…+(u/xn)(xn/t1);…;u/tk=(u/x1)(x1/tk)+…+(u/xn)(xn/t1) (2) или u/ts = i=1n(u/xi)(xi/ts) (2’) Теорема. Пусть функции (1) дифференцируемы в некоторой точке t0=(t10,...,tk0). Пусть u=f(x1,..,xn) дифференцируема в соответствующей точке x0=(x10,...,xk0), где xi0=i(t10,...,tk0) (i=1,..,n). Тогда сложная функция u=f(x1,...,xn), где xi, определенная функциями (1), дифференцируема в точке t0. Частная производная сложной функции в точке t0 определена функциями (2), где частная производная u/xi берутся в х0, а частная производная xi/ts берутся в t0. дифференцируема в x0, то это приращение может быть записано в виде u=(u/x1)x1+…+(u/xn)xn+x1+…+nxn (3), где 1,...,n – бесконечно малые при (x1,…,xn)->. причем i(0)=0. Т.к. по условию теоремы функции (1) дифференцируемы в t0, то i : xi=(xi/t1)t1+…+(xi/tk)tk + o (4), где xi/tk берутся в точке t0, а =(t12+…+tk2)1/2. Подставим (4) в правую часть (3). Рассмотрим первое слагаемое суммы (3). согласно формуле (4), (u/x1)x1+x1=(u/x1)((xi/t1)t1+…+(xi/tk)tk)+(u/x1)o()+1x1. Рассмотрим 1) u/x1 в х0 есть const => (u/x1)o()=o(); 2) x1-> при t10, т.е. при . Поэтому 1x1 = o(). Таким образом |
30.2 (u/x1)x1+x1=(u/x1)(xi/t1)t1+…+(u/x1)(xi/tk)tk+o(). Эти же рассуждения применимы и для других слагаемых. Группируя все слагаемые (3), после подстановки (4) по приращению ts, получим u=((u/x1)(x1/t1)+…+(u/xn)(xn/t1))t1+…+((u/x1)(x1/tk)+…+(u/xn)(xn/t1))tk+(o()+…+o()) =>u=А1 t 1+…+Аn t n+o(), где A1,..,An=const. As=(u/x1)(x1/ts)+…+(u/xn)(xn/ts) (s=1,..,k). Теорема: Пусть дана u=f(x1,...,xn), аргументы которой xi=i(t1,...,tn) также дифференцируемые функции. Тогда первый дифференциал функции u=f(x1,...,xn) имеет тот же вид, что и дифференциал этой функции для независимой переменной: du=(u/x1)dx1+…+(u/xn)dxn. Доказательство: Функция u=f(x1,...,xn) – сложная функция от аргументов t1,..,tk. Поэтому дифференциал можно представить в виде du=(u/t1)dt1+…+(u/tk)dtk (1), {u/t1=(u/x1)(x1/t1)+…+ (u/xn)(xn/t1);..; u/tk=(u/x1)(x1/tk)+…+ (u/xn)(xn/tk) (2). Подставив (2) в (1) и сгруппировав получим: du=(u/x1)((x1/t1)dt1+…+ (x1/tk)dtk)+…+ (u/xn)((xn/t1)dt1+…+ (xn/tk)dtk)= (u/x1)dx1+…+ (u/xn)dxn Частная производная – это обычная производная по какому- либо аргументу при фиксированных остальных аргументах. Поэтому вычисление частных производных происходит по известным законам дифференцирования функции одной переменной. |
|
31. Касательная плоскость и нормаль к гладкой поверхности. Геометрический смысл частных производных и полного дифференциала функции многих переменных. Пусть функция z=f(x,y) дифференцируема в точке М0(x0,y0). Рассмотрим на поверхности, определенной этой функцией, точку N0(x0, y0, z0), где z0=f(x0,y0). Пусть A(x-x0)+B(y-y0)+C(z-z0)=0 (1) – некоторая плоскость, проходящая через точку N0 и непараллельная 0Z. Тогда, положив C=-1, можем уравнение плоскости записать в виде: z=z0+A(x-x0)+B(y-y0) (2). Опр-е. Касательной плоскостью к графику функции f(x,y) в точке N0 называется такая плоскость, для которой в точке N0 справедливо соотношение: f(x,y)-z=o() (3), где z – аппликата плоскости, а =((x-x0)2+(y-y0)2)1/2 ->0 при x->x0, y->y0. Найдем уравнение этой касательной плоскости. Т.к. f дифференцируема в М0, то z=f(x,y)-f(x0,y0)=fx’(x0,y0)x+fy’(x0,y0)y+o() или f(x,y)=z0+fx’(x0,y0)(x-x0)+fy’(x0,y0)(y-y0)+o() (4). Вычитаем
|
31.2 (2) из (4): f(x,y)-z=(A-fx’(x0,y0))(x-x0)+(B-fy’(x0,y0))(y-y0)+o(). Чтобы получить условие (3): A=fx’(x0,y0), B=fy’(x0,y0). Такм образом уравнение касательной плоскости запишется в виде fx’(x0,y0)(x-x0)+fy’(x0,y0)(y-y0)-(z-z0)=0 (5) Опр-е. Нормалью к поверхности в точке N0 называется прямая, проходящая через эту точку перпендикулярно касательной плоскости. Согласно соотношению (5): (x-x0)/fx’(x0,y0)=(y-y0)/fy’(x0,y0)=(z-z0)/(-1) (6) Опр-е. Поверхность z=f(x,y) называется гладкой, если она в каждой своей точке имеет касательную плоскость, т.е. f(x,y) – диффер-ема в любой точке своей области определения. Геометрический смысл полного дифференциала. Уравнение касательной плоскости (5) в точке N0 можно представить в виде dz-(z-z0)=0; dz=(z-z0) => Полный дифференциал функции f(x,y) в точке М0 (точке области определения) равен приращению аппликаты плоскости касательной к графику функции. Геометрический смысл частных производных: Рассмотрим функцию двух переменных: u=f(x,y). f(x0,y0)/x=tg; f(x0,y0)/y=tg. N{x0,y0,f(x0,y0)} |
|
32. Производная по направлению и градиент функции многих переменных. Выражение произвдн через градиент. Пусть f(x) задена в некоторой окрестности точки x0 пространства En. Пусть прямая x=x0+lt (1), |l|=1 проходит через x0. Вдоль этой прямой функция F становится функцией одной переменной: f(x)=f(x0+lt)=f(x0+l1t,...,x0+lnt). Определение. Если функция f(x0+lt) дифференцируема по t в точке t=0, то говорят, что эта функция дифференцируема в x0 по направлению l. Производная обозначается f/l Определение. Выражение (u/x)cos+(u/y)cos+(u/z)cos можно представить как: u/l={u/x,u/y,u/z}{cos,cos,cos} (5). Градиентом u=f(x,y,z) в M0 называется вектор (5). Grad(U)={u/x,u/y,u/z}|M=M0. GradU=(u/x)i+(u/y)j+(u/z)k. u/l=grad(l0), l0=l/|l|; u/l=|l0|ПРlgradu= ПРlgradu. Замечание: Введем оператор Набла (оператор Гамильтона): =(/x)i+(/y)j+(/z)k; gradU=U=(u/x)i+(u/y)j+(u/z)k
|
33.Частные производные и дифференциалы высших порядков. Теорема о независимости частных производных от порядка дифференцирования. Пусть дана функция u=f(x1,..,xn), определенная в области Х. Пусть частная производная u/xi существует в Х, тогда она равна (x1,...,xn). Пусть теперь u/xi имеет частную производную по xk, тогда (/xk)(u/xi) называется второй частной производной сначала по xi , затем по xk. При этом пишут: (/xk)(u/xi)=(2u/xkxi)=fXiXk”=uXiXk”. Если ik, то такая производная называется смешанной производной второго порядка. Аналогично вводится производная любого n-ого порядка. Опр-е. Частной производной от частной производной (n-1) порядка называется частная производная N-ого порядка. При этом под производной нулевого порядка будем понимать саму функцию. Частные производные по различным аргументам также называются смешанными производными. Теор (о смешанной производной). Пусть f(x,y) определена вместе со своими частными производными fx’,fy’,fxy” ,fyx ” в некоторой окрестности М0(x0,y0). Причем производные fxy” и fyx” непрерывны в этой точке. Тогда fxy” =fyx” Док-во. Рассмотрим выражение w=[[f(x0+h, y0+k)-f(x0+h, y0)]-[f(x0, y0+k)-f(x0,y0)]]/(h*k), h,k0, (x0+h,y0+k)U(M0(x0,y0)). Введем вспомогательную функцию (х)=[f(x, y0+k)-f(x,y0)]/k, которая, согласно условиям теоремы, имеет производную на (x0,x0+h). Найдем производную ’(х)=[fx’(x, y0+k)-fx’(x,y0)]/k и она является непрерывной. С помощью этой функции: =1/h[[f(x0+h, y0+k)-f(x0+h, . y0)]-[f(x0, y0+k)-f(x0,y0)]]/k=1/h[(х0+h) - (х0)]. Т.к. эта функция |
|
33.2 дифференцируема и непрерывна, применим формулу конечных приращений Лагранжа на [x0,x0+h]: =(1/h)’(x0+1h)h=’(x0+1h)=[fx’(x0+1h,y0+k)-fx’(x0+1h,y0)]/k. К этой функции применим формулу Лагранжа на [y0,y0+k]: =fxy”(x0+1h, y0+2k)k/k=fxy”(x0+1h,y0+2k), 0<1<1,0<2<1. Аналогичным образом введем (y)=[f(x0+h,y)-f(x0,y)]/h, которая дифференцируема и непрерывна на [y0, y0+k]. =fyx”(x0+3h,y0+4k), 0<3<1, 0<4<1 => fxy”(x0+1h, y0+2k)=fyx”(x0+3h,y0+4k). Из определения смешанной производной следует, что при h->0, k->0 fxy”(x0,y0)=fyx”(x0,y0). Замеч. Из этой теоремы по индукции можно доказать следующее: если f(x,y) определена в окрестности M0(x0,y0) вместе со своими производными до n-ого порядка включительно, причем смешанная производная n-ого порядка непрерывна, то значение любой n-ой производной не зависит от того порядка, в котором производная диф-ма. Замечание. Аналогично теорема переводится на функции многих переменных. Док-во. f(x1,...,xn, y1,...,yn)=i=k=1naikxiyk будем называть билинейной формой от переменных x1,...,xn, y1,...,yn. Квадратичной формой будем называть функцию f(x1,..,xn,x1,..,xn)=i=k=1naikxixk. Если aik=aki, то билинейные и квадратичные формы называются симметричными. Для обозначения дифференциалов: d, ; du=(u/x)dx+(u/y)dy, u=(u/x)x+(u/y)y. Пусть u=f(x,y) определена на некотором открытом множестве G и принадлежит классу С2. Тогда в любой точке {G} определен первый дифференциал du=(u/x)dx+(u/y)dy (1). Заметим, что u/x и u/y – функции независимых переменных x,y; dx,dy=const; du – непрерывна и дифференцируема. Второй дифференциал: (du)=((u/x)dx+(u/y)dy)=(u/x)dx+(u/y)dy=((2u/x2)x+(2u/xy)y)dx+((2u/yx)x+(2u/y2)y)dy=((2u/x2)x)dx+((2u/xy)y)dx+((2u/yx)x)dy+((2u/y2)y)dy=f(x,y,dx.dy) (2) – симметричная билинейная форма от x,y,dx.dy, т.к. 2u/xy=2u/yx Опр-е. Квадратичная форма, соответствующая билинейной форме (2), называется вторым дифференциалом функции u=f(x,y) и обозначается d2u=(2u/x2)dx2+2(2u/xy)dxdy+(2u/y2)dy. Аналогично вводится понятие третьего дифференциала d3u=(d2u); x=dx, y=dy |
34. Формула Тейлора для функции многих переменных с остаточных членом в форме Лагранжа. Теорема. Пусть U=f(M)=f(x1,...,xn) определена в некоторой -окрестности точки M0(x10,..,xn0) и пусть эта функция (n+1) раз дифференцируема в этой окрестности. Тогда полное приращение этой функции в точке М0 U=f(M)-f(M0), где МО(,М0) может быть представлена в виде U=df(M0)+(1/2!)d2f(M0)+…+(1/n!)dnf(M0)+(1/(n+1)!)dn+1f(N), где N – некоторая точка О(,М0) (1) Отметим, что (1) – формула Тейлора функции f с остаточным членом в форме Лагранжа: f(M)=f(M0)+k=1n[(dkU(M0))/k!]+[(dn+1U(N))/(n+1)!] Доказательство. (U=f(x,y)). U=F(t) – функция одной переменной, которая (n+1) раз дифференцируема в некоторой окрестности t0. Напишем формулу Тейлора для этой функции с остаточным членом в форме Лагранжа: F(t)-F(t0)=k=1n[(F(k)(t0)/k!)(t-t0)k]+(1/(n+1)!)F(n+1)(t0+(t-t0))(t-t0)n+1 (2), 0<<1, t – независимая переменная; t=t-t0=dt, т.е. дифференцируема в точке t0 => F(k)(t0)(t-t0)k=F(k)(t0)dt2=dkF(t0)= dkU(t0). Кроме того, F(t)-F(t0)=U –
|
|
34. приращение функции в точке t0 => U=dU+(1/2!)d2U+…+(1/n!)dnU+(1/(n+1)!)dn+1U() (3) t0<<t0+t; M(x0+x,y0+y)O(,M0). Соединим М0 и М прямой. q={x,y}. Уравнение прямой: (x-x0)/x=(y-y0)/y или x=x0+tx, y=y0+ty (4); (x0,y0)->t=0, (x0+x,y0+y)->t=1 => 0 t 1. Таким образом можно считать, что на [0,1] задана сложная функция U=f(x,y), где x=x0+tx, y=y0+ty. Эта функция (t+1) раз дифференцируема на этом отрезке, т.к. f,x и y (n+1) раз дифференцируемы в своих областях определения. Обозначим эту сложную функцию через F(t). И запишем ее разложение в точке t0 в виде (3) U=F(1)-F(0)=F(M)-F(M0). В формуле (3) все дифференциалы – дифференциалы сложной функции U=f(x,y), где x и y – линейные функции переменной t. в этом случае инвариантность дифференциала любого порядка не нарушается. Поэтому: dk(t0)=(/xdx+/ydy)kU(M0)= dkU(M0); dn+1U[t+(t-t0)]=(/xdx+/ydy)n+1U(N)=dn+1U(N), где N=(x0+1x, y0+2y), 0<1,2<1. Согласно (4) dx=dtx, dy=dty (6) Подставив (5) и (6) в (3), получим формулу Тейлора (1) |
35. Локальная формула Тейлора функции многих переменных с остаточным членом в форме Пеано (формулировка). Теорема: Пусть u=f(M)=f(x1,..,xm) задана и (n-1) раз дифференцируема в окрестности точки М0(x10,...,xm0) и n раз дифференцируема в самой точке М0. Тогда MO(,M0) : f(M)=f(M0)+k=1n(dku(M0/k!)+o(n), где =(М,М0)0 при ММ0 |
|
36. Экстремум функции многих переменных. Необходимые условия экстремума. Пусть u=f(M)=f(x1,..,xn) определена на множестве Х, а М0(x01,..,x0n) Определение: точка М0 называется точкой локального максимума (минимума), если существует такая окрестность точки М0, что для всех точек, принадлежащих этой окрестности: f(M)f(M0) (f(M)f(M0)). В случае строгого выполнения неравенств М0 – точка строгого максимума (минимума) Определение: точки максимума (минимума) функции называются точками экстремума (строгого или нестрогого). Замечание: если u=f(M)-f(M0), то в указанной окрестности u<=0 (max) и u>=0 (min). Теорема (необходимое условие): u=f(x1,...,xn), M0(x10,...,xn0), M0 – точка экстремума в f(M). Тогда, если в этой точке существует частная производная, то она равна 0. Доказательство: Пусть существует частная производная f/x1, если M0(x10,..,xn0), M0 – точка экстремума для u=f(x1,...,xn), то эта точка – точка экстремума и для f(x1,x20,...,xn0). Эта функция – функция одной переменной (х1). Т.к. в этой точке существует f/x1, то, по теореме Ферма, она равна 0. f(x1,x20,...,xn0)/x1|x1=x01=0. Аналогично теорема доказывается для частных производных и по другим переменным. Следствие: Если f(x) дифференцируема в точки экстремума, то ее дифференциал в этой точке равен 0. |
37. Достаточные условия экстремума функции многих переменных. Теор. Пусть функция U = f(M) = f(x1,...,xn) один раз дифференцируема в окресности точки M0= (x10,...,xn0) и 2 раза дифференцируема в самой точке M0. Пусть эта точка M0 является стационарной точкой функции U = f(M). Т.е. dU(M0) = 0. Тогда если второй диференциал d²U(M0) представляет собой квадратичную форму от диференциала dx1,...dxn является знакоопределенной квадратичной формой, то функция f(M) имеет в точке M0 экстремум, причем если d²U(M0) > 0 – то min, если d²U(M0) < 0 - то max. Если d²U(M0) - знакопеременная квадратичная форма, то экстремума нет. Дока-во. 1. Пусть d²U(M0) - положительно определенная квадратичная форма от dx1,...,dxn. Докажем, что в этом случае M0 – точка локального min. Разложим U = f(M) в окресности точки M0 по локальной формуле Тейлора в виде: ∆U = dU(M0) + (1/2!)* d2U(M0) + o(ρ2) (1), где ∆U = f(M) – f(M0), ρ = ((x1 – x10)2 + ... + (xn - xn0). 2)1/2 = (dx12 + ... + dxn2)1/2 (2) Здесь все условия о разложении функции в M0 по формуле Тейлора с остаточным членом в форме Пеано – выполнены. Т.к. M0 – стационарная точка, то dU(M0) = 0; ∆U = dU(M0) + (1/2!)* d2U(M0) + o(ρ2)= (1/2)*i=1∑n*k=1∑n (aik(xi – xi0)(xk – xk0) + o(ρ2)) (3), где aik = aki = ∂²U/∂xi∂xk (4) Достаточ доказат, что. при достаточно малых ρ правая часть (3) положитлна. Введем обозн-я: hi = (xi – xi0)/ρ ; | hi | ≤ 1; h12 + ... + hn2 = 1 (5) С помощью этих обозначений выражение (3) переходит в |
|
37.2 ∆U = (ρ2/2)[i=1∑n*k=1∑n(aikhihk)] + o(ρ²) = (ρ2/2)[ i=1∑n*k=1∑n(aikhihk + (ρ)] (6), = 2o(ρ2)/ρ2 -> 0 при ρ -> 0. Здесь квадратичная форма: φ = i=1∑n*k=1∑n(aikhihk) (7), которая по условию положительно определена представляет собой функцию переменных h1 ... hn, которая непрерывна на поверхности единичной сферы (5), причем эта сфера представляет собой замкнутое и ограниченное множество. По второй теореме Виерштрасса эта функция на данной сфере достигает своей точной нижней грани , которая по причени положительной определенности квадратичной формы d²U(M0) и из того, что согласно (5) все hi одновременно в ноль не обращаются - сторого положительна, т.е. > 0. Поскольку (ρ) – б.м.ф. при ρ -> 0 то для этого > 0 δ >0 ρ<δ: |(ρ)| < => для этих значений ρ правая часть (6) больше нуля. Т.е. эта величина больше нуля для всех точек М достаточно близких к M0: ∆U = f(M) – f(M0) > 0, в точке M0 – локальный min. Аналогично для локального max (d²U(M0) < 0)
φ’ = φ(h1’,...,hn’) > 0 ; φ’’ = φ(h1’’,...,hn’’) > 0. Для достаточно малых ρ: φ’ + ’(ρ) > 0 ; φ’’ + ’’(ρ) < 0 (8) существует окресность согласно (6), (7), (8) где: ∆U(M0) > 0 и ∆U(M0) < 0; M’ и M’’: ∆U = f(M’) – f(M0) > 0 и ∆U = f(M’’) – f(M0) < 0 и экстремума нет. Замечание: Если d²U(M0) – квази знакоопределенная квадратичная форма, то f(M) - в стационарной точке M0 может иметь, а может и не иметь экстремума |
|
|
39. Теорема о существовании, единственности и непрерывности неявной функции, определяемой одним уравнением с двумя переменными. Теорема. Пусть функция F(x,y) непрерывна в некоторой окресности U(M0) точки M0 (x0,y0). Пусть она имеет в этой окресности часную производную Fy’(x,y), которая непрерывна в точке M0, причем F(x0,y0) = 0 и Fy’(x0,y0) ≠ 0 .Тогда найдется окресность точки U(x0) и U(y0), что для xU(x0) cуществует единственное решение y = f(x)U(x0) уравнения F(x,y) = 0, причем это решение непрерывно в U(x0) и выполняется равенство y0 = f(x0). Доказательство. 1. Существование и единственность. Пусть: Fy’(x0,y0)>0. Выберем прямоугольную окресность U(M0) так, чтобы F(x,y) была непрерывна на замкнутой окресности этой точки U(M0, δ0, η) = {(x,y) | |x-x0| ≤ δ0, |y-y0| ≤ η} и так, чтобы для MU(M0, δ0, η) выполнялось условие Fy’(x,y) > 0. Это всегда можно сделать согласно теореме о сохранениии знака непрерывной функции. Пусть x0 - фиксированная точка, т.к. в окресности U: Fy’ > 0, то функция φ(y) = F(x0,y) сторого монотонно возрастает на [y0 - η, y0 + η]. По условию теоремы F(x0,y0) = 0 , т.е. φ(y0) = F(x0,y) = 0 F(x0,y0 - η) = φ(y0 - η) < 0 (1) ; F(x0,y0 + η) = φ(y0 + η) > 0 (2) Зафиксируем у. Т.к. функция F(x,y) непрерывна в точках (x0,y0 - η) и (x0,y0 + η), то функции F(x0,y0 - η) и F(x0,y0 + η) будут непрерывны в x0, как функции от х. Т.к. функции непрерывны по совокупности аргументов – непрерывны и по каждому аргументу в отдельности. Поэтому существует такая окресность точки x0 - U(x0, δ) = (x0 - δ, x0+ δ) , где по свойству |
39. 2 сохранения знака непрерывной функции F(x0, y0 - η) < 0 и F(x0, y0 + η) > 0 для xU(x0, δ). См. (1) и (2). При этом δ < δ0. Рассмотрим окресность точки y0 = U(y0, η) = (y0 - η, y0 + η). Зафиксируем xU(x0, δ) и будем рассматривать F(x,y) как функцию одного переменного на [y0 - η, y0 + η] для этого фиксированного x. По условию теоремы на этом отрезке существует часная производная Fy’(x,y) > 0, по этому функция F(x,y) непрерывна и сторого монотонно возрастает, причем F(x, y0 - η) < 0 и F(x, y0 + η) > 0. Согласно теореме о промежуточном значении функции, непрерывной на отрезке, для любой фиксированной точки xU(x0,δ) существует точка yU(y0, η), что F(x,y) = 0. В силу строгой моноонности значение y единственно. xU(x0,δ) мы имеем единственную yU(y0, η), т.е. между {x} и {y} имеем однозначное соответствие т.е. y = f(x) или y = f(x) при этом xU(x0,δ), yU(y0, η). Кроме того F(x,y) = 0. В следствии однозначного соответствия эта функция единственна из F(x0,y0) = 0 => y0 = f(x0). Существование и единственность доказаны.
а) F(x,y) непрерывна в заданной U(M0,δ,η) (следует из условия теоремы). б) F(x,f(x)) = 0 в) Fy’(x,y) > 0 для (x,y)U(M0,δ,η) г) Точка (x,f(x))U(M0,δ,η) для xU(x0,δ) Таким образом для любой точки (x,f(x)) удовлетворяющей условию (2) можно провести те же построения что и для точки (x0,y0) => f(x) непрерывна в окресности U(x0,δ). |
|
39.3 сохранения знака непрерывной функции F(x0, y0 - η) < 0 и F(x0, y0 + η) > 0 для xU(x0, δ). См. (1) и (2). При этом δ < δ0. Рассмотрим окресность точки y0 = U(y0, η) = (y0 - η, y0 + η). Зафиксируем xU(x0, δ) и будем рассматривать F(x,y) как функцию одного переменного на [y0 - η, y0 + η] для этого фиксированного x. По условию теоремы на этом отрезке существует часная производная Fy’(x,y) > 0, по этому функция F(x,y) непрерывна и сторого монотонно возрастает, причем F(x, y0 - η) < 0 и F(x, y0 + η) > 0. Согласно теореме о промежуточном значении функции, непрерывной на отрезке, для любой фиксированной точки xU(x0,δ) существует точка yU(y0, η), что F(x,y) = 0. В силу строгой моноонности значение y единственно. xU(x0,δ) мы имеем единственную yU(y0, η), т.е. между {x} и {y} имеем однозначное соответствие т.е. y = f(x) или y = f(x) при этом xU(x0,δ), yU(y0, η). Кроме того F(x,y) = 0. В следствии однозначного соответствия эта функция единственна из F(x0,y0) = 0 => y0 = f(x0). Существование и единственность доказаны.
а) F(x,y) непрерывна в заданной U(M0,δ,η) (следует из условия теоремы). б) F(x,f(x)) = 0 в) Fy’(x,y) > 0 для (x,y)U(M0,δ,η) г) Точка (x,f(x))U(M0,δ,η) для xU(x0,δ) Таким образом для любой точки (x,f(x)) удовлетворяющей условию (2) можно провести те же построения что и для точки (x0,y0) => f(x) непрерывна в окресности U(x0,δ). |
40. Теорема о дифференцируемости неявной функции, определяемой одним уравнением с двумя переменными. Теорема. Если неявная функция существует, единственна и непрерывна, то она имеет в некоторой точке (x0,y0) производную Fx’(x,y), коорая непрерывна в (x0,y0) и функция f(x) имеет в x0 производную, причем fx’(x0)= -Fx’(x0,y0)/ Fy’(x0,y0). Доказательство. Пусть в окрестности U(M0) существуют непрерывные в этой точке частные производные Fx’ и Fy’, тогде F(x,y) дифференцируема в точке (x0,y0) по достаточному признаку дифференцирования: F(x0+x, y0+y)-F(x0,y0)=Fx’(x0,y0)x + Fy’(x0,y0)y + 1x + 2y (1), где lim(1)= lim(1)=0 при =(x2+y2)1/2->0. Пусть в (1) x0+x U(x0), y=f(x0+x)-f(x0), значит f(x0+y)= f(x0+x) => y0+y=f(x0+x). Т.к. F(x,f(x))=0, то F(x0+x, y0+y)= F(x0+x, f(x0+x))=0. Т.к. F(x0,y0)=0, то мы имеем: Fx’(x0,y0)x + Fy’(x0,y0)y + 1x + 2y = 0 => y/x= -(Fx’(x0,y0) +1())/(Fy’(x0,y0) +2()) (2). Пусть x->0. Т.к f(x) непрерывна в x0, то y->0, значит при x->0 ->0. Отсюда в (2) lim(1())= lim(2())=0 при x->0. Поэтому при x->0 предел в правой части (2) существует и равен -Fx’(x0,y0)/ Fy’(x0,y0)=> при x=0 fx’(x0)= -Fx’(x0,y0)/ Fy’(x0,y0) по условию теоремы Fy’(x0,y0)0 .
|
|
41. Вычисление производных неявных функций, заданных системой уравнений. Пусть даны Exn и Eym – евклидовы пространства точек x=(x1,…,xn) и y=(y1,…,ym). Рассмотрим (m+n)-мерное пространство точек (x,y) Ex,y(m+n). Пусть AExn и BEym. Определение. Декартовым произведением AxB называется множество всех упорядоченных совокупностей n+m чисел вида (x1,…,xn ; y1,…,ym)=(x,y), где xA и yB. Пусть дана система уравнений Fi(x,y)=0, где i=1,…,m; {F1(x1,…,xn ; y1,…,ym)=0,… Fm(x1,…,xn ; y1,…,ym)=0 (1). Предположим, что y1=1(x1,…,xn) и ym=m(x1,…,xn) являются решениями системы (1). Пусть функции, стоящие в правой части системы (1) имеют частные производные. Составим матрицу из этих производных: (F1/y1, F2/y1,…, Fm/y1; F1/y2, F2/y2,…, Fm/y2;…; F1/ym, F2/ym,…, Fm/ym) – матрица Якоби. Определитель этой матрицы называется якобианом системы функций F1,…,Fm по переменным y1,…,ym. Если предположить, что
|
41.существует решение системы (1), то мы будем считать, что y1,…,yn заданы как неявные функции переменных x1,…,xn. Теорема. Пусть 1) функция Fi(x,y)= Fi(x1,…,xn ; y1,…,ym) непрерывно дифференцируема в некоторой окрестности точки M0(x10,…,xn0; y10,…,yn0); 2) точка M0 удовлетворяет системе, т.е i (i=1,…,m): Fi(x10,…,xn0; y10,…,yn0)=0; 3) якобиан системы отличен от нуля. Тогда 1) Fi(x,y) определяет систему y1,…,ym как однозначную функцию от x1,…,xn; 2) при x=x0 эти функции принимают значение yi0=fi(x10,…,xn0); 3) f1,….,fm непрерывны и имеют непрерывные частные производные по всем аргументам. Доказательство. Без доказательства. |
|
42. Понятие отображения. Дифференцируемое отображение и его дифференциал. Матрица Якоби и Якобиан системы функций, их свойства. Отображения. Пусть xn = {(x1 ... xn)} – множество точек пространства Xn; ym = {(y1 ... ym)} - Ym. Поставим в соответствие каждой точке х (xXn) точку у (yYm), с помощью некоторого закона f. Тогда говорят, что на множестве xn задано отображение f. {y1 = f1(x1,...,xn);...;ym = fm(x1,...,xn) (1) или y = f(x); Ym - образ множества Xn. Опр-е 1. Отображение (1) называется: 1) взаимооднозначным, если различным точкам Xn ставятся в соответствие различные точки Ym; 2) непрерывным x0Xn если каждая из функций системы (1) непрерывна в точке x0 Опр-е 2. . Отображение f называется дифференцируемым в точке x0, если в некоторой окресности точки x0 ∈ Х выполняется условие: f(x0 + ∆x) – f(x0) = D∆x + o(∆x) (2). Где: 1) x0 + ∆x = (x10 + ∆x1,..., xn0 + ∆xn)∈X; 2) D – непрерывное линейное отображение, т.е. линейный оператор D: X -> Y; D∆x ∈ Y; 3) Вектор o(∆x)∈Y; lim((||o(∆x)||/||∆x||) = 0 при x->0, где о(∆x) = (о1(∆x); ...;оn(∆x)) (столбец). В левой части выражения (2) стоит приращение отображение f в x0. D∆x - главная лаинейная часть этого приращения при изменении x от x0 до x0 + ∆x; : f(x0 + ∆x) – f(x0) ≃ D∆x. Опр-е3. Опертор D в формле(2) назывся произвдной отобржния f в x0: D=f’(x0). Опр-е 4. Выражение D∆x есть вектор или точка в пространстве Y и этот вектор получается применением оператора D к вектору приращения x. Это называется дифференциалом отображения f в точке x0: D∆x = df(x) = f’(x)∆x = f(x)dx; dx = ∆x = (∆x1,…,∆xn) = (dx1,...,dxn). Диференциал отображения : Матрицы: (∂f1/∂x1 ... ∂f1/∂xn; ...; ∂fm/∂x1 ... ∂fm/∂xn) * (∆x1; ...; ∆xn) = ((∂f1/∂x1)∆x1 ... (∂f1/∂xn)∆x1; ... ; (∂fm/∂x1)∆x1 ... (∂fm/∂xn)∆xn). |
42. 2 Опр-е 5. Отображение диффер-ое в каждой точке области наз-ся дифференцируемым отображением в этой области. Матрица Якоби и Якобиан системы функций. Пусть даны Exn и Eym – евклидовы пространства точек x=(x1,…,xn) и y=(y1,…,ym). Рассмотрим (m+n)-мерное пространство точек (x,y) Ex,y(m+n). Пусть AExn и BEym. Опр-е 6. Декартовым произведением AxB называется множество всех упорядоченных совокупностей n+m чисел вида (x1,…,xn ; y1,…,ym)=(x,y), где xA и yB. Пусть дана система уравнений Fi(x,y)=0, где i=1,…,m; {F1(x1,…,xn ; y1,…,ym)=0,… Fm(x1,…,xn ; y1,…,ym)=0 (1). Предположим, что y1=1(x1,…,xn) и ym=m(x1,…,xn) являются решениями системы (1). Пусть функции, стоящие в правой части системы (1) имеют частные производные. Составим матрицу из этих производных: (F1/y1, F2/y1,…, Fm/y1; F1/y2, F2/y2,…, Fm/y2;…; F1/ym, F2/ym,…, Fm/ym) – матрица Якоби. Определитель этой матрицы называется якобианом системы функций F1,…,Fm по переменным y1,…,ym. Если предположить, что существует решение системы (1), то мы будем считать, что y1,…,yn заданы как неявные функции переменных x1,…,xn. Свойства матрицы Якоби и якобианов отображения. Теор. Пусть дано отображение f: Xn -> Ym ; y = f(x) и отображение g: Ym → Zp; z = g(y). Xn, Ym, Zp - открытые множества евклидова пространства, соответственно размерности n,m,p. Причем f, g – непрерывно диференцируемые отображения. Тогда суперпозиция этих отображений является напрерывно диференцируемым отображением Xn → Zp; z = g(f(x)). И матрица Якоби суперпозиции отображений в каждой точке множества Xn равна произведению матриц Якоби отображений f, g; т.е. (∂zi/∂xk) = (∂zi/∂ys)*(∂ys/∂xk). Доктельство. Все эти отображения задаются с помощью числовых функций, |
|
42.3 по этому непрерывное диференцированние отображения g(f(x)) сразу следует из теоремы о дифференцировании сложной функции и теоремы о непрерывности сложной функции. Матрица (∂zi/∂ys) содержит p – строк и m – столбцов, а матрица (∂ys/∂xk) : m – строк и n – столбцов Т.е. произведение (∂zi/∂ys)*(∂ys/∂xk) : p – строк и – n столбцов. Но по правилу диференцирования сложной функции (∂zi/∂xk) = ∑ (∂zi/∂ys)*(∂ys/∂xk) i=1,...,p; k=1,...n и матрица (s=1∑m(∂zi/∂ys)*(∂ys/∂xk)) – произведение указанных матриц. (∂zi/∂xk) = (∂zi/∂ys)*(∂ys/∂xk). Следствие 1. Если выполняется условие теоремы при m = n = p, то якобиан суперпозиции отображений равен произведению якобианов этих отображений. (∂(z1...zn)/∂(x1...xn)) = (∂(z1...zn)/∂(y1...yn))*(∂(y1...yn)/∂(x1...xn)) Следствие 2. Если y = f(x) отображение класса C¹ Xn -(f)-> Ym (Xn, Ym - открытые множества) и x = f-1(y) является обратным отображением, которое однознозначно и непрерывно дифференцируемо в своей области определения Ym, то: (∂(y1...ym)/∂(x1...xn))*((x1...xm)/∂(y1...yn)) = 1 или: ((x1...xn)/∂(y1...yn)) = (1/ (∂(y1...yn)/∂(x1...xn)) |
43. Регулярное отображение и его свойства. Пусть дана система функций y = f(x): {y1 = f1(x1,...,xn);...;yn = fn(x1,...,xn) (1) Эта система задает отображение f. Пусть xX, yY. Y - образ X при отображении f. Определение. Отображение f осуществляемое системой (1) называется регулярным в некоторой замкнутой области ХЕⁿ, если: 1) это отображение принадлежит классу С1; 2) якобиан D(f1,...,fn)/D( x1,...,xn)) ≠ 0 Свойства регулярных отображений: Теорема 1 (о локальной обратимости регулярного отображения). Пусть 1) y = f(x) (1) - отображение класса С¹ открытого множества GЕⁿ в Еⁿ; 2) якобиан этого отображения в точке х0G отличен от нуля. Тогда в окресности точки y0 = f(x0) существует обратное отображение, которое регулярно. Доказательство. Без доказательства. Теорема 2. Если отображение f регулярно в открытом множестве GЕⁿ, то образ множества G (f(G)) также открытое множество.
|
|
43. Доказательство. Пусть y = f(x) – регулярное отображение множества G-> Еⁿ. Пусть y0 произвольная точка y0 = f(x0). Пусть x0 – прообраз этой точки y0, т.е. x0 = f-1( f(x0)) или xº = f-1(y0), при y0 = f(x0). По теореме 1 существует такая окрестность точки x0: U(x0)G и существует такая окресность точки y0: U(y0) f(G) . U(x0) отображение в окресности U(y0) f(G). Таким образом каждая такая точка – внутренняя => образ отображения f : f(G) - открытое множество. Следствие: Регулярное отображение каждую граничную точку переводит в граничную. Лемма 1. Регулярное отображение непрерывную кривую переводит в непрерывную кривую принадлежащую множеству образов. Лемма 2 (принцип сохранения области). Регулярное отображение область переводит в область. |
44. Понятие зависимости системы функций. Теорема о необходимых условиях зависимости. Формулировка достаточных условий зависимости. Определение
1. Пусть на
некотором открытом множестве G
Определение 2. Если среди функций системы (1) есть функция, зависимая от остальных на множестве G, то эта система называется системой на множестве G. В противном случае – независимой на G. Используем
матрицу Якоби:
Теорема
1. (Необходимое
условие зависимости): Пусть m Доказательство:
Т.к. система (1) – линейно зависима от
G,
тогда пусть функция
m =Ф(1(x),…, m-1(x)), xG; ym = (y1,...,ym-1). – непрерывно дифференцируемая функция от (m-1) аргументов : y1,...,ym-1 Найдем производную от сложной функции ’: ∂ym/∂xk = (∂/∂y1)*(∂y1/∂x1) +...+ (∂/∂ym-1)*( ∂ym-1/∂xk) Это выражение показывает, что m – строка матрицы Якоби (2) есть линейная комбинация остальных строк этой матрицы, значит ее можно вычеркнуть не изменяя ранга матрицы => Rg(2) < m в любой точке xG. Следствие
1. Если m
= n,
и система функций зависима на множестве
G,
то ее якобиан
Следствие
2. (Достаточное
условие независимости системы
функций). Пусть m
Доказательство. Предположим, что система зависима. Тогда по теореме (1) ранг матрицы Якоби меньше m, что противоречит условию. Теорема 2 (достаточное условие зависимости системы функций). Пусть у матрицы (2) системы функций (1) некоторый минор порядка r отличен от нуля в точке x0 G и пусть все миноры r+1 порядка равны нулю в некоторой окресности точки x0Rg (2) не превосходит r. Тогда r функций, входящих в этот минор r порядка, независимы в окрестности точки xº и каждая из остальных функций зависит от указанных r функций. Док-во. Без доказательства.
|

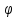 (x)
= F1(x)
– F2(x);
F1(x)
и F2(x)
дифференцируемы на ]a,b[
=>φ(x)
тоже, при этом φ’(x)
= (F1(x)
– F2(x))’
= F1’(x)
– F2’(x)
= f(x)
– f(x)
= 0. Но если производная равна нулю на
]a,b[,
то φ(x)
= С: F1(x)
– F2(x)
= C.
(x)
= F1(x)
– F2(x);
F1(x)
и F2(x)
дифференцируемы на ]a,b[
=>φ(x)
тоже, при этом φ’(x)
= (F1(x)
– F2(x))’
= F1’(x)
– F2’(x)
= f(x)
– f(x)
= 0. Но если производная равна нулю на
]a,b[,
то φ(x)
= С: F1(x)
– F2(x)
= C.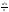 =ln|x|+C
(x≠0)
5)∫axdx=
=ln|x|+C
(x≠0)
5)∫axdx= +C
(a≠1;a>0)
∫exdx=ex+C;
6)∫sinxdx=-cosx+C;
7)∫cosxdx=sinx+C;
8)∫
+C
(a≠1;a>0)
∫exdx=ex+C;
6)∫sinxdx=-cosx+C;
7)∫cosxdx=sinx+C;
8)∫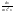 =tgx+C
(x≠
=tgx+C
(x≠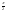 +πk)
9)∫
+πk)
9)∫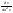 =-ctgx+C
(x≠πk)
10)∫
=-ctgx+C
(x≠πk)
10)∫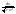 ={
={
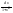 ={
={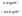 12)∫
12)∫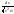 =ln|x+
=ln|x+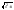 |+C
13)∫
|+C
13)∫ =
=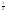 ln|
ln|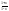 |+C
(|x|≠1);
14)∫chxdx=shx+C
15)∫shxdx=chx+C
16)∫
|+C
(|x|≠1);
14)∫chxdx=shx+C
15)∫shxdx=chx+C
16)∫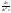 =thx+C;
17)∫
=thx+C;
17)∫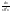 =-cthx+C
(x≠0)
=-cthx+C
(x≠0)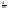 F(φ(x))=
F(φ(x))=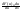 =f(u)*
=f(u)*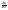 |u=φ(x)=f(φ(x))φ’(x),
т.е. F(φ(x))
является первообразной для f(φ(x))φ’(x).
∫f(u)du|u=φ(x)=F(u)+C=F(φ(x))+C;
∫f(φ(x))φ’(x)dx=∫f(u)du|u=φ(x)
(3).
|u=φ(x)=f(φ(x))φ’(x),
т.е. F(φ(x))
является первообразной для f(φ(x))φ’(x).
∫f(u)du|u=φ(x)=F(u)+C=F(φ(x))+C;
∫f(φ(x))φ’(x)dx=∫f(u)du|u=φ(x)
(3).
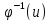 ,
необходимо, чтобы u=
,
необходимо, чтобы u=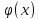 была строго монотонной. В этом случае:
∫f(u)du=
∫f(φ(x))φ’(x)dx
была строго монотонной. В этом случае:
∫f(u)du=
∫f(φ(x))φ’(x)dx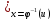 (4)
(4) интеграл
∫vdu,
то также
интеграл
∫vdu,
то также ∫udv,
причём ∫udv=uv-∫vdu.
∫udv,
причём ∫udv=uv-∫vdu. - рациональная функция (1); Pn(x)
и Qn(x)
– многочлены; n≥m;
- рациональная функция (1); Pn(x)
и Qn(x)
– многочлены; n≥m;
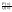 -
правильно-рациональная дробь(несократимая).
Основная теорема алгебры всякий
многочлен ненулевой степени имеет
хотя бы 1 корень. Всякий многочлен n-ой
степени имеет n
число корней, включая кратных,
действительных и комплексных.
-
правильно-рациональная дробь(несократимая).
Основная теорема алгебры всякий
многочлен ненулевой степени имеет
хотя бы 1 корень. Всякий многочлен n-ой
степени имеет n
число корней, включая кратных,
действительных и комплексных. ;
2)
;
2) ;
(k≥2;k
;
(k≥2;k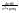
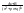 ≥
≥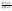 -правильно-рациональная
дробь несократимая с вещественными
числами, знаменатель дроби: Q(x)=(x-a1)
-правильно-рациональная
дробь несократимая с вещественными
числами, знаменатель дроби: Q(x)=(x-a1) …
(x-ak)
…
(x-ak) (x2+p1x+q)
(x2+p1x+q) (x2+psx+qs)
(x2+psx+qs) α,
s,
λ
– натуральные числа:
α,
s,
λ
– натуральные числа:
 (αkxk)dx=
(αkxk)dx= αk
αk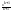 +C,
рассмотрим дроби 1-го; 4-го типов
+C,
рассмотрим дроби 1-го; 4-го типов dx=Aln|x-b|+C
2.∫
dx=Aln|x-b|+C
2.∫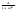 dx=A
dx=A 3.∫
3.∫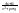 ∫
∫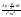 dt=
A∫
dt=
A∫ +(N-
+(N- )∫
)∫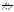 =
=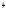 ln(t2+a2)+
ln(t2+a2)+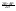 arctg
arctg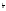 +C;
t=x+
+C;
t=x+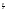 ;
x2+px+q=(x+
;
x2+px+q=(x+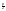 )2+(q-(
)2+(q-(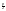 )2;
4.
)2;
4.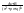
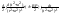 =
=
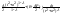 ;
;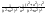 ;
;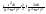
 -
-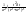 =
= (6);
(6);
 (7)
(7)
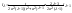 (8)
(8)
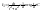
 ,
где P
и Q
– многочлены от x,y,…z
называются рациональной функцией от
x,y,..z;
Если x=φ1(t),
y=φ2(t),…,z=φn(t);
то R(φ1(t),…,φn(t))
называется рациональным многочленом
от φ1(t),…,φn(t).
,
где P
и Q
– многочлены от x,y,…z
называются рациональной функцией от
x,y,..z;
Если x=φ1(t),
y=φ2(t),…,z=φn(t);
то R(φ1(t),…,φn(t))
называется рациональным многочленом
от φ1(t),…,φn(t).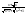 -
рациональная функция от x,
-
рациональная функция от x, ,
, -1,
-1,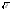 -1 2)f(x)
=
-1 2)f(x)
=
 =
R(sinx,cosx,tgx).
=
R(sinx,cosx,tgx).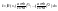 ,
где r1,…,r2-рациональные
числа.
,
где r1,…,r2-рациональные
числа. конечное
множество точек x1,x2,..,xn,
такие, что a=x0<x1<x2<…<xn-1<xn=b;
T{xi};
T={x0;x1;…;xn}
[xi-1;xi]-отрезок
разбиения; Δxi=xi-xi-1-длина
отрезка разбиения; δT-характеристика
разбиения(максимальная длина отрезка
множества отрезков разбиения) Свойства
разбиений отрезка: 1)Если Т1<T2
и
Т2<T3=>T1<T3;
2)Если
конечное
множество точек x1,x2,..,xn,
такие, что a=x0<x1<x2<…<xn-1<xn=b;
T{xi};
T={x0;x1;…;xn}
[xi-1;xi]-отрезок
разбиения; Δxi=xi-xi-1-длина
отрезка разбиения; δT-характеристика
разбиения(максимальная длина отрезка
множества отрезков разбиения) Свойства
разбиений отрезка: 1)Если Т1<T2
и
Т2<T3=>T1<T3;
2)Если
 Т1
и
Т1
и
 Т2
Т;
Т>T1и
Т>T2
Т2
Т;
Т>T1и
Т>T2 называется интегральной суммой Римана
функции f(x)
, соответствует данному разбиению
Т[a;b]
и данному выбору точек ξi
на отрезках разбиения [xi-1;xi].
Число I
называется пределом интегрируемой
суммы σ(Т,si)
при δT->0;
называется интегральной суммой Римана
функции f(x)
, соответствует данному разбиению
Т[a;b]
и данному выбору точек ξi
на отрезках разбиения [xi-1;xi].
Число I
называется пределом интегрируемой
суммы σ(Т,si)
при δT->0;
 ε>0
δ(ε)>0,
ε>0
δ(ε)>0,
 Tє[a;b]
при условии δT
<δ и ξi=>
|σ (Т,si)-I|<ε
или I=
Tє[a;b]
при условии δT
<δ и ξi=>
|σ (Т,si)-I|<ε
или I=
 σ(Т,ξi).
σ(Т,ξi).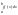 (a-нижний
предел; b-верхний
предел)
(a-нижний
предел; b-верхний
предел)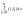 =
f(ξi)Δx1+A.
σ(Т,ξi)≥
|f(ξi)|Δx1-|A|;
т.к. f(x)
неограниченна на [x0;x1],
то по определению ограниченности
=
f(ξi)Δx1+A.
σ(Т,ξi)≥
|f(ξi)|Δx1-|A|;
т.к. f(x)
неограниченна на [x0;x1],
то по определению ограниченности
 M>0
ξ0є
[x0;x1]:
|f(ξi)|>
M>0
ξ0є
[x0;x1]:
|f(ξi)|>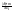 =>
|σ(Т,ξi)|>M,
т.е. для
=>
|σ(Т,ξi)|>M,
т.е. для
 разбиения
такое множество точек ξi,
что интегральную сумму можно сделать
больше заданного числа. Это означает
неограниченность интегральных сумм,
а значит предел интегральных сумм при
δT->0
разбиения
такое множество точек ξi,
что интегральную сумму можно сделать
больше заданного числа. Это означает
неограниченность интегральных сумм,
а значит предел интегральных сумм при
δT->0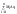 -верхняя
сумма. s=m1Δx1+…+mnΔxn=
-верхняя
сумма. s=m1Δx1+…+mnΔxn= -
нижняя сумма.
-
нижняя сумма. T:
s≤S
2)
T:
s≤S
2)
 σ
соответствующей T
s≤I
≤S;
mi≤f(ξi)≤Mi
σ
соответствующей T
s≤I
≤S;
mi≤f(ξi)≤Mi
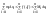 ;
; фиксированного
разбиения Т и
фиксированного
разбиения Т и
 ε>0
промежуточные точки ξiє[xi-1;xi]:0≤S-
σ(Т,ξi)<ε;
0≤ σ(Т,ξi)-s<ε;
ε>0
промежуточные точки ξiє[xi-1;xi]:0≤S-
σ(Т,ξi)<ε;
0≤ σ(Т,ξi)-s<ε; ε>0
ξiє[xi-1;xi]:f(ξ)≤Mi;
б)
ε>0
ξiє[xi-1;xi]:f(ξ)≤Mi;
б)
 ε>0 ξiє[xi-1;xi]:f(ξi)>M-
ε>0 ξiє[xi-1;xi]:f(ξi)>M-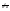 ;
0≤ Mi-f(ξi)<
;
0≤ Mi-f(ξi)< (i=1,2…,n).
Умножим неравенство на Δxi
и просуммируем.
(i=1,2…,n).
Умножим неравенство на Δxi
и просуммируем.
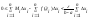 ;
0≤ S-σ(Т,ξi)<ε.
Второе неравенство доказывается
аналогично.
;
0≤ S-σ(Т,ξi)<ε.
Второе неравенство доказывается
аналогично. σє{σ(Т,ξi)};
σ≤S(T)
б) согласно свойству 1)
σє{σ(Т,ξi)};
σ≤S(T)
б) согласно свойству 1)
 ε>0
σє{σ(Т,ξi)};
S-σ<ε
или σ>S-є
=> S=sup{σ(Т,ξi)};
Второе утверждение доказывается
аналогично.
ε>0
σє{σ(Т,ξi)};
S-σ<ε
или σ>S-є
=> S=sup{σ(Т,ξi)};
Второе утверждение доказывается
аналогично.
 2
разбиения [a;b],
тогда справедливо неравенство:
s(T’)≤S(T’’)
и s’≤S’’;
Любая нижняя сумма не превосходит
верхнюю сумму.
2
разбиения [a;b],
тогда справедливо неравенство:
s(T’)≤S(T’’)
и s’≤S’’;
Любая нижняя сумма не превосходит
верхнюю сумму. разбиений
T’
и T’’
отрезка [a;b]
T:T>T’
и T>T’’.
Согласно свойству 2) имеем
s(T’)≤s(T)≤S(T)≤S(T’’)
и s’≤s≤S≤S’’
разбиений
T’
и T’’
отрезка [a;b]
T:T>T’
и T>T’’.
Согласно свойству 2) имеем
s(T’)≤s(T)≤S(T)≤S(T’’)
и s’≤s≤S≤S’’ =inf{S};
=inf{S};
 =sup{s};
=sup{s}; и
и называются верхним и нижним интегралом
Дарбу. Из свойства 3)
называются верхним и нижним интегралом
Дарбу. Из свойства 3)
 T:
T:
 ≤
≤ ;
s≤
;
s≤ ≤
≤ ≤S
≤S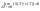 (1)
(1) ε>0
ε>0
 δ(ε)>0
δ(ε)>0 T
δT<δ=>|S-s|<ε
T
δT<δ=>|S-s|<ε I;I=
I;I=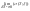 ;
; ε>0
δ(ε)>0:
ε>0
δ(ε)>0:
 T
δT<δ
T
δT<δ
 выбора
точки ξ; => |σ-I|<ε
=> I-ε<σ<I+ε;
s=infσ;
S=supσ
=> Для T
и δT<δ
будет выполняться I-ε<s<S<I+ε;
s≤{σ}
и S≤{σ}
=> |S-I|<ε
и |s-I|<ε
=> |S-I|
+ |s-I|
< 2ε => x-S+s-I<2ε=>S-s<2ε,
т.е. выполняется (1)
выбора
точки ξ; => |σ-I|<ε
=> I-ε<σ<I+ε;
s=infσ;
S=supσ
=> Для T
и δT<δ
будет выполняться I-ε<s<S<I+ε;
s≤{σ}
и S≤{σ}
=> |S-I|<ε
и |s-I|<ε
=> |S-I|
+ |s-I|
< 2ε => x-S+s-I<2ε=>S-s<2ε,
т.е. выполняется (1)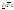 S
(2) выполняется, то отсюда s≤
S
(2) выполняется, то отсюда s≤ или
-s≥-
или
-s≥- (3);
кроме того S≥
(3);
кроме того S≥ (4)
из (3) + (4) =>
(4)
из (3) + (4) =>
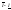 ≤S-s
=>(т.к. выполняется условие (3) =>
≤S-s
=>(т.к. выполняется условие (3) =>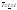 =>
s≤I≤S(5)
=> 0≤I-s≤S-s=>0≤S-I≤s-S,
т.к. I≥S
=>
=>
s≤I≤S(5)
=> 0≤I-s≤S-s=>0≤S-I≤s-S,
т.к. I≥S
=>
 =>
это означает, что
=>
это означает, что
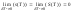 ;
;
 T:s≤σ≤S
=>
T:s≤σ≤S
=>
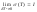 f(x)
интегрируема на [a;b]
f(x)
интегрируема на [a;b] (Mi-mi)Δxi=
(Mi-mi)Δxi= ωiΔxi;i=1,…,n,
чтобы функция была интегрируема,
необходимо и достаточно, чтобы
ωiΔxi;i=1,…,n,
чтобы функция была интегрируема,
необходимо и достаточно, чтобы
 ωiΔxi<ε
ωiΔxi<ε ε>0
ε>0
 δ(ε)>0
δ(ε)>0
 [c;d]<[a;b]=>l=d-c<δ=>ω<ε
[c;d]<[a;b]=>l=d-c<δ=>ω<ε ε>0
δ(ε)>0
ε>0
δ(ε)>0
 T:δT<δ
и
T:δT<δ
и
 i:ωi<
i:ωi<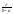 ;
S-s=
;
S-s= ωiΔxi<
ωiΔxi<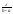 *
* Δxi=ε
=.> функция интегрируема.
Δxi=ε
=.> функция интегрируема.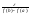 ,
тогда S-s=
,
тогда S-s= ,
,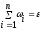 .
Для возрастающей функции доказательство
аналогично.
.
Для возрастающей функции доказательство
аналогично.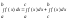
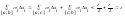 .
Следовательно f(x)
интегрируема на [a;b].
Докажем:
.
Следовательно f(x)
интегрируема на [a;b].
Докажем:
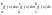 ;
;
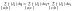 ;δT->0
;δT->0
 [a;b]
a<b<c;
[a;b]
a<b<c;
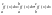 ;
;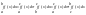
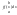 ≥0
≥0 ,
то и её предел≥0
,
то и её предел≥0
 ,
то и её предел ≥0
,
то и её предел ≥0
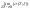 =
I<0;є=|ξ|;
|σ-I|<|I|;
σ<|I|+I;σ<δ;
=
I<0;є=|ξ|;
|σ-I|<|I|;
σ<|I|+I;σ<δ;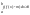 =>
=>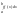 ≥
≥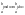 m(b-a);
m(b-a);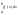 ≥
≥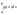

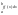 -
- ≥0
≥0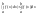 ;
;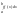 ≤
≤
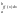 ≤
≤ ;|
;|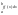 |<
|<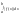 ;
Рассмотрим:
-A≤B≤A;
;
Рассмотрим:
-A≤B≤A;
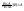
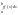 |≤|
|≤|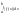 |
или a<b,
то если же a>b,
то |
|
или a<b,
то если же a>b,
то | |=|
|=|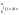 |≤
|≤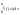 =|
=|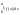 |=|
|=|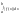 |
| ≤
≤ ≤M
≤M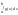
 xє[a;b];
mg(x)≤f(x)g(x)≤Mg(x)
xє[a;b];
mg(x)≤f(x)g(x)≤Mg(x) xє[a;b]
имеет смысл интеграл F(x)=
ax(f(t))dt
.
xє[a;b]
имеет смысл интеграл F(x)=
ax(f(t))dt
.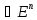 заданы непрерывно дифференцируемые
функции:
заданы непрерывно дифференцируемые
функции: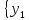 =
=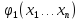 …
…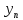 =
=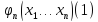 ,
тогда если
,
тогда если
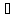 открытое множество D
в пространстве
открытое множество D
в пространстве
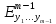 и
и
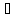 непрерывно дифференцируемая функция
непрерывно дифференцируемая функция
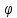 (
(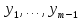 )
такая, что для любой точки x,
принадлежащей
G,
выполняются условия: 1) (
)
такая, что для любой точки x,
принадлежащей
G,
выполняются условия: 1) (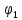 (x,…,
(x,…,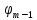 (x))
(x)) D.
2)
D.
2)
 (x),…
(x),…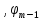 (x))=
(x))=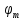 (x),
где
(x),
где
 зависимая
на множестве G
от функций
зависимая
на множестве G
от функций
 .
. =
=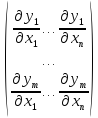 (2)
(2)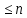 ,
постепенно функция (1) зависима на
открытом множестве G,
тогда в любой точке этого множества
ранг матрицы Якоби (2) этой системы
,
постепенно функция (1) зависима на
открытом множестве G,
тогда в любой точке этого множества
ранг матрицы Якоби (2) этой системы
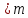 (Rg
(Rg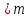 ).
).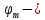 зависимая
на множестве G
от функций
зависимая
на множестве G
от функций
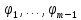 .
. (y1,...,yn)/
(y1,...,yn)/ (x1,...,xn)
= 0 во всех точках множества G.
(x1,...,xn)
= 0 во всех точках множества G. n
и пусть Rg(2)
хотя бы в одной точке множества G
равен m.
Тогда система (1) независима на множестве
G.
n
и пусть Rg(2)
хотя бы в одной точке множества G
равен m.
Тогда система (1) независима на множестве
G.