Логинов а.С. Часть 1. Дифференциальное исчисление Глава 1. Ведение

Операции над графиками

1.1. Некоторые понятия теории множеств и математической логики

В разделе рассматриваются основные понятия теории множеств, определение множества действительных чисел. Приводится необходимая терминология математической логики.

1.1.1. Множество, операции над множествами, обозначения

Множество - совокупность некоторых различимых объектов. Задать множество - задать признаки, характеризующие эти объекты.

Примеры:

N - натуральные числа, Z - целые числа, Q - рациональные числа, R - вещественные числа, [a,b] – отрезок, (a, b) – интервал, (a,b],[a,b) – полуинтервалы.

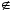Элемент принадлежит множеству x E, элемент не принадлежит множеству x E.

Подмножество A  E.

- пустое множество EE.

Обозначение множества перечислением - {a, b, c}.

Обозначение множества указанием характеризующего свойства – { x : x удовлетворет свойству P}.

Пример: N={xZ: x > 0}; [a,b]={x: axb}

Дополнение множества A (или разность двух множеств)

E\A={xE: xA}

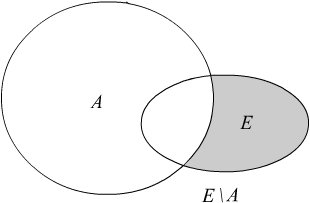
Рис. 1.1

Пересечение двух множеств AB ={x: xA и xB}

Рис. 1.2

Если два множества не пересекаются, то это можно записать в виде AB=.

Объединение двух множеств AB ={x: xA или xB}

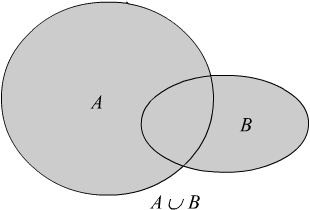
Рис. 1.3

Основные операции над множествами

Произведение множеств AB ={(x,y): xA и yB}.

Произведение множеств

Пример R² = R  R - плоскость.

1.1.2. Отображение, взаимно-однозначное соответствие, счетное и несчетное множества

Даны множества A и B. Отображение из A в B (или функция определенная на A со значениями в B) - соответствие или закон (обозначим его f ), которое каждому a A сопоставляет единственное b  B. Обозначения: A 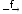B, f: A  B, b=f(a).

a - прообраз, b - образ при отображении f.

Отображение из A в B называется взаимно-однозначным, если

1) разные элементы из A имеют разные образы,

2) каждый элемент из B является образом некоторого элемента из A.

Эквивалентные множества A  B или множества одинаковой мощности, если существует взаимно-однозначное соответствие между элементами этих множеств.

Счетное множество A  N.

Пример: Множество рациональных чисел счетно.

Одно из важных свойств счетных множеств:

Объединение конечного или счетного числа счетных множеств является счетным множеством.

Несчетные множества. Бесконечное множество, не являющееся счетным, называется несчетным. Множество [0,1] имеет большую мощность, чем N. Множество эквивалентные по мощности отрезку [0,1] называются множествами мощности континуума. Множество действительных чисел R - несчетное множество, это множество является множеством мощности континуума.

1.1.3.Некоторые понятия математической логики (Дж. Маллас Пролог)

Примеры:

	Квантор	Субъект	Связка	Предикат
1	Все	числа	являются	не рациональными
2	Некоторые	натуральные числа	-	четны

В последнем случае подразумевается связка “являются”. Вместо термина предикат мы будем использовать также термин свойство. Суждения бывают истинными или ложными. Противоположное свойство P или отрицание свойства P обозначается значком 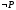или .

В традиционной логике допускаются два типа суждений, каждый из которых характеризует возможные отношения между двумя классами (классом субъектов и классом предикатов):

Все S являются P (каждый из S удовлетворяет свойству P)

Некоторые из S являются P ( существует представитель из S, удовлетворяющий свойству P )

Здесь S обозначает класс субъектов, а P - класс предикатов (или некоторое свойство, характеризующее этот класс ). Все, каждый, любой, произвольный называются универсальным квантором или квантором общности. Квантор общности обозначается значком . Некоторые из, существует - экзистенциальные кванторы. Квантор существования обозначается значком . Таким образом, основные типы суждений можно записать в следующей форме (логической связке соответствует символ двоеточия ):

1. xS: P (для любого x из S выполнено свойство P).

2. xS: P (существует x из S, для которого выполнено свойство P).

Предикат и субъект в суждении могут быть составными, в частности они сами могут быть суждениями. Например, рассмотрим высказывание (суждение):

 > 0  > 0 x,|x - x₀|< : | f(x) – 2 |< .

Это высказывание следует читать так: Для любого эпсилон больше нуля существует дельта больше нуля, (что) для всех икс, удовлетворяющих неравенству |x - x₀|< , выполнено неравенство 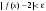. Это суждение является составным и может быть разложено на простейшие суждения следующим образом:

S₁ : P₁, где S₁ - класс субъектов, именно: S₁={xR,x > 0}, P₁ - предикат,

P₁=(S₂ : P₂), где S₂=S₁, P₂ - предикат,

P₂=(xS₃: P₃), S₃= S₃()={xR:|x - x₀|<}, P₃ – предикат (свойство) |f(x)-2|<.

Прямая и обратная теоремы, эквивалентность, метод математической индукции

Структура простейшей теоремы выглядит следующем образом: дано свойство A (условие), из него выводится свойство B (заключение).

В этом случае говорят A влечет B (из A следует B) и пишут A B . Последняя запись подразумевает, на самом деле, истинность выражения A B.

Если к тому же B 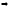A, то говорят, что верна и обратная теорема и пишут A B, при этом A и B называются эквивалентными.

Теорема. Отрицание суждения должно строиться по следующим формальным правилам:

1. квантор  заменяется на квантор .

2. квантор  заменяется на квантор .

3. предикат P заменяется на свое отрицание.

Пример:  >0  >0 x,|x - x₀|< : |f(x)-2| < .

его отрицание  >0  >0 x,|x - x₀|< : |f(x)-2|  .

Доказательство достаточно провести для двух типов простейших суждений:

1.  x: P.

2.  x: P.

Для таких суждений сформулированная теорема достаточно очевидна. Например, для первого суждения. Если для любого x выплнено P , то отрицанием будет: найдется x для которого P не будет выполнено. Это означает, что 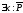. Если эта теорема доказана для простейших суждений 1 и 2, то остается еще раз заметить, что любое суждение можно представить, как составное и последовательно применять доказанное утверждение для простейших суждений, составляющих данное суждение.

Метод математической индукции

Имеется последовательность свойств P_n. Если доказано свойство P₁ и для всех k:

P_k 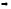P_k+1, то свойства P_n справедливы для всех n N.