Принцип двойственности

Пусть на P₂ фиксирован репер R(Е₁ , Е₂ , Е₃ , Е), пусть даны какие-либо точка А и прямая и (и₁ : и₂ : и₃).

Рассмотрим отображение f : P₂ → P₂ такое, что точке в соответствие ставится прямая с такими же координатами, а прямой – точка:

А → f (А)=а ( а₁ : а₂ : а₃) и и( и₁ : и₂ : и₃) → f (и) = .

Определение: Такое отображение называется корреляция.

Свойства:

1. А≠В f (А) ≠ f (В)

2. f ^-1.

Теорема. Корреляция сохраняет отношение принадлежности.

Доказательство. Докажем, что Аи f (и)f (А).

Пусть А и прямая и ( и₁ : и₂ : и₃), т.е. и₁ х₁ + и₂ х₂ + и₃ х₃ = 0.

Если Аи и₁ а₁ + и₂ а₂ + и₃ а₃ = 0.

f (А)=а ( а₁ : а₂ : а₃), значит а₁ х₁ + а₂ х₂ + а₃ х₃ = 0.

f (и) = U и f (и) f (А) а₁ и₁ + а₂ и₂ + а₃ и₃ = 0.

Очевидно, что эти условия одинаковы. □

Замечание: Таких отображений может быть много, они зависят от репера.

Замечание: В дальнейшем вместо термина «принадлежность» будем применять термин «инцидентность».

Примеры: «точка принадлежит прямой» ↔ «точка инцидентна прямой», или «прямая проходит через точку» ↔ «прямая инцидентна точке», или «две прямые пересекаются в одной точке» ↔ «две прямые инцидентны одной точке»

Вывод: Точки и прямые ведут себя одинаково.

Таким образом, можем сформулировать следующий принцип.

Малый принцип двойственности: Пусть верно некоторое предложение, касающееся точек и прямых и отношения инцидентности на проективной плоскости Р₂ , тогда будет верным предложение в котором слово «точка» заменено на слово «прямая», слово «прямая» заменено на слово «точка», отношение инцидентности не меняется.

Это принцип справедлив в силу свойств заданного выше отображения и теоремы. Вспомним свойства проективного пространства.

• Через две точки проходит одна прямая - Двум точкам инцидентна одна прямая.

• Две прямые пересекаются в одной точке - Двум прямым инцидентна одна точка.

Такие предложения называются двойственными.

Двойственными могут быть фигуры на проективной плоскости.

Определение: Фигура, состоящая из трёх различных точек, не лежащих на одной прямой и трёх прямых, проходящих через эти точки, называется трёхвершинником. Точки называются вершинами, а прямые сторонами.

Замечание: На расширенной евклидовой плоскости трёхвершинник может иметь несобственные точки. (Сколько?).

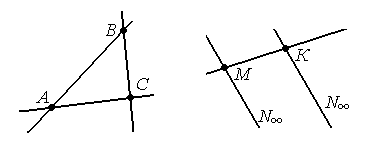
Обозначение: ∆АВС или ∆МКN_∞ .

Двойственной фигурой будет фигура, состоящая из трёх различных прямых не инцидентных одной точке и трёх точек не лежащих на одной прямой. Такую фигуру можно назвать трёхсторонником, но она состоит из тех же элементов что и трёхвершинник. Поэтому трёхвершинник считается фигурой, двойственной самой себе и термин «трехсторонник» обычно не применяют.

Определение: Фигура, состоящая из четырёх различных точек, среди которых никакие три не лежат на одной прямой и шести прямых, проходящих через эти точки, называется четырёхвершинником.

Замечание: На расширенной евклидовой плоскости четырёхвершинник может иметь несобственные точки. (Сколько?).

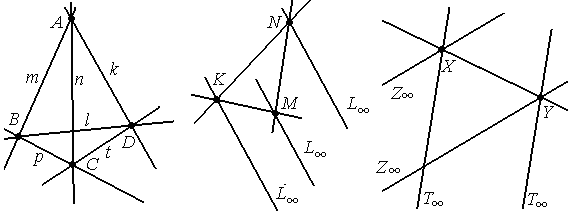
Обозначение: АВСD, или МКNL_∞ , или ХYZ_∞T_∞ .

Рассмотрим четырёхвершинник АВСD. Точки А, В, С, D – вершины, прямые (АВ), (АС), (АD), (ВС), (ВD), (СD) - стороны.

Определение: Стороны, не имеющие общих вершин, называются противоположными: (АВ) и (СD), (АС) и (ВD), (АD) и (ВС) – пары противоположных сторон.

Определение: Точки пересечения противоположных сторон называются диагональными точками

Определение: Трёхвершинник, составленный из диагональных точек называется диагональным трёхвершинником, а его стороны называются диагоналями.

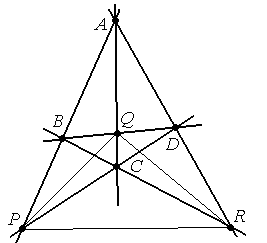
Например, четырёхвершинник АВСD

(АВ)∩(СD)=Р,

(АС)∩(ВD)=Q,

(АD)∩(ВС)=R,

∆PQR - диагональный трёхвершинник, а прямые (PQ), (PR), (QR) – диагонали.

Четырехвершинники МКNL_∞ и ХYZ_∞T_∞ :

Двойственной фигурой будет фигура, состоящая из четырёх различных прямых среди которых никакие три не инцидентны одному пучку и шести точек пересечения этих прямых. Такую фигуру называют четырёхсторонником.

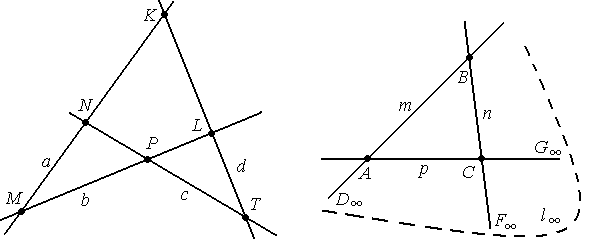
Обозначение: abcd или mnpl_∞