Аналитическое представление проективных преобразований

Любое проективное преобразование однозначно определяется парой реперов R(Е₁ , Е₂ , Е₃ , Е) и R′(Е′₁ , Е′₂ , Е′₃ , Е′). Так как реперы заданы, тогда можно найти преобразование координат при переходе от одного репера к другому, т.е. можно найти матрицу А причем она не вырождена (почему?).

Формулы преобразования координат одной и той же точки Х будут:

λ Х_R =A∙X_R′ и μ X_R′ = А^-1 ∙ Х_R (*)

Пусть f (Х) = Х ', причем Х_R и Х '_R′ .

Найдем координаты точки Х ' в репере R: λ Х '_R = A∙Х '_R′ .

Таким образом, λ Х '_R =A∙Х_R , тогда μ Х = A^-1 ∙f (Х) (**)

(Почему существует обратная матрица?)

Замечание: Хотя формулы (*) и (**) вроде бы одинаковые, необходимо помнить, что в (*) одна и та же точка в разных реперах, в (**) две разные точки (образ и прообраз) в одном репере.

Матрица, задающая преобразование координат для двух данных реперов R(Е₁ , Е₂ , Е₃ , Е) и R′(Е′₁ , Е′₂ , Е′₃ , Е′) единственна (с точностью до пропорциональности). Отсюда следует, что проективное преобразование задает единственную матрицу A (с точностью до пропорциональности).

Теорема. Если на Р₂ задано отображение формулами (**), тогда это отображение является проективным преобразованием.

Доказательство. Пусть f : Р₂ → Р₂ , так что λ f (Х)= A∙Х.

Рассмотрим точки репера Е₁ , Е₂ , Е₃ , Е , их образы обозначим

Е′₁ , Е′₂ , Е′₃ , Е′. Необходимо и достаточно доказать что точки

Е′₁ , Е′₂ , Е′₃ , Е′ образуют новый репер (т.е никакие три не лежат на одной прямой и он согласован).

Пусть матрица A =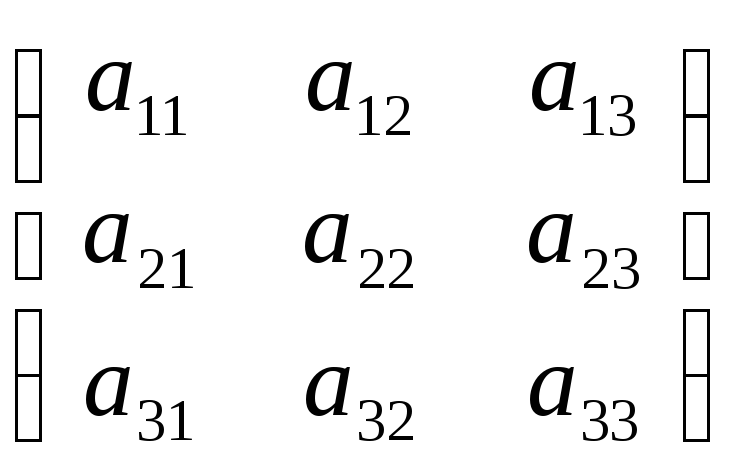, тогда Е′₁= f (Е₁)= A· = ,

Е′₂= f (Е₂)= A· = , Е′₃=f(Е₃)=A· = , Е′=f(Е)=A· =

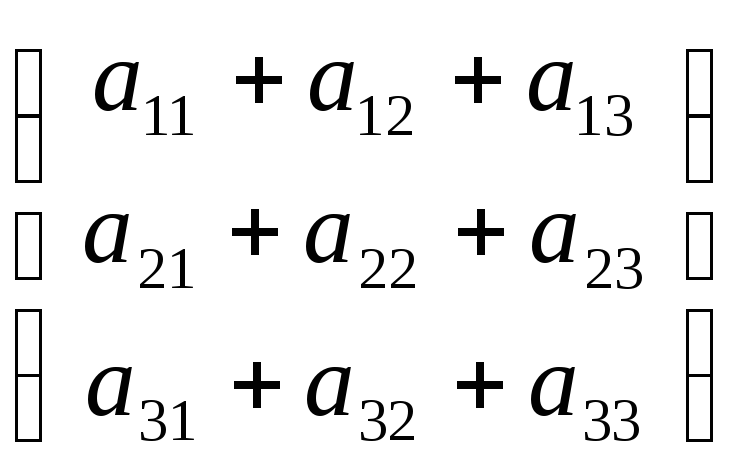
Е′₁ , Е′₂ , Е′₃ - не лежат на одной прямой, так как ≠0 (почему?),

То же самое можно сказать о тройках: Е′₁ , Е′₂ , Е′, Е′₁ , Е′₃ , Е′, Е′₂ , Е′₃ , Е′.

Т.к., Е′₁ + Е′₂+ Е′₃= Е′ - есть согласованность (проверьте).

Таким образом, f : R(Е₁ , Е₂ , Е₃ , Е) → R′(Е′₁ , Е′₂ , Е′₃ , Е′), а значит f - есть проективное преобразование. □

Вывод: Проективное преобразование однозначно определяется формулами (**), то есть матрицей A. Поэтому это тоже можно считать определением проективного преобразования.

Определение: Композицией двух проективных преобразований f : Х → Х′ и g : Х′ → Х′′ будем называть последовательное выполнение преобразований сначала f затем g.

Обозначение: f ◦ g

При этом f : R → R′ и g : R′ → R′′ , значит f ◦ g : R → R′′, т.о., f◦g - проективное преобразование.

(почему?).

Пусть f задается матрицей A, а g задается матрицей В.

Т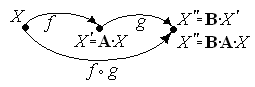огда f◦g(Х)=f(g(Х))=f(A·Х)=В(A·Х)=В·A·Х,

таким образом матрицей преобразования f◦g является матрица В·A, причем она не вырождена. (почему?).

Определение: Преобразование, оставляющее все точки плоскости на месте, называется тождественным.

Тождественное преобразование задается матрицей – Е.

Определение: Обратным преобразованием для f : Х → Х′ будет преобразование f ^-1 : Х′ → Х .

Если f : R → R′ ,

тогда f ^-1 : R′ → R.

f ^-1 - проективное преобразование (почему?).

f ^-1 будет задаваться - А^-1 (почему?).

Теорема. Множество П - проективных преобразований является группой относительно операции композиция.

Доказательство. Самостоятельно.

Теорема. Проективное преобразование прямой образует подгруппу в группе проективных преобразований - П.

Доказательство. Самостоятельно.

Виды проективных преобразований:

1. Инволюция – нетождественное проективное преобразование , совпадающее со своим обратным: f = f ^-1.

2. Коллинеация - проективное преобразование, при котором прямая переходит в прямую, точка переходит в точку.

3. Корреляция - проективное преобразование, при котором прямая переходит в точку, точка переходит в прямую.

4. Гомология - проективное преобразование, имеющее по крайней мере три неподвижных точки принадлежащие одной прямой.

5. Центральное проектирование.

Множество коллинеаций образует подгруппу в группе проективных преобразований. Подгруппа коллинеаций сама имеет несколько подгрупп. Эта идея («групповая») была положена в основу классификации геометрических преобразований Феликсом Клейном в 1872 году в работе «Сравнительное обозрение новейших геометрических исследований». Другое название этой работы - «Эрлангенская программа».

Геометрия – это учение о геометрических преобразованиях и каждая геометрия характеризуется соответствующей группой преобразований. Предметом геометрии являются те свойства фигур, которые инвариантны при преобразованиях данной группы.

Евклидова геометрия изучает те свойства фигур, которые сохраняются при движениях - Д (длины, углы). Аффинная геометрия изучает те свойства фигур, которые сохраняются при аффинных преобразованиях - А (простое отношение точек, параллельность прямых). Проективная геометрия изучает те свойства фигур, которые сохраняются при проективных преобразованиях - П (сложное отношение точек, инцидентность, точка, прямая, пучок, репер, квадрики).

Д А П