
- •Аналитическое представление проективных преобразований 71
- •Дополнительная литература 91 введение
- •Структурно-логическая схема курса «проективная геометрия»
- •Исторические сведения
- •Проективное пространство
- •Аксиомы проективного пространства
- •Модели проективной прямой, проективной плоскости
- •Изоморфизм моделей
- •Проективная система координат
- •Проективный репер
- •Координаты точки на прямой (плоскости)
- •Принадлежность трёх точек одной прямой
- •Однородные проективные координаты
- •Уравнение прямой. Координаты прямой
- •Взаимное расположение двух прямых
- •Принадлежность трёх прямых одному пучку
- •Координаты точки и уравнение прямой в пространстве
- •Преобразование координат
- •Принцип двойственности
- •Теорема Дезарга
- •Простое отношение
- •Сложное отношение
- •Гармонизм
- •Гармонические свойства полного четырехвершинника
- •Квадрики на проективной плоскости
- •Классификация кривых второго порядка на проективной плоскости.
- •Взаимное расположение прямой и квадрики
- •Уравнение касательной
- •Полюс и поляра
- •Теорема Штейнера
- •Теорема Паскаля и ее предельные случаи
- •Задачи на построение, связанные с овалом
- •Прямые и квадрики на расширенной евклидовой плоскости
- •Проективные преобразования
- •Проективные преобразования плоскости
- •Аналитическое представление проективных преобразований
- •Перспектива
- •Отображение пучка в пучок
- •Инволюция
- •Коллинеация
- •Инварианты коллинеации
- •Гомология
- •Гомологии на расширенной плоскости
- •Дополнительная литература
Полюс и поляра
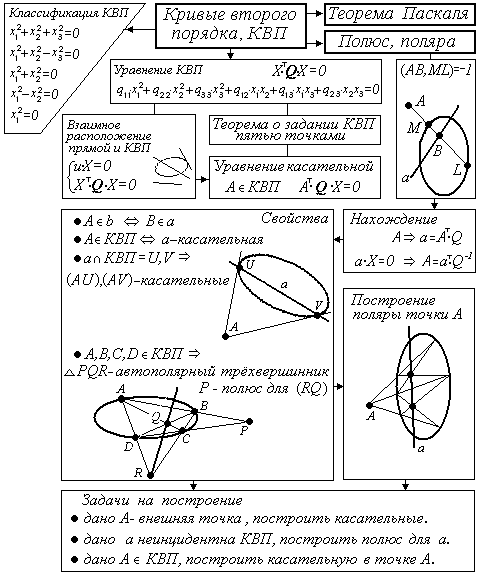
Рассмотрим овальную квадрику ХТ∙Q∙Х = 0 и точки А и В не принадлежащие квадрике.
П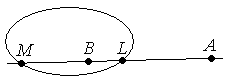 усть
M
и L
точки пересечения квадрики и прямой
(АВ).
усть
M
и L
точки пересечения квадрики и прямой
(АВ).
Определение: Если (AB,ML)=-1, то говорят что овальная квадрика гармонически разделяет пару АВ, или точки А и В гармонически сопряжены относительно овальной квадрики.
На прямой (АВ)
рассмотрим репер R(A,B,M),
тогда в этом репере и точки А![]() ,
В
,
В
![]() ,
М
,
М
![]() и пусть
точка L
и пусть
точка L
![]() .
.
Если (AB,ML)=
-1, тогда ![]() =
-1
=
-1 ![]() α
= 1 и β
= -1 , т.е. L
α
= 1 и β
= -1 , т.е. L
![]() .
.
Таким образом, М = А+В и L = А – В.
Значит, для точек
пересечения прямой (АВ)
с квадрикой
![]() .
.
Но
![]() являются корнями уравнения λ²∙а
+ 2∙λ∙μ∙с
+ μ²∙b=0,
являются корнями уравнения λ²∙а
+ 2∙λ∙μ∙с
+ μ²∙b=0,
где а = АТ∙Q∙А, b = ВТ∙Q∙В, с = А Т∙Q∙В = ВТ∙Q∙А.
По теореме Виета
сумма корней равна среднему коэффициенту,
взятому с противоположным знаком:
![]() +
+![]() =
- с
=
- с
![]() с = 0
с = 0
![]() АТ∙Q∙В
= ВТ∙Q∙А
= 0 - условие
гармонической сопряженности точек А
и В
относительно квадрики.
АТ∙Q∙В
= ВТ∙Q∙А
= 0 - условие
гармонической сопряженности точек А
и В
относительно квадрики.
Фиксируем точку
А
![]() КВП. Рассмотрим все прямые проходящие
через эту точку в каждом случае будет
своя точка В
гармонически сопряженная с А
относительно овальной квадрики. Сделаем
точку В
переменной, по условию гармонической
сопряженности точек относительно
овальной квадрики получим: АТ∙Q∙Х
= 0
- это уравнение I степени, то есть прямая,
причем это прямая единственна. Эту
прямую будем называть полярой точки
А.
Если точка А
КВП. Рассмотрим все прямые проходящие
через эту точку в каждом случае будет
своя точка В
гармонически сопряженная с А
относительно овальной квадрики. Сделаем
точку В
переменной, по условию гармонической
сопряженности точек относительно
овальной квадрики получим: АТ∙Q∙Х
= 0
- это уравнение I степени, то есть прямая,
причем это прямая единственна. Эту
прямую будем называть полярой точки
А.
Если точка А
![]() КВП, то уравнение АТ∙Q∙Х
= 0
определяет касательную к квадрике в
точке А.
КВП, то уравнение АТ∙Q∙Х
= 0
определяет касательную к квадрике в
точке А.
Определение: Полярой точки А называется прямая, состоящая из точек гармонически сопряженных с данной точкой относительно овальной квадрики.
Вывод: Полярой точки А является прямая, которая имеет уравнение: АТ∙Q∙Х = 0 и
в случае А
![]() КВП является касательной к овальной
квадрике,
КВП является касательной к овальной
квадрике,
в случае А
![]() КВП состоит из точек гармонически
сопряженных с точкой А
относительно овальной квадрики.
КВП состоит из точек гармонически
сопряженных с точкой А
относительно овальной квадрики.

Определение: Уравнение АТ∙Q∙Х = 0 называется уравнением поляры точки А относительно овальной квадрики.
Если уравнение прямой а∙Х=0, тогда λ∙а = АТ∙Q (с точностью до пропорциональности).
λ∙а
= АТ∙Q
![]() λ∙а∙Q-1
= АТ∙Q∙Q-1
λ∙а∙Q-1
= АТ∙Q∙Q-1
![]() μ∙АТ=
а∙Q-1
или μ∙А=
Q-1
∙аТ
μ∙АТ=
а∙Q-1
или μ∙А=
Q-1
∙аТ
(Почему существует Q-1 и почему (Q-1)Т= Q-1 ? )
Вывод: Для любой прямой существует точка, для которой эта прямая является полярой относительно квадрики.
Определение: Точка, для которой данная прямая относительно овальной квадрики является полярой, называется полюсом прямой.
Свойства:
1. Если точка А внешняя по отношению к овальной квадрике, то ее поляра проходит через точки касания касательных проведенных из точка А к КВП.
Доказательство.
Координаты точек касания Х1
и Х2
находятся из системы
 ,
первое уравнение это уравнение квадрики,
второе уравнение это уравнение поляры,
а значит это точки пересечения поляры
и квадрики. □
,
первое уравнение это уравнение квадрики,
второе уравнение это уравнение поляры,
а значит это точки пересечения поляры
и квадрики. □
2. Если точка и прямая инцидентны, то их поляра и полюс тоже инцидентны.
Доказательство. Пусть а – поляра точки А и В - полюс прямой b,
значит λ∙а
= АТ∙Q
и μ∙В=
Q-1
∙bТ. Докажем,
что А
![]() b
b
![]() B
B
![]() a.
a.
Уравнение прямой
b∙Х
= 0, тогда А
![]() b
b
![]() b∙А
=0.
b∙А
=0.
Найдем а∙В=(АТ∙Q)∙(Q-1∙b)=АТ∙(Q∙Q-1)∙bТ=АТ∙Е∙bТ=АТ∙bТ=(А∙b)Т=0 - это означает, что точка В лежит на прямой а. □
Замечание: Свойство 2 позволяет находить полюс прямой. Выбрав на данной прямой две любые точки и построив их поляры, точка их пересечения будет полюсом данной прямой.
Задача.
Дана квадрика х1²
- 2∙х2²+
4∙х2∙х3
=0 . Найти уравнение поляры для А![]() и координаты полюса прямой b:
х1+х2–2∙х3=0.
и координаты полюса прямой b:
х1+х2–2∙х3=0.
Решение. Q=
![]() Q-1=
Q-1=
λ∙а=АТ∙Q=(
1: 3 :-1) ∙ =(1
:-8: 6)
=(1
:-8: 6)
![]() х1
-8∙х2+6∙х3=0.
х1
-8∙х2+6∙х3=0.
μ∙В=Q-1∙bТ= ∙
∙![]() =
=
![]() В=
В=![]() .
.
Задача.
Дана квадрика 2∙х1²
+ х3²
- 2∙х1∙х2
-2∙х1∙х3
=0 . Найти уравнения касательных к квадрике
из точки А![]() .
.
Решение.
Воспользуемся свойством (1). Q= . Найдем
уравнение поляры.
. Найдем
уравнение поляры.
λ∙а
= АТ∙Q=(
1: 8 : 5 )∙ =(
-11 : -1 : 4 )
=(
-11 : -1 : 4 )
![]() 11∙х1
+ х2
- 4∙х3
=0.
11∙х1
+ х2
- 4∙х3
=0.
Найдем точки пересечения квадрики поляры.

![]()
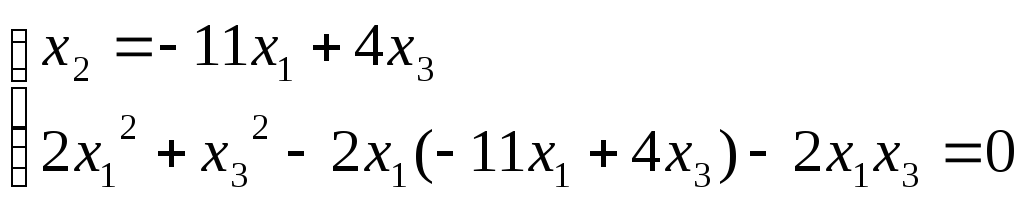
![]()
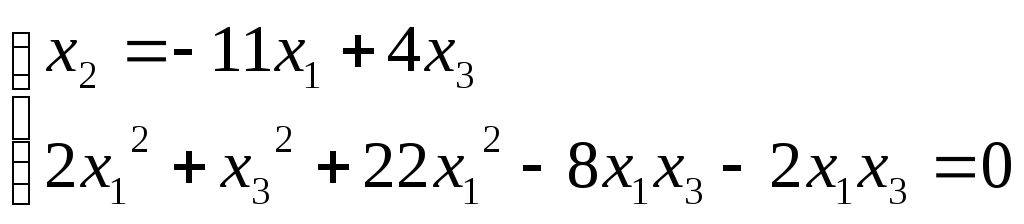
![]()
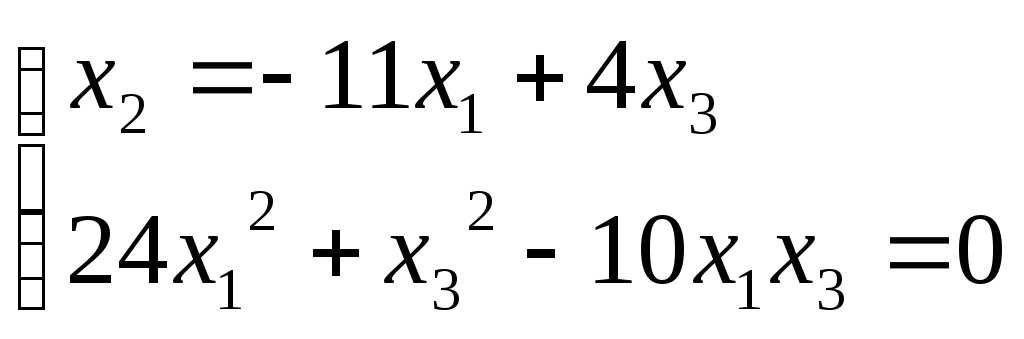
![]()
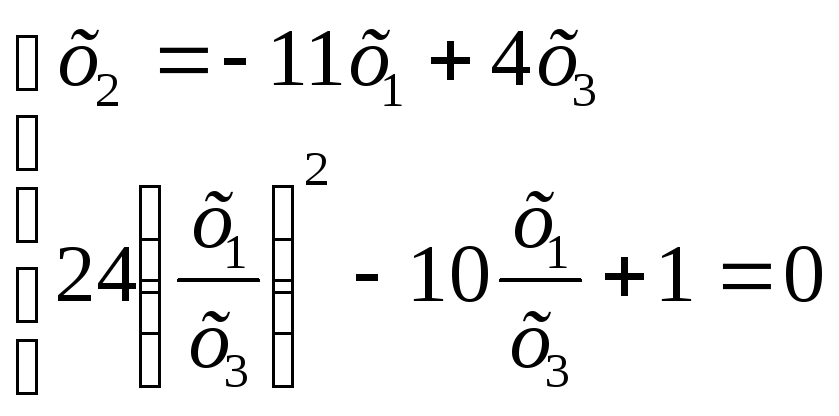
![]()
D=100–96
= 4 ![]()
![]() и
и
![]() .
.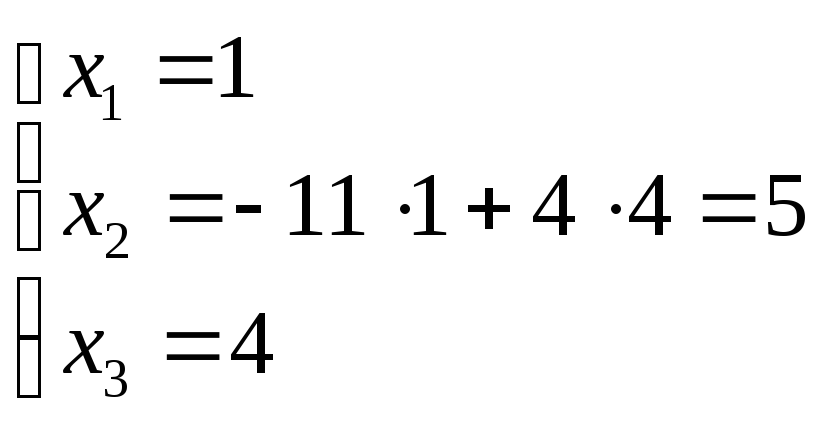 и
и
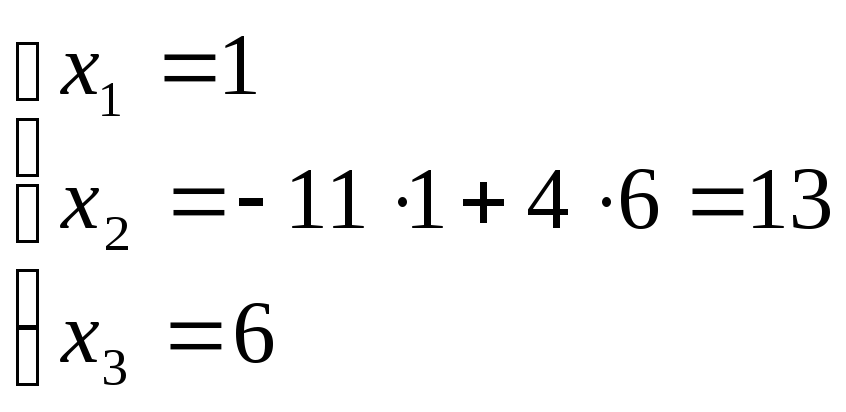
![]()
В![]() и С
и С![]() - точки пересечения поляры и квадрики,
тогда прямые (АВ)
и (АС)
будут касательными.
- точки пересечения поляры и квадрики,
тогда прямые (АВ)
и (АС)
будут касательными.
(АВ)
:
 =0
=0 ![]() -
7∙х1
- х2
+ 3∙х3
=0.
-
7∙х1
- х2
+ 3∙х3
=0.
(АС)
:
 =0
=0 ![]() 17∙х1
+ х2
-
5∙х3
=0.
17∙х1
+ х2
-
5∙х3
=0.
Определение: Трехвершинник называется автополярным относительно овальной квадрики, если каждая его вершина является полюсом противоположной стороны.
Замечание: Автополярных трехвершинников может быть много.
Теорема. Для того чтобы уравнение овальной квадрики было каноническим необходимо и достаточно, чтобы ΔЕ1Е2Е3 был автополярным относительно данной квадрики.
Доказательство. Необходимость:
Дано q11 ∙х1² + q22∙х2² + q33∙х3² =0 .
Доказать что ΔЕ1Е2Е3 автополярный трёхвершинник.
Достаточность: Найти матрицу Q , используя то, что точка Е1
является полюсом прямой (Е2Е3 ) и т.д. (самостоятельно).
Определение: Четырехвершинник называется вписанным в овальную квадрику, если его вершины инцидентны квадрике.
Теорема. Если четырехвершинник вписан в овальную квадрику, тогда диагональный трехвершинник является автополярным относительно квадрики.
Доказательство. Пусть АВСD – четырёхвершинник вписанный в овальную квадрику и ΔPQR - диагональный трёхвершинник.
Докажем, что Р - полюс прямой (QR).
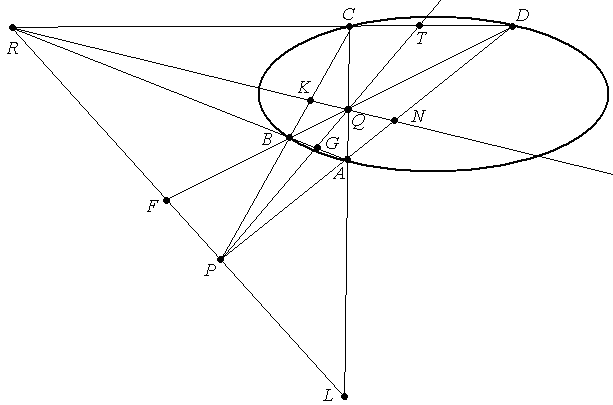
По гармоническим
свойствам полного четырехвершинника
гармоническими будут: (CB,PK)=(AD,PN)=
-1, т.е. точки K
и N
гармонически
сопряжены с точкой Р
относительно овальной квадрики, а значит
они принадлежат поляре точки Р.
В тоже время точки K
и N
лежат на
прямой (QR)
![]() (QR)
- поляра точки Р.
Для точек Q
и R
доказательство аналогично. □
(QR)
- поляра точки Р.
Для точек Q
и R
доказательство аналогично. □
Замечание: Эта теорема позволяет строить поляру точки если она не инцидентна овальной квадрике.
Задачи на построение
Задача 1. Дана овальная квадрика и точка Р ей не инцидентная. Построить поляру точки Р.
Решение. Пусть для определенности Р – внешняя точка. Необходимо восстановить какой-либо четырёхвершинник инцидентный овальной квадрике, так чтобы точка Р была одной из диагональных точек. Через точку P проводим две произвольные прямые а и b так чтобы они пересекали квадрику: а ∩ КВП =А, В, b ∩ КВП = С, D.
АВСD - является вписанным четырехвершинником и точка P является диагональной точкой. Строим две другие диагональные точки: (АС)∩(ВD)=Q, и (АD)∩(ВС)=R.
Прямая (RQ) является полярой.
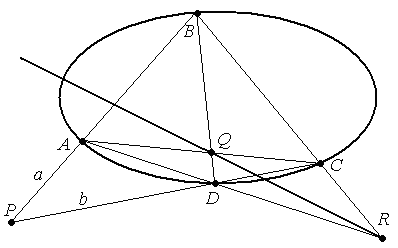
Замечание: В некоторых случаях одну из диагональных точек построить сложно, она может выйти за пределы чертежа. В этом случае можно построить ещё один какой-либо четырехвершинник вписанный в овальную квадрику.
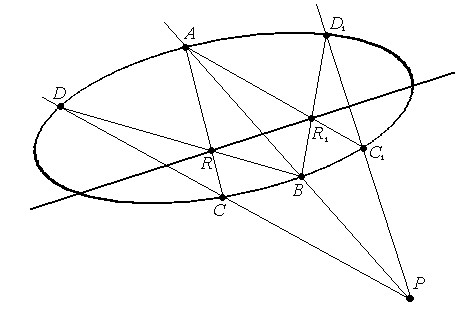
Замечание: Если P – внутренняя точка построение аналогичное.
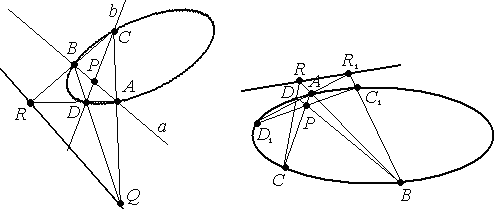
Задача 2. Дана овальная квадрика и прямая а. Построить полюс прямой.
Решение. Воспользуемся свойством (2).
На прямой а возьмем две различные точки В и С, построим их поляры - b и с (см. пред. задачу).
b ∩ с = А – полюс прямой а .
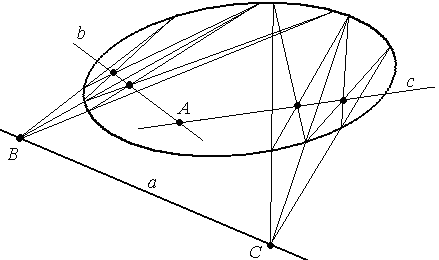
Задача 3. Дана овальная квадрика и точка А ей инцидентная, построить поляру точки.
Решение. Поляра точки в этом случае будет касательной.
Воспользуемся свойством (2): если через точку А провести какую-либо прямую b, то её полюс – В пройдет через поляру точки А.
Построение полюса прямой – задача 2.
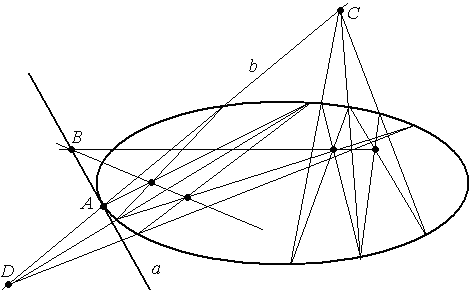
Задача 4. Дана овальная квадрика и точка А. Через точку А провести касательную к квадрике.
Решение.
1. А - внутренняя точка - касательных нет.
2 А
![]() КВП – касательная является полярой
(см. задачу 3).
КВП – касательная является полярой
(см. задачу 3).
3. А - внешняя точка - касательные две. По свойству (1), если а поляра точки А, тогда а ∩ КВП = В и С - эти точки являются точками касания. Т.е. (АВ) и (АС) - касательные.
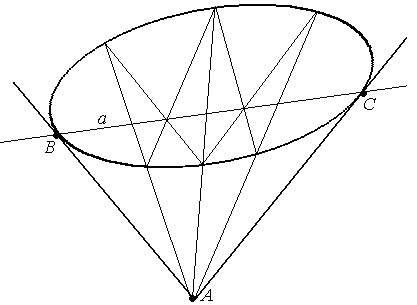
Задача 5. Дана овальная квадрика и прямая а , касающаяся квадрики, построить полюс прямой.
Р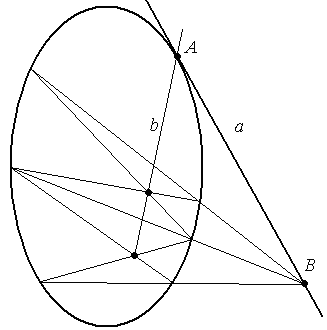 ешение.
Полюс прямой в этом случае будет точкой
касания.
ешение.
Полюс прямой в этом случае будет точкой
касания.
Воспользуемся свойством (2). Если на данной прямой а взять какую-либо точку В, то её поляра – b пройдет через полюс прямой а.
Построение поляры точки – задача 1.
