Теорема Штейнера

Теорема Штейнера. Рассмотрим на проективной плоскости два пучка П(О₁) и П(О₂), причем О₁ ≠ О₂. Если существует проективное, но не перспективное отображение f : П(О₁) → П(О₂), тогда множество точек пересечения соответствующих друг другу прямых пучков образует овальную квадрику проходящую через точки О₁ и О₂ . При этом касательная к квадрике в точке О₁ является прообразом прямой (О₁О₂), а касательная в точке О₂ является образом прямой (О₁О₂).

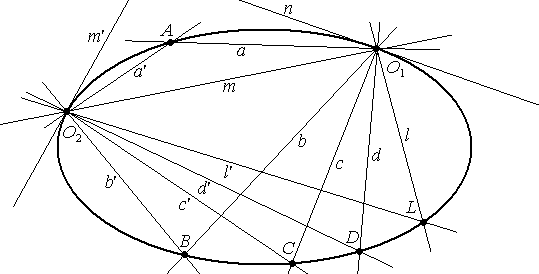
Доказательство. Пусть f - проективное, но не перспективное отображение пучка в пучок f : П(О₁) → П(О₂).

Обозначим: (О₁О₂)= т, т.к. f - не перспектива, то f (т) ≠ т и f ^-1(т) ≠ т.

Пусть: f (т)=т′ и f ^-1(т)=п, т.о. прямые т, т′, п - попарно различны.

f : п → т и f : т → т′ - две пары прямых есть, для задания отображения нужны три пары прямых. Возьмем ℓП(О₁) ( ℓ≠т и ℓ≠п ), пусть : f (ℓ)= ℓ′ О₁ = п ∩ т, О₂= т ∩ т′,

Пусть п ∩ т′= О₃, ℓ ∩ ℓ′=Е.

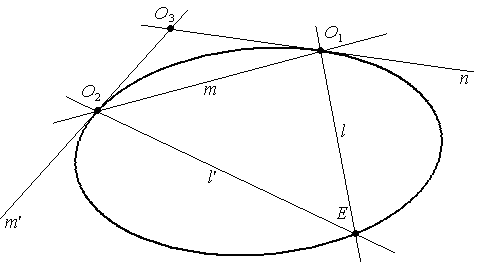
Все прямые попарно различны, значит точки не лежат на одной прямой. В этом случае точки могут образовывать репер на проективной плоскости: R (О₁ , О₂ , О₃ , Е)

П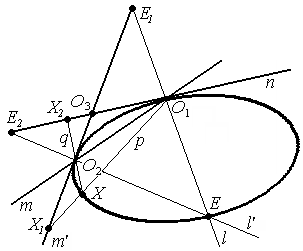усть Х произвольная точка на плоскости и ее координаты в этом репере.

Обозначим: (О₁ Х) = р, (О₂ Х) = q,

Е₁= ℓ ∩ т′, Е₂= п ∩ ℓ′, Х₁= р ∩ т′, Х₂= п ∩ q.

По определению сложного отношения прямых пучка:

для пучка П(О₁) → (тп,ℓр)=(О₂О₃,Е₁Х₁),

для П(О₂) → (т′т,ℓ′q)=(О₃О₁, Е₂Х₂).

Т.к. Е₁ и Х₁ – проекции точек Е и Х на (О₂О₃) , тогда по теореме о проекциях: Х₁ и в репере R (О₂ , О₃ , Е₁) → Х₁ (О₂О₃ , Е₁Х₁) = .

Так как Е₂ и Х₂ – проекции Е и Х на (О₁О₃) , тогда по теореме о проекциях:

Х₂ и в репере R (О₁ , О₃ , Е₁) → Х₂(О₁О₃ , Е₂Х₂) = .

Тогда (тп,ℓр)=(О₂О₃,Е₁Х₁)= , (т′т,ℓ′q)=(О₃О₁,Е₂Х₂)= .

Если точка Х является точкой пересечения соответствующих прямых пучков, то есть f (р) = q, тогда в силу проективности отображения f : (тп,ℓр)=(т′т,ℓ′q) =

х₃² - х₁∙х₂ = 0 – уравнение овальной квадрики, а значит точка Х принадлежит некоторой квадрике.

Если точка Х не является точкой пересечения соответствующих прямых пучков (f (р)≠q), тогда

(тп,ℓр)≠(т′т,ℓ′q) ≠ х₃² - х₁∙х₂ ≠ 0 , а значит, точка Х КВП.

Если точка Х инцидентна прямым (О₁О₂), (О₁О₃) или (О₂О₃), то для принадлежности квадрике она должна совпадать или с О₁ или с О₂ .

Найдем касательную к квадрике в точке О₁ .

Матрица квадрики Q = 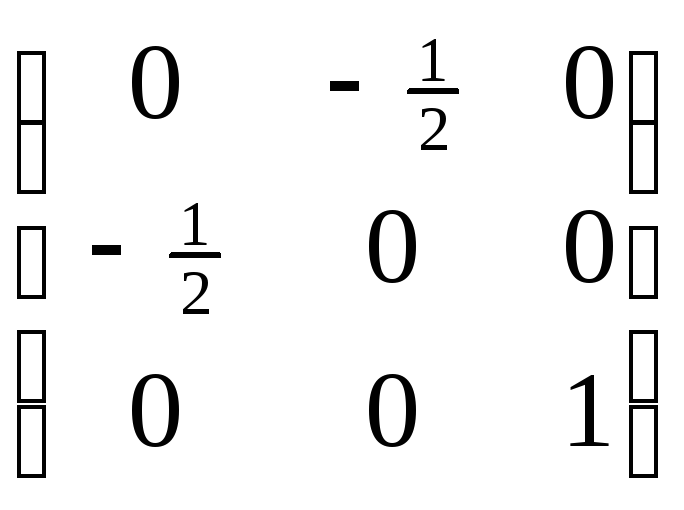. Касательная: О₁^Т ∙Q∙Х=0.

∙∙=0 ∙=0 х₂ = 0 – это уравнение координатной прямой (О₁О₃)= п .

Аналогично находится касательная в точке О₂ : х₁ = 0 – это уравнение (О₂О₃)= т′.

Т.о. при таком проективном отображении прообраз прямой (О₁О₂) является касательная в точке О₁ образом прямой (О₁О₂) является касательная в точке О₂. □

Обратная теорема. Пусть даны овальная квадрика и точки О₁, О₂ принадлежащие ей. Тогда для любой точки АКВП отображение f : П(О₁) → П(О₂), такое, что f : (АО₁) → (АО₂) - является проективным, но не перспективным отображением. Причем касательная к квадрике в точке О₁ является прообразом прямой (О₁О₂), а касательная в точке О₂ является образом прямой (О₁О₂).

Замечание: Если отображение f – перспектива, то все точки пересечения соответствующих прямых (образов и прообразов) лежат на одной прямой – оси перспективы. Прямая соединяющая центры пучков отображается сама в себя. Таким образом, квадрика является вырожденной - парой совпавших прямых (ось перспективы и прямая (О₁О₂)).

Вывод: Если дано проективное отображение f : П(О₁) → П(О₂), тогда множество точек пересечения соответствующих прямых пучков является КВП.

Если f : П(О₁) → П(О₂), - не перспективное отображение, то КВП овальная.

Если f : П(О₁) → П(О₂), - перспективное отображение, то КВП вырожденная.