Отображение пучка в пучок

Рассмотрим отображение двойственное перспективе прямой на прямую:

Определение: Перспективой пучка в пучок с осью s называется отображение φ : П(L₁) → П(L₂), при котором каждой прямой а₁ пучка П(L₁) ставится в соответствие прямая а₂ пучка П(L₂) такая что прямые а₁ и а₂ пересекаются в точке инцидентной оси s.

В силу принципа двойственности будут выполняться все свойства перспективы прямой на прямую (сформулировать самостоятельно).

Замечание: Перспектива пучка в пучок тоже является проективным преобразованием.

Теорема. Пусть даны два пучка П(L₁) и П(L₂). В каждом пучке отмечены три различные прямые а₁ , b₁ ,с₁ П(L₁) и а₂ , b₂ , с₂ П(L₂). тогда существует единственное проективное отображение f : П(L₁) → П(L₂), при котором прямые а₁ , b₁ ,с₁ переходят в прямые а₂ , b₂ , с₂.

Доказательство. Самостоятельно.

Построение перспективы пучка в пучок.

1 случай: П(L₁) ≠ П(L₂).

1. А = а₁ ∩ а₂ , через точку А проводим две прямые - s₁ и s₂

2. s₁∩b₁ =В₁ и s₁∩с₁ =С₁ .

3. s₂∩b₂ =В₂ и s₂∩с₂ =С₂ .

4. S =(В₁В₂)∩(С₁С₂).

5. Рассмотрим отображения φ₁ : П(L₁) → П(S) - перспектива с осью s₁ и φ₂ : П(S) → П(L₂) - перспектива с осью s₂ , тогда искомое проективное преобразование φ = φ₂ ◦ φ₁ . так как φ₁ и φ₂ - проективные преобразования, то φ - тоже проективное преобразование.

6. N₁ =п₁∩s₁ , N₂ =( N₁S)∩s₂ ,

7. (N₂L₂) - образ прямой п₁ .

2 случай: П(L₁) = П(L₂) рассмотреть самостоятельно.

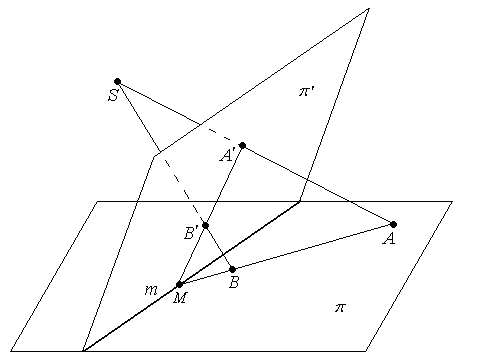
Определение: Центральной проекцией плоскости π на плоскость π' из точки S называется отображение при котором каждой точке А плоскости π ставится в соответствие точка А' плоскости π' такая что А'= π ' ∩ (SА).

Свойства:

Выполняются свойства 1 - 2 перспективы прямой на прямую.

3. При перспективе плоскости на плоскость прямая пересечения плоскостей переходит сама в себя.

Определение: Перспективой пучка в пучок в пространстве Р₃ с плоскостью перспективы π называется отображение φ : П(L₁) → П(L₂), при котором каждой прямой а₁ пучка П(L₁) ставится в соответствие прямая а₂ пучка П(L₂) такая что прямые а₁ и а₂ пересекаются в точке инцидентной плоскости перспективы π.

Инволюция

Определение: Нетождественное проективное преобразование, совпадающее со своим обратным называется инволюцией φ = φ ^-1.

Рассмотрим φ ◦ φ ^-1.

С одной стороны φ◦φ ^-1= е, с другой φ◦φ ^-1 = φ◦φ = φ², φ² = е.

φ³=φ◦φ² = φ◦е = φ , φ⁴ =φ◦φ³ = φ◦φ = φ² = е и т.д.

Замечание: В дальнейшем будем рассматривать инволюцию прямой.

Теорема. Для того чтобы преобразование прямой на себя было инволюцией необходимо и достаточно, чтобы на этой прямой существовала пара точек переходящих друг в друга: А ↔ А′.

Доказательство.

Необходимость: Дано φ=φ^-1 и А→φ(А)=А′. Доказать, что А′→ φ(А′)=А.

φ(А′) = φ(φ(А)) = φ◦φ (А) = е(А) = А .

Достаточность: Дано φ(А) = А′ и φ(А′) = А. Доказать , что φ = φ ^-1,

т.е. Х если φ (Х)= Х′ , то φ(Х′)= Х .

От противного. Пусть φ (Х)= Х′ , то φ(Х′)= Х ″ ≠ Х.

Так как это проективное преобразование, то сохраняется сложное отношение четырех точек (АА′,ХХ ′ )= (φ(А)φ(А′),φ(Х)φ(Х ′ ))= (А′А,Х ′ Х ′′ ) = (АА′,Х ′′ Х ′ ), то в силу свойств и единственности сложного отношения получим, что Х = Х ′′. □

Отображение прямой на себя будет задаваться невырожденной матрицей второго порядка.

Пусть М, если φ=φ^-1 , тогда М=М^-1 М²=λ∙Е.

=

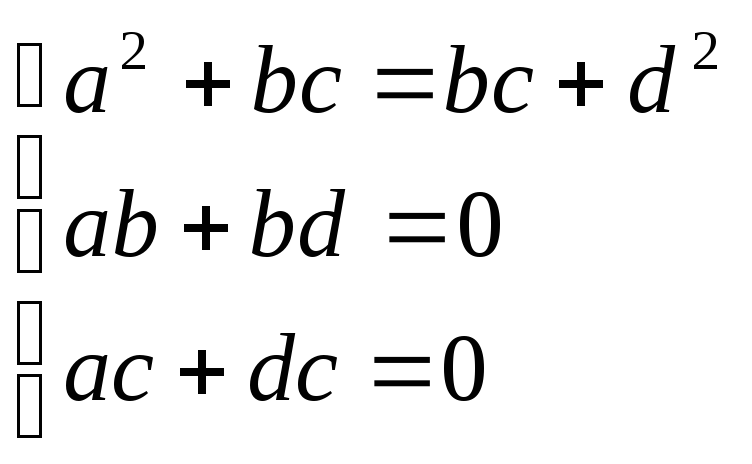
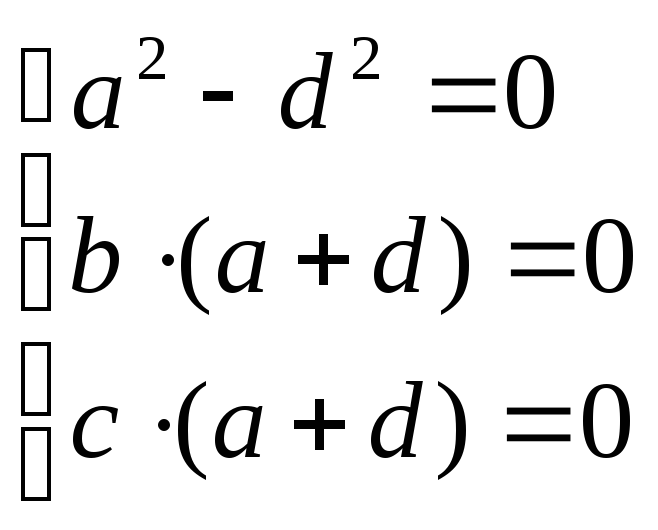
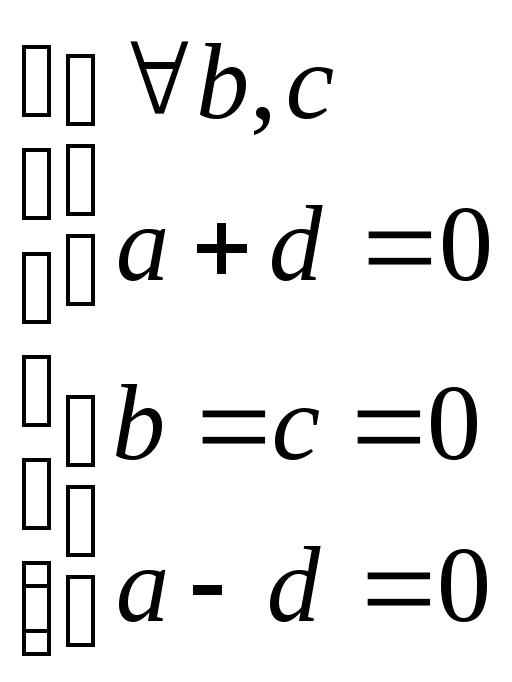
возможны два решения:

М= или М== а∙Е, а это не удовлетворяет определению инволюции.

Итак, матрица инволюции прямой М= Δ М= -(а² + bс) ≠ 0 (почему?)

Теорема. Пусть на проективной прямой даны пары точек А, А′ и В, В′, причем хотя бы в одной паре точки различны, тогда существует единственная инволюция переставляющая эти точки.

Т.е. А ↔ А′ и В ↔ В′ .

Доказательство. Пусть А ≠ А′ .

Рассмотрим проективное преобразование φ: А → А′ , А′ → А, В → В′ ,

по теореме о задании проективного преобразования прямой - это преобразование единственное, а в силу предыдущей теоремы это инволюция (А↔А′). □

Вывод: В инволюции всегда есть пара точек А ↔ А′.

Рассмотрим инволюцию и пару А ↔ А′. Если взять эти точки в качестве базисных точек репера, т.е. А и А′, тогда λ₁ А′ = ∙А=∙== а = 0, с = λ₁ ≠ 0.

λ₂ А= ∙А′=∙== b = λ₂ ≠ 0, а = 0.

М=, т.е. формулы проективного преобразования .

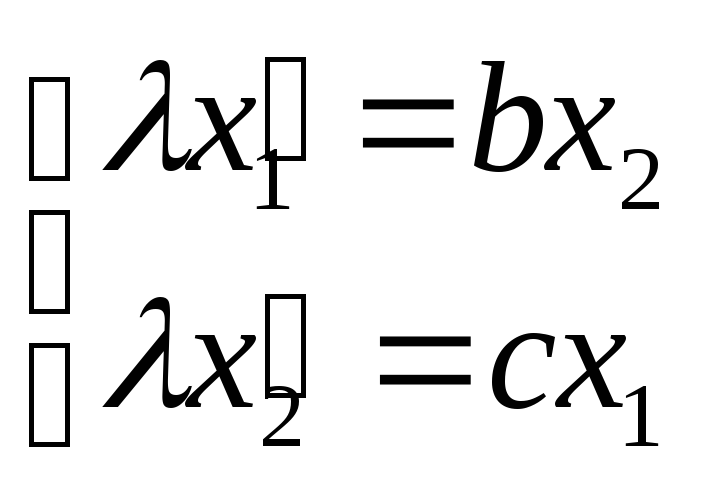Определение: Точка называется инвариантной точкой проективного преобразования, если при отображении она переходит сама в себя → λ∙Х=М∙Х.

Нахождение инвариантных точек сводится к нахождению собственных векторов и собственных значений матрицы.

det | М – λ ∙Е | = 0 – характеристическое уравнение.

= 0 λ ² – а ² – bс = 0 λ²=а²+ bс= -ΔМ.

1 случай: ΔМ < 0 - существует два решения λ_{1 , 2} = существуют две неподвижные точки.

2 случай: ΔМ > 0 - нет решения – нет неподвижных точек.

3 случай: ΔМ = 0 - не может быть (почему?).

Определение: Если существует две инвариантные точки, то инволюция называется гиперболической. Если не существует инвариантных точек, то инволюция называется - эллиптической.

Инвариантные точки:

При λ₁ = , ∙=

Х₁ = .

При λ ₂ = -, ∙=

Х₂ = .

Вывод: Инволюция может иметь или две неподвижные точки, или ни одной.

Свойства:

1. Для гиперболической инволюции любые две пары соответствующих точек не разделяют друг друга.

2. Для эллиптической инволюции любые две пары соответствующих точек разделяют друг друга.

Доказательство. Пусть в инволюции А ↔ А′ и В ↔ В′ .

Возьмем А и А′ за базисные точки репера М=.

Пусть В, причем b₁ ≠ 0 и b₂ ≠ 0 (почему?),

тогда λ∙В′=∙=

(АА′,ВВ′)=.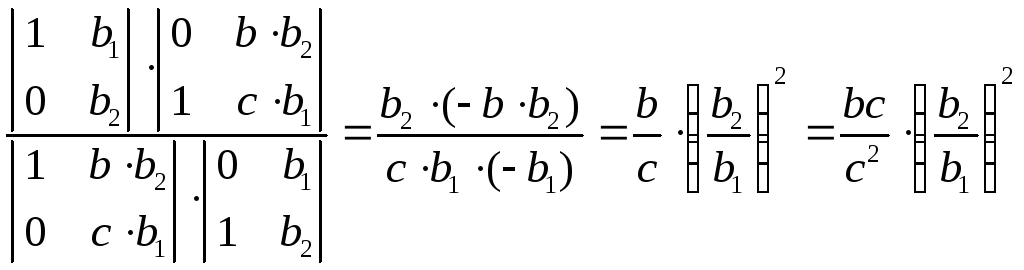

Таким образом:

Для гиперболической инволюции - det М = - b∙с < 0,

(АА′,ВВ′) > 0, т.е. пары не разделяют друг друга.

Для эллиптической инволюции - det М= - b∙с > 0,

(АА′,ВВ′) < 0, т.е. пары разделяют друг друга. □

3. Для эллиптической инволюции и любой пары соответствующих точек найдется единственная пара делящая первую гармонически.

Доказательство. Пусть А ↔ А′ . Доказать, что существует пара точек В↔В' такая, что (АА',ВВ')= -1.

Возьмем А и А′ за базисные точки репера.

Тогда М =.

Пусть В, причем х₁ ≠ 0 и х₂ ≠ 0, тогда В′=.

(АА′,ВВ′)== -1 (почему радикал существует?).

существует пара точек с координатами и .

Самостоятельно убедитесь, что В ↔ В′. □

4. Неподвижные точки гиперболической инволюции гармонически делят любую пару соответствующих точек А ↔ А′ .

Доказательство. Пусть А↔А′ , М₁ и М₂ - неподвижные точки.

(АА′, М₁М₂)=(А′А, М₁М₂)= (АА′,М₁М₂)² = 1

(АА′,М₁М₂) = ± 1. Если (АА′,М₁М₂)= 1 М₁ = М₂ , но неподвижные точки гиперболической инволюции различны, а значит (АА′,М₁М₂)= - 1. □

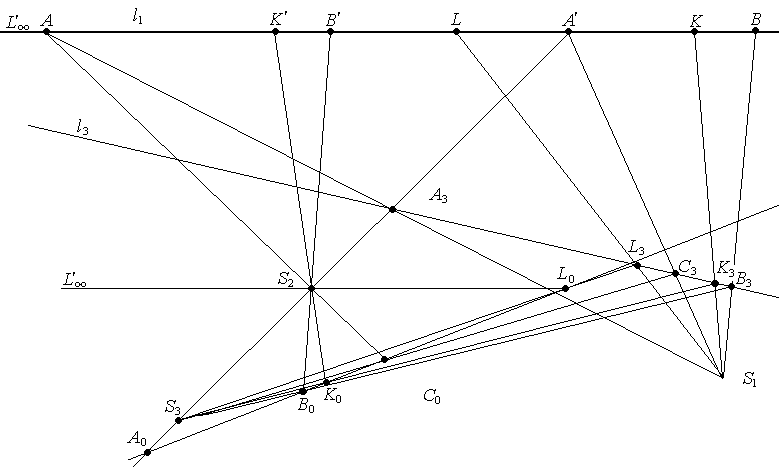
Построение образов и прообразов точек при инволюции прямой.

Задача. Инволюция задана точками А ↔ А′ и В ↔ В′. Построить образ и прообраз произвольных точек.

Решение. Решение соответствует второму случаю (ℓ₁ = ℓ₂) отображения φ: А → А′,В → В′, А′ → А.

Построение:

1. S₁ℓ₁ ,

2. ℓ₃ , такую, что S₁ ℓ₃ и ℓ₁ ≠ ℓ₃ ,

3. А₃ = ℓ₃ ∩ (S₁ А), В₃ = ℓ₃ ∩ (S₁В), С₃ = ℓ₃ ∩ (S₁ А′),

4. S₂ ≠ S₃ (А′А₃),

5. С₀ =(S₃С₃)∩(S₂А), В₀ =(S₃В₃)∩(S₂В′), А₀ =(В₀С₀)∩(А′А₃).

6. К К₃ =ℓ₃∩(S₃ К), К₀=(S₃К₃)∩(В₀С₀), К′=(S₂К₀)∩ℓ₁ .

7. L_∞ℓ₁, L₀=(S₂L₃)∩(В₀С₀), L₃=(S₃L₀)∩ℓ₃, L=(S₁L₃)∩ℓ₁.

8. Построение прообразов в обратном порядке (самостоятельно).

Задача. Дана гиперболическая инволюция и даны инвариантные точки М₁ и М₂ . Построить образ и прообраз произвольной точки А.

Решение. По свойству (4) → (АА′, М₁М₂)= - 1. Т.о. задача сводится к построению четвертой гармонической точки. Аналогично строится прообраз точки.

Задача. Даны точки А ↔ А′ и В ↔ В′. Найти уравнение инволюции.

Решение. Пусть матрица инволюции М=, тогда формулы λ∙Х ′ = М∙Х и λ∙Х = М∙Х ′.

Подставим точки:

λ₁∙А′= М∙А ,

λ₂∙А= М∙А′ ,

λ₃∙В′= М∙В ,

λ₄∙В= М∙В′ .

.

Одно из решений а = 7, b= - 5, с= 2, М=.

Уравнение инволюции: λ∙Х ′ = ∙Х.

Задача. Известны неподвижные точки инволюции - М₁ и М₂ , найти её уравнение.

Решение. Пусть матрица инволюции М=,

тогда формулы преобразования λ∙Х′= М∙Х и λ∙Х= М∙Х′, для инвариантных точек λ∙Х= М∙Х .

Подставим наши точки: λ₁∙М₁= М∙М₁, λ₂∙М₂= М∙М₂ .

.

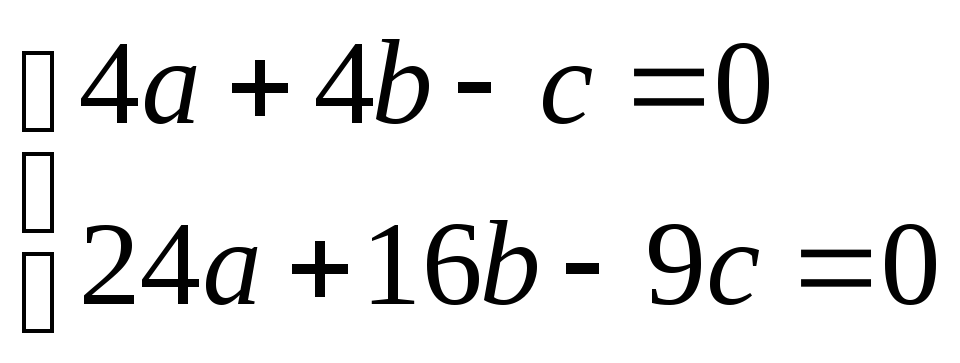Одно из решений а = -5, b= 3, с= - 8, М=.

Уравнение инволюции: λ∙Х ′ = ∙Х .

Задача. Найти неподвижные точки инволюции .

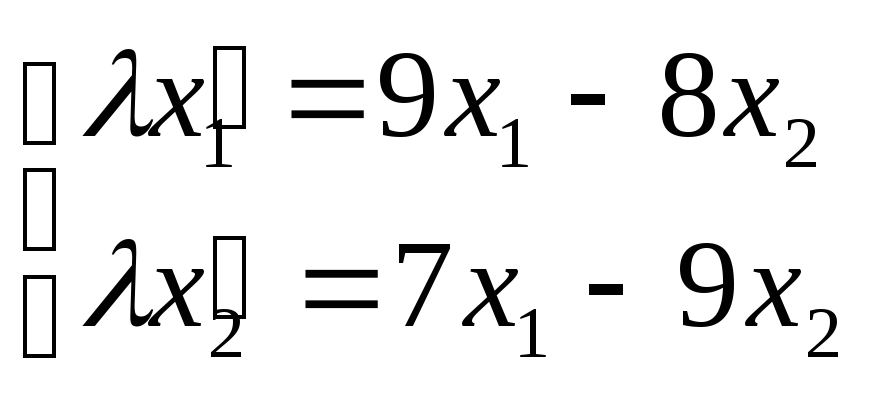Решение. Матрица инволюции М=.

Тогда характеристическое уравнение λ ² - 9² –(-8)∙7 = 0 λ ²= 25 λ = ± 5.

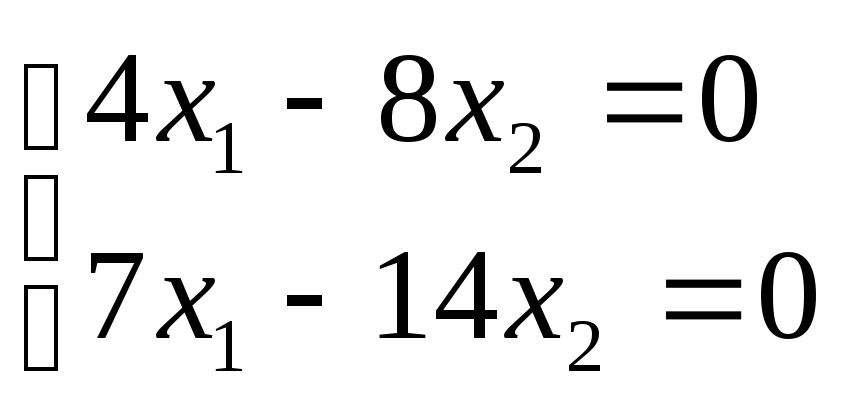
При λ₁ = 5, ∙= х₁ = 2∙х₂ , М₁ = .

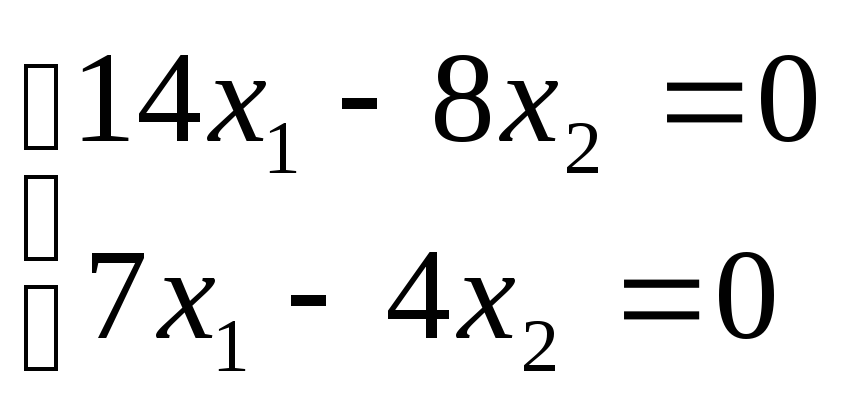
При λ ₂ = -5 , ∙= 7∙х₁ = 4∙х₂ , М₂ = .