Квадрики на проективной плоскости

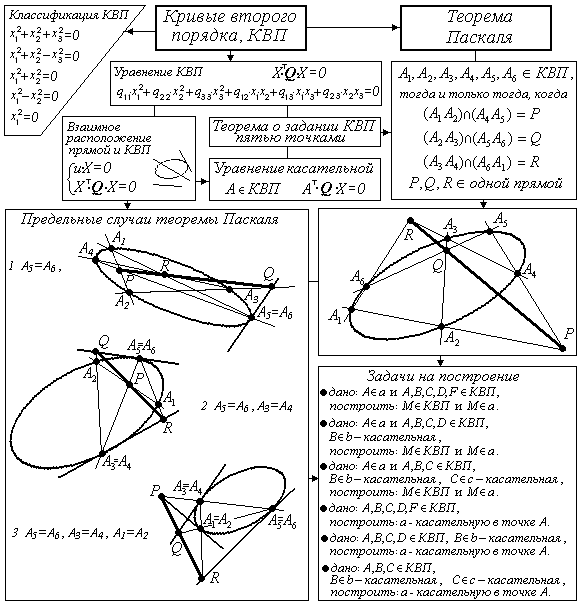
Рассмотрим проективную плоскость над полем действительных чисел (т.е. координаты точек могут быть только действительными числами).

Определение: Множество точек на проективной плоскости Р₂ координаты которых в некотором репере удовлетворяют уравнению q _i j ∙х _i ∙х _j = 0 - называется квадрикой или кривой второго порядка (КВП).

В развернутом виде получим: q₁₁∙х₁²+ q₂₂∙х₂² + q₃₃∙х₃²+ 2∙q₁₂∙х₁∙х₂ + 2∙q₁₃∙х₁∙х₃ + 2∙q₂₃∙х₂∙х₃ =0 (*)

Замечание: В силу того, что уравнение квадрики – это однородное уравнение второго порядка, коэффициенты уравнения определяются с точностью до пропорциональности. Т.е. квадрика определена набором из шести чисел с точностью до пропорциональности и среди этих наборов нет нулевого набора ( 0 : 0 : 0 : 0 : 0 : 0 ). (Почему?)

Определение: Матрица Q=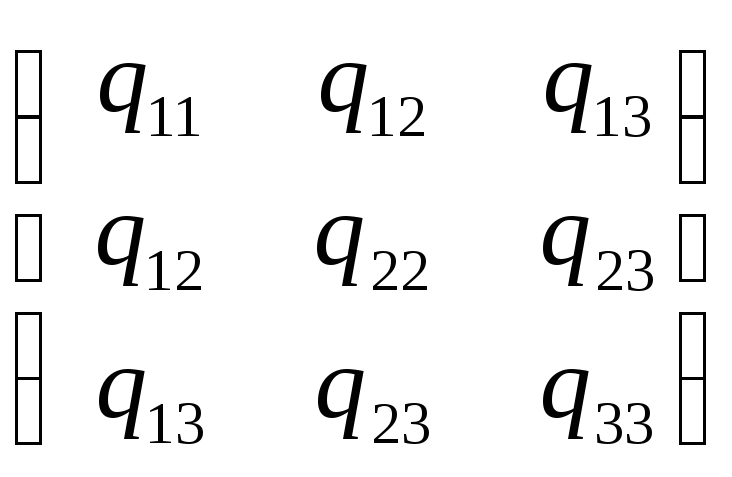 - называется матрицей квадрики.

Замечание: Матрица Q является симметричной, Q=Q^Т .

Уравнение (*) в матричном виде примет вид:

∙∙=0 или Х ^Т∙Q∙Х =0 (проверьте).

Свойства квадрик:

1. Ранг матрицы квадрики инвариантен относительно линейного преобразования, задаваемого матрицей А: rangQ = rang(A^T∙Q∙A), так как det A≠0.

2. Преобразованием координат можно привести квадрику к каноническому виду - λ₁∙x₁² + λ₂∙x₂² + λ₃∙x₃² =0, где λ_i - собственные значения матрицы Q.

Замечание: Эти свойства квадрик вытекают из свойств квадратичных форм.

Делая проективное преобразование 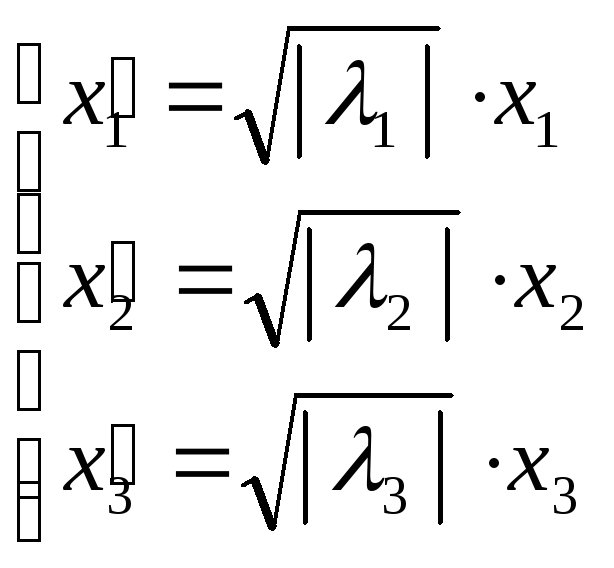, квадрику можно привести к виду:

ε₁∙x₁² + ε₂∙x₂² + ε₃∙x₃² =0, где ε_i = - 1, 0, 1.

Т.е матрица примет вид - 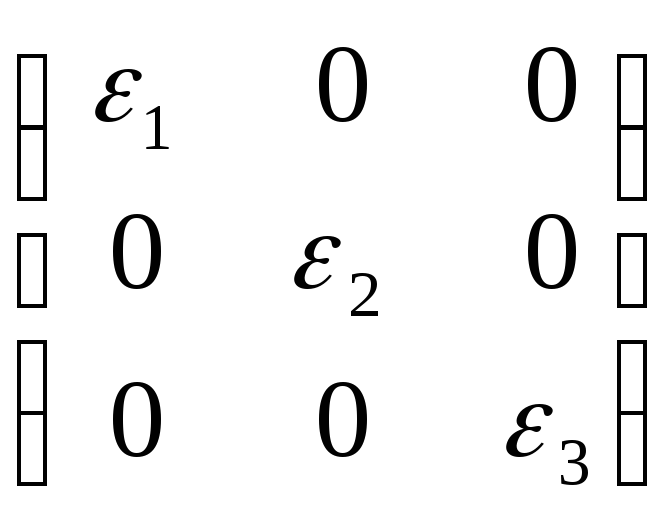и её ранг равен числу ненулевых ε_i.

Классификация кривых второго порядка на проективной плоскости.

Пусть квадрика приведена к каноническому виду.

Для ε_i = - 1, 0, 1 всего различных комбинаций будет - 3³=27.

1. ε₁ =1, ε₂ = 1, ε₃ = 1 rangQ= 3.

x₁² + x₂² + x₃² = 0 - этому уравнению удовлетворяет только точка , но на проективной плоскости Р₂ нет такой точки. (Почему?)

Т.е. ни одна точка Р₂ не удовлетворяет этому уравнению. Такую квадрику будем называть нулевой.

Замечание: Нулевой квадрикой также будет - x₁² - x₂² - x₃² = 0.

2. ε₁ =1, ε₂ = 1, ε₃ = - 1 rangQ= 3.

x₁² + x₂² - x₃² = 0 - этому уравнению удовлетворяет множество точек. Такую квадрику будем называть овальной.

Замечание: Овальными также будут: x₁² - x₂² + x₃² = 0, - x₁² + x₂² + x₃² = 0,

- x₁² - x₂² + x₃² = 0, - x₁² + x₂² - x₃² = 0, x₁² - x₂² - x₃² = 0.

3. ε₁ =1, ε₂ = 1, ε₃ = 0 rangQ= 2.

x₁² + x₂² = 0 - этому уравнению удовлетворяет только одна точка с действительными координатами Е₃ и множество точек с мнимыми координатами. Эта квадрика является пересечением двух мнимых прямых x₁ = ± i∙x₂ , которые пересекаются одной действительной точке Е₃ .

Замечание: К этому же классу относятся квадрики: x₁² + x₃² = 0, x₂² + x₃² = 0,

- x₁² - x₂² = 0, - x₁² - x₃² = 0, - x₂² - x₃² = 0.

4. ε₁ =1, ε₂ = - 1, ε₃ = 0 rangQ= 2.

x₁² - x₂² = 0 - этому уравнению удовлетворяет множество точек с действительными координатами.

Так как x₁² - x₂² = ( x₁ - x₂)·( x₁ + x₂),

то эта квадрика является пересечением двух прямых x₁ = x₂ и x₁ = - x₂.

Замечание: К этому же классу относятся квадрики: x₁² - x₃² = 0, x₂² - x₃² = 0,

- x₁² + x₂² = 0, - x₁² + x₃² = 0, - x₂² + x₃² = 0.

5. ε₁ =1, ε₂ = 0, ε₃ = 0 rangQ= 1.

x₁² = 0 - этому уравнению удовлетворяет множество точек с действительными координатами. Эта квадрика является парой совпавших прямых x₁ =0 и x₁=0.

Замечание: К этому же классу относятся квадрики: х₂² = 0, x₃² = 0,

- x₁²= 0, - x₂² = 0, - x₃² = 0.

6. ε₁ =0, ε₂ = 0, ε₃ = 0 rangQ= 0.

0∙x₁² + 0∙x₂² + 0∙x₃² =0- этому уравнению удовлетворяют все точки проективной плоскости. Поэтому как квадрику это уравнение не рассматривают.

Вывод: На проективной плоскости существует пять классов квадрик

№	Класс		rangQ	Уравнение
1	Мнимая	невырожденная	rangQ= 3	x1²+x2²+x3²=0
2	Овальная	невырожденная	rangQ= 3	x1²+x2²-x3²=0
3	Пара мнимых пересекающихся прямых	вырожденная	rangQ= 2	x1² + x2² = 0
4	Пара действительных пересекающихся прямых	вырожденная	rangQ= 2	x1² - x2² = 0
5	Пара совпавших прямых	вырожденная	rangQ= 1	x1² = 0

Теорема. Каковы бы ни были пять точек на проективной плоскости среди которых никакие четыре не лежат на одной прямой, существует единственная квадрика инцидентная им.

Доказательство. Пусть точки будут А, В, С, D, H. Из данных пяти точек коллинеарными может быть только три. Если никакие три точки не лежат на одной прямой, то любые четыре можно выбрать в качестве репера плоскости. Если есть три точи лежащие на одной прямой, например А, В, С, то оставшиеся D и H не лежат на этой прямой. Тогда в качестве точек репера возьмем А, В, D, H.

R(А, В, D, H), тогда А , В , D , H , С .

Подставим координаты точек в уравнение (*), получим:

А q₁₁∙1² + q₂₂∙0² + q₃₃∙0² + 2q₁₂∙1∙0 + 2q₁₃∙1∙0 + 2q₂₃∙0∙0 = 0,

В q₁₁∙0² + q₂₂∙1² + q₃₃∙0² + 2q₁₂∙0∙1 + 2q₁₃∙0∙0 + 2q₂₃∙1∙0 = 0,

D q₁₁∙0² + q₂₂∙0² + q₃₃∙1² + 2q₁₂∙0∙0 + 2q₁₃∙0∙1 + 2q₂₃∙0∙1 = 0,

Н q₁₁∙1² + q₂₂∙1² + q₃₃∙1² + 2q₁₂∙1∙1 + 2q₁₃∙1∙1 + 2q₂₃∙1∙1 = 0,

С q₁₁∙с₁ ² + q₂₂∙с₂² + q₃₃∙с₃² + 2q₁₂∙с₁∙с₂ + 2q₁₃∙с₁∙с₃ + 2q₂₃∙с₂∙с₃=0,

q₁₁ = 0, q₂₂ = 0, q₃₃ = 0, q₁₂ + q₁₃ + q₂₃ = 0, q₁₂∙с₁∙с₂ + q₁₃∙с₁∙с₃ + q₂₃∙с₂∙с₃ = 0.

Матрица системы имеет ранг 2, в противном случае точка С совпадала бы с одной из точек репера (проверьте). Значит, существуют ненулевые решения, т.е. квадрика существует. Найдем их.

→ q₁₂= с₂∙с₃ - с₁∙с₃ , q₁₃= с₁∙с₂ - с₂∙с₃ , q₂₃=с₁∙с₃ -с₁∙с₂.

Или q₁₂ = с₃∙(с₂ - с₁), q₁₃ = с₂∙(с₁ - с₃), q₂₃=с₁∙(с₃ - с₂)

с₃∙(с₂ - с₁)∙х₁∙х₂ + с₂∙(с₁ - с₃)∙х₁∙х₃ + с₁∙(с₃ - с₂)∙х₂∙х ₃ = 0 - уравнение квадрики в репере R(А, В, D, H). □

Замечание: Если среди пяти точек никакие три не коллинеарны, то через них нельзя провести двух прямых, а значит, квадрика будет овальной. Если есть тройка коллинеарных точек, через две оставшиеся можно провести вторую прямую и квадрика распадается на две прямые.

Задача. Составить уравнение квадрики проходящей через точки

А , В , D , H , С .

Решение. Подставим координаты точек в уравнение (*).

А q₁₁∙2² + q₂₂∙1² + q₃₃∙0² + 2q₁₂∙2∙1 + 2q₁₃∙2∙0 + 2q₂₃∙1∙0 = 0,

В q₁₁∙2²+ q₂₂∙(-1)² + q₃₃∙0² + 2q₁₂∙2∙(-1) + 2q₁₃∙2∙0 + q₂₃∙(-1)∙0=0,

D q₁₁∙0² + q₂₂∙0² + q₃₃∙1² + 2q₁₂∙0∙0 + 2q₁₃∙0∙1 + 2q₂₃∙0∙1 = 0,

Н q₁₁∙(-2)²+ q₂₂∙0² + q₃₃∙1² + 2q₁₂∙(-2)∙0 + 2q₁₃∙(-2)∙1 +2q₂₃∙0∙1=0,

С q₁₁∙2 ² + q₂₂∙ 2² + q₃₃∙ 3² + 2q₁₂∙ 2∙ 2 + 2q₁₃∙ 2∙ 3 +2q₂₃∙ 2∙ 3 = 0,

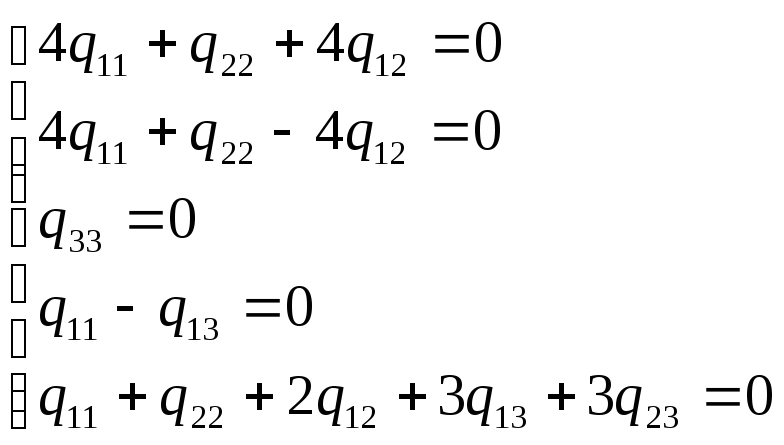
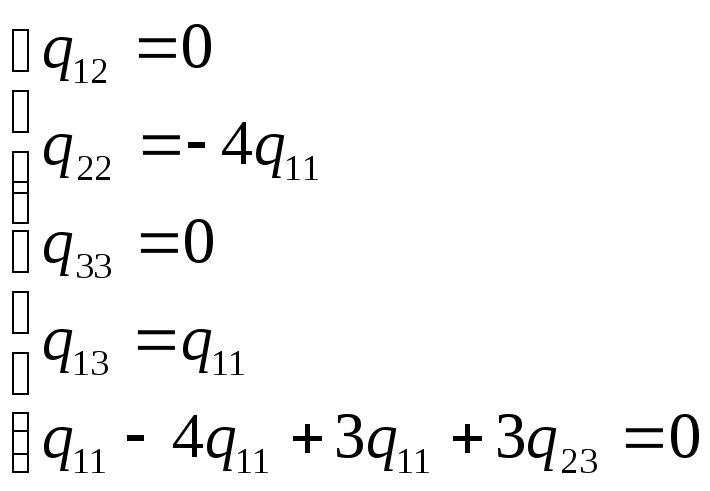
q₁₁∙х₁² - 4∙q₁₁ ∙х₂² + 2∙q₁₁ ∙х₁∙х₃ =0 х₁² - 4∙х₂² + 2∙х₁∙х₃ = 0

(разделили на q₁₁ ≠ 0, так как все коэффициенты одновременно не могут быть равными 0).

Задача. Привести уравнение квадрики 2∙х₂² - 3∙х₃² - 2∙х₁∙х₂ - 2∙х₁∙х₃ - 2∙х₂∙х₃ =0 к каноническому виду.

Решение. Один из способов приведения КВП к каноническому виду основан на применении собственных векторов и собственных значений матрицы. Но этот способ довольно громоздкий.

Приведем КВП к каноническому виду методом Лагранжа (метод выделения полных квадратов).

(∙х₂)² - 2∙х₁∙х₂ + 2∙х₁∙х₃ - 2∙х₂∙х₃ +х₁² +

+х₃² -2∙х₁∙х₃ - х₁² -х₃² - 3∙х₃² - 2∙х₁∙х₃ =

=(х₁ +х₃ - ∙х₂)² - 3∙х₁∙х₃ - х₃² - х₁² = (х₁ +х₃ - ∙х₂)² - (3∙х₁∙х₃ +7 х₃² + х₁²)=

=(х₁ +х₃ - ∙х₂)² - (х₁² + 2∙х₁∙х₃ +х₃² - х₃² +7х₃²)=

=(х₁ +х₃ - ∙х₂)² - (х₁ +х₃ )² + х₃² -7х₃²=(х₁ +х₃ - ∙х₂)² - (х₁ +х₃ )² - х₃² =(х₁ +х₃ - ∙х₂)² - (х₁ +х₃ )² - (х₃) ² =0,

(х₁ +х₃ )² + (х₃) ² - (х₁ +х₃ - ∙х₂)² = 0.

Если ввести новые переменные 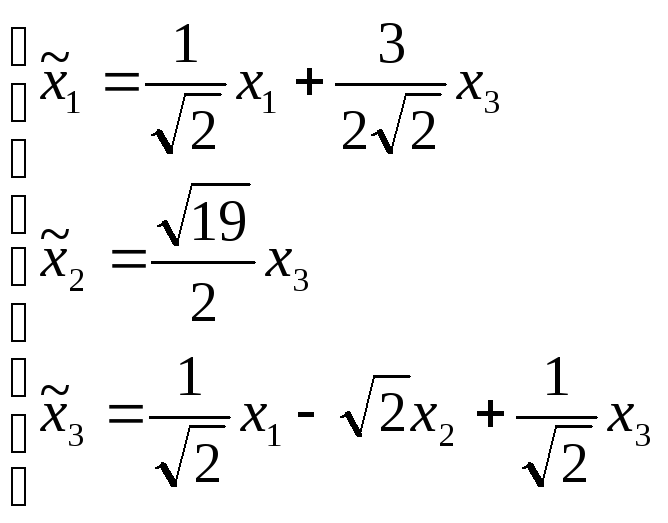, тогда в

новых координатах уравнение квадрики примет вид: - это овальная квадрика.

Выделить полные квадраты можно и другим способом:

2∙х₂² - 3∙х₃² - 2∙х₁∙х₂ - 2∙х₁∙х₃ - 2∙х₂∙х₃ =0 | : 2

х₂² - 1,5∙х₃² - х₁∙х₂ - х₁∙х₃ - х₂∙х₃ =

= х₂² - 2∙х₂∙0,5·х₁ - 2∙х₂∙0,5·х₃ + 2∙0,5·х₁∙0,5·х₃ + 0,25∙х₁² +0,25∙х₃² -

- 0,25∙х₁² - 0,25∙х₃² - 0,5∙х₁∙х₃ - х₁∙х₃ - 1,5∙х₃² =

= (х₂ - 0,5·х₁ - 0,5·х₃)² - 0,25∙х₁² - 1,5∙х₁∙х₃ - 1,75∙х₃² = (х₂ - 0,5·х₁ - 0,5·х₃)² - 0,25∙(х₁² + 6∙х₁∙х₃ + 7∙х₃²)=

= (х₂ - 0,5·х₁ - 0,5·х₃)² - 0,25∙(х₁² + 2∙х₁∙3∙х₃ + 9∙х₃² - 2∙х₃²)=

= (х₂ - 0,5·х₁ - 0,5·х₃)² - 0,25∙(х₁ + 3∙х₃)² + 0,5∙х₃² = 0 | × 4

4∙(х₂ - 0,5·х₁ - 0,5·х₃)² - (х₁ + 3∙х₃)² + 2∙х₃² = 0 (2·х₂ - х₁ - х₃)² - (х₁ + 3∙х₃)² + 2∙х₃² = 0.

Введя новые переменные 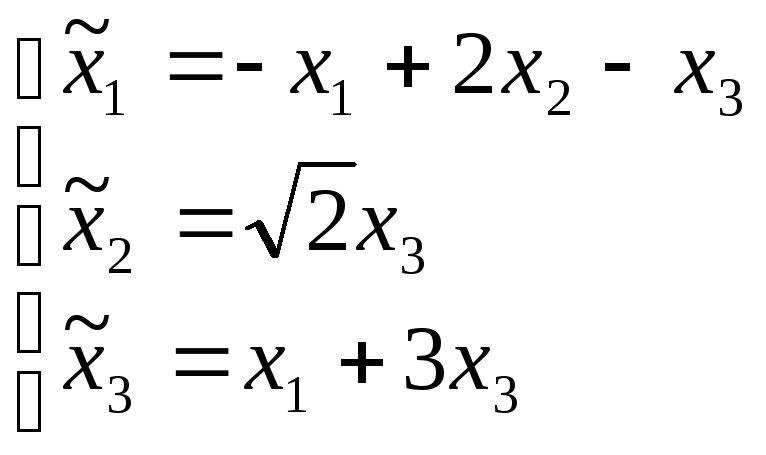, уравнение квадрики примет вид: - это овальная квадрика.