Координаты точки на прямой (плоскости)

Рассмотрим P₁ и R(Е₁ , Е₂ , Е) - проективный репер на прямой

Пусть ē₁ , ē₂ , ē - согласованная система векторов и пусть точка МP₁ порождается вектором .

Векторы ē₁ , ē₂ – базисные, тогда =х₁∙ē₁+х₂∙ē₂.

Определение: Набор чисел ( х₁ , х₂ ) называется координатами точки в данном репере.

Вектор = λ∙=λ∙х₁∙ē₁+λ∙х₂∙ē₂ - определяет ту же точку М.

Тогда, точка М определяется набором или (х₁ , х₂) или (λ∙х₁ , λ∙х₂).

Вывод: Координаты точки определены с точностью до постоянного множителя (до пропорциональности).

Обозначение: М ( х₁ : х₂ ) или .

На проективной плоскости координаты определяются аналогично:

Обозначение: М ( х₁ : х₂ : х₃ ) или .

Замечание: Числа х₁ и х₂ (для плоскости - х₁ , х₂ , х₃ ) одновременно не обращаются в ноль(Почему?).

Координаты точек репера на прямой будут:

вершины - Е₁, Е₂, единичная точка - Е,

на плоскости - Е₁( 1 : 0 : 0 ), Е₂( 0 : 1 : 0 ), Е₃( 0 : 0 : 1 ), Е( 1 : 1 : 1 ) (Обоснуйте).

Построение точек по координатам на прямой

Рассмотрим построение точек по координатам на примере.

Задача. Дана модель «пучок прямых» и R(Е₁ , Е₂ , Е).

Построить точки

А , В , С , К , М.

Решение. С учетом пропорциональности координат точек будут:

А , В , С=Е₁ , К =Е, М.

Началом системы координат будем считать точку S – центр пучка.

На прямых (SЕ), (SЕ₁), (SЕ₂) выберем векторы ē , ē₁ , ē₂ так, чтобы ē = ē₁+ ē₂.

В базисе ē₁ , ē₂ построим векторы ā =( 1 ; 4 ), =( -2 ; 15 ), =( 1 ; - 1 ).

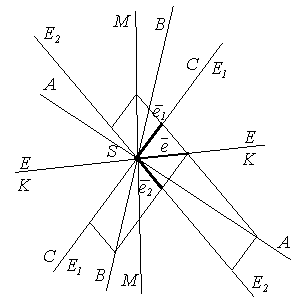
Прямые пучка содержащие векторы ā , , - будут проективными точками.

Задача. Дана расширенная евклидова прямая и R(Е₁ , Е₂ , Е).

Построить точки

А , В , С , К , М.

Решение. С учетом пропорциональности координат точек будут:

А, В, С=Е₁ , К =Е , М.

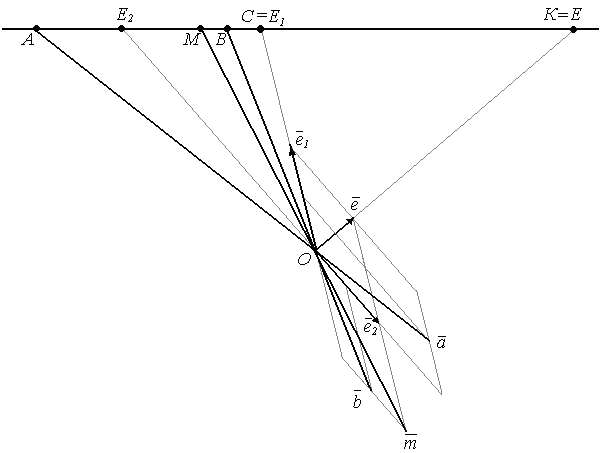
Возьмем произвольную точку О не лежащую на прямой, проведем прямые (ОЕ), (ОЕ₁), (ОЕ₂).

На этих прямых выберем векторы ē , ē₁ , ē₂ так, чтобы ē=ē₁+ē₂.

В базисе ē₁ , ē₂ построим векторы

ā =( 0,5 ; 2 ), =( -1 ; 0,5 ), =( -1 ; 1 ).

Принадлежность трёх точек одной прямой

Пусть А, В, С - различные точки на P₂, тогда векторы, порождающие эти точки:

ā =( а₁ : а₂ : а₃), = ( b₁ : b₂ : b₃ ), = ( с₁ : с₂ : с₃ ).

Точки могут лежать на одной прямой или не лежать на одной прямой.

1. А, В, С P₁, тогда ā, , L₂ ā, , - линейно-зависимы

такие, что = α∙ā + β∙

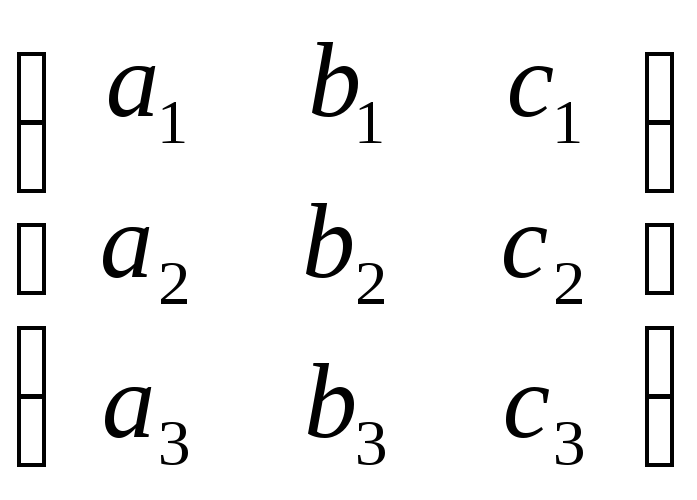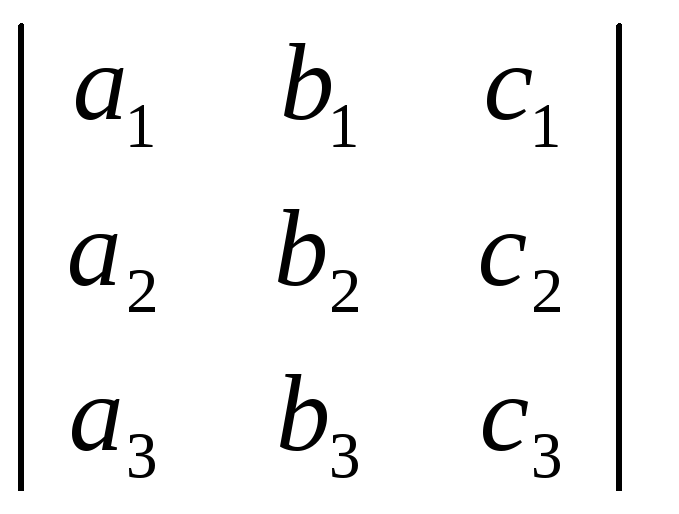=α∙+β∙, или rg= 2, или = 0.

Определение: Точки лежащие на одной прямой называются коллинеарными.

2. Пусть А, В P₁ и С P₁ , тогда векторы ā, , L₂

ā, , - линейно-независимы ≠ α∙ā + β∙

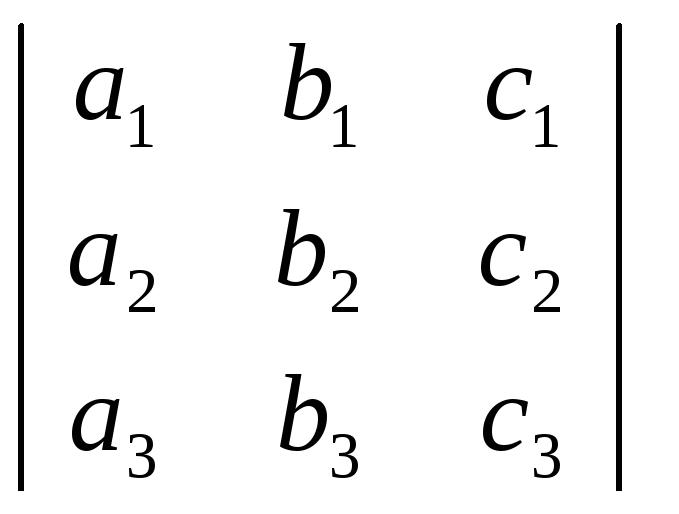≠ α∙+ β∙, или rg≠ 2, или ≠ 0.

Вывод: Для того, чтобы точки А, В, С были коллинеарными необходимо и достаточно выполнение одного из условий:

α, β такие, что =α∙+ β∙ или С= α∙А+ β∙В;

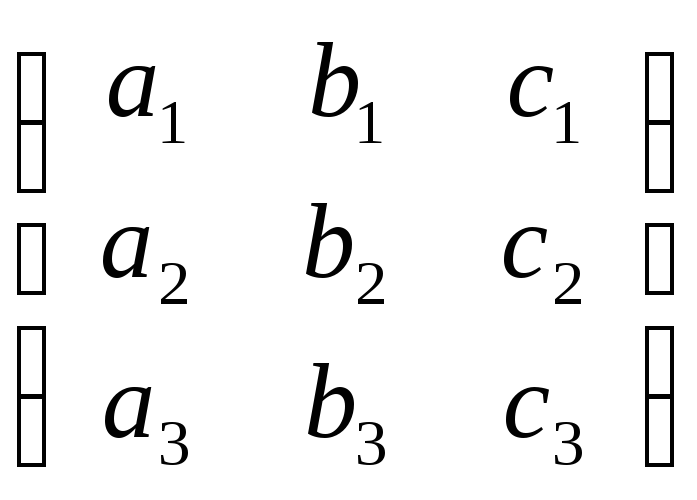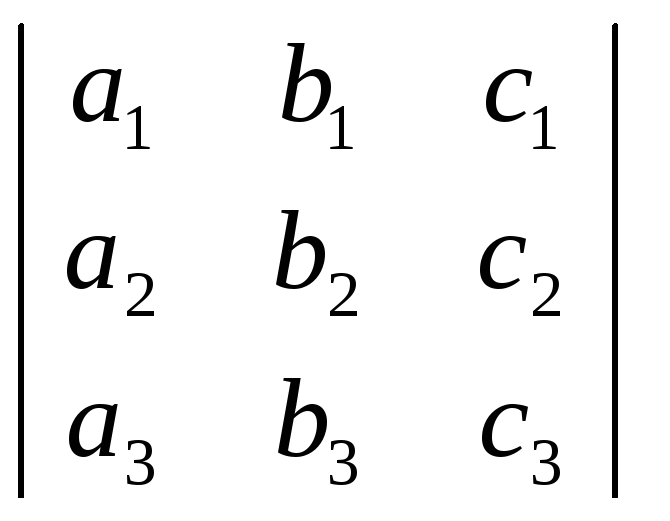rg= 2 или = 0.

Замечание: Для проверки коллинеарности большего количества точек удобнее проверять условие rg М = 2, где М – матрица, составленная из координат точек. (Обоснуйте!).

Рассмотрим условие принадлежности какой-либо точки одной из координатных прямых: (Е₁Е₂), (Е₁Е₃), (Е₂Е₃).

Пусть М (Е₁Е₂), тогда 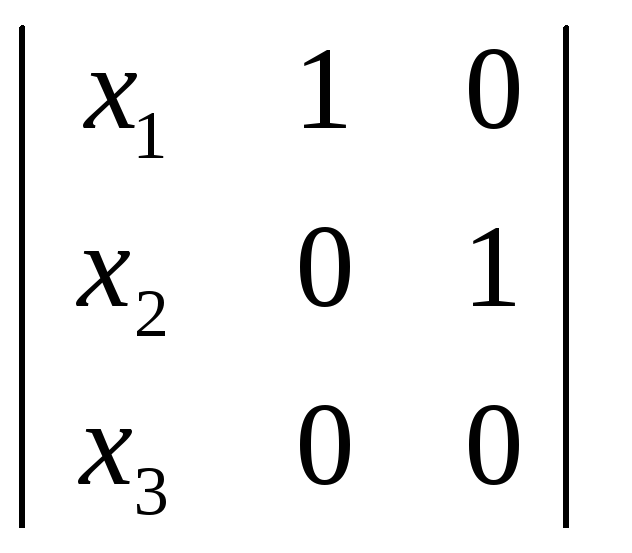=0 х₃ = 0.

Аналогично: М (Е₁Е₃), тогда х₂ = 0; М (Е₂Е₃), тогда х₁ = 0.

Вывод: Если одна из координат точки равна 0, тогда точка принадлежит одной из координатных прямых.

Могут ли три координаты точки равняться 0? А две?

Пусть точка Х отлична от вершин репера.

Определение: Проекцией точки Х из Е₃ на (Е₁Е₂) называется точка Х₃ такая, что Х₃= (ХЕ₃)∩(Е₁Е₂).

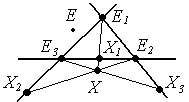
Аналогично определяются проекции из Е₂ и Е₁:

Х₁= (ХЕ₁)∩(Е₂Е₃),

Х₂=(ХЕ₂)∩(Е₁Е₃).

Тогда Х= (Х₁Е₁) ∩ (Х₁Е₂) ∩ (Х₃Е₃).

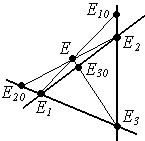
Пусть Е₁₀ , Е₂₀ , Е₃₀. - проекции точки Е на координатные прямые,

тогда на каждой прямой возникает свой репер:

на (Е₁Е₂) - R(Е₁ , Е₂ , Е₃₀),

на (Е₁Е₃) - R(Е₁ , Е₃ , Е₂₀),

на (Е₂Е₃) - R(Е₂ , Е₃ , Е₁₀).

Теорема о проекциях. Пусть R(Е₁ , Е₂ , Е₃ , Е) - репер на проективной плоскости, точка Х отлична от точек репера, точки Х₁ , Х₂ , Х₃ – проекции точки Х на соответствующие координатные прямые. Тогда

точка Х₁ в R(Е₂ , Е₃ , Е₁₀) будет иметь координаты ( х₂ : х₃),

точка Х₂ в R(Е₁ , Е₃ , Е₂₀) будет иметь координаты - ( х₁ : х₃),

точка Х₃ в R(Е₁ , Е₂ , Е₃₀) будет иметь координаты - ( х₁ : х₂).

Доказательство. Докажем для одной проекции точки, для остальных доказательство по аналогии.

Пусть Х₁ , т.к. Х₁(Е₂Е₃), тогда у₁= 0 Х₁ .

Точки Х, Х₁ , Е₁ - принадлежат одной прямой

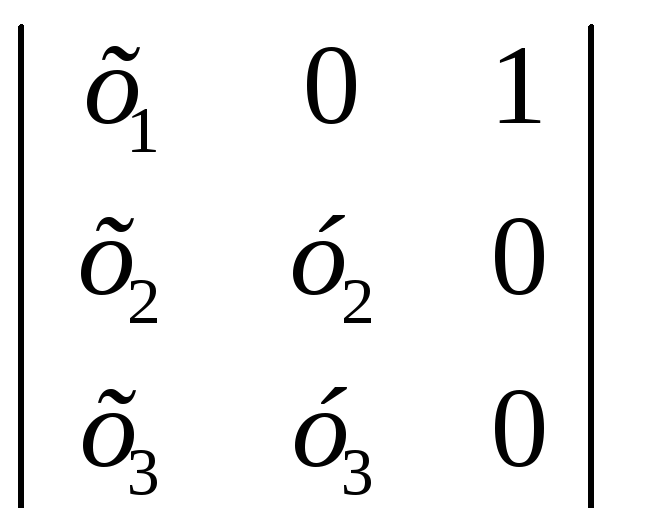=0 х₂∙у₃ – х₃∙у₂=0 у₂= λ ∙х₂ , у₃ = λ ∙х₃

Х₁ 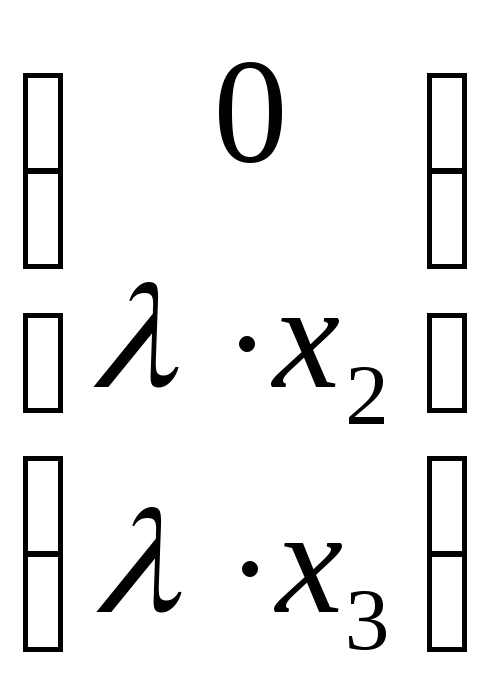или Х₁ , аналогично: Х₂ и Х₃ .

Тогда проекции точки Е на координатные прямые будут иметь координаты:

Е₁₀ , Е₂₀ , Е₃₀ т.к. Е .

Рассмотрим: Е₁₀ , Е₂, Е₃ и Х₁- они все лежат на прямой (Е₁Е₂).

Рассмотрим векторы, порождающие эти точки в базисе ē₁ , ē₂ , ē₃ :

ē₁₀ = 0 ∙ ē₁ + 1 ∙ ē₂ + 1 ∙ē₃ , → ē₁₀ = 1 ∙ ē₂ + 1 ∙ē₃ ,

ē₂ = 0 ∙ ē₁ + 1 ∙ ē₂ + 0 ∙ē₃ , → ē₂ = 1 ∙ ē₂ + 0 ∙ē₃ ,

ē₃ = 0 ∙ ē₁ + 0 ∙ ē₂ + 1 ∙ē₃ , → ē₃ = 0 ∙ ē₂ + 1 ∙ē₃ ,

= 0 ∙ ē₁ + х₂ ∙ ē₂ + х₃ ∙ē₃ , → = х₂ ∙ ē₂ + х₃ ∙ē₃ .

Но векторы ē₂ , ē₃ линейно-независимы, система ē₂, ē₃ , ē₁₀ - согласована (ē₂+ ē₃=ē₁₀), а значит точки Е₂ , Е₃ , Е₁₀ образуют репер R(Е₂ , Е₃ , Е₁₀ ) и точка Х₁ в нем имеет координаты ( х₂ : х₃). □

Замечание: Это теорема позволяет легко строить точки на проективной плоскости по их проекциям, т.к. Х= (Х₁Е₁)∩(Х₁Е₂)∩(Х₃Е₃).

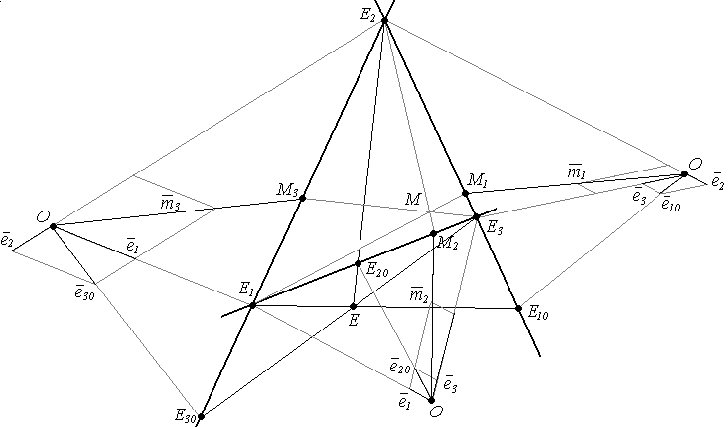
Построение точек по координатам на плоскости

Рассмотрим построение точек по координатам на примере.

Задача. На расширенной евклидовой плоскости построить точку М .

Решение. Пусть М₁ , М₂ , М₃ - проекции точки М на соответствующие координатные прямые.

Тогда проекция точки М - точка М₁ в R(Е₂ , Е₃ , Е₁₀) будет иметь координаты (-2 : 4 ) или ( -1 : 2 ),

точка М₂ в R(Е₁ , Е₃ , Е₂₀) будет иметь координаты (1 : 4),

точка М₃ в R(Е₁ , Е₂ , Е₃₀) будет иметь координаты ( 1 : -2 ).

При построении проекций будем пользоваться построением точек на проективной прямой.

Восстановим базисы на каждой координатной прямой.

Например, на прямой (Е₁Е₂) - R(Е₁ , Е₂ , Е₃₀).

Берем произвольную точку О, на прямой на (ОЕ₃₀), выбираем произвольный вектор ē₃₀ – раскладываем его по векторам ē₁ и ∙ē₂ , которые лежат на прямых (ОЕ₁) и (ОЕ₂).

В этом базисе построим вектор = - ē₂ - 2∙ē₃,.

Точка М₁ лежит на прямой (Е₁Е₂) – продляем прямую, содержащую вектор до пересечения с прямой (Е₁Е₂).

Аналогично на прямой (Е₁Е₃) в репере R(Е₁ , Е₃ , Е₂₀), строим вектор = ē₁ + 4∙ē₃ и точку М₂ .

На прямой (Е₂Е₃) в репере R(Е₁ , Е₂ , Е₃₀) - = ē₁ - 2∙ē₂ и точку М₃ .

Точка М = (Е₁М₁) ∩ (Е₂М₂) ∩ (Е₃М₃).