Прямые и квадрики на расширенной евклидовой плоскости

Рассмотрим расширенную евклидову плоскость Р₂ и однородный репер R(Е_1∞ , Е_2∞ , Е₃ , Е).

В этом случае связь между проективными и аффинными координатами будет выражаться формулами: х = и у = .

Для собственных точек плоскости координата х₃≠0, для несобственных - х₃=0.

Пусть дана прямая и : и₁ х₁+ и₂ х₂+ и₃ х₃ =0.

Прямая содержит только одну несобственную точку U_∞ (проверьте!)

Все остальные точки собственные, тогда мы можем разделить уравнение прямой на х₃ ≠ 0 ,

получим: и₁ + и₂ + и₃=0 и₁ х + и₂ у + и₃=0 – общее уравнение прямой на евклидовой плоскости с направляющим вектором ā ( и₂ ; - и₁ ) (сравнить с координатами несобственной точки).

Как известно, если две прямые параллельны, то их направляющие вектора коллинеарны:

ā ( и₂ ; - и₁ ) || ( λи₂ ; - λи₁ ). Тогда несобственная точка второй прямой будет иметь координаты:

== U_∞ - это означает, что параллельные в евклидовом смысле прямые пересекаются в несобственной точке. На евклидовой плоскости таких точек нет, а значит параллельные в евклидовом смысле прямые не пересекаются на евклидовой плоскости, но пересекаются на проективной плоскости.

Пусть дана квадрика: q₁₁∙х₁²+q₂₂∙х₂²+q₃₃∙х₃²+2∙q₁₂∙х₁∙х₂+2∙q₁₃∙х₁∙х₃+2∙q₂₃∙х₂∙х₃=0.

Разделим уравнение КВП на х₃² ≠ 0, получим:

q₁₁∙+q₂₂∙+q₃₃+2∙q₁₂∙∙+2∙q₁₃∙+2∙q₂₃∙=0

q₁₁∙х² + 2∙q₁₂∙х∙у + q₂₂∙у² + 2∙q₁₃∙х + 2∙q₂₃∙у + q₃₃ =0 – общее уравнение КВП на евклидовой плоскости.

Как известно тип КВП на евклидовой плоскости определяется инвариантом

J₂ = = q₁₁∙q₂₂ - q₁₂².

J₂>0 – эллиптический, J₂<0 – гиперболический, J₂=0 – параболический типы.

Найдем несобственные точки квадрики.

Это точки для которых х₃ = 0.

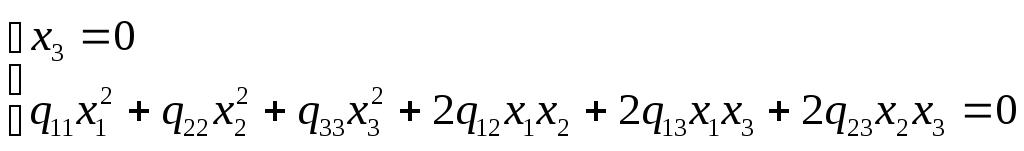
Так все три координаты х₁ , х₂ , х₃ одновременно не обращаются в 0, то хотя бы одна х₁ или х₂ не равны 0. Пусть это будет х₂ ≠ 0. Разделим второе уравнение системы на х₂ ≠ 0:

q₁₁∙+2∙q₁₂∙ + q₂₂ =0 – квадратное уравнение. D= q₁₂². - q₁₁∙q₂₂ = - (q₁₁∙q₂₂ - q₁₂²) = - J₂

Таким образом, у линии эллиптического типа нет несобственных точек, у линии параболического типа одна несобственная точка –

, у линии гиперболического типа 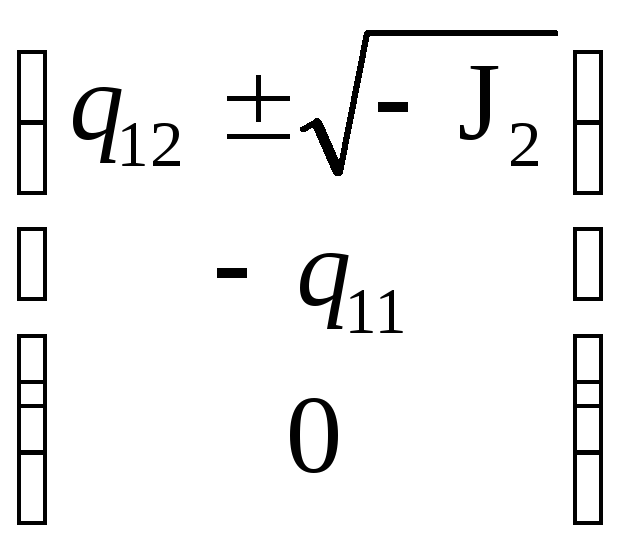_- - несобственные точки.

Задача. Найдите несобственные точки гиперболы и параболы, заданных каноническими уравнениями.

Решение. Парабола: у² = 2∙р∙х , перейдем к проективным координатам:

= 2∙р∙ |× х₃² х₂² - 2 р х₁∙х₃ = 0.

Найдем несобственные точки квадрики:

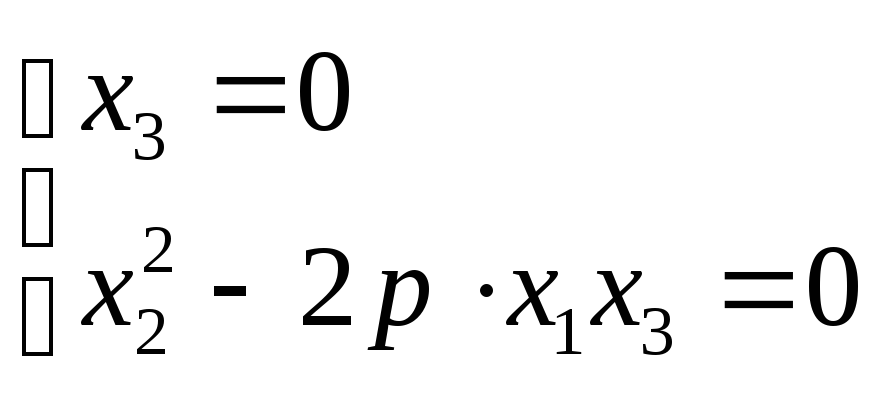
х₂² = 0 решение системы =Е_1∞ .

Матрицей квадрики будет - Q = .

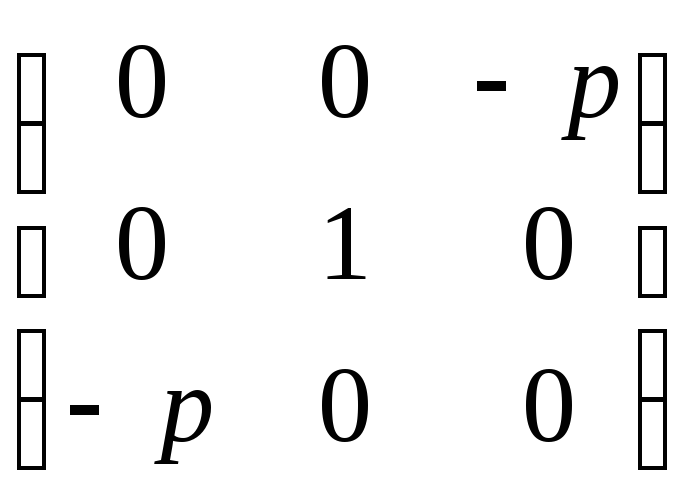Найдем поляру несобственной точки:

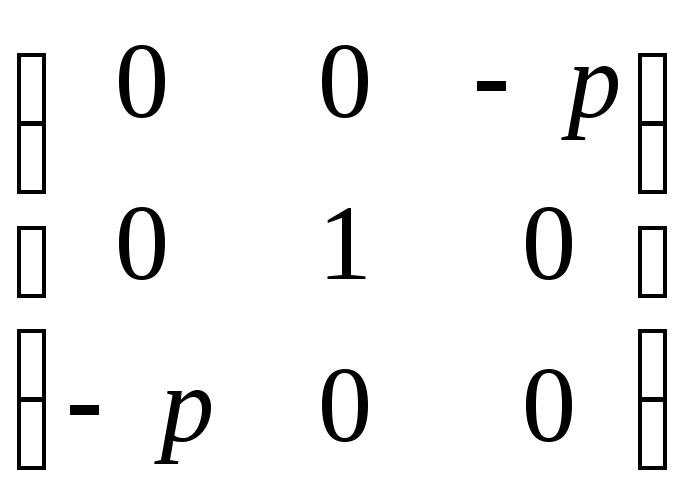= - р∙ х₃ = 0

х₃ = 0 – несобственная прямая (Е_1∞ Е_2∞).

Так как несобственная точка принадлежит квадрике, то поляра является касательной.

Для гиперболы - самостоятельно.

Определение: Асимптотой квадрики называется касательная в несобственной точке.

Таким образом, у эллипса нет асимптот (нет пересечения с несобственной прямой) у параболы одна асимптота – несобственная прямая у гиперболы две асимптоты.

Как известно эллипс и гипербола являются центральными линиями. Центр квадрики обычно определяется как точка, в которой делятся пополам все проходящие через нее хорды.

Будем рассматривать хорды не как отрезки, а как прямые.

Фиксируем какую-либо хорду, если центр – середина, тогда четвертая гармоническая точка будет несобственной и с силу гармонизма она будет принадлежать поляре центра. Но так как центр – середина для любой хорды, проходящей через центр, тогда поляра будет состоять из несобственных точек. Это дает основание для следующего определения:

Определение: Центром КВП называется полюс несобственной прямой.

Так как полюс находится по формуле: μ∙А= Q^-1 ∙а ^Т, тогда центр - μ∙А= Q^-1 ∙ ( 1 0 0 )^Т = Q^-1 ∙ .

На евклидовой плоскости диаметром КВП является хорда, проходящая через середины параллельных хорд. Но все параллельные прямые пересекаются в несобственной точке. Т.о. середины параллельных хорд гармонически сопряжены с этой несобственной точкой, а значит, они принадлежат поляре несобственной точки. Это позволяет дать следующее определение:

Определение: Диаметром квадрики будем называть поляру несобственной точки.

Замечание: Несобственных точек бесконечно много, а значит и диаметров много.

Уравнение диаметра: λ∙а∙Х = А_∞^Т∙Q∙Х

Замечание: По свойствам полюса и поляры – диаметры квадрики пересекаются в центре.

Задача. Определить аффинный класс квадрики, найти центр, асимптоты (если есть) х₁²+ х₂²+ х₃²+6∙х₁∙х₂ =0.

Найти диаметр, параллельный прямой 3 х₁+ 2 х₂ - х₃ = 0.

Решение. Найдем несобственные точки квадрики. Решим систему

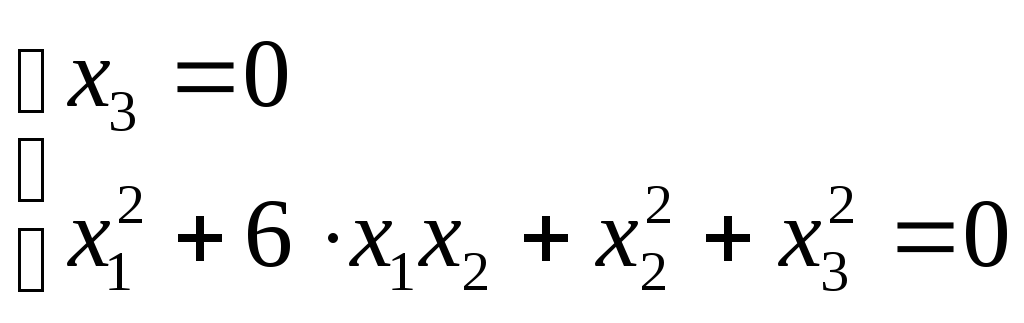
х₁²+ х₂²+6∙х₁∙х₂ = 0 | : х₂² ≠ 0 получим

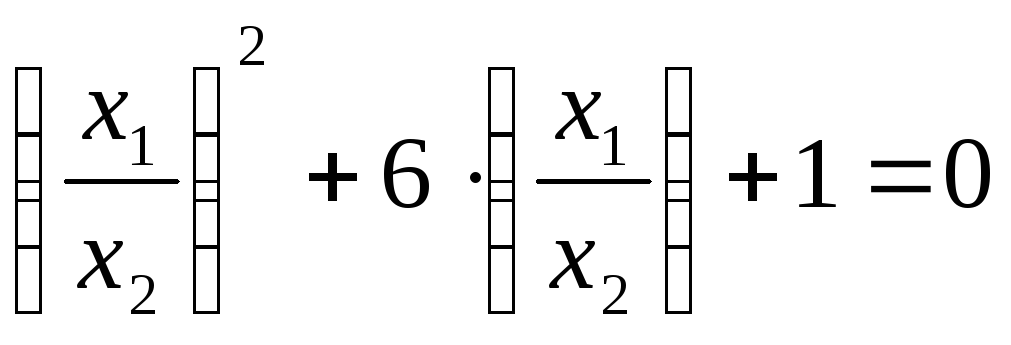
решение . Значит квадрика имеет две несобственные точки М₁ 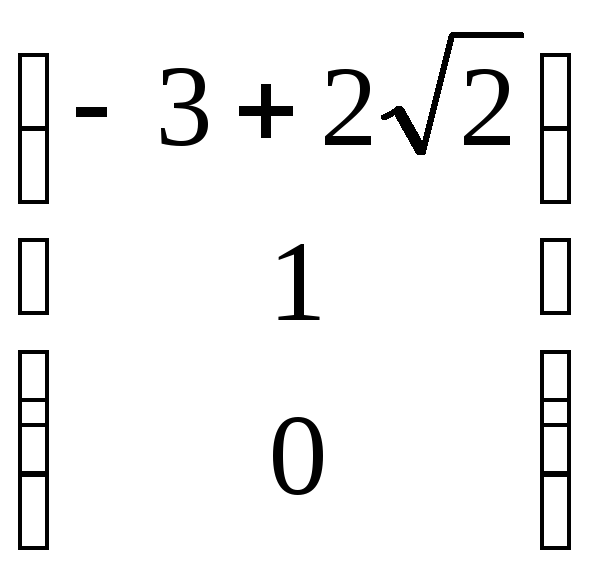и М₂ 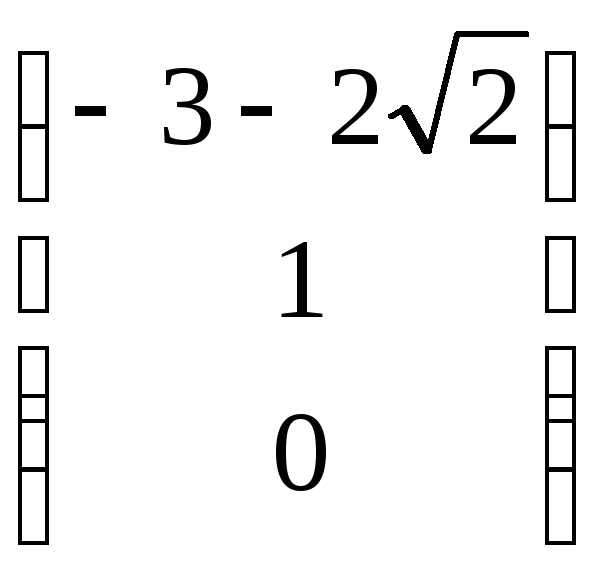, т.е. квадрика гиперболического типа.

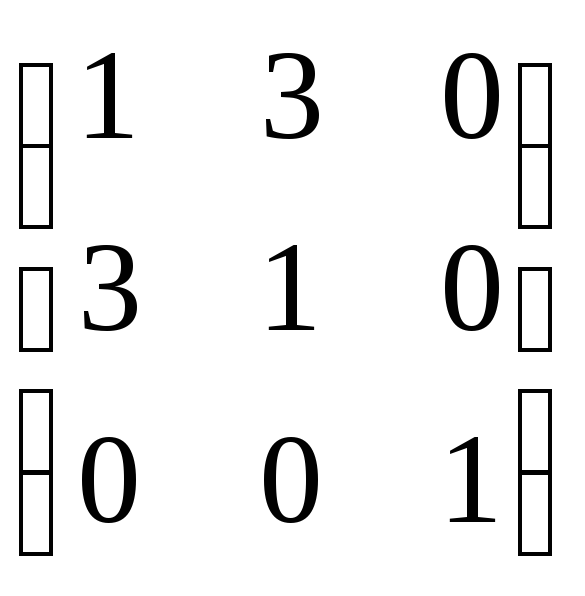
Матрицей квадрики будет - Q = 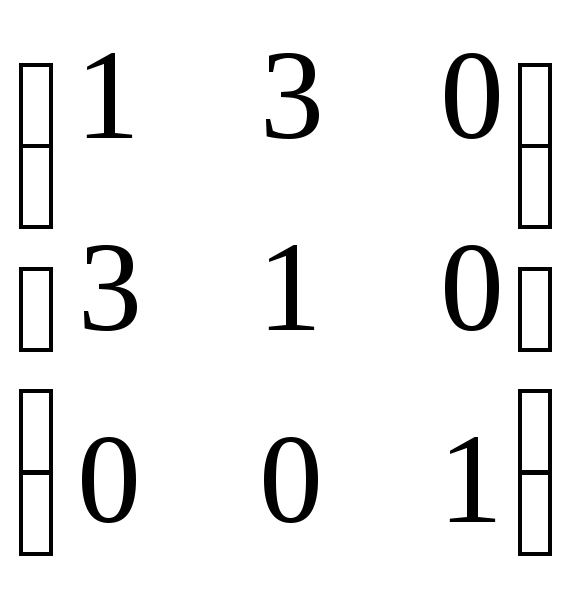, причем ΔQ= -8 ≠ 0, значит это не вырожденная линия. Таким образом, это гипербола. Найдем поляру несобственной точки:

= х₁ + 3х₂ = 0.

Q^-1=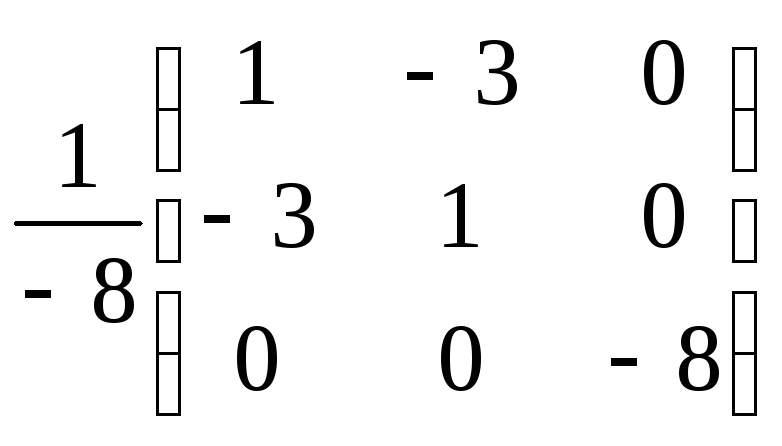, тогда полюс несобственной прямой х₃= 0

μ∙С= - центр квадрики.

Найдем асимптоты – поляры несобственных точек:

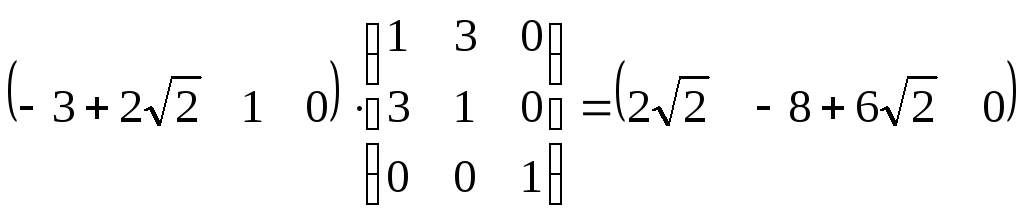
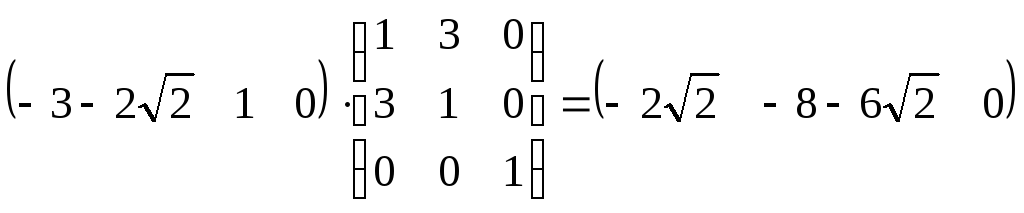
асимптоты имеют уравнения: и

Найдем несобственную точку прямой 3 х₁+ 2 х₂ - х₃ = 0 :

несобственная точка D .

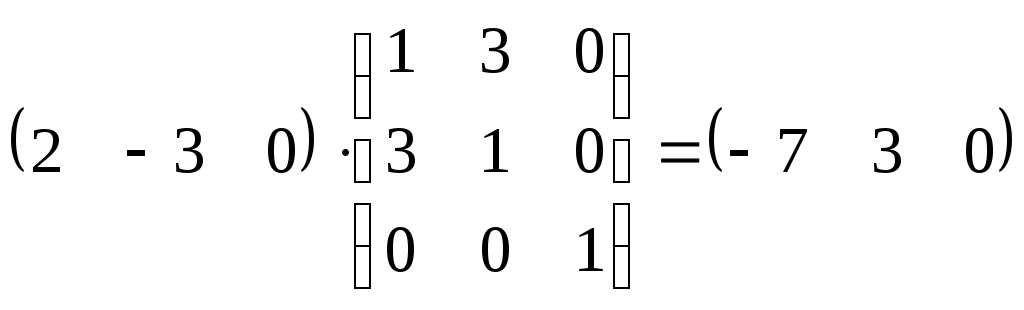
Диаметр соответствующий этой точке: 7 х₁ - 3 х₂ = 0.

Несобственная точка этого диаметра , тогда ее поляра:

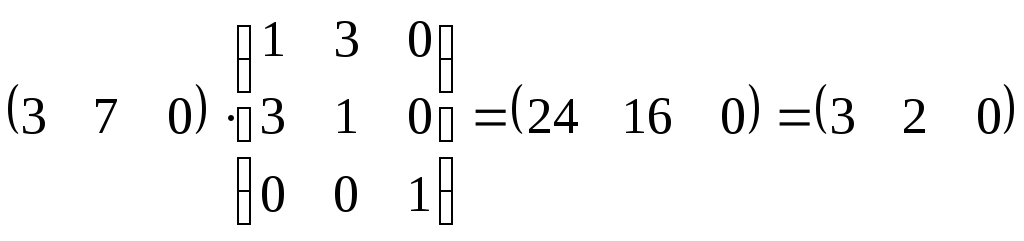
3 х₁ + 2 х₂ = 0.

Другой способ: искомый диаметр проходит через точку D и центр С:

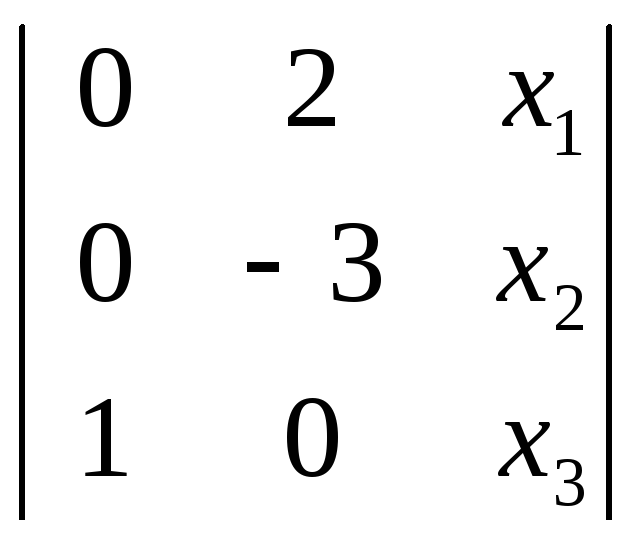=0 3 х₁ + 2 х₂ = 0.