Гомология

Определение: Не тождественная коллинеация, для которой существует точечно неподвижная прямая называется гомологией.

По принципу двойственности у гомологии будет неподвижная точка.

Определение: Прямая называется осью гомологии. Точка называется центром гомологии.

Обозначение: Р – центр, р – ось.

Определение: Если Р р - гомология называется параболической, если Р р - гомология называется гиперболической.

Теорема. Любая прямая инцидентная центру гомологии является неподвижной.

Доказательство. (самостоятельно).

Свойства:

1. Точка и ее образ лежат на одной прямой с центром А А′(АР).

2. Прямая и ее образ пересекаются на оси а а′ ∩ а = А₀ р.

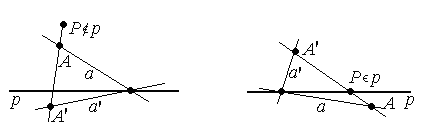
Теорема. Для любых точки Р, прямой р и пары точек А и А′, коллинеарных с точкой Р, существует единственная гомология с центром Р и осью р, переводящая А в А′.

(Сформулируйте теорему двойственную этой.)

Доказательство.

1 случай: Р р.

Пусть р ∩(АА′)=Х , возьмем ещё две точки U ≠ V р .

Р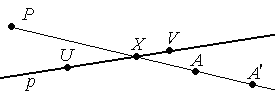ассмотрим две четвёрки точек: А, Р, U, V и А', Р, U, V – в каждой четвёрке точек никакие три не лежат на одной прямой. Тогда можно рассмотреть коллинеацию

φ: U→U, V→V, Р→Р, А→А′.

Так как U, V – неподвижные точки, тогда неподвижна вся прямая - р, а значит это гомология.

2 случай: Р р (самостоятельно). □

Вывод: Гомологию можно задать: осью, центром и парой точек, коллинеарных с центром. Гомологию можно задать: осью центром и парой прямых.

Построение образов и прообразов точек при гомологии.

1. Дано: Р р , А , А′ , Р – коллинеарны.

Простроить образ и прообразы произвольных точек.

а) М р → точки прямой р инвариантны.

б) В, С′ (АА′): (АВ)∩р=В₀ , (РВ)∩(В₀А′)=В′ - образ.

(А′С′)∩р=С₀ , (РС′)∩(С₀А)=С - прообраз.

в) К(АА′) → для таких точек вместо точек А и А′ можно использовать В , В′ или С , С′

(см (б)).

г) D_∞ → построение аналогично (б).

2. Дано: Р р , А , А′ , Р – коллинеарны.

Простроить образ и прообразы произвольных точек.

а) М р → точки прямой р инвариантны.

б) В, С′ (АА′): → (АВ)∩р=В₀ , (РВ)∩(В₀А′)=В′ - образ.

→ (А′С′)∩р=С₀ , (РС′)∩(С₀А)=С - прообраз.

в) К(АА′) → для таких точек вместо точек А и А′ можно использовать В , В′ или С , С′ (см (б)).

г) D_∞ → построение аналогично (б).

Замечание: Построения для параболической гомологии аналогичны построениям для гиперболической гомологии.

Рассмотрим гиперболическую гомологию, пусть Х= (АВ)∩(А′В′).

При центральном проектировании прямой (АА′) на прямую (ВВ′) с центром Х точки В, В′, В₀ являются центральными проекциями точек А, А′, А₀ . Точка Р при этом проектировании является неподвижной (почему?). Тогда по свойствам сложного отношения (РА₀ , АА′)=(РВ₀ ,ВВ′), значит это сложное отношение - величина постоянная.

Обозначим её h =(РА₀ , АА′) - она называется константой гомологии.

Теорема. Для любой прямой р, точки Р р, и любого действительного числа h, отличного от 0 и 1. Существует гиперболическая гомология с центром Р, осью р и константой h.

Доказательство. Дано Р р, h , берем А. А₀= р∩(АР) - точка единственна. Тогда точка А′ находится из условия h =(РА₀ , АА′) - по свойствам сложного отношения такая точка единственна, причем А′ (РА). По предыдущей теореме существует гомология с осью р, центром Р и А → А′. □

Определение: Гомология называется инволюционной, если она совпадает со своим обратным отображением.

Теорема. Параболическая гомология не может быть инволюционной.

Доказательство. От противного. Пусть Р р .

Так как преобразование - инволюция, то существуют точки А↔А′ и В↔В′. Тогда прямые (АВ)↔(А′В′) - переходят друг в друга, Q=(АВ)∩(А′В′)р. Прямые (А′В)↔(АВ′) – тоже переходят друг в друга, R=(А′В)∩(АВ′)р.

Но АВА′В′ - четырёхвершинник и ΔРQR – диагональный трёхвершинник, а значит эти точки не могут лежать на одной прямой (оси - р). (противоречие). □

Теорема. Для того чтобы гиперболическая гомология была инволюционной, необходимо и достаточно, чтобы константа h =-1.

Доказательство. Пусть Р р , М → М′ , (ММ′)∩р=М₀ .

Необходимость h = -1.

Пусть М′→М′′, тогда (РМ₀ ,ММ′)= - 1 =(РМ₀ ,М′М) - по свойству сложного отношения,

но (РМ₀ , М′М)=( РМ₀ , М′′М′) - по свойству проективного преобразования М=М′′ М ↔ М′.

Достаточность М ↔ М′.

(РМ₀ , ММ′)= (РМ₀ ,М′М)² = 1 (РМ₀ ,М′М)=± 1.

Но (РМ₀ ,М′М)=1 - не может быть (почему?), (РМ₀ ,М′М) = - 1. □

Вывод: Инволюционная гомология определяется центром и осью.