Уравнение прямой. Координаты прямой

Пусть даны две различные точки А и В, по свойствам проективного плоскости (пространства) через две различные точки проходит одна и только одна прямая - (АВ).

Пусть точка Х (АВ), тогда по условию коллинеарности трёх точек

= λ∙+ μ∙ или Х=λ ∙А+ μ∙В.

Определение: Уравнение Х=λ ∙А+ μ∙В называется параметрическим уравнением прямой (АВ). Величины λ и μ называются параметрами точки Х.

Для точки А - λ=1 и μ=0, для точки В - λ=0 и μ=1.

Замечание: Параметры точки не могут одновременно обращаться в ноль. Кроме того, параметры определяются с точностью до пропорциональности. (Почему?)

Замечание: Параметрическое уравнение применимо для задания прямой в Р₃ и в Р_п .

Задача. Даны две точки А и В, записать параметрическое уравнение прямой, найти значения параметров для точек М и К ,

Решение. Параметрическое уравнение прямой имеет вид: Х=λ∙А+ μ∙В

или = λ∙+ μ∙, или .

Чтобы найти параметры для точки М нужно решить систему ,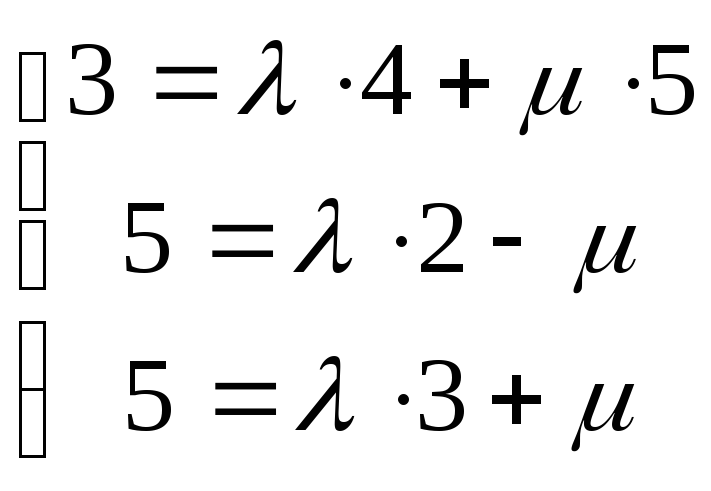

решение системы: λ=2 и μ= -1, значит точка М (АВ).

Чтобы найти параметры для точки К нужно решить систему ,

система не имеет решения, значит точка К(АВ).

Рассмотрим другое условие коллинеарности точек: = 0.

Разложим этот определитель по третьему столбцу:

х₁∙ - х₂∙+ х₃∙ = 0.

Обозначим: и₁ = , и₂ = - , и₃ = .

Тогда получим уравнение: и₁ х₁ + и₂ х₂ + и₃ х₃ = 0.

Среди чисел и₁, и₂, и₃ хотя бы один коэффициент отличен от нуля. (Почему?)

Теорема. Однородное линейное уравнение степени от трех переменных на проективной плоскости определяет прямую линию.

Доказательство. Пусть и₁ х₁+ и₂ х₂+ и₃ х₃= 0 - уравнение некоторой линии, докажем, что это прямая. Хотя бы один коэффициент уравнения не равен 0. Пусть для определенности и₁ ≠ 0.

Рассмотрим точки М и К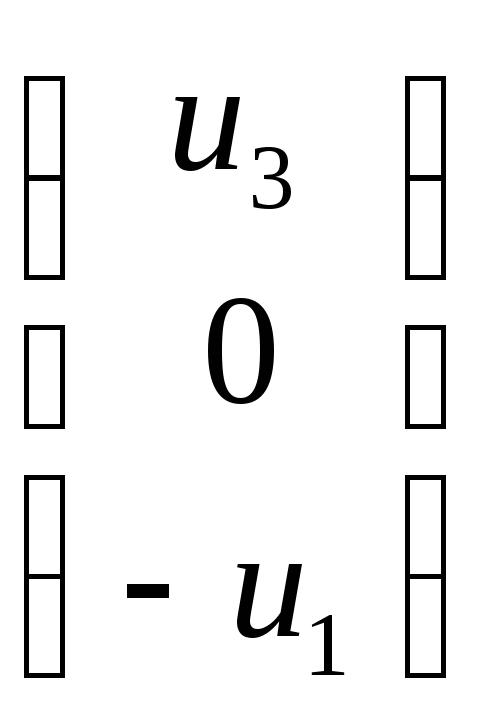, эти точки существуют, различны и лежат на этой линии.

(Почему?).

Составим уравнение прямой (МК):

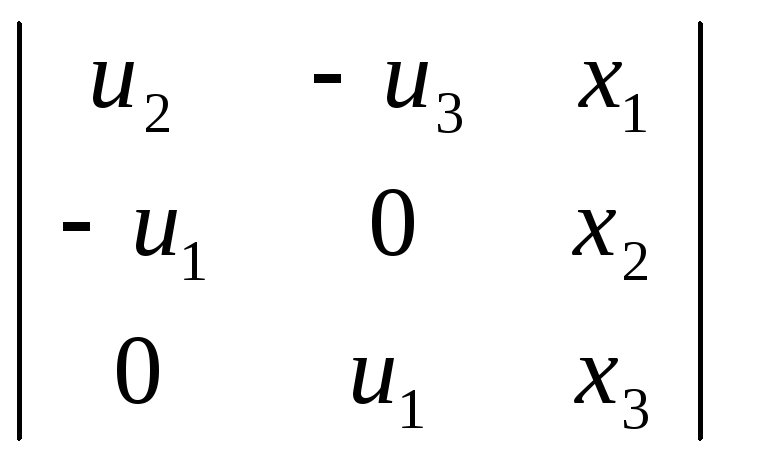= 0 - и²₁ ∙х₁ - и₁ ∙и₂ ∙х₂ - и₁ ∙и₃ ∙х₃ = 0 | : и₁≠0,

получим уравнение и₁ х₁ + и₂ х₂ + и₃ х₃ = 0.

Таким образом, уравнение линии, проходящей через точки М и К совпадает с уравнением прямой (МК), значит это линия и есть прямая. □

Замечание: Так как уравнение однородное, то его коэффициенты определены с точностью до пропорциональности.

Определение: Однородное уравнение I степени от трех переменных на проективной плоскости называется однородным уравнением прямой.

Задача. Даны точки А и В , составить однородное уравнение прямой, проверить принадлежат ли точки М и К этой прямой.

Решение. 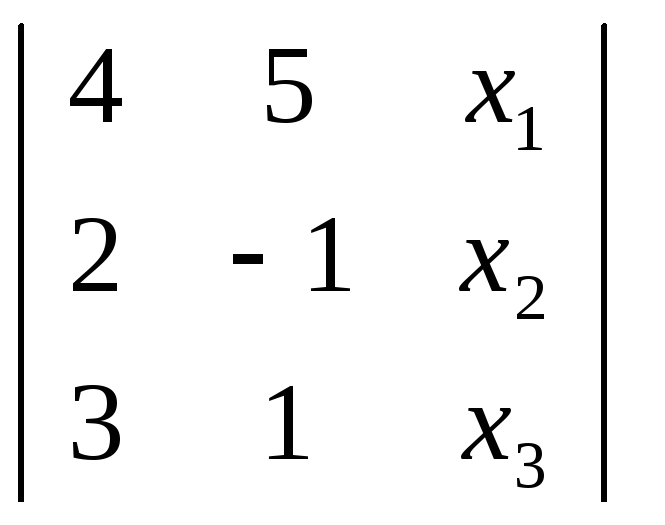=0 х₁ -х₂+ х₃= 0

5 х₁ – (-11) х₂+(-14) х₃ = 0 5 х₁ + 11 х₂ - 14 х₃ = 0.

Подставим координаты точек М и К в уравнение прямой:

5∙3 + 11∙5 - 14∙5=15 + 55 – 70 = 0 М (АВ),

5∙1 + 11∙(-3) - 14∙2 = 5 – 33 – 28 ≠ 0 К (АВ).

Взаимное расположение двух прямых

Рассмотрим две прямые заданные однородными уравнениями.

и : и₁ х₁+ и₂ х₂+ и₃ х₃ =0 и v : v₁ х₁+ v₂ х₂+ v₃ х₃ =0.

Найдем общие точки. Для этого надо решить систему линейных уравнений:

.

Из курса алгебры известно, что число линейно-независимых решений однородной системы зависит от ранга матрицы системы и равно число неизвестных минус ранг матрицы.

Пусть r = rg, тогда r { 0, 1, 2}.

Случай r = 0 невозможен, так как хотя бы один коэффициент в каждом уравнении отличен от нуля.

Случай r = 1 означает, что строки матрицы пропорциональны, т.е. мы имеем одно и то же уравнение, что означает - прямые совпадают.

При r = 2 , число линейно-независимых решений 3 – 2 = 1, т.е. одно линейно-независимое решение, которое дает одномерное линейное подпространство L₁ которое в свою очередь порождает Р₀ – проективную точку. Это означает, что прямые пересекаются в одной точке. Других вариантов нет.

Замечание: Тем самым мы доказали, что любые две различные прямые пересекаются в одной точке.

Замечание: Одним из решений однородной системы из двух уравнение от трёх неизвестных будет:

х₁=; х₂= ; х₃=.

Вывод: Прямая на проективной плоскости (так же как и точка) определяется набором чисел - и₁ , и₂ , и₃ , с точностью до пропорциональности, которые одновременно не обращаются в ноль.

Определение: Числа ( и₁ : и₂ : и₃ ) называются координатами прямой.

Замечание: Договоримся в дальнейшем записывать координаты точек в виде матрицы-столбца, а координаты прямых в виде матрицы-строки.

Тогда, если Х - точка, а и ( и₁ и₂ и₃ ) - прямая, то однородное уравнение прямой можно записать в матричном виде: (и₁ и₂ и₃)∙=0 или и∙Х=0.

Задача. Определить взаимное расположение прямых:

l : 2 х₁ - х₂+ х₃ =0 и т : х₁+ 3 х₂ - 2 х₃ =0.

Решение. Координаты прямых будут ( 2 -1 1 ) и ( 1 3 -2 ) , так как они не пропорциональны, значит прямые различны, а следовательно они пересекаются в одной точке. Найдем эту точку:

→ (у второй координаты меняем знак!).