
- •Аналитическое представление проективных преобразований 71
- •Дополнительная литература 91 введение
- •Структурно-логическая схема курса «проективная геометрия»
- •Исторические сведения
- •Проективное пространство
- •Аксиомы проективного пространства
- •Модели проективной прямой, проективной плоскости
- •Изоморфизм моделей
- •Проективная система координат
- •Проективный репер
- •Координаты точки на прямой (плоскости)
- •Принадлежность трёх точек одной прямой
- •Однородные проективные координаты
- •Уравнение прямой. Координаты прямой
- •Взаимное расположение двух прямых
- •Принадлежность трёх прямых одному пучку
- •Координаты точки и уравнение прямой в пространстве
- •Преобразование координат
- •Принцип двойственности
- •Теорема Дезарга
- •Простое отношение
- •Сложное отношение
- •Гармонизм
- •Гармонические свойства полного четырехвершинника
- •Квадрики на проективной плоскости
- •Классификация кривых второго порядка на проективной плоскости.
- •Взаимное расположение прямой и квадрики
- •Уравнение касательной
- •Полюс и поляра
- •Теорема Штейнера
- •Теорема Паскаля и ее предельные случаи
- •Задачи на построение, связанные с овалом
- •Прямые и квадрики на расширенной евклидовой плоскости
- •Проективные преобразования
- •Проективные преобразования плоскости
- •Аналитическое представление проективных преобразований
- •Перспектива
- •Отображение пучка в пучок
- •Инволюция
- •Коллинеация
- •Инварианты коллинеации
- •Гомология
- •Гомологии на расширенной плоскости
- •Дополнительная литература
Принадлежность трёх прямых одному пучку
Рассмотрим три прямые l : и1 х1+ и2 х2+ и3 х3 = 0,
т : v1 х1+ v2 х2+ v3 х3 = 0,
п : w1 х1+ w2 х2+ w3 х3 =0.
Если l ∩ m ∩ n = А, то у однородной системы линейных уравнений должно существовать одно не нулевое решение (с точностью до пропорциональности), т.е. подпространство решений состоит из одного вектора
1 = 3
– rg
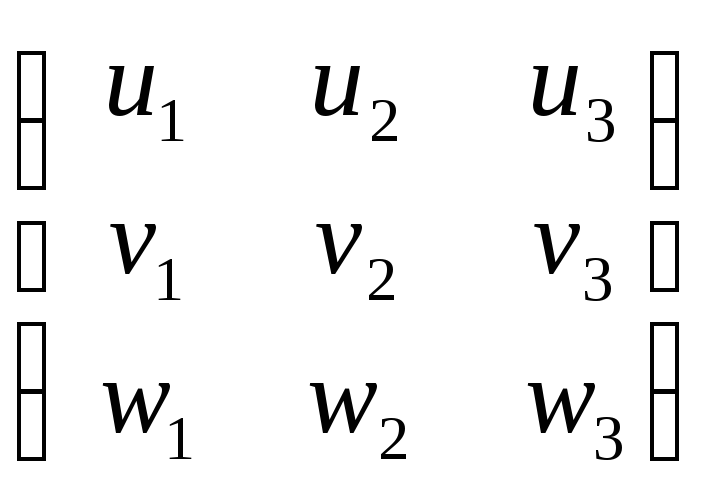
![]() rg
rg
 = 2,
= 2,
это означает, что одна строка является линейной комбинацией других: w = λ∙и + μ∙v - параметрическое уравнение пучка прямых. (сравнить с коллинеарностью трех точек Х = λ∙А + μ∙В ).
Координаты точки и уравнение прямой в пространстве
Рассмотрим п –мерное проективное пространство Pп.
Определение: Е1 , Е2 ,…, Еп+1 , Е - упорядоченная система различных точек среди которых никакие три не лежат на одной прямой (Р1), никакие четыре не лежат на одной плоскости (Р2), никакие пять не принадлежат (Р3), и т.д. называется проективным репером в пространстве Pп.
Обозначение: R(Е1, Е2, …, Еп+1, Е) - проективный репер на прямой.
Названия: Е1, Е2,… , Еп+1 - вершины репера или базисные точки,
Е - единичная точка,
(Е1Е2), (Е1Е3), …, (ЕпЕп+1) - координатные прямые.
Проективное пространство Pп порождается Vп+1.
Пусть Е1,
Е2,…,
Еп+1,
Е
порождаются - ē1
, ē2
,…, ēп+1
, ē
![]() Vп+1.
Vп+1.
Векторы ē1 , ē2 ,…, ēп+1 – линейно независимы (почему?), а значит могут быть базисом в Vп+1.
Определение: Система векторов ē1 , ē2 , ,…, ēп+1 , ē - называется согласованной,
если ē1+ē2 +…+ ēп+1 =ē.
Пусть ē1,
ē2,
,…, ēп+1
, ē -
согласованная система векторов и пусть
точка М![]() Pп
порождается вектором
Pп
порождается вектором
![]() ,
тогда
,
тогда ![]() =
х1∙ē1+
х2∙ē2
+…+ хп+1
∙ēп+1
=
х1∙ē1+
х2∙ē2
+…+ хп+1
∙ēп+1
Определение: Набор чисел ( х1 : х2 : … : хп+1 ) называется координатами точки в данном репере.
По аналогии с проективной прямой и проективной плоскостью, координаты точки в Pп определяются с точностью до пропорциональности.
Точки могут лежать на одной прямой или не лежать на одной прямой.
1. А,
В, С
![]() P1
, тогда
векторы
P1
, тогда
векторы
![]() ,
,
![]() ,
,
![]()
![]() L2
L2
![]()
![]() ,
,
![]() ,
,
![]() - линейно-зависимы
- линейно-зависимы
![]()
![]() α,
β
такие, что
α,
β
такие, что
![]() = α∙ā
+ β∙
= α∙ā
+ β∙
![]()
![]()
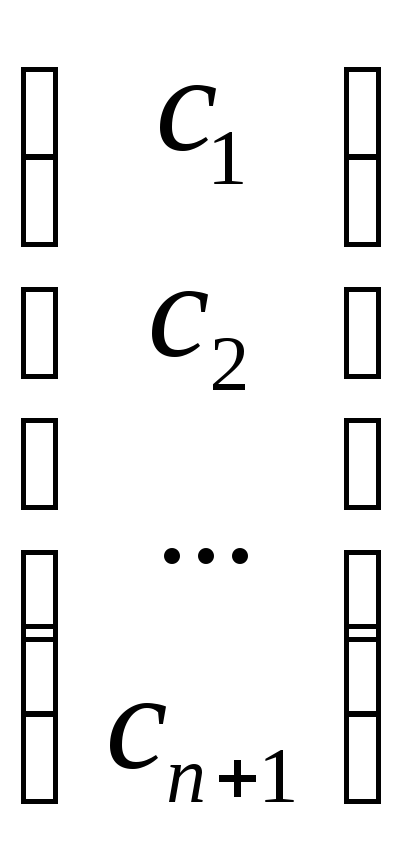 =α∙
=α∙ +
β∙
+
β∙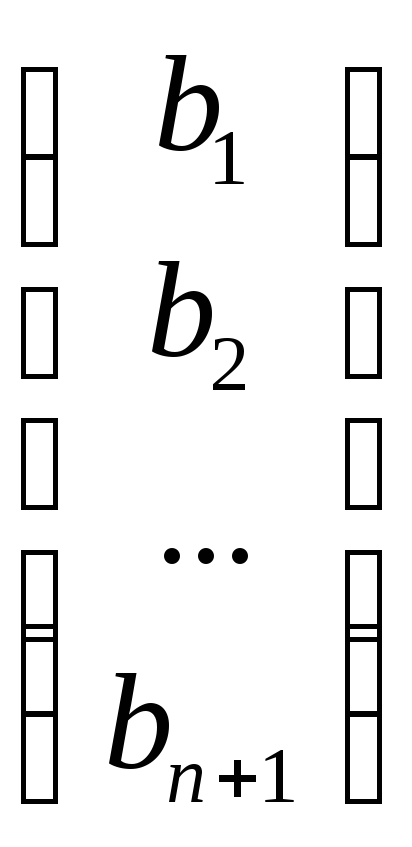 ,
или rg
,
или rg =
2.
=
2.
2. А,
В
![]() P1
и С
P1
и С
![]() P1
, тогда
векторы
P1
, тогда
векторы
![]() ,
,
![]() ,
,
![]()
![]() L2
L2
![]()
![]() ,
,
![]() ,
,
![]() - линейно-независимы
- линейно-независимы
![]()
![]() ≠
α∙
≠
α∙![]() +
β∙
+
β∙![]()
![]()
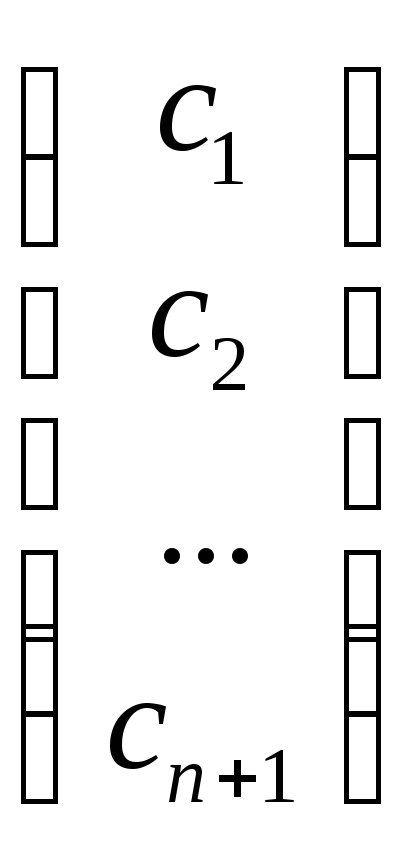 ≠
α∙
≠
α∙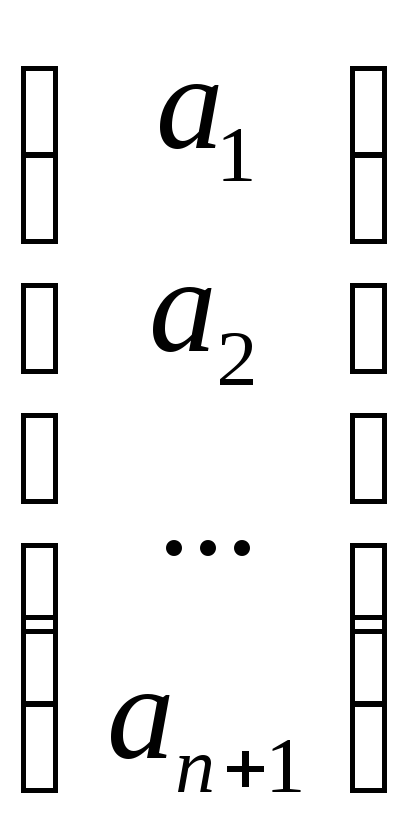 +
β∙
+
β∙ ,
или rg
,
или rg ≠
2.
≠
2.
Пусть даны две
различные точки А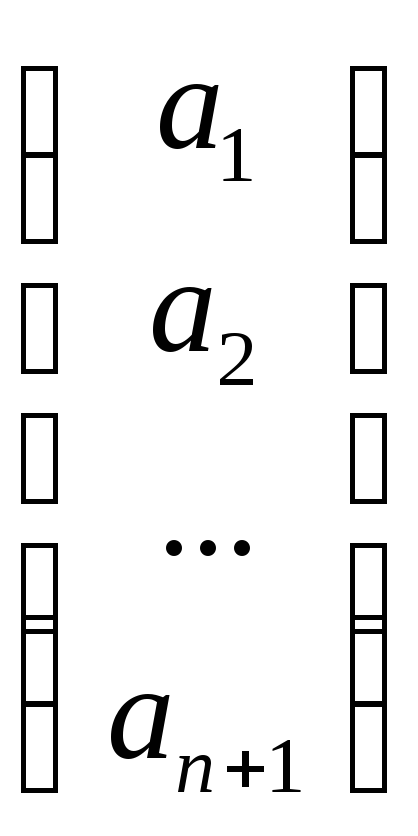 и В
и В ,
по свойствам Рп
через две
различные точки проходит одна и только
одна прямая - (АВ).
,
по свойствам Рп
через две
различные точки проходит одна и только
одна прямая - (АВ).
Пусть точка Х
![]()
![]() (АВ),
тогда
(АВ),
тогда
 =
λ∙
=
λ∙ +
μ∙
+
μ∙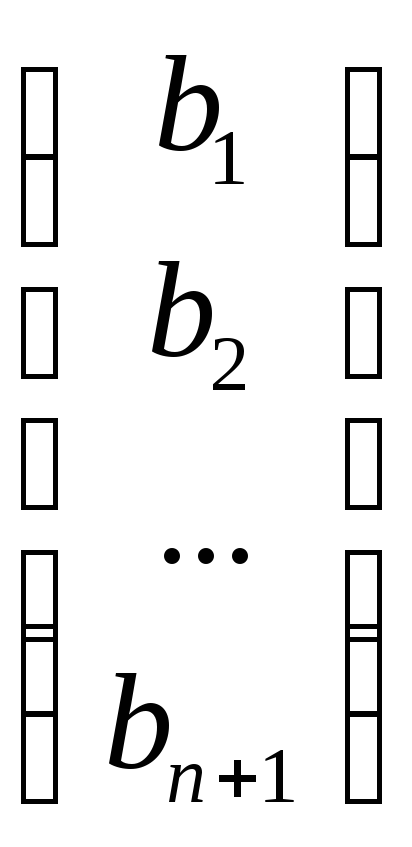 или Х=λ∙А+
μ∙В
– параметрическое
уравнение прямой в пространстве.
или Х=λ∙А+
μ∙В
– параметрическое
уравнение прямой в пространстве.
Замечание: В проективном пространстве прямая может задаваться только параметрическим уравнением (сравнить с заданием прямой в евклидовом пространстве).
Однородное уравнение вида и1 х1+ и2 х2+…+ ип+1 хп+1 = 0 не будет задавать прямую.
Преобразование координат
Рассмотрим проективную прямую Р1 и два репера
R(Е1 ,Е2 ,Е) и R′(Е′1 ,Е′2 , Е′). Пусть известны координаты точек второго репера в первом репере:
Е′1
![]() ,
Е′2
,
Е′2![]() ,
Е′
,
Е′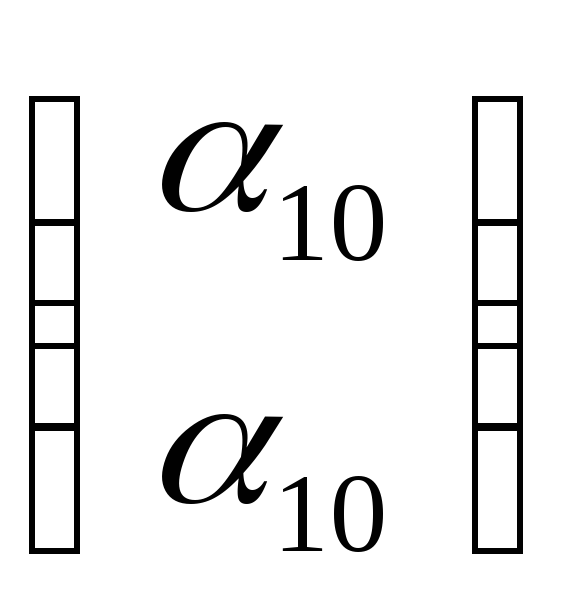 , т.е. ē′1
= α11
ē1+
α21
ē2,
ē′2 =
α12
ē1
+ α22
ē2
, ē′ = α10
ē1
+ α20
ē2
.
, т.е. ē′1
= α11
ē1+
α21
ē2,
ē′2 =
α12
ē1
+ α22
ē2
, ē′ = α10
ē1
+ α20
ē2
.
В общем случае
репер R′(Е′1
,Е′2
,Е′)
может оказаться не согласованным (ē′1+
ē′2 ≠
ē′). Согласуем
точки второго репера, т.е. найдем такие
числа k1
и k2
, что ē′
= k1ē′1
+ k2ē′2
, для этого
необходимо решить систему:
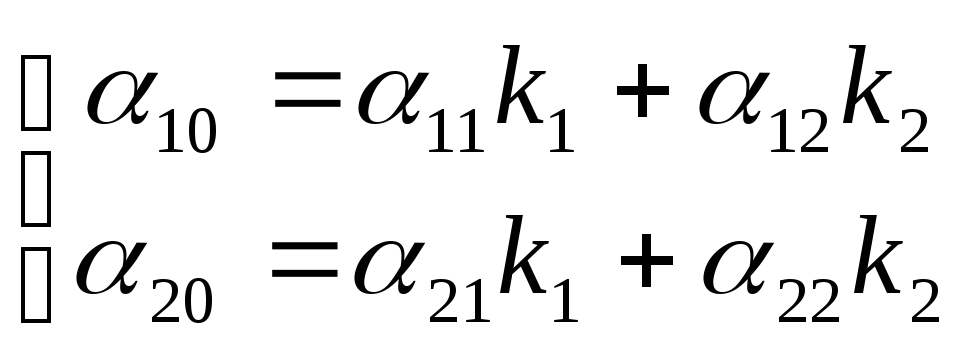 .
.
Пусть матрица
системы А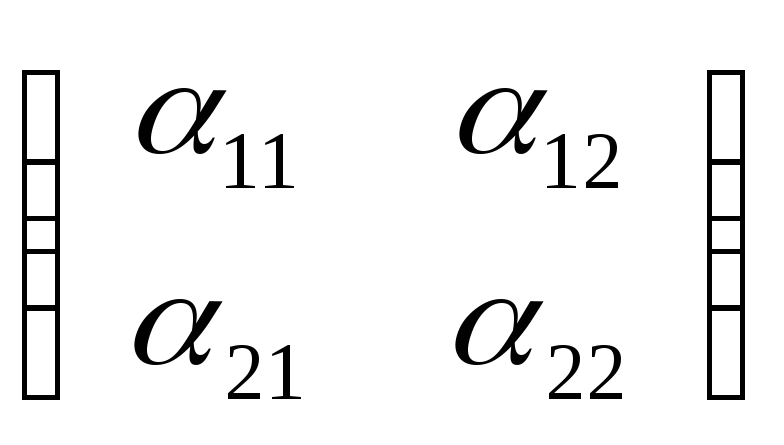 ,
тогда ∆А≠0
(почему?).
,
тогда ∆А≠0
(почему?).
Система имеет
единственное решение (k1
, k2)
и тогда будем считать координатами
точек Е′1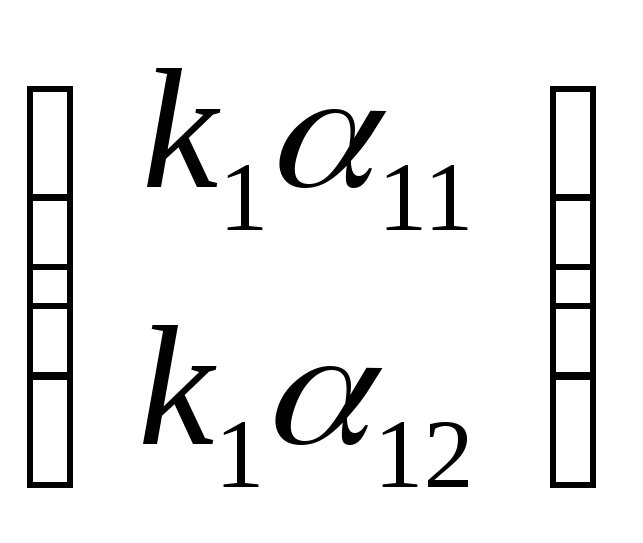 и Е′2
и Е′2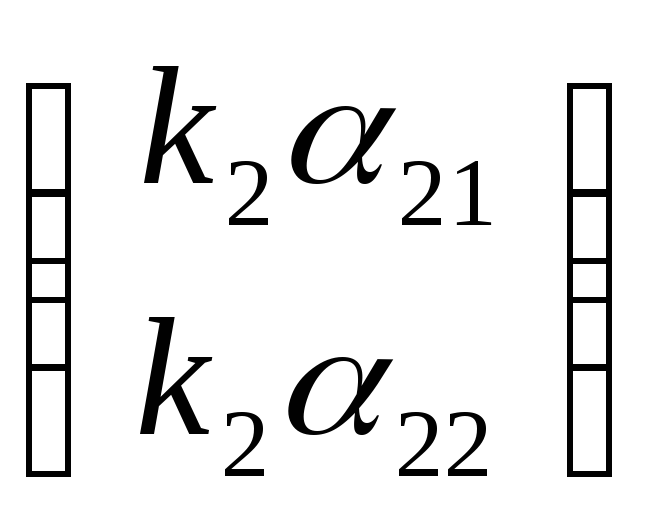 ,
репер в этом случае будет согласованным.
,
репер в этом случае будет согласованным.
Замечание: В дальнейшем будем считать, что второй репер – согласован (если нет, то мы знаем, как его согласовать).
Пусть точка Х
![]() в репере R
и та же точка в репере R′
имеет координаты
в репере R
и та же точка в репере R′
имеет координаты
![]() .
.
Тогда вектор
![]() ,
порождающий эту точку может выражаться
через вектора первого и второго базисов:
,
порождающий эту точку может выражаться
через вектора первого и второго базисов: ![]() = х1
∙ē1
+ х2
∙ē2
или
= х1
∙ē1
+ х2
∙ē2
или
![]() = у1∙ē′1
+ у2∙ē′2
= у1∙ē′1
+ у2∙ē′2
![]()
![]() =
у1∙ē′1
+ у2∙ē′2
= у1∙(α11∙ē1
+ α21∙ē2)+
у2∙(α1∙ē1
+ α22∙ē2)
= =(у1∙α11+
у2∙α12)∙ē1+
(у1∙α21+
у2∙α22)∙ē2
=
х1∙ē1+
х2∙ē2
=
у1∙ē′1
+ у2∙ē′2
= у1∙(α11∙ē1
+ α21∙ē2)+
у2∙(α1∙ē1
+ α22∙ē2)
= =(у1∙α11+
у2∙α12)∙ē1+
(у1∙α21+
у2∙α22)∙ē2
=
х1∙ē1+
х2∙ē2
![]() х1
= у1∙α11
+
у2∙α12
и х2
=
у1∙α21
+ у2∙α22
,
х1
= у1∙α11
+
у2∙α12
и х2
=
у1∙α21
+ у2∙α22
,
или
![]() =
=
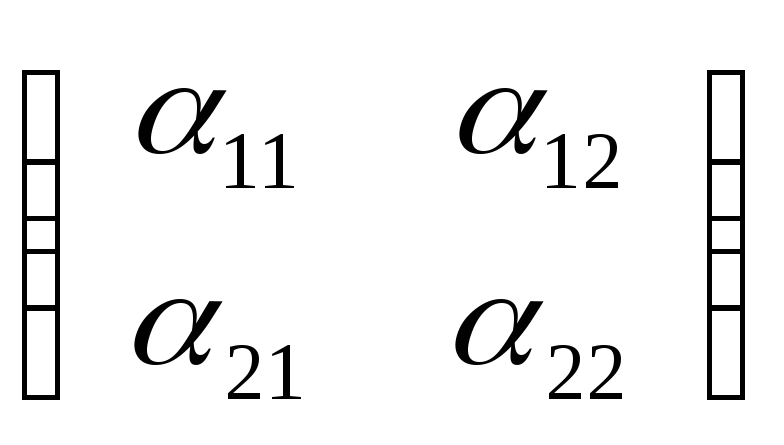 ∙
∙![]() ,
в матричной записи: ХR
=A∙XR′
,
,
в матричной записи: ХR
=A∙XR′
,
где ХR - столбец координат точки Х в первом (старом) репере,
а XR′ - столбец координат той же самой точки Х во втором (новом) репере.
Матрица А будет
матрицей перехода от старого репера к
новому реперу.
будет
матрицей перехода от старого репера к
новому реперу.
Замечание: Матрица А является невырожденной. (Почему?).
Вывод: Зная матрицу перехода и координаты точки в новом репере можно находить координаты точки в старом репере:
ХR =A∙XR′ │∙А-1 слева
А-1
∙ ХR
= А-1∙A∙XR′
= XR′
![]() XR′
= А-1
∙ ХR
.
XR′
= А-1
∙ ХR
.
Вывод: Формулы преобразования координат точек при переходе к другому реперу имеют вид:
λ ХR =A∙XR′ и μ XR′ = А-1 ∙ХR .
Аналогичные рассуждения можно применить для Р2,
Пусть Е'1![]() ,
Е'2
,
Е'2![]() ,
Е'3
,
Е'3 ,
Е'
,
Е'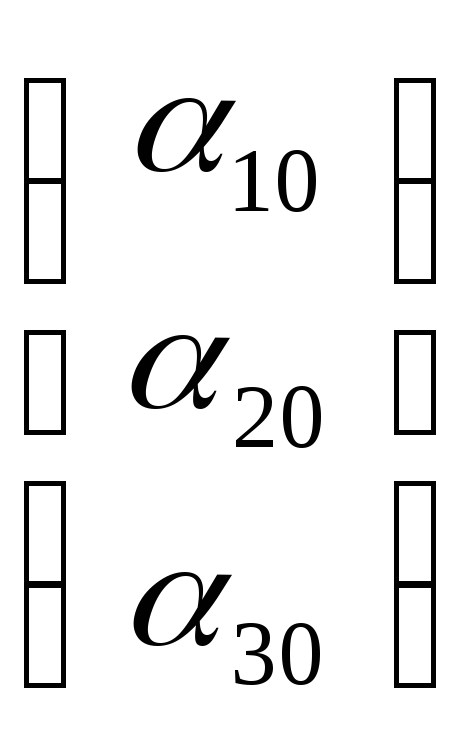 .
.
Для согласования второго репера будем находить k1 , k2 , k3 .
Получим матрицу третьего порядка А.
Формулы преобразования координат точек будут такими же:
λ ХR =A∙XR′ и μXR′ = А-1∙ХR .
Рассмотрим прямую и∙Х=0.
Пусть её координаты в старом репере - иR и в новом - uR′ .
Уравнение прямой в старом репере иR ∙ХR=0, в новом иR′ ∙ХR′=0.
Подставим формулы преобразования координат, получим 0= иR∙ХR = иR∙A∙XR′ = иR′ ∙ХR′ ,
где иR∙A=иR′ или λ иR′= иR∙A, тогда μ иR = иR′ ∙A-1 .
Вывод: Формулы преобразования координат точек и прямых на проективной плоскости имеют вид:
Для точек λ ХR =A∙XR′ и μ XR′ = A -1 ∙ХR .
Для прямых λ иR′= иR ∙ A и μ иR = иR′ ∙ A -1.
Замечание: Обратите внимание на умножение матриц: для точек матрица перехода умножается слева, а для прямых справа.
Задача. Даны два репера R(Е1 , Е2 , Е3 , Е) и R′(Е′1 , Е′2 , Е′3 , Е′). Известны координаты точек второго репера в первом:
Е′1
![]() ,
Е′2
,
Е′2![]() ,
Е′3
,
Е′3![]() ,
Е′
,
Е′![]() .
.
Найти формулы
преобразования координат при переходе
от одного репера к другому. Найти
координаты точки М
во втором репере если известны её
координаты в первом МR
![]() .
Найти координаты точки К
в первом репере если известны её
координаты во втором КR
′
.
Найти координаты точки К
в первом репере если известны её
координаты во втором КR
′
![]() .
.
Найти уравнение прямой а : 5 х1 - 2 х2+3 х3 = 0 в новом репере.
Решение. Проверим, согласованы ли точки второго репера:
![]() +
+![]() +
+![]() =
=![]() ≠
≠![]() - второй репер не согласован.
- второй репер не согласован.
Согласуем его, для
этого решим систему
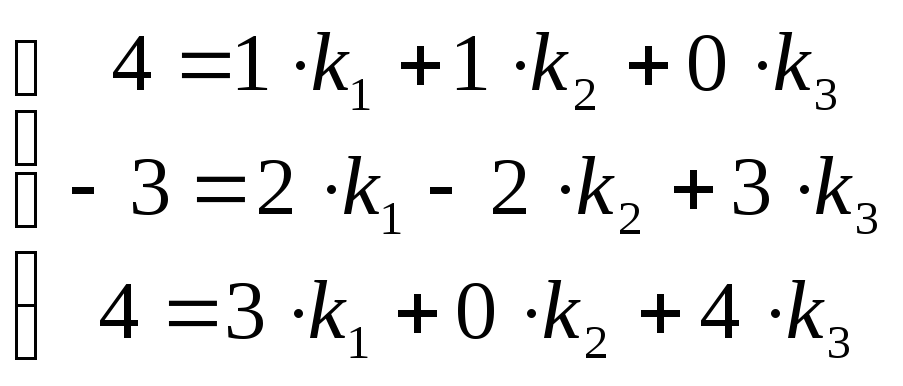 ,
,
её решением будет: k1 = 2, k2 = 2, k3= -1,
тогда матрица
перехода будет A
 ,
,
обратной
является A-1=![]()
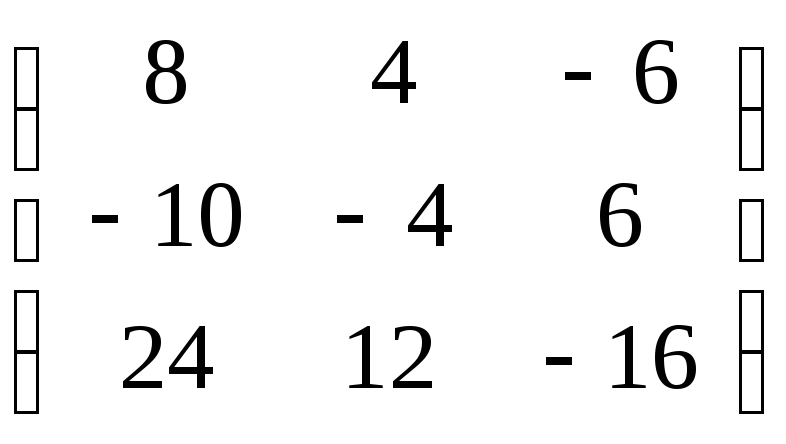 =
=![]()
 .
.
Так как координаты
определяются с точностью до
пропорциональности коэффициент
![]() можно отбросить.
можно отбросить.
Формулы преобразования координат примут вид:
λХR= ∙XR′
и μXR′
=
∙XR′
и μXR′
= ∙ХR
.
∙ХR
.
μМR′
= A
-1 ∙МR
= ∙
∙![]() =
= .
.
λКR=
A
∙КR′
= ∙
∙![]() =
= ,
с учетом пропорциональности координаты
точки К в
старом репере будут
,
с учетом пропорциональности координаты
точки К в
старом репере будут
![]() .
.
λ аR′=
аR∙A
=![]() ∙
∙ =
=![]() ,
с учетом пропорциональности координаты
прямой будут
,
с учетом пропорциональности координаты
прямой будут
![]()
![]() аR′
: 10
х′1 +
9
х′2
= 0
аR′
: 10
х′1 +
9
х′2
= 0
