Коллинеация

Определение: Проективное преобразование плоскости называется коллинеацией, если образом точки будет точка, а образом прямой прямая.

Свойства:

1. Сохраняется инцидентность точек и прямых.

2. Сохраняется сложное отношение четырёх точек, лежащих на одной прямой и четырёх прямых пучка.

3. Композиция коллинеаций, есть коллинеация.

4. Множество коллинеаций образует подгруппу в группе проективных преобразований.

Доказательство. Самостоятельно.

Теорема 1. Пусть А₁, В₁, С₁, D₁ и А₂, В₂, С₂, D₂ - упорядоченные четверки точек, в каждой из которых никакие три не лежат на одной прямой. Тогда существует коллинеация φ на проективной плоскости такая, что: φ(А₁) = А₂, φ(В₁) =В₂, φ(С₁) = С₂, φ(D₁) = D₂.

Доказательство. По аналогии с проективным отображением прямой на прямую, преобразование плоскости можно разложить на композицию не более чем трёх перспектив. Доказательство осуществляется построением. □

Рассмотрим Р₂ и два репера, тогда уравнение коллинеации, переводящее точки репера в точки репера единственное и задается формулами (**).

Пусть и ( и₁ : и₂ : и₃ ) - прямая и∙Х = 0, её образ - f (и) = и ′ (и′₁ : и′₂ : и′₃) → и′∙Х ′ = 0 .

и∙Х = и∙А^-1 ∙f (Х) = и∙ А^-1 ∙Х ′ = 0 → и∙А^-1 = λ∙и′ μ∙и = и′∙А.

Вывод: Формулы коллинеации имеют вид:

Для точек: λ∙Х ′= А∙Х и μ∙Х = А^-1∙Х ′.

Для прямых: и∙А^-1 = λ∙и′ μ∙и = и′∙А.

Замечание: Формулы очень похожи на формулы преобразования координат при переходе к другому реперу. Но там координаты одной и той же точки в разных реперах, здесь координаты разных точек (образа и прообраза) в одном репере.

Инварианты коллинеации

Определение: Точка называется неподвижной (инвариантной) точкой проективного преобразования, если она переходит сама в себя.

Определение: Прямая называется неподвижной (инвариантной) прямой проективного преобразования, если она переходит

сама в себя.

Определение: Прямая называется точечно неподвижной (точечно инвариантной) прямой проективного преобразования, если каждая точка этой прямой инвариантна.

Нахождение инвариантов коллинеации.

Так как для инвариантных точек λ∙Х = М∙Х , то они являются собственными векторами матрицы преобразования. Собственные значения находятся из характеристического уравнения

det | М – λ ∙Е | = 0.

Матрица коллинеации - третьего порядка, а значит, характеристическое уравнение будет кубическим. При решении кубического уравнения возможны случаи:

• 1 случай. λ₁ , λ₂ – комплексные, λ₃ – действительные корни.

λ₃ – дает одну инвариантную точку и в силу принципа двойственности будет одна инвариантная прямая.

• 2 случай. λ₁ , λ₂ , λ₃ – различные действительные корни.

Тогда собственные вектора линейно независимы, а значит, существует три инвариантные точки, причем эти точки различны и не лежат на одной прямой. Эти три точки образуют три неподвижные прямые.

• 3 случай. λ₁ = λ₂ ≠ λ₃ – действительные корни.

Пусть r = rang (М – λ₁∙Е), тогда число линейно независимых векторов в подпространстве решений равно 3 – r .

а) λ₁ = λ₂ - дают один линейно независимый вектор (r = 2). Тогда будет одна инвариантная точка при λ₁ и λ₃ – даст вторую инвариантную точку. Таким образом, всего две неподвижные точки, которые образуют неподвижную прямую.

б) λ₁ = λ₂ - дают два линейно независимых вектора, которые образуют двумерное подпространство решений (r = 1), которое в свою очередь порождает точечно неподвижную прямую. λ₃ – дает инвариантную точку не принадлежащую точечно неподвижной прямой.

• 4 случай. λ₁ = λ₂ = λ₃ – действительные корни.

а) r = 1 один линейно независимый вектор, а значит одна инвариантная точка;

б) r = 2 два линейно независимых вектора, а значит две инвариантные точки, которые определяют точечно неподвижную прямую;

в) r = 3 - не может быть (почему?).

Собственные вектора находятся из решения системы: (М – λ∙Е)·Х = О

Для нахождения инвариантных прямых характеристическое уравнение будет - det | λ ∙Е – М | = 0, а значит собственные значения те же самые. Собственные вектора находятся из решения системы: и∙(М – λ∙Е) = о.

Задача. Найти инвариантные точки коллинеаций:

а) Уравнение коллинеации

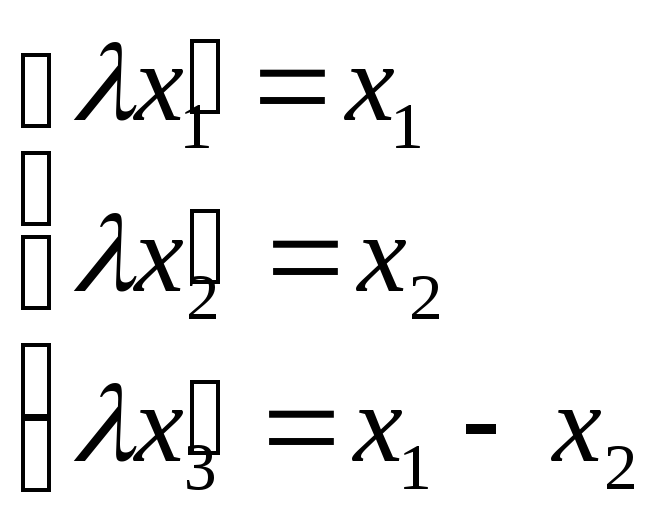
Решение. Матрица коллинеации .

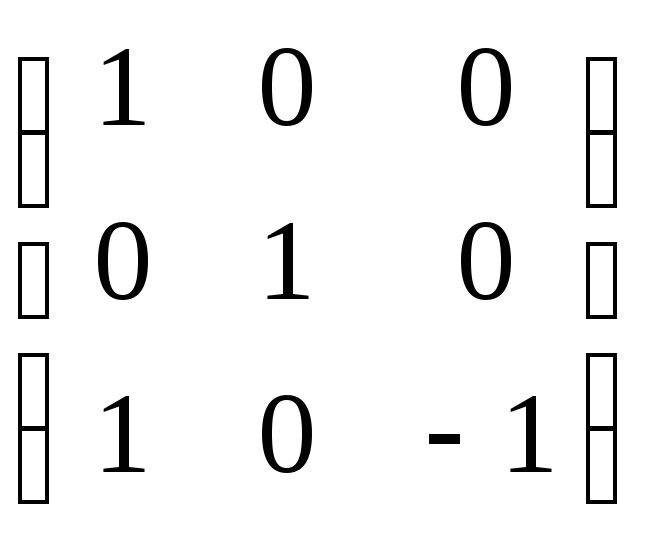Характеристическое уравнение: = 0

( 1 - λ)² ∙(- 1 – λ) = 0, λ₁ = λ₂ = 1, λ₃ = - 1.

При λ₁ = 1 ∙=

х₁ = 2∙х₃ , М₁ = и М₂ =.

При λ₁ = 1, rang= 1 коллинеация имеет точечно неподвижную прямую, проходящую через точки М₁ и М₂ , это прямая - х₁ - 2∙х₃ = 0.

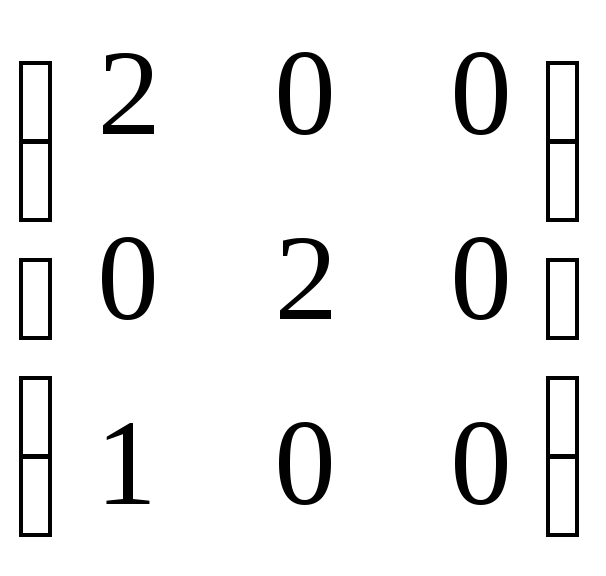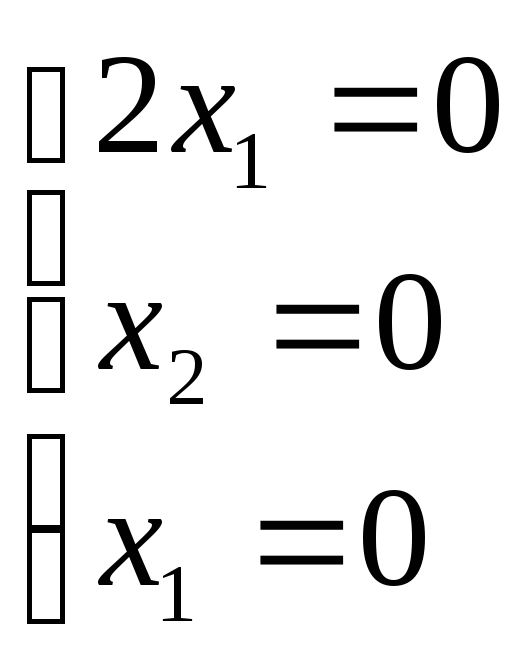
При λ₃ = -1 ∙= М₃=.

Кроме того инвариантными будут прямые проходящие через точку М₃ и любую точку прямой х₁ - 2∙х₃ = 0.

det |λ∙Е–М|=0 =0 λ₁ = λ₂ = 1, λ₃ = - 1.

При λ₁ = 1 (и₁ : и₂ : и₃ )∙=( 0 : 0 : 0 )

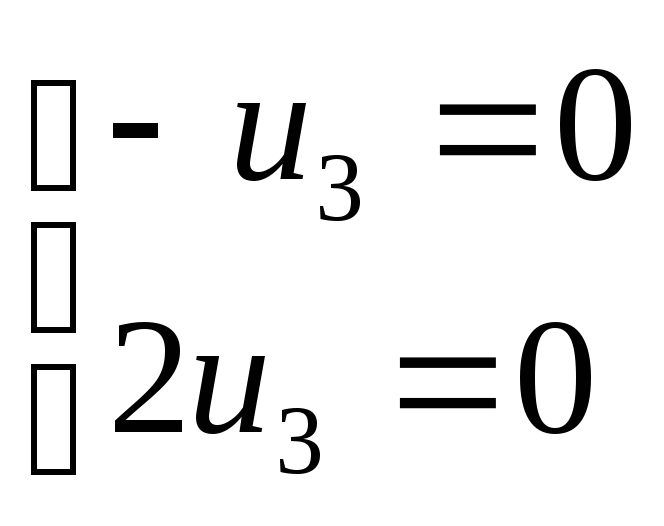
и ( 1 : 0 : 0 ) и v ( 0 : 1 : 0 ) имеем пучок инвариантных прямых (центр пучка - точка М₃): λ∙и + μ∙v

При λ₃ = - 1 ( и₁ : и₂ : и₃ )∙=(0 : 0 : 0 )

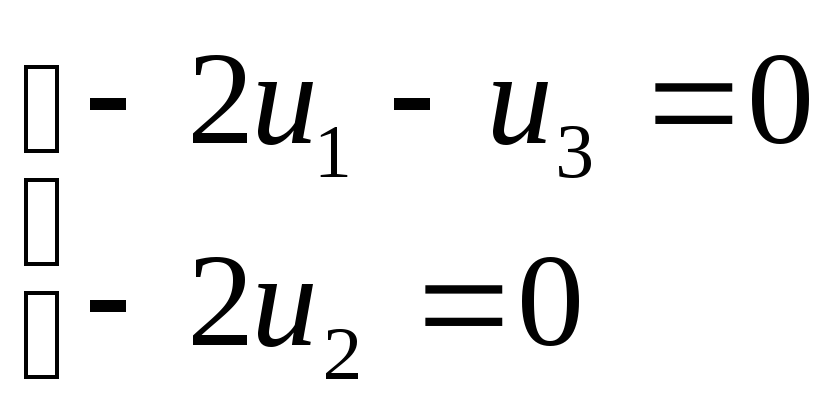
и ( 1 : 0 : -2 ) х₁ - 2∙х₃ = 0 - точечно неподвижная прямая..

б) Матрица коллинеации .

Решение.

Характеристическое уравнение 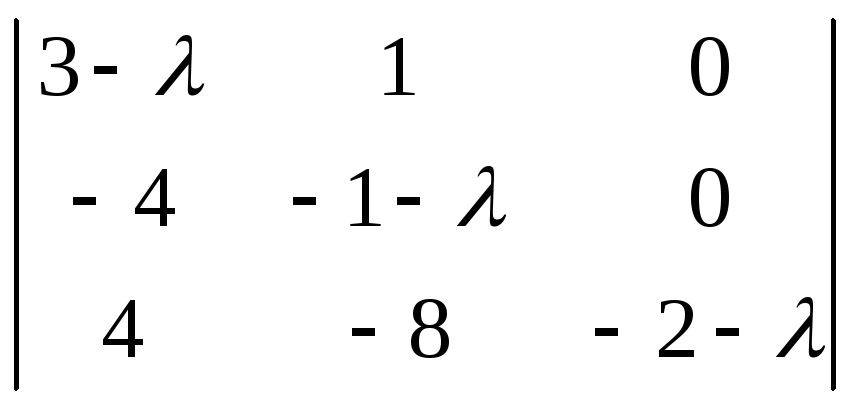=0

( λ² - 2λ + 1)∙(- 2 – λ) = 0, λ₁ = λ₂ = 1, λ₃ = - 2.

При λ₁= 1, ∙=

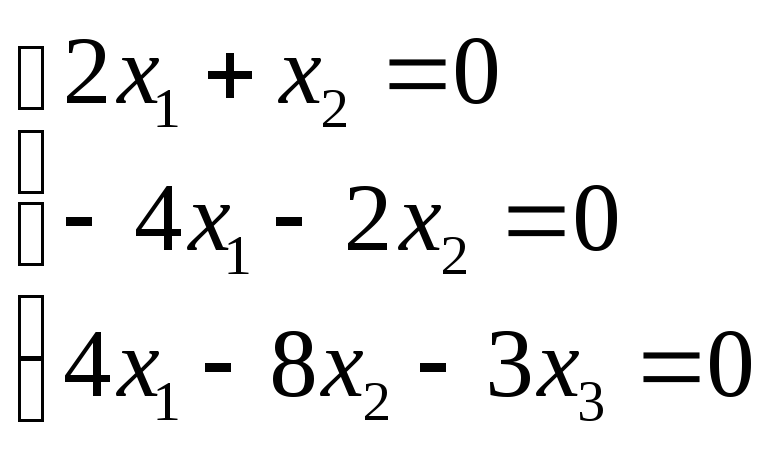
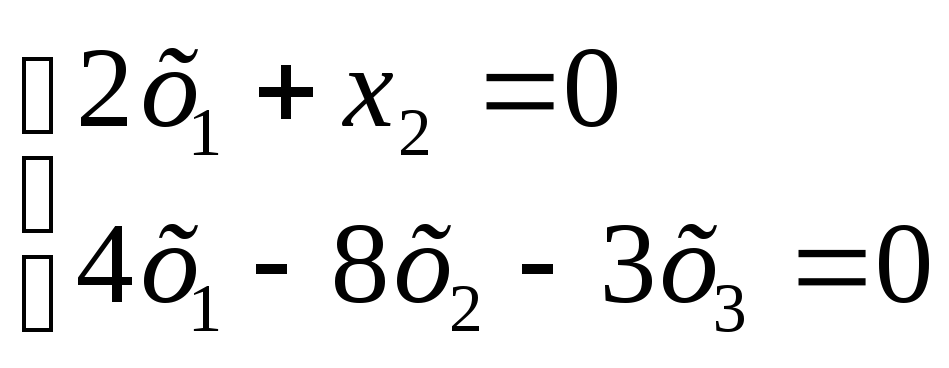
М₁ = .

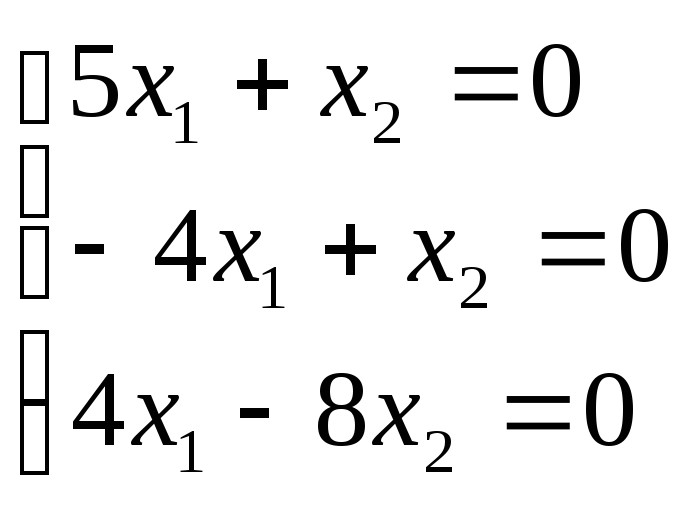
При λ₃ = - 2, ∙= М₃=.

Задача. Составить уравнение коллинеации, заданной четверками точек

А , В , С , D и А′ , В′ , С′ , D′ .

Решение. Формулы коллинеации имеют вид: λ∙Х ′=A∙Х.

Пусть матрица коллинеации А , тогда

λ₁∙А ′=A∙А → ,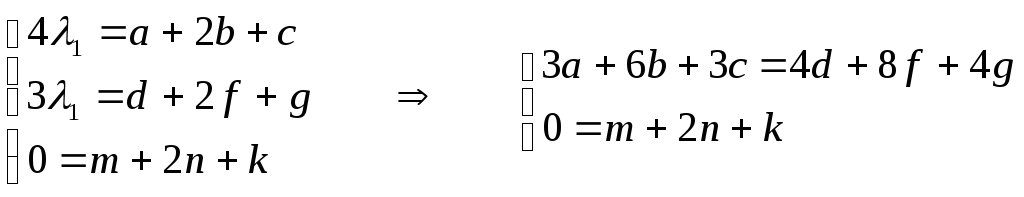

λ₂∙В ′=A∙В → ,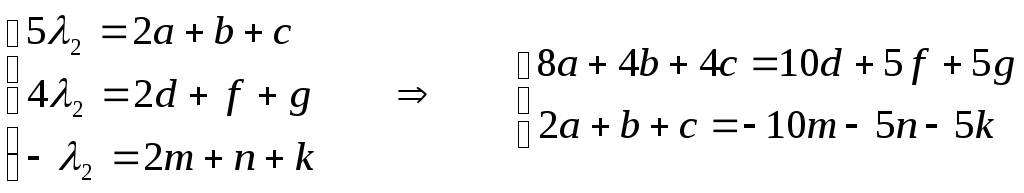

λ₃∙С′=A∙С → ,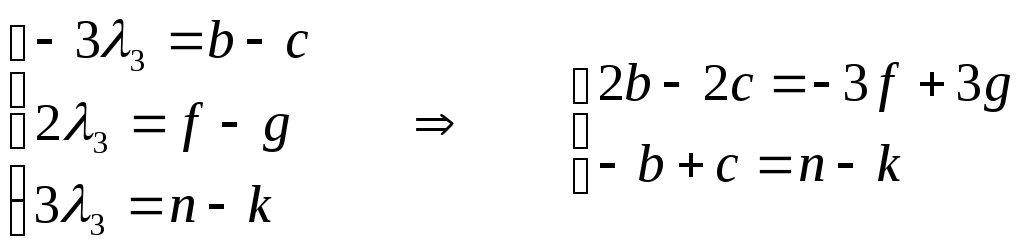

λ₄∙D ′=A∙D → .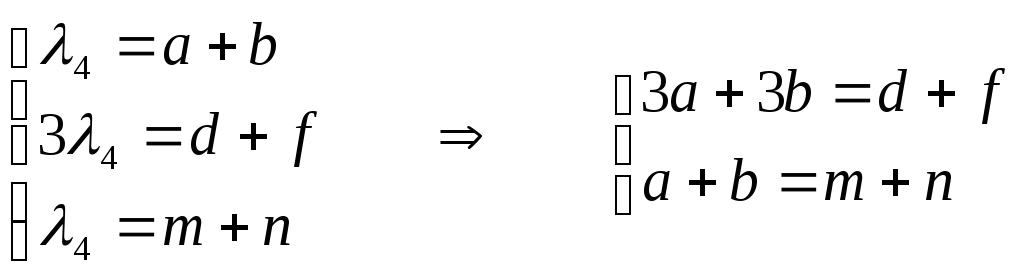

→ →

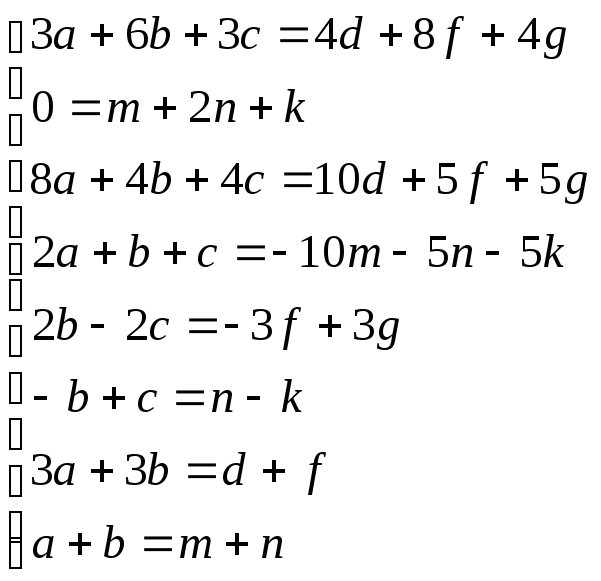Одно из решений: а=1, b=0, с=3, d=2, f=1, g= -1, т=0, п=1, k= -2,

тогда А .