
- •Аналитическое представление проективных преобразований 71
- •Дополнительная литература 91 введение
- •Структурно-логическая схема курса «проективная геометрия»
- •Исторические сведения
- •Проективное пространство
- •Аксиомы проективного пространства
- •Модели проективной прямой, проективной плоскости
- •Изоморфизм моделей
- •Проективная система координат
- •Проективный репер
- •Координаты точки на прямой (плоскости)
- •Принадлежность трёх точек одной прямой
- •Однородные проективные координаты
- •Уравнение прямой. Координаты прямой
- •Взаимное расположение двух прямых
- •Принадлежность трёх прямых одному пучку
- •Координаты точки и уравнение прямой в пространстве
- •Преобразование координат
- •Принцип двойственности
- •Теорема Дезарга
- •Простое отношение
- •Сложное отношение
- •Гармонизм
- •Гармонические свойства полного четырехвершинника
- •Квадрики на проективной плоскости
- •Классификация кривых второго порядка на проективной плоскости.
- •Взаимное расположение прямой и квадрики
- •Уравнение касательной
- •Полюс и поляра
- •Теорема Штейнера
- •Теорема Паскаля и ее предельные случаи
- •Задачи на построение, связанные с овалом
- •Прямые и квадрики на расширенной евклидовой плоскости
- •Проективные преобразования
- •Проективные преобразования плоскости
- •Аналитическое представление проективных преобразований
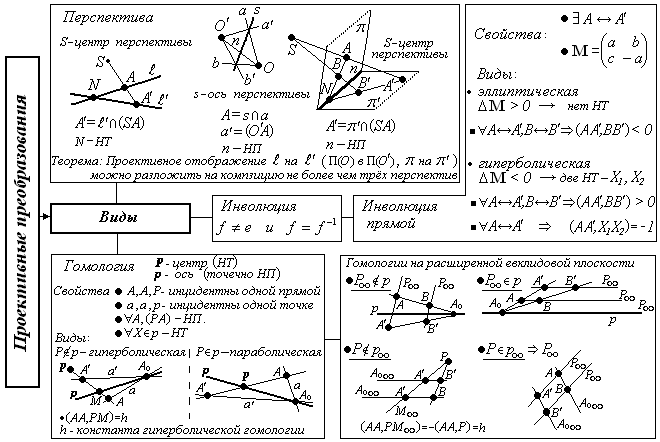
- •Перспектива
- •Отображение пучка в пучок
- •Инволюция
- •Коллинеация
- •Инварианты коллинеации
- •Гомология
- •Гомологии на расширенной плоскости
- •Дополнительная литература
Проективные преобразования
Проективные преобразования плоскости
Рассмотрим Р2 и реперы R(Е1,Е2,Е3,Е) и R′(Е′1,Е′2,Е′3,Е′).
Определение 1:
Отображение f
: Р2
→ Р2
заданное упорядоченной парой (R
, R′)
называется проективным
преобразованием,
если: ![]() М
М![]()
![]() Р2
→ f
(М)
=
Р2
→ f
(М)
=

![]() Р2
.
Р2
.
Замечание: Отображение f зависит только от реперов.
Замечание: Так как координаты точек и прямых определяются одинаково, то f (М) может быть как точкой, так и прямой.
Определение: Преобразование на проективной плоскости, переводящее точку в точку, а прямую в прямую называется коллинеация.
Определение: Преобразование на проективной плоскости, переводящее точку в прямую, а прямую в точку называется корреляция.
Замечание: Корреляция рассматривалась при обосновании принципа двойственности. В дальнейшем будем рассматривать коллинеации.
Лемма 1. При проективном преобразовании репер переходит в репер.
Доказательство. Пусть дано проективное преобразование плоскости
f : М![]() → М
′ = f
(М)
=
→ М
′ = f
(М)
=
 .
.
Тогда Е1
![]() → f
(Е1)=
→ f
(Е1)=![]() =
Е′1
, аналогично
отображаются
=
Е′1
, аналогично
отображаются
другие точки
репера: Е2![]() →
f (Е2)=
→
f (Е2)=![]() =Е′2
, Е3
=Е′2
, Е3![]() →
f (Е3)=
→
f (Е3)=![]() =Е′3
. □
=Е′3
. □
Свойства проективных преобразований:
1.
![]() А, В, С
А, В, С
![]() ℓ
ℓ
![]() А′, В′, С′
А′, В′, С′
![]() ℓ′.
ℓ′.
Доказательство.
Пусть в
репере R
уравнение
прямой (AB)
: и1·х1
+ и2·х2
+ и3·х3
=0 и
координаты точки С
 .
.
Так как А′ и В′ имеют те же самые координаты, что и точки А, В , но только в репере R′ , то уравнение прямой (А′В′) будет иметь такой же вид и1·х′1 + и2·х′2 + и3·х′3 =0 в R′.
Если точка С![]() (АВ),
то : и1·с1
+ и2·с2
+ и3·с3
=0.
(АВ),
то : и1·с1
+ и2·с2
+ и3·с3
=0.
Образ - С′

![]() и1·с1
+ и2·с2
+ и3·с3
=0 в R′,
а это означает что С′
и1·с1
+ и2·с2
+ и3·с3
=0 в R′,
а это означает что С′![]() (А′В′). □
(А′В′). □
Замечание: Для
корреляции:
![]() А, В, С
А, В, С
![]() ℓ
→
а′, b′, с′
ℓ
→
а′, b′, с′
![]() П(S).
П(S).
2.
![]() А, В, С
А, В, С
![]() ℓ
ℓ
![]() А′, В′, С′
А′, В′, С′
![]() ℓ′.
ℓ′.
Доказательство.
От противного:
![]() А, В, С
А, В, С![]() ℓ
и
А′, В′, С′
ℓ
и
А′, В′, С′
![]() ℓ′.
Возьмем
ℓ′.
Возьмем
![]() М
М![]() Р2
, пусть
(АВ)∩(СМ)
= N.
Р2
, пусть
(АВ)∩(СМ)
= N.
П ри
преобразовании А
→ А′, В → В′, С → С′, N → N′.
ри
преобразовании А
→ А′, В → В′, С → С′, N → N′.
А, В, N
![]() (АВ)
(АВ)
![]() А′, В′, N′
А′, В′, N′
![]() (А′В′),
С, М, N
(А′В′),
С, М, N
![]() (СМ)
(СМ)
![]()
С′, М′, N′
![]() (С′М′)
(по свойству (1)).
(С′М′)
(по свойству (1)).
По предположению
А′,В′,С′![]() ℓ′
ℓ′
![]() (А′В′)=ℓ′
(А′В′)=ℓ′
![]() N′
N′
![]() ℓ′
ℓ′
![]() (С′М′)=ℓ′.
(С′М′)=ℓ′.
Так как точка M – произвольная, получается, что вся плоскость отображается на прямую ℓ′. А это не возможно. □
Вывод: При проективном преобразовании сохраняется отношение инцидентности.
3. Сохраняется сложное отношение точек лежащих на одной прямой: (АВ,СD)=(А′В′,С′D′).
Доказательство. Так координаты точек образов и прообразов одинаковы, то при вычислении сложного отношения используются одни и те же числа, то сохраняется двойственное отношение.□
Определение
2: Отображение f
: Р2
→ Р2
заданное упорядоченной парой (R,R′)
называется проективным
преобразованием,
если:
![]() А, В, С, D
А, В, С, D
![]() ℓ
→
А′, В′, С′, D′
ℓ
→
А′, В′, С′, D′
![]() ℓ′
и (АВ,СD)=(А′В′,С′D′).
ℓ′
и (АВ,СD)=(А′В′,С′D′).
Замечание:
![]() а,
b, с, d
а,
b, с, d
![]() П(S)→
а′, b′, с′,
d′
П(S)→
а′, b′, с′,
d′![]() П(S′)
сохраняется (аb,сd)=(а′b′,с′d′).
П(S′)
сохраняется (аb,сd)=(а′b′,с′d′).
![]() А,
В, С, D
А,
В, С, D
![]() ℓ→
а′, b′, с′, d′
ℓ→
а′, b′, с′, d′
![]() П(f
(ℓ))
сохраняется (АВ,СD)=(а′b′,с′d′).
П(f
(ℓ))
сохраняется (АВ,СD)=(а′b′,с′d′).
Вывод: Корреляция как проективное преобразование попадает под это определение.
Теорема. Определения 1 и 2 эквивалентны.
Доказательство. Самостоятельно.
Лемма 2.
Пусть f1
:
Р2 →
Р2
и f2
:
Р2 →
Р2
- два
проективных преобразования, причем для
некоторой прямой ℓ
имеем, что А,В,С![]() ℓ
и f1(А)=f2(А),
f1(В)=f2(В),
f1(С)=f2(С),
тогда f1(ℓ)=f2(ℓ).
ℓ
и f1(А)=f2(А),
f1(В)=f2(В),
f1(С)=f2(С),
тогда f1(ℓ)=f2(ℓ).
(Если проективные преобразования f1 и f2 совпадают по трем точкам некоторой прямой, то они совпадают на всей прямой.)
Доказательство. От противного.
Возьмем
![]() М
М
![]() ℓ
и пусть f1
(М)≠f2
(М).
ℓ
и пусть f1
(М)≠f2
(М).
f1
- проективное
преобразование
![]() (АВ,СМ)=(f1(А)f1(В),f1(С)f1(М))=(А′В′,С′М1).
(АВ,СМ)=(f1(А)f1(В),f1(С)f1(М))=(А′В′,С′М1).
f2
- проективное
преобразование
![]() (АВ,СМ)=(f2(А)f2(В),f2(С)f2(М))=(А′В′,С′М2).
(АВ,СМ)=(f2(А)f2(В),f2(С)f2(М))=(А′В′,С′М2).
![]() (А′В′,С′М1)=(А′В′,С′М2),
но в силу единственности двойного
отношения следует М1=М2
для любой точки прямой ℓ
(А′В′,С′М1)=(А′В′,С′М2),
но в силу единственности двойного
отношения следует М1=М2
для любой точки прямой ℓ
![]() f1(ℓ)=f2(ℓ). □
f1(ℓ)=f2(ℓ). □
Теорема.
Пусть R(Е1
,Е2
,Е3
, Е)
и R′(Е′1
, Е′2
, Е′3
, Е′)
произвольные реперы на Р2.
Тогда существует единственное проективное
преобразование f
: Р2
→ Р2
, которое переводит репер в репер, причем
![]() М(
х1
: х2
: х3)R
→ f(М)=(
х1
: х2
: х3)R′
М(
х1
: х2
: х3)R
→ f(М)=(
х1
: х2
: х3)R′
Доказательство. Самостоятельно.
