Теорема Паскаля и ее предельные случаи

Определение: Шестивершинником называется совокупность шести различных упорядоченных точек А₁, А₂ , А₃ , А₄ , А₅ , А₆ , среди которых никакие три не лежат на одной прямой, и прямых (А₁А₂), (А₂А₃), (А₃А₄), (А₄А₅), (А₅ А₆), (А₆А₁). Точки называются вершинами, прямые называются сторонами.

Определение: Пары прямых:(А₁А₂) и (А₄А₅), (А₂А₃) и (А₅ А₆), (А₃А₄) и (А₆А₁) - называются противоположными сторонами.

Определение: Шестивершинник называется вписанным в овальную квадрику (или паскалевым), если его вершины принадлежат квадрике. Иногда говорят – шестивершинник, инцидентный квадрике.

Теорема Паскаля. Для того чтобы шестивершинник был инцидентен квадрике необходимо и достаточно, чтобы противоположные стороны шестивершинника пересекались в трех точках инцидентных одной прямой.

Замечание: Другая формулировка теоремы: для того чтобы шестивершинник был паскалевым необходимо и достаточно, чтобы противоположные стороны пересекались в коллинеарных точках.

А₁ , А₂ , А₃ , А₄ , А₅ , А₆ КВП P, Q, R – коллинеарны, где (А₁А₂)∩(А₄А₅)=P

(А₂А₃)∩(А₅А₆)=Q

(А₃А₄)∩(А₆А₁)=R

Доказательство. Пусть даны шесть точек А₁ , А₂ , А₃ , А₄ , А₅ , А₆ инцидентных квадрике, среди которых никакие три не коллинеарны.

Обозначим: (А₁А₂)∩(А₄А₅)=P,

(А₂А₃)∩(А₅А₆)=Q,

(А₃А₄)∩(А₆А₁)=R.

Через пять точек всегда проходит единственная квадрика.

Докажем, что принадлежность точки А₆ квадрике коллинеарности точек P, Q, R.

Рассмотрим репер R(А₁, А₂, А₃, А₄), пусть в этом репере точки А₅ и А₆ . Тогда уравнение квадрики: с₃∙(с₂ - с₁)∙х₁∙х₂ + с₂∙(с₁ - с₃)∙х₁∙х₃ + с₁∙(с₃ - с₂)∙х₂∙х₃=0 .

Точка А₆ КВП с₃∙(с₂ - с₁)∙d ₁ ∙d ₂ +с₂∙(с₁ - с₃)∙d ₁ ∙d ₃ +с₁∙(с₃ - с₂)∙d ₂ ∙d ₃ =0.

Найдем координаты точек P, Q, R в репере R(А₁, А₂, А₃, А₄).

Так как точки А₁, А₂, А₃ - базисные, то уравнения координатных

прямых будут: (А₁А₂) - х₃=0, (А₁А₃) - х₂=0, (А₂А₃) - х₁=0.

Уравнения прямых:

(А₃А₄) → =0 - х₁ + х₂ = 0,

(А₄А₅) → 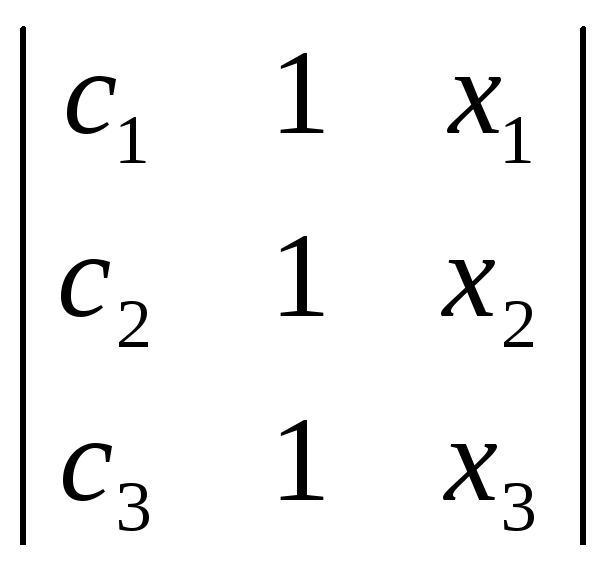=0 (с₂–с₃)∙х₁+(с₃–с₁)∙х₂+(с₁- с₂)∙х₃=0,

(А₅А₆) → =0

(с₂∙d₃ – с₃∙d₂)∙х₁ + (с₃∙d₁ – с₁∙d₃)∙х₂ + (с₁∙d₂ - с₂∙d₁)∙х₃ = 0,

(А₆А₁) → =0 - d₃∙х₂ + d₂∙х₃ = 0,

Р=(А₁А₂) ∩ (А₄А₅) →

Q=(А₂А₃) ∩ (А₅А₆) →

R=(А₃А₄) ∩ (А₆А₁) → .

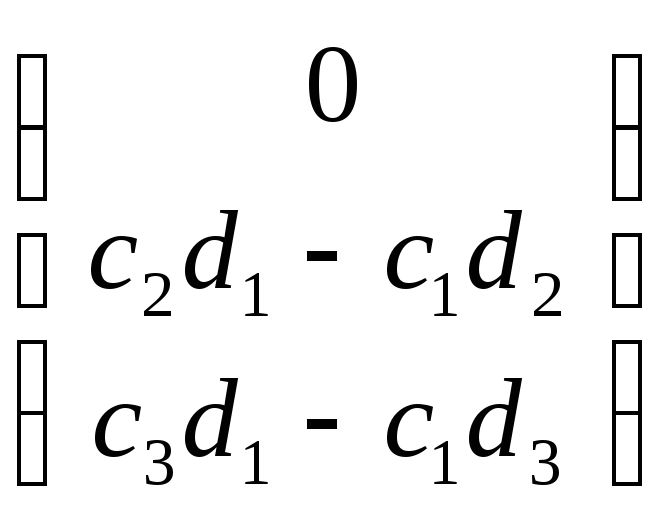Тогда координаты точек P , Q , R .

Запишем условие коллинеарности точек: 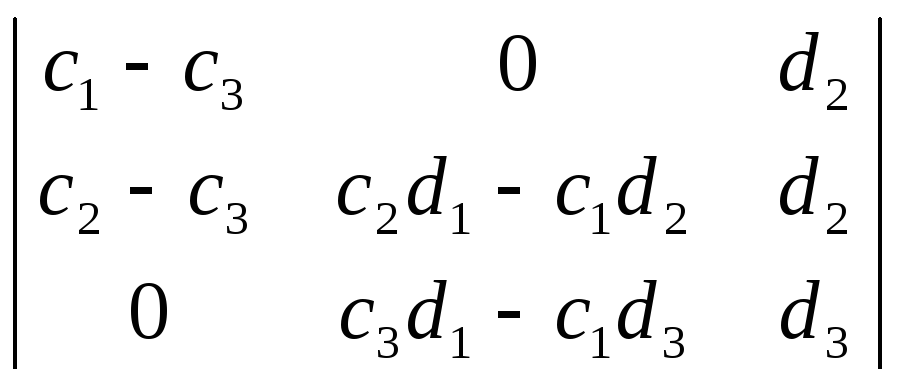=0

d₂∙(с₂-с₃)∙(с₃ d₁-с₁ d₃)-d₂∙(с₁-с₃)∙(с₃ d₁-с₁ d₃)+d₃∙(с₁-с₃)∙(с₂ d₁-с₁ d₂)=

=d₂∙(с₃ d₁ - с₁ d₃)∙(с₂ - с₃ - с₁ + с₃) + d₃∙(с₁ - с₃)∙(с₂ d₁ - с₁ d₂) = d₂∙(с₃ d₁-с₁ d₃)∙(с₂- с₁)+d₃∙(с₁-с₃)∙(с₂ d₁ -с₁ d₂)=

d₂∙с₃ d₁∙с₂ - d₂∙с₁ d₃∙с₂ – d₂∙с₃ d₁∙с₁ + d₂∙с₁ d₃∙с₁ + d₃∙с₁∙с₂ d₁ – d₃∙с₃∙с₂ d₁ - d₃∙с₁∙с₁d₂ + d₃∙с₃∙с₁ d₂ =

= d₂∙d₁∙(с₃∙с₂ - с₃∙с₁) - d₂∙d₃∙(с₁∙с₂ - с₃∙с₁) + d₃∙d₁ ∙(с₁∙с₂ - с₃∙с₂) =

= d₂∙d₁∙с₃∙(с₂ -с₁) + d₂∙d₃∙с₁∙(-с₂+с₃)+d₃∙d₁∙с₂∙(с₁ - с₃) =0 .

Т.о. условие коллинеарности точек P,Q,R условию А₆ КВП. □

Замечание: Частным случаем теоремы Паскаля является теорема Паппа.

Предельные случаи теоремы Паскаля

Рассмотрим овальную квадрику и инцидентный ей шестивершинник А₁ , А₂ , А₃ , А₄ , А₅ , А₆ .

Фиксируем вершину А₁, а вершину А₂ будем перемещать по квадрике так, чтобы она приближалась к точке А₁ , тогда прямая (А₁А₂) будет стремиться к предельному положению - касательной в точке А₁ . Такую фигуру будем называть предельным шестивершинником, он состоит из пяти точек и шести прямых, причем одна точка будет двойная - А₁₂, а прямая (А₁А₂) – касательной.

Аналогичным образом могут совпадать вершины какие-либо другие вершины. Например: А₃ = А₄ и/или А₅ =А₆ .

Замечание: Возможны случаи: А₂ = А₃ , А₄ = А₅ , А₆ = А₁ , но не возможно: А₂ = А₄ или А₂ = А₆ , также невозможен случай А₁ = А₂ = А₃ , т.е. совпадать могут только две вершины лежащие на одной стороне.

Определение: Фигура, двойственная шестивершиннику – шестисторонник а₁ а₂ а₃ а₄ а₅ а₆ .

а₁∩а₂=В₁, а₂∩а₃=В₂, а₃∩а₄=В₃ , а₄∩а₅=В₄ , а₅ ∩а₆=В₅ , а₆ ∩а₁=В₆.

Пары вершин - В₁ и В₄ , В₂ и В₅ , В₃ и В₆ называются противоположными.

Шестисторонник также как и шестивершинник состоит из шести прямых, среди которых никакие три не принадлежат одному пучку, и шести точек. Шестисторонник инцидентный квадрике будет уже не вписанным, а описанным вокруг квадрики.

Теорема двойственная теореме Паскаля носит название теорема Брианшона.

Теорема Брианшона. Для того чтобы шестисторонник касался овальной квадрики необходимо и достаточно, чтобы прямые, соединяющие противоположные вершины шестисторонника пересекались в одной точке (были инцидентны одной точке).

Замечание: Для этой теоремы тоже существует предельные случаи (рассмотреть самостоятельно.)