
- •Аналитическое представление проективных преобразований 71
- •Дополнительная литература 91 введение
- •Структурно-логическая схема курса «проективная геометрия»
- •Исторические сведения
- •Проективное пространство
- •Аксиомы проективного пространства
- •Модели проективной прямой, проективной плоскости
- •Изоморфизм моделей
- •Проективная система координат
- •Проективный репер
- •Координаты точки на прямой (плоскости)
- •Принадлежность трёх точек одной прямой
- •Однородные проективные координаты
- •Уравнение прямой. Координаты прямой
- •Взаимное расположение двух прямых
- •Принадлежность трёх прямых одному пучку
- •Координаты точки и уравнение прямой в пространстве
- •Преобразование координат
- •Принцип двойственности
- •Теорема Дезарга
- •Простое отношение
- •Сложное отношение
- •Гармонизм
- •Гармонические свойства полного четырехвершинника
- •Квадрики на проективной плоскости
- •Классификация кривых второго порядка на проективной плоскости.
- •Взаимное расположение прямой и квадрики
- •Уравнение касательной
- •Полюс и поляра
- •Теорема Штейнера
- •Теорема Паскаля и ее предельные случаи
- •Задачи на построение, связанные с овалом
- •Прямые и квадрики на расширенной евклидовой плоскости
- •Проективные преобразования
- •Проективные преобразования плоскости
- •Аналитическое представление проективных преобразований
- •Перспектива
- •Отображение пучка в пучок
- •Инволюция
- •Коллинеация
- •Инварианты коллинеации
- •Гомология
- •Гомологии на расширенной плоскости
- •Дополнительная литература
Взаимное расположение прямой и квадрики
Пусть дана овальная квадрика Х Т∙Q∙Х =0 и прямая (АВ).
Взаимное расположение
прямой и квадрики будет зависеть от
решения системы:
Если существует решение, тогда квадрика и прямая пересекаются.
Если решения не существует, тогда квадрика и прямая не пересекаются.
Параметрическое уравнение прямой подставим в уравнение квадрики.
(λ∙А
Т+
μ∙В
Т)∙Q∙(λ∙А
+ μ∙В)
=0
![]() λ²∙А
Т∙Q∙А
+ λ∙μ∙А
Т∙Q∙В+
μ∙λ∙В
Т∙Q∙А
+ μ²∙В
Т∙Q∙В
= 0
λ²∙А
Т∙Q∙А
+ λ∙μ∙А
Т∙Q∙В+
μ∙λ∙В
Т∙Q∙А
+ μ²∙В
Т∙Q∙В
= 0
Каждое из выражений А Т∙Q∙А , А Т∙Q∙В , В Т∙Q∙А , В Т∙Q∙В является числом,
так как матрицы Q , А , А Т, В , В Т - заданы.
(АТ∙Q∙В)Т = ВТ∙QТ∙АТТ=ВТ∙Q∙А, но АТ∙Q∙В - это число, а значит (АТ∙Q∙В)Т=АТ∙Q∙В, т.е. АТ∙Q∙В=ВТ∙Q∙А.
Обозначим АТ∙Q∙А = а, ВТ∙Q∙В= b, АТ∙Q∙В = ВТ∙Q∙А = с,
Тогда получим: λ²∙а + 2∙λ∙μ∙с + μ²∙b = 0 - однородное уравнение, разделим на μ² (параметры уравнения прямой λ и μ одновременно не обращаются в 0, хотя бы один их них отличен от 0).
![]() - квадратное
уравнение относительно
- квадратное
уравнение относительно
![]() .
.
D =4∙с² - 4∙а∙b = 4∙(АТ∙QТ∙В) ² - 4∙( АТ∙Q∙А)∙( В Т∙Q∙В).
Как известно, квадратное уравнение может иметь два, или один, или ни одного корня в зависимости от дискриминанта.
При D > 0, две точки пересечения, т.е. прямая будет секущей;
при D = 0, одна точка пересечения, т.е. прямая будет касательной к квадрике;
при D < 0, точек пересечения прямой и квадрики нет.
Замечание:
Аналогично можно рассматривать систему
 .
Выражая одну из переменных через две
другие и подставляя в уравнение квадрики,
получим однородное уравнение второй
степени от двух переменных. Решая
аналогичным способом, итоговый результат
будет тем же.
.
Выражая одну из переменных через две
другие и подставляя в уравнение квадрики,
получим однородное уравнение второй
степени от двух переменных. Решая
аналогичным способом, итоговый результат
будет тем же.

Вывод: Прямая может не иметь общих точек с квадрикой, может касаться её или быть секущей. Других вариантов нет.
Задача.
Установить взаимное расположение
квадрики х1²+х2²
-х3²-2∙х1∙х2
-4∙х1∙х3=0
и прямой, проходящей через точки А![]() и В
и В![]() .
.
Решение.
Первый способ: Q= -
матрица квадрики, тогда
-
матрица квадрики, тогда
а =АТ∙Q∙А
=
![]() ∙
∙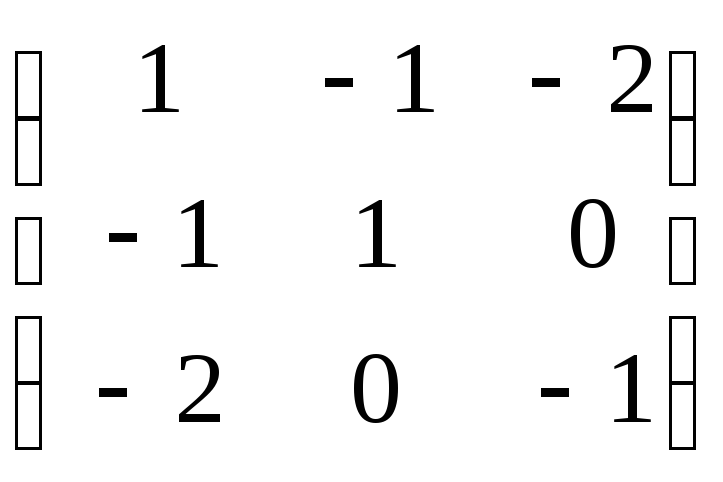 ∙
∙![]() =
12
=
12
b= ВТ∙Q∙В=![]() ∙
∙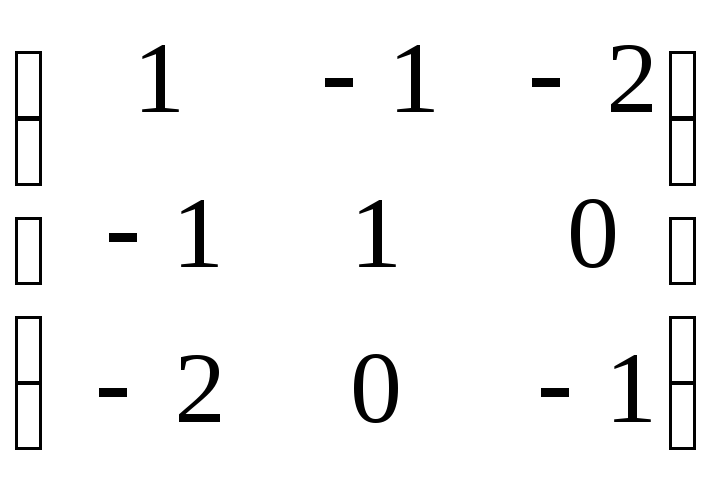 ∙
∙![]() =
4
=
4
с =
А Т∙Q∙В
=
![]() ∙
∙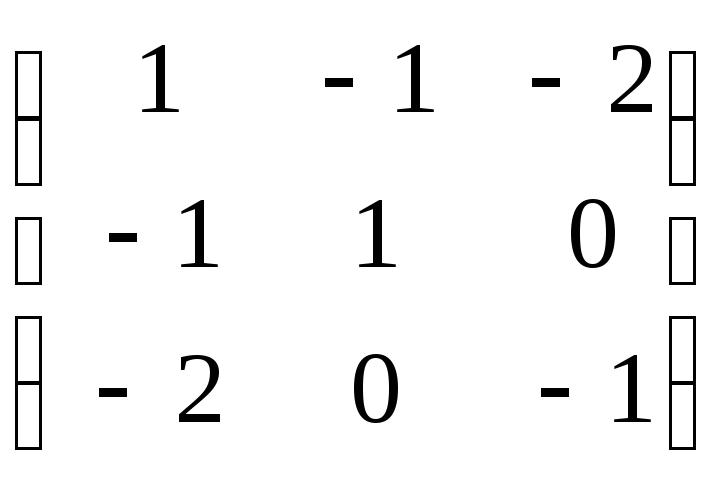 ∙
∙![]() =
-8,
=
-8,
![]()
![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
Одно решение λ1=1
и μ1=
3
![]() Х1
= 1∙
Х1
= 1∙![]() +
3 ∙
+
3 ∙![]() =
=![]() =
=![]() .
.
Второе решение
λ2=1
и μ2=1
![]() Х2
= 1∙
Х2
= 1∙![]() +
1 ∙
+
1 ∙![]() =
=![]() =
=![]() .
.
Прямая пересекает квадрику в двух точках Х1 и Х2.
Второй способ: Найдем уравнение прямой (АВ):
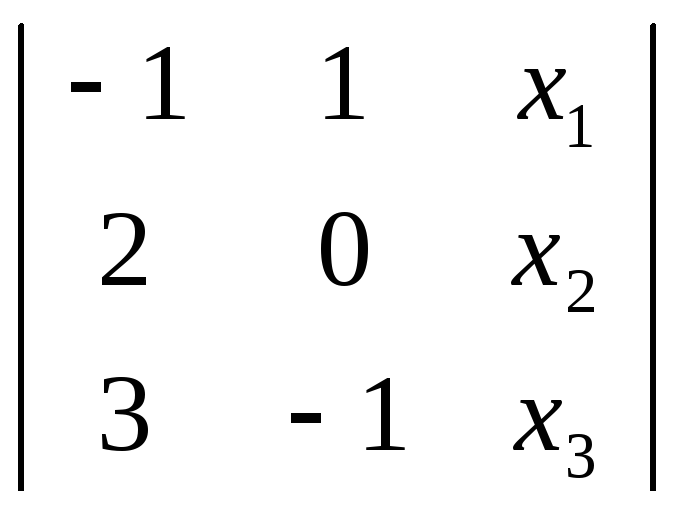 =0
=0
![]() - 2х1
+2х2
-2х3
= 0
- 2х1
+2х2
-2х3
= 0
![]() х1
- х2
+ х3
= 0.
х1
- х2
+ х3
= 0.
Решим систему
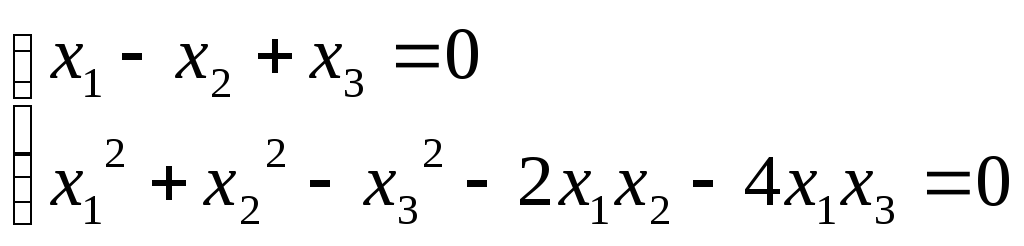
![]()

![]()
![]()
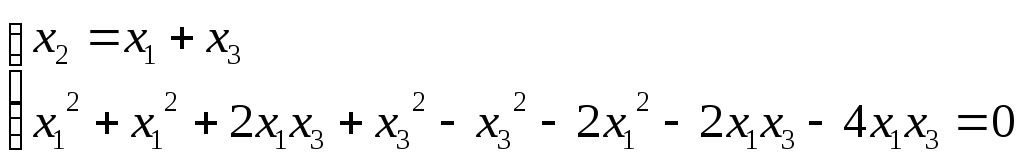
![]()
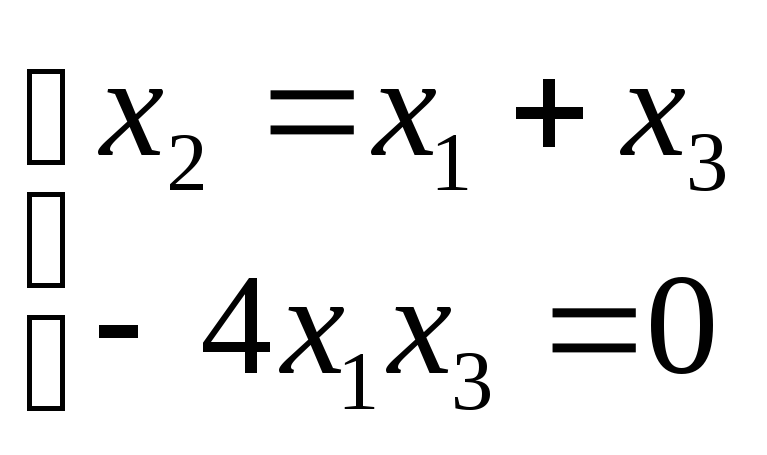
![]()
![]()
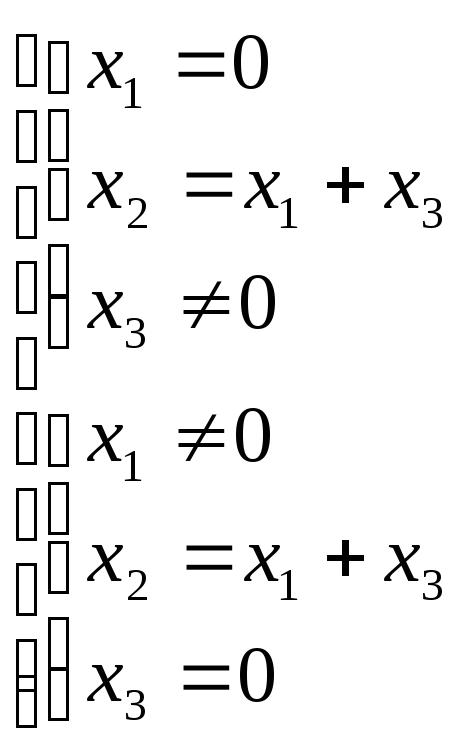
![]()

![]()
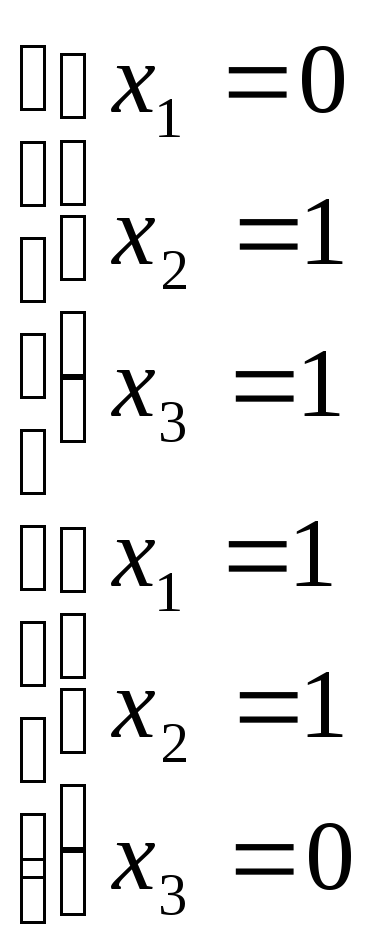
![]() Х1=
Х1=![]() и Х2=
и Х2=![]() -
точки пересечения (АВ) и КВП
-
точки пересечения (АВ) и КВП
Уравнение касательной
Рассмотрим случай касательной к овальной квадрике, (D = 0).
4∙(АТ∙QТ∙В)²-4∙(АТ∙Q∙А)∙(ВТ∙Q∙В)=0 ![]() (АТ∙QТ∙В)²-(АТ∙Q∙А)∙(ВТ∙Q∙В)=0.
(АТ∙QТ∙В)²-(АТ∙Q∙А)∙(ВТ∙Q∙В)=0.
Если точку А фиксировать, а точку В сделать переменной тогда уравнение касательной к квадрике, проведенной из точки А, будет следующим: (АТ∙QТ∙Х) ² - ( АТ∙Q∙А)∙( Х Т∙Q∙Х) = 0 (**)
Фактически это уравнение является квадратичной формой и в то же время уравнением прямой, то есть распадается на прямые. Проанализируем это уравнение для случая, когда точка А принадлежит квадрике и не принадлежит квадрике.
-
А
 КВП
КВП  АТ∙Q∙А=0
АТ∙Q∙А=0 (АТ∙QТ∙Х)²=0
- квадратичная форма (**) распалась на
две совпавшие прямые. Т.о. АТ∙QТ∙Х
=0 - уравнение касательной.
(АТ∙QТ∙Х)²=0
- квадратичная форма (**) распалась на
две совпавшие прямые. Т.о. АТ∙QТ∙Х
=0 - уравнение касательной. -
А
 КВП.
КВП.
(АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = 0 - ранг этой квадратичной формы не может равняться 3 потому, что это прямые, а значит квадратичная форма должна быть вырожденной. Так же ранг этой квадратичной формы не может быть равен 1. Докажем это от противного.
Пусть ранг (**) равен 1, тогда она распадается на две совпавшие прямые
(АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = (и∙Х)²
![]() ХТ∙Q∙Х=
ХТ∙Q∙Х=![]() ((АТ∙QТ∙Х)²
-(и∙Х)²)=
((АТ∙QТ∙Х)²
-(и∙Х)²)=![]() ((АТ∙QТ∙Х)-
и∙Х)
((АТ∙QТ∙Х)+и∙Х)
((АТ∙QТ∙Х)-
и∙Х)
((АТ∙QТ∙Х)+и∙Х)
![]() овальная
квадрика ХТ∙Q∙Х
распалась на линейные множители, на
прямые - это противоречие. Т.о. ранг (**)
равен 2, т.е. это или две пересекающиеся
прямые или две мнимые прямые пересекающиеся
в одной действительной точке.
овальная
квадрика ХТ∙Q∙Х
распалась на линейные множители, на
прямые - это противоречие. Т.о. ранг (**)
равен 2, т.е. это или две пересекающиеся
прямые или две мнимые прямые пересекающиеся
в одной действительной точке.
Вывод: Если точка принадлежит квадрике, то через неё можно провести только одну касательную. Если точка не принадлежит квадрике, то касательных или две или ни одной.
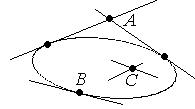
Определение: Точка называется внешней относительно квадрики, если через нее можно провести две касательных и внутренней, если касательных нет.
Лемма.
Пусть дана овальная квадрика х1²+х2²-х3²=0
и точка
![]() .
Точка является внутренней точкой
овальной квадрики тогда и только тогда,
когда а1²+а2²-а3²
< 0 (если а1²+а2²-а3²
> 0 - внешней).
.
Точка является внутренней точкой
овальной квадрики тогда и только тогда,
когда а1²+а2²-а3²
< 0 (если а1²+а2²-а3²
> 0 - внешней).
Доказательство. (Самостоятельно).
Задача. Дана квадрика 2∙х1²+х3²-2∙х1∙х2-2∙х1∙х3=0.
Найти уравнения
касательных к квадрике, проходящих
через точки А
![]() ,
В
,
В
![]() .
.
Решение.
Матрица квадрики Q= .
.
АТ∙Q∙А=(1:8:5)∙ ∙
∙![]() =(-11:-1:4)∙
=(-11:-1:4)∙![]() =1
=1![]() А
А
![]() КВП,
КВП,
Применим формулу (**) (АТ∙QТ∙Х)² - (АТ∙Q∙А)∙(Х Т∙Q∙Х) = 0.
АТ∙Q∙Х=(
1: 8 : 5 )∙ ∙
∙![]() =(-11
: -1 : 4)∙
=(-11
: -1 : 4)∙![]()
![]() 11∙х1+
х2 -
4∙х3=0
11∙х1+
х2 -
4∙х3=0
(11∙х1 + х2 - 4∙х3 )² - 1∙(2∙х1² + х3² - 2∙х1∙х2 - 2∙х1∙х3 ) =
= 121∙х1² + х2² + 16∙х3² + 22∙х1∙х2 - 88∙х1∙х3 - 8∙х2∙х3 - 2∙х1² - х3² + 2∙х1∙х2 + 2∙х1∙х3 =
= 119∙х1² + х2² + 15∙х3² + 24∙х1∙х2 - 86∙х1∙х3 - 8∙х2∙х3 =
= х2² +2∙х2∙12∙х1 -2∙х2∙4∙х3 +144∙х1² +16∙х3² -2∙12∙х1∙4∙х3 -144∙х1² -16∙х3² +96∙х1∙х3 +119∙х1² +15∙х3² -86∙х1∙х3 =
= (х2 + 12∙х1 -∙4∙х3 )² - 25∙х1² - х3² + 10∙х1∙х3 = (х2 + 12∙х1 -∙4∙х3 )² - (5∙х1 - х3 )² =
= ((х2 + 12∙х1 - 4∙х3 ) - (5∙х1 - х3 ))∙((х2 + 12∙х1 - 4∙х3 ) + (5∙х1 - х3 ))=
= (х2 + 12∙х1 - 4∙х3 - 5∙х1 + х3 )∙(х2 + 12∙х1 - 4∙х3 + 5∙х1 - х3 )=
= (х2 +7∙х1 -3∙х3 )∙(х2 +17∙х1 -5∙х3) = (7∙х1 + х2 - 3∙х3 )∙(17∙х1 + х2 - 5∙х3) = 0.
Т.о. касательные: 7∙х1 + х2 - 3∙х3 = 0 и 17∙х1 + х2 - 5∙х3 = 0.
ВТ∙Q∙В=(18:13:6)∙ ∙
∙![]() =
(17:-18:-12) ∙
=
(17:-18:-12) ∙![]() =0
=0
![]() В
В
![]() КВП.
КВП.
Уравнение касательной:
ВТ∙Q∙Х
= ( 18 : 13 : 6
)∙ ∙
∙![]() = 0
= 0 ![]() (
17 : -18 : -12 )∙
(
17 : -18 : -12 )∙![]() =
17∙х1
-18·х2
- 12∙х3
= 0.
=
17∙х1
-18·х2
- 12∙х3
= 0.
