
- •Аналитическое представление проективных преобразований 71
- •Дополнительная литература 91 введение
- •Структурно-логическая схема курса «проективная геометрия»
- •Исторические сведения
- •Проективное пространство
- •Аксиомы проективного пространства
- •Модели проективной прямой, проективной плоскости
- •Изоморфизм моделей
- •Проективная система координат
- •Проективный репер
- •Координаты точки на прямой (плоскости)
- •Принадлежность трёх точек одной прямой
- •Однородные проективные координаты
- •Уравнение прямой. Координаты прямой
- •Взаимное расположение двух прямых
- •Принадлежность трёх прямых одному пучку
- •Координаты точки и уравнение прямой в пространстве
- •Преобразование координат
- •Принцип двойственности
- •Теорема Дезарга
- •Простое отношение
- •Сложное отношение
- •Гармонизм
- •Гармонические свойства полного четырехвершинника
- •Квадрики на проективной плоскости
- •Классификация кривых второго порядка на проективной плоскости.
- •Взаимное расположение прямой и квадрики
- •Уравнение касательной
- •Полюс и поляра
- •Теорема Штейнера
- •Теорема Паскаля и ее предельные случаи
- •Задачи на построение, связанные с овалом
- •Прямые и квадрики на расширенной евклидовой плоскости
- •Проективные преобразования
- •Проективные преобразования плоскости
- •Аналитическое представление проективных преобразований
- •Перспектива
- •Отображение пучка в пучок
- •Инволюция
- •Коллинеация
- •Инварианты коллинеации
- •Гомология
- •Гомологии на расширенной плоскости
- •Дополнительная литература
Гармонизм
Определение: Если (AB,CD) = - 1, то четверка точек A,B,C,D называется гармонической.
Рассмотрим гармоническую четверку точек (AB,CD) = -1.
По свойству (2)
![]() (CD,
AB)
= (AB,CD)
= -1.
(CD,
AB)
= (AB,CD)
= -1.
По свойству (3)
![]() (AB,DC)
=
(AB,DC)
=
![]() = -1.
= -1.
Вывод: При перестановке пар и/или точек в паре гармонизм не нарушается.
Теорема. Четвёрка точек A, B,C, D∞ - гармоническая тогда и только тогда, когда точка C - середина AB . (третья точка – середина отрезка из первых двух).
Доказательство.
C –
середина AB
![]() (AB,C)
= 1.
(AB,C)
= 1.
![]() По свойству (6)
По свойству (6)
![]() (AB,CD∞)
= - (AB,C)
= - 1 - гармоническая четвёрка. В обратную
сторону докажите самостоятельно □
(AB,CD∞)
= - (AB,C)
= - 1 - гармоническая четвёрка. В обратную
сторону докажите самостоятельно □
Построение гармонических четвёрок.
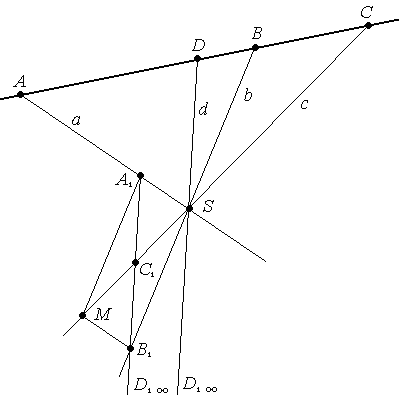
Задача 1. В пучке П(S) даны три прямые а, b, с. Построить прямую d такую, что (аb, сd) = -1.
Решение. Сложное отношение прямых пучка определяется сложным отношением точек пересечения этих прямых с какой-либо прямой не инцидентной пучку. Мы должны подобрать прямую таким образом, чтобы точки пересечения давали некоторый отрезок вместе с его серединой, тогда по теореме четвёртая гармоническая точка будет несобственной точкой. А значит, четвёртая гармоническая прямая в пучке будет параллельна подобранной прямой.
П остроение:
остроение:
1. На третьей прямой
с
выбираем
![]() М.
М.
2. Через неё проводим прямые параллельные а и b. (АМ)|| b и (ВМ)|| а
3. А=(АМ)∩а и В=(ВМ)∩b.
4. С=(АВ) ∩ с.
5. Четырехугольник АSВМ – параллелограмм, по свойству параллелограмма точка пересечения диагоналей является серединой диагонали. Т.е. С середина АВ. По теореме
четвертая гармоническая точка будет
несобственной, т.е. D∞ .
6. Искомая прямая - d=(SD∞).
Задача 2. В на прямой даны три точки A, B, C. Построить точку D такую, что (AB,CD) = -1.
Решение.
Будем использовать предыдущую
задачу Возьмем
![]() S'
S'
![]() (АВ).
(АВ).
Обозначим а=(АS'), b=(ВS), с=(СS'). Далее решение задачи 1.
Опишите последовательность построения самостоятельно.
Гармонические свойства полного четырехвершинника
Теорема. На каждой стороне полного четырехвершинника есть четвёрка гармонических точек, состоящая из двух вершин и двух точек пересечения этой стороны с диагональным трехвершинником.
Теорема. На каждой диагонали полного четырехвершинника есть четвёрка гармонических точек, состоящая из двух диагональных точек и двух точек пересечения этой диагонали со сторонами четырехвершинника.
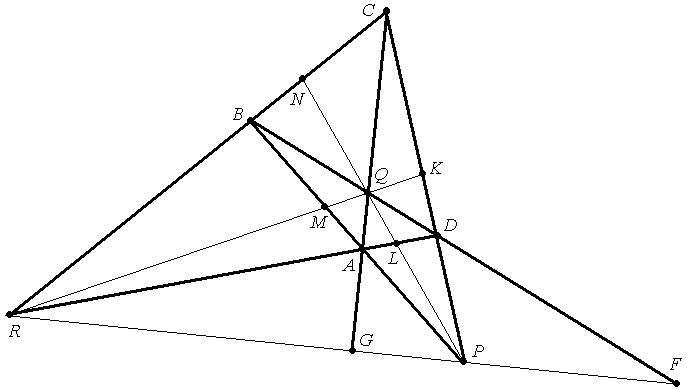
Гармоническими четверками будут на сторонах:
(AB,PM)=(АC,QG)=(AD,RL)=(BC,RN)=(BD,QF)=(CD,PK)= -1.
на диагоналях: (PQ,NL)=(PR,FG)=(RQ,MK)= -1.
Доказательство.
Рассмотрим репер R(
A,
B,
C,
D
). Тогда A![]() ,
B
,
B![]() ,
C
,
C![]() ,
D
,
D
![]() .
.
Точка Р
является проекцией единичной точки D
из третьей базисной точки С
на координатную прямую (АВ)
![]() Р
Р
![]() .
.
Точка Q
является проекцией единичной точки D
из второй базисной точки В
на координатную прямую (АС)
![]() Q
Q
![]() .
.
Точка R
является проекцией единичной точки D
из первой базисной точки А
на координатную прямую (ВС)
![]() R
R
![]() .
.
М
![]() (АВ)
(АВ) ![]() х3
= 0.
х3
= 0.
М
![]() (QR)
(QR)![]()
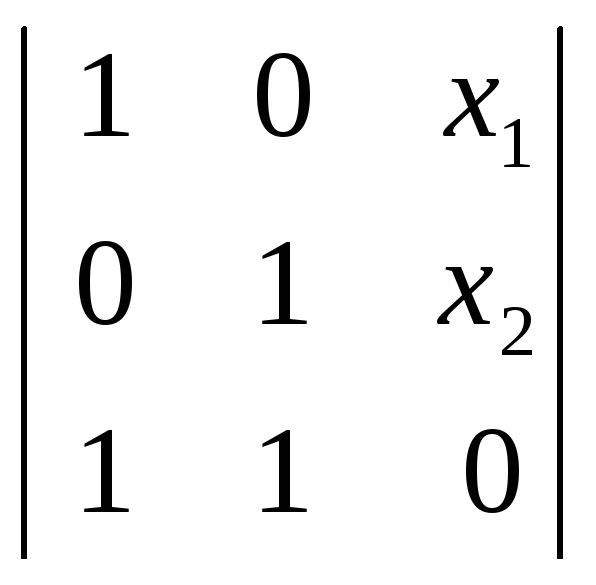 =0
=0![]() -
х1
– х2
= 0
-
х1
– х2
= 0![]() -
х1
= х2
-
х1
= х2![]() М
М
![]() .
.
Точки A
![]() ,
B
,
B
![]() ,
Р
,
Р
![]() ,
М
,
М
![]() лежат на одной прямой и подсчет сложного
отношения дает (АВ,РМ)=
- 1.
лежат на одной прямой и подсчет сложного
отношения дает (АВ,РМ)=
- 1.
Гармонизм других четверок можно доказать аналогично. □
Другой способ доказательства для других четверок основан на свойстве (7) сложного отношения (самостоятельно).
Замечание: В силу принципа двойственности верна теорема для четырехсторонника. (сам-но).
Построение четвертой гармонической точки с использованием свойств полного 4-вершинника
Задача. На прямой даны три точки - A, B, C. Построить четвёртую гармоническую точку D.
Решение. Мы должны подобрать какой-либо четырёхвершинник для которого точки А, В будут вершинами, а точка С одной из диагональных точек. При этом четвертая гармоническая точка будет пересечением диагонали со стороной (АВ).

Построение:
1. Берем произвольную
точку Р
![]() (АВ).
(АВ).
2. Проводим прямые (АР) и (ВР).
3. Через точку C
проводим произвольную прямую с,
так что Р
![]() с.
с.
4. С1= (ВР) ∩ с, D1 = (АР) ∩ с, Q = (АС1)∩(ВD1 ).
5. В четырехвершиннике АВС1D1 точки Р , Q , С – диагональные. Тогда (РQ)∩(АВ)= D - искомая.
Замечание: Если C – середина AB, тогда D будет бесконечно удаленной точкой.
Рассмотрим частные случаи полного четырёхвершинника на расширенной евклидовой плоскости.
-
Одна из диагональных точек - несобственная.
Н апример,
точка R∞
апример,
точка R∞
![]() (АD)
|| (ВС)
(АD)
|| (ВС)
![]() АВСD
– трапеция.
АВСD
– трапеция.
(AD,LR∞)=
(BC,NR∞)
= - 1![]()
по свойству гармонических четвёрок
точка L -середина отрезка AD,
а точка N - середина отрезка BC.
Вывод: Прямая проходящая через точку пересечения продолжений боковых сторон и точку пересечения диагоналей трапеции делит основания трапеции пополам. (Теорема о четырёх точках трапеции).
-
Две диагональные точки несобственные.
Например, точки
Р∞
и R∞
![]() (АD)
|| (ВС)
и (АВ)
|| (СD)
(АD)
|| (ВС)
и (АВ)
|| (СD) ![]() АВСD
– параллелограмм.
АВСD
– параллелограмм.
Т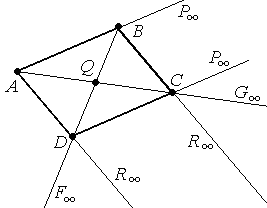 ак
как прямая (Р∞R∞)-
несобственная, то точки F,
G тоже
несобственные (АC,QG∞)=(BD,QF∞)=-1
ак
как прямая (Р∞R∞)-
несобственная, то точки F,
G тоже
несобственные (АC,QG∞)=(BD,QF∞)=-1![]()
точка Q - середина отрезков АС и BD.
Вывод: Точка пересечения диагоналей параллелограмма делит диагонали пополам.
(Свойство параллелограмма).
Задачи на построение.
Задача 1.
Даны прямые а
|| b, точки А,
В![]() а.
С помощью линейки построить середину
отрезка АВ.
а.
С помощью линейки построить середину
отрезка АВ.
Решение. Так прямые параллельны будем использовать частный случай четырехвершинника – трапецию.
Построение:
1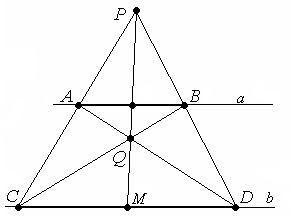 .
Берем
.
Берем
![]() Р
неинцидентную
прямым а и
b.
Р
неинцидентную
прямым а и
b.
2. Проводим прямые (АР) и (ВР).
3. Строим точки
С=(АР)∩b,
D=(ВР)∩b.
4. Q = (СВ)∩(АD).
5. (РQ)∩(АВ)= М - искомая середина отрезка.
Задача 2.
Даны точки А,
В, С![]() а
и точка D
а
и точка D![]() а ,
причем точка С
- середина отрезка АВ.
С помощью линейки, через точку
D провести
прямую b ||а.
а ,
причем точка С
- середина отрезка АВ.
С помощью линейки, через точку
D провести
прямую b ||а.
Решение. Так как необходимо построить параллельную прямую, будем использовать частный случай четырехвершинника – трапецию.
Построение:
1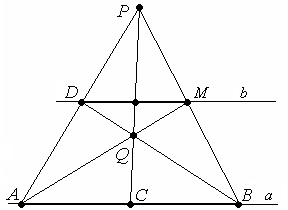 .
Проводим (АD).
.
Проводим (АD).
2. Берем
![]() Р
Р![]() (АD),
(АD),
Р≠А, Р≠D.
3. Проводим прямые (СР), (ВР) и (ВD).
4. Q = (СР)∩(ВD).
5. (АQ)∩(ВР)= М.
Искомая
прямая - (МD)||а.
Задача 3.
Даны прямые а
|| b, точки А,
В![]() а.
С помощью линейки удвоить отрезок АВ.
а.
С помощью линейки удвоить отрезок АВ.
Решение. Так прямые параллельны будем использовать частный случай четырехвершинника – трапецию.
Построение:
1. На прямой b возьмем две произвольные точки С и D.
2. Используя задачу 1, построим точку М – середину СD.
3. (АС)∩(ВМ)= Р.
4. (РD)∩а = N - искомая точка.

