
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач
§5. корені n-го степеня
У курсі алгебри розглядалось поняття квадратного кореня з невід’ємного числа. У даному параграфі узагальнимо це поняття, визначивши поняття кореня з довільним натуральним показником, більшим від 1.
1. Степеневі функції з натуральними показниками
Раніше ми розглядали функцію у = х2. Її аргумен- 
 том є основа степеня, значення функції при кожно-
том є основа степеня, значення функції при кожно-  му значенні аргументу є другим степенем аргумен-
му значенні аргументу є другим степенем аргумен-
ту. Таку функцію називають степеневою. Показник степеня у даному випадку дорівнює 2. Можна розглядати степеневі функції з показниками, відмінними від 2.
Степеневою функцією з натуральним показником |
будемо називати функцію у = хп, де п — натуральне |
число. |
Розглянемо спочатку степеневі функції з |
парними натуральними показниками, тобто |
функції виду у = х2, у = х4, у = х6, ... . Усі функції |
зазначеного виду мають ті самі властивості, що і |
функція у = х2, графік якої зображено на рис. 89. |
Вони визначені на множині дійсних чисел. Ці |
функції є парними. Наприклад, для функції |
у = х4 маємо: у(– х) = (– х)4 = х4 = у(х). Аналогічні |
обґрунтування можна навести для довільної |
зазначеної функції. Графіки цих функцій си- |
метричні відносно осі ординат. |
Степеневі функції з парними натуральними показниками на- |
бувають невід’ємних значень і мають лише один нуль: х = 0. Тому |
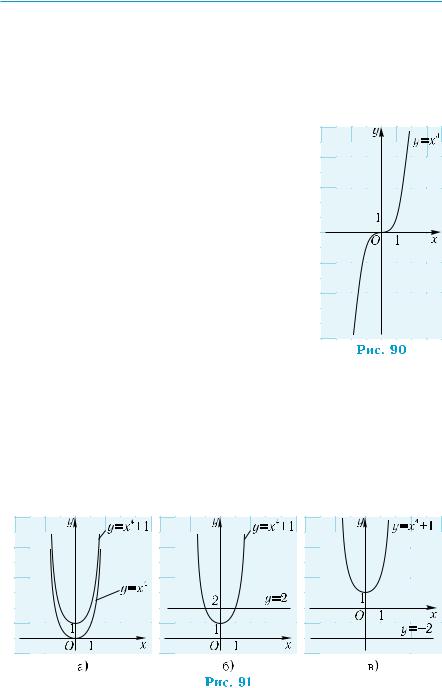
Корені п-го степеня |
83 |
їхні графіки лежать у верхній півплощині і проходять через поча- |
|
ток координат. Крім того, графіки усіх зазначених функцій про- |
|
ходять через точку з координатами (1; 1). |
|
Функції у = х2, у = х4, у = х6, ... зростають на проміжку [0; +∞) і |
|
спадають на проміжку (–∞; 0]. Їхні графіки схожі на графік, зо- |
|
бражений на рис. 89. |
|
Розглянемо тепер степеневі функції з не- |
|
парними натуральними показниками, відмін- |
|
ними від 1, тобто функції виду у = х3, у = х5, |
|
у = х7, … . Областю визначення цих функцій |
|
є множина дійсних чисел. Вони є непарними. |
|
Наприклад, для функції у = х5 маємо: у(– |
х) = |
= (–х)5 = – х5 = – у(х). Графіки цих функцій си- |
|
метричні відносно початку координат. |
|
Степеневі функції з непарними натураль- |
|
ними показниками є зростаючими. Вони ма- |
|
ють лише один нуль: х = 0. Їхні графіки прохо- |
|
дять через точку з координатами (1; 1) і схожі |
|
на графік, зображений на рис. 90. |
|
Зокрема, функцію у = х3 називають кубіч- |
|
ною, а її графік – кубічною параболою. |
|
Приклад 1. Графік функції f(x) = x4 + a проходить через точку
А(2; 17).
1)Знайти цю функцію, тобто число а.
2)Побудувати її графік.
3)Скільки коренів має рівняння f(x) = 2; f(x) = –2?
1) Оскільки графік функції проходить через точку А(2; 17), то координати цієї точки мають задовольняти рівняння f(x) = x4 + a,
6*

84 |
Розділ 1. Функції, їхні властивості та графіки |
тобто має справджуватись рівність 17 = 24 + а. Звідси одержимо а = 1. Отже, маємо функцію у = x4 + 1.
2) Графік функції у = x4 + 1 можна одержати із графіка функції у = x4 паралельним перенесенням його на 1 одиницю у додатному напрямі осі ординат (рис. 91, а).
3) Необхідно встановити, у скількох точках функція набуває значення 2. Перетнемо графік функції прямою у = 2. Графік перетинається у двох точках (рис. 91, б). Отже, рівняння x4 + 1 = 2 має два корені.
Рівняння x4 + 1 = –2 коренів не має, бо графік функції у = x4 + 1 не перетинається прямою у = –2 (рис. 91, в).
Багато залежностей між величинами описуються  за допомогою степеневих функцій з натуральними показниками.Наприклад,об’ємкубаV єстепеневою функцією від довжини його ребра а: V = а3; об’єм
за допомогою степеневих функцій з натуральними показниками.Наприклад,об’ємкубаV єстепеневою функцією від довжини його ребра а: V = а3; об’єм
кулі V є кубічною функцією її радіуса R: V (R) = 43 πR3 ; п’ятий член
геометричної прогресії є степеневою функцією від знаменника q: b5 = b1 q4.
!В останніх двох прикладах залежність має вигляд: y = axn, де х — аргумент, п — натуральне число, а — дея-
ке дійсне число. Такі функції зазвичай теж називають степеневими, як і функції виду y = a(x – b)n.
Розглянемо декілька задач на застосування степеневих функ- цій.
Приклад 2. Вкладник поклав на свій рахунок до банку 1000 грн. Банк нараховує щорічно за схемою складних відсотків р%. Знайти залежність розміру внеску через три роки S3 від р.
Згідно з формулою складних відсотків, маємо:
|
|
|
|
|
|
|
|
|
|
p |
3 |
|
|
|
S3 = |
1000 |
1 + |
|
|
. |
|||
|
|
|
100 |
||||||||
|
|
|
|
|
|
|
|
|
|
||
Ця залежність S3 від р є степеневою функцією. |
|||||||||||
|
|
|
|
|
p |
|
3 |
|
|
|
|
Відповідь. S3 |
= 1000 |
1 |
+ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
100 |
|
|
|
|
|||

Корені п-го степеня |
85 |
Приклад 3. Скільки коренів має рівняння |
|
х5 + х – 1 = 0? |
= |
Переписавши рівняння у вигляді х5 |
|
=1 – х, розв’яжемо задачу графічним методом. |
|
В одній системі координат побудуємо графіки |
|
функцій у = х5 і у =1 – х. Корені рівняння – |
|
це абсциси спільних точок графіків функцій. |
|
Графіки перетинаються в одній точці (рис. 92). |
|
Отже, рівняння має один корінь. |
|
Відповідь. Один. |
|
99 Контрольні запитання |
|
1°. |
Чи перетинає графік функції у = х6 |
пряма: |
|
ґ) у |
= –1? |
|
||||||||||||||
|
|
а) х |
= 0; |
|
б) х = 100; |
в) х |
= –1000; |
г) у = 10; |
|
|||||||||||
2°. |
Чи перетинає графік функції |
у = х5 |
пряма: |
|
ґ) у |
= –1? |
|
|||||||||||||
|
|
а) х |
= 0; |
|
б) х = 100; |
в) х |
= –1000; |
г) у = 10; |
|
|||||||||||
3. |
Які властивості функцій у |
= |
х4 і у = |
х5 |
є спільними? |
|
|
|
|
|
||||||||||
4. |
Скільки коренів має рівняння: |
= –7; |
г) х11 |
= 11? |
|
|
||||||||||||||
|
|
а) х4 = 2; |
|
|
б) х2 |
= –3; |
|
|
в) х5 |
|
|
|||||||||
5. |
Дано функції f(x) = x5 і g(x) = x10. Що більше: нуль чи число: |
|||||||||||||||||||
|
|
а) f(–5) |
f(–7); |
|
б) f(–10) – f(–20); |
в) g(–10) – g(–20)? |
|
|||||||||||||
6. |
Порівняйте числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
5 7 |
4 |
7 |
|
6 7 |
|
5 7 |
5 6 |
4 |
6 |
5 |
6 |
|
− |
4 |
6 |
||
|
|
а) |
і |
; |
б) |
|
і |
|
;в) |
|
і |
; г) |
|
і |
5 |
. |
||||
|
|
|
6 |
5 |
|
|
5 |
|
4 |
6 |
5 |
|
6 |
|
|
|
|
|||
|
|
|
|
|
2. Поняття кореня n-го степеня |
|
|
|
|
|
|
|||||||||
|
|
|
|
Як відомо, квадратним коренем з числа а назива- |
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
ють число, квадрат якого дорівнює |
а. Аналогічно |
|||||||||||||||
|
|
|
|
визначається поняття кореня довільного натураль- |
||||||||||||||||
|
ного степеня |
n з числа |
а. Це поняття необхідне для розв’язання |
|||||||||||||||||
багатьох задач, що зводяться до знаходження коренів рівняння хп = а. Наприклад, знаходження сторони куба х за його об’ємом V зводиться до розв’язання рівняння х3 = V.
Коренем n-го степеня (n N, n > 1) з числа а назива-
ється число, n-ий степінь якого дорівнює а.
86 |
Розділ 1. Функції, їхні властивості та графіки |
Так, коренем четвертого степеня з числа 256 є число 4, а також –4, бо 44 = (–4)4 = 256; коренем п’ятого степеня з числа 243 є число
3, оскільки 35 = 243.
Число 5 є коренем третього степеня з числа 125, оскільки 53 = 125, і коренем четвертого степеня з числа 625, бо 54 = 625.
Корінь третього степеня називають ще кубічним коренем. Мабуть, це пов’язано з тим, що об’єм V куба за його стороною х об- числюється за формулою V = х3. Довжина сторони куба є кубічним коренем з його об’єму.
Операцію знаходження кореня п-го степеня з числа а назива-
ють добуванням кореня п-го степеня з числа а. Корінь п-го степеня визначено лише для натуральних п ≥ 2.
!Зрозуміло, що кореня парного степеня з від’ємного чис- ла не існує, бо парний степінь будь-якого дійсного чис- ла є додатним числом.
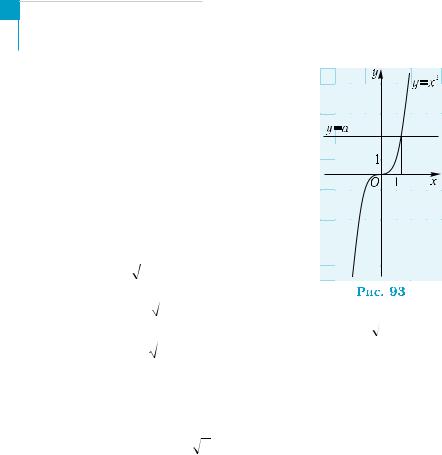
Розглянемо функцію у = х3. Будь-яка пряма |
|
|
||||
у = а |
перетинає графік цієї функції в єдиній |
|
|
|||
точці (рис. 93). А це означає, що для будь-якого |
|
|
||||
дійсного числа аіснує єдине значення х, третій |
|
|
||||
степінь якого дорівнює а. Інакше кажучи, для |
|
|
||||
будь-якого дійсного числа а існує єдине зна- |
|
|
||||
чення кореня третього степеня з цього числа. |
|
|
||||
Аналогічно можна дійти загального висно- |
|
|
||||
вку. Для довільного дійсного числа а і непар- |
|
|
||||
ного числа п існує єдине значення х, п-ий сте- |
|
|
||||
пінь якого дорівнює а. Це значення є коренем |
|
|
||||
п-го степеня з числа а. При непарному п його |
|
|
||||
позначають через |
n a |
(читають: корінь п-го |
|
|
||
степеня з числа а). |
3 −27 означає кубічний |
|
|
|||
Наприклад, |
запис |
|
|
|||
корінь з числа –27. З означення кореня випливає, що 3 −27 = −3 , |
||||||
бо (–3)3 = –27. Запис |
5 0,03125 означає корінь п’ятого степеня з |
|||||
числа |
0,03125. |
Його |
значення дорівнює 0,5, оскільки (0,5)5 |
= |
||
= 0,5 |
0,5 0,5 |
0,5 |
0,5 = 0,03125. |
справджується рів- |
||
За означенням, |
для довільного числа а |
|||||
ність: |
|
|
|
|
|
|
|
|
|
|
(2k+1 a )2k+1 = a. |
|
|

Корені п-го степеня |
87 |
Зауважимо, що при будь-якому натуральному значенні k число |
|
2k + 1 є непарним. |
|
Розглянемо тепер функцію у = х4. Будь- |
|
яка пряма у = а при a |
> 0 перетинає графік |
цієї функції у двох точках (рис. 94), тобто |
|
для будь-якого додатного числа а існують |
|
два значення х, четвертий степінь яких до- |
|
рівнює а. Інакше кажучи, для будь-якого до- |
|
датного числа а існують два значення коре- |
|
ня четвертого степеня з цього числа. |
|
Аналогічно можна дійти загального висновку. Для довільного |
|
a > 0 і парного числа п існують два протилежних числа, п-ий сте- |
|
пінь яких дорівнює а. При а = 0 таке число єдине, х = 0. При a < 0 |
|
таких чисел не існує. |
При парному п знаком n a позначають |
невід’ємний корінь п-го степеня з числа а. Від’ємний корінь п-го |
|
степеня із додатного числа а записується так: −n a. |
|
За означенням, для довільного невід’ємного числа а справ- |
|
джується рівність: |
(2k a )2k = a. |
|
|
Наприклад, запис 6 729 означає невід’ємний корінь шостого сте- |
|
пеня із 729. Маємо: 6 729 = 3, бо число 3 є невід’ємним і 36 = 729. |
|
Приклад 4. Обчислити: |
( 22)2 |
+ (3 −2 )3 |
|
|
|||||||||
|
|
|
|
2 |
5 32 |
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Згідно з означенням кореня п-го степеня, маємо: |
|
||||||||||||
|
( 22)2 + (3 −2 )3 |
= |
22 −2 |
= |
20 |
= 5. |
|
||||||
25 32 |
|
|
|
|
|
|
2 2 |
4 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Відповідь. 5. |
|
|
|
|
|
|
|
|
|
|
|||
|
Як відомо, для квадратного кореня знаком |
a по- |
|||||||||||
|
|||||||||||||
|
значався невід’ємний корінь з невід’ємного числа а. |
||||||||||||
|
Тому a2 = |
|
a |
|
: адже число |a| є невід’ємним і його |
||||||||
|
|
||||||||||||
|
квадрат дорівнює а2. |
|
|
|
|
||||||||
|
|
|
|
|
|||||||||
Так само при довільному парному показнику кореня, що дорівнює 2k, знаком 2k a ми позначили невід’ємний корінь 2k-го степеня з числа а. Тому 2k a2k = a .

88 |
Розділ 1. Функції, їхні властивості та графіки |
Справді, число |a| є невід’ємним і його 2k-ий степінь дорівнює а2k. У цій формулі не можна випускати знак модуля, інакше для від’ємних значень а одержимо неправильні результати. Так,
4 (−1)4 = 4 1 =1. Якщо ж скористатися зазначеною формулою і випус- титизнакмодуля,одержимопомилковийрезультат 4 (−1)4 = −1 .
Розглянемо тепер корені непарного степеня. При непарному |
|||||||
п= 2k |
+1єдинезначеннякореняздовільногочислаамипозначали |
||||||
через |
2k+1 a . Згідно з означенням, 3 53 = 5, 3 (−5)3 |
= −5, 3 a3 = a, |
|||||
5 a5 |
= a і т. д. для будь-якого числа а. Таким чином, для коренів |
||||||
непарного степеня справджується формула: |
|
|
|
||||
|
|
2k+1 a2k+1 = a . |
|
|
|
||
Наприклад, 3 ( 3 −2)3 = 3 −2 , але 4 ( 3 −2)4 = |
|
|
3 −2 |
|
= 2 − 3 , |
||
|
|
||||||
бо |
3 |
< 2. |
|
|
|
|
|
Приклад 5. Спростити вираз 6 x6 + 5 x5 . |
|
|
|
||||
Згідно з наведеними вище формулами, маємо: 6 x6 + 5 x5 =
=|x| + x. Якщо х ≥ 0, то |x| = x і |x| + x = x + x = 2x. Якщо ж х < 0, то
|x| = –x і |x| + x = –x + x = 0.
Відповідь. 2х, якщо х ≥ 0; 0, якщо х < 0.
Приклад 6. Побудувати графік функції |
y = 4 (x −2)4 . |
Оскільки 4 (x −2)4 = x −2 , то маємо |
функцію y = |x – 2|, графік якої можна одер |
жати із графіка функції y = |x| паралельним |
перенесенням останнього на 2 одиниці у |
додатному напрямі осі абсцис (рис. 95). |
99 Контрольні запитання
1°. Чи правильно, що число –3 є коренем четвертого степеня з числа 81?
2°. Чи правильно, що корінь четвертого степеня з числа 81 дорів- нює –3?
3°. Скільки існує коренів п’ятого степеня з числа –1024?

Корені п-го степеня |
89 |
|
4°. |
Скільки існує коренів четвертого степеня з числа 625? |
|
5°. |
Які з даних виразів не мають змісту: −16; 3 −27; |
6 (−2)2 ; |
6(−2)3 ; 5 (−2)3 (−3)2 ; 4 (−2)3 (−3)2 ?
6.Відомо, що об’єм V кулі обчислюється за формулою V = 43 πR3 , де R — радіус кулі. Кубічним коренем з якого числа є радіус кулі,
якщо V = 4,5?
7.Чому дорівнює: а) 4 74 ; б) 6 (−7)6 ; в) 5 (−7)5 ?
8*. Між якими двома послідовними цілими числами міститься число 3 15?
3. Арифметичний корінь n-го степеня та його властивості
 Вище зазначалось, якщо п — непарне число, то ви-
Вище зазначалось, якщо п — непарне число, то ви- 
 раз n a має зміст при будь-якому значенні а; якщо
раз n a має зміст при будь-якому значенні а; якщо
п— парне число, то вираз n a має зміст лише при
а≥ 0 і набуває тільки невід’ємного значення.
Вираз n a при а ≥ 0 має зміст як при парному п, так і при непар- ному п, і значення цього виразу є невід’ємним числом. Його назива- ютьарифметичнимкоренемп-гостепенязчислаа.Числоаназива-
ється підкореневим виразом, п — показником кореня.
Арифметичним коренем п-го степеня із невід’ємного числа а називають невід’ємне число, п-ий степінь якого дорівнює а.
Корінь непарного степеня із від’ємного числа можна виразити че- резарифметичнийкорінь.Наприклад, 3 −18 = −3 18 ,оскільки,згідно
з означенням, 3 −18 = −12 , −3 18 = −12 . Взагалі, при довільному до-
датному а і при непарному п справджується рівність n −a = −n a. Нам уже відомі властивості арифметичного квадратного коре-
ня. Аналогічні властивості має арифметичний корінь п-го степе- ня і при п ≥ 2.
В л а с т и в і с т ь 1. Якщо а ≥ 0 і b ≥ 0, то n ab = n a n b.
Арифметичний корінь п-го степеня з добутку двох невід’ємних чисел дорівнює добутку арифметичних коренів п-го степеня з цих чисел.
90 |
Розділ 1. Функції, їхні властивості та графіки |
В л а с т и в і с т ь 2. Якщо а ≥ 0 і b > 0, то n ab = nn ab .
Арифметичнийкоріньп-гостепеняздробу,чисельник якого невід’ємний, а знаменник додатний, дорівнює арифметичному кореню п-го степеня із чисельника, поділеному на арифметичний корінь п-го степеня зі знаменника.
Приклад 7. Обчислити: 1) 6 64 729; 2) 5 8 |
5 4; |
3) |
4 313 ; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
4) |
|
|
4 243 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1) Згідно з властивістю 1, 6 64 729 = 6 64 6 729 = 2 3 = 6. |
|
||||||||||||
|
|
|
2) Застосовуючи |
властивість |
1, |
матимемо: |
5 8 5 4 = 5 8 4 = |
|||||||||
= 5 32 = 2. |
|
|
|
|
|
|
13 |
|
256 |
|
||||||
|
|
|
3) Застосовуючи |
властивість |
2, |
одержимо |
4 3 |
= 4 |
= |
|||||||
|
|
4 256 |
|
|
4 =1 |
1 . |
|
|
|
|
|
81 |
|
81 |
|
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|||||
4 81 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
3 |
|
|
|
|
4 243 |
|
243 |
|
||||
|
|
|
4) Застосовуючи |
властивість |
2, |
матимемо: |
= 4 |
= |
||||||||
|
|
|
4 3 |
3 |
||||||||||||
= 4 81 = 3. |
|
|
|
|
|
|
||||||||||
|
|
|
Відповідь. 1) 6; 2) 2; 3) 11 ; 4) 3. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Приклад 8. |
Порівняти значення виразів 3 729 |
і 6 729. |
|
|||||||||||||
|
|
|
Застосовуючи |
означення |
кореня, послідовно |
матимемо: |
||||||||||
|
3 729 = |
9 = 3, 6 729 = 6 36 = 3. Ми бачимо, що значення цих ви- |
||||||||||||||
разів дорівнюють одне одному, тобто |
3 729 = 6 729. |
|
|
|
|
|||||||||||
|
|
|
Відповідь. |
3 729 = 6 729. |
|
|
|
|
|
|
|
|
||||
Аналізуючи останній приклад, можна висловити наступні при- пущення.
В л а с т и в і с т ь 3. Якщо а ≥ 0, то для натуральних n і k, більших від 1, справджується рівність n k a = nk a.

Корені п-го степеня |
91 |
В л а с т и в і с т ь 4. Якщо а ≥ 0, то для натуральних n, m і k, n > 1, справджується рівність nk amk = n am .
Властивість 4 іноді називають головною властивістю кореня. Її можна сформулювати так:
якщо показник кореня і показник степеня підкорене- вого виразу помножити або поділити на те саме нату- ральне число, то значення кореня не зміниться.
Наприклад, 8 34 = 3; 8 36 = 4 33 .
Властивості 1–4 дають змогу вносити множник під знак ариф- метичного кореня і виносити множник з-під знака кореня.
Наприклад, розкладаючи підкореневий вираз числа 4 48 на прості множники і застосовуючи означення кореня і властивість
1, можна винести множник з-під знака кореня: 4 48 = 4 24 3 = = 4 24 4 3 = 24 3. Виконуючи ці перетворення у зворотному поряд- ку, можна внести множник під знак кореня: 23 3 = 3 23 3 3 = = 3 23 3 = 3 24.
Приклад 9. Спростити вираз:
1) 3 54 + 4 48 −33 2 −34 3; 2) 27 4 9; 3) 4 33 3.
1) Виносячи множники з-під перших двох коренів, матимемо:
3 54 + 4 48 −33 2 −34 3 = 3 27 2 + 4 16 3 −33 2 −34 3 =
=3 27 3 2 + 4 16 4 3 −33 2 −34 3 = 33 2 + 24 3 −33 2 −34 3 = −4 3.
2)Скориставшись головною властивістю кореня і властивістю
1, одержимо: 27 4 9 = 27 4 32 = 27 3 = 27 3 = 81 = 9.
3) Внесемо множник 3 під знак арифметичного кореня третьо-
го степеня: |
4 33 3 = 4 3 33 3 3 = 4 3 34 . Згідно із властивістю 3, |
4 3 34 = 12 34 . |
Застосовуючи головну властивість кореня, дістане- |
мо: 12 34 = 3 3. |
Отже, 4 33 3 = 3 3. |
Відповідь. 1) −4 3;2) 9; 3) 3 3 .
Якщо потрібно перемножити або поділити корені з додатних чисел з однаковими показниками, то, згідно із властивостями 1 і 2, достатньо перемножити або поділити їхні підкореневі вирази і записати добуток або частку під знаком кореня з тим самим по- казником.
92 |
Розділ 1. Функції, їхні властивості та графіки |
!Якщо ж показники коренів, що перемножуються або діляться, різні, то необхідно їх привести до спіль- ного показника. Це робиться на підставі головної властивості кореня, тобто кожний показник кореня множиться на підібраний додатковий множник од- ночасно з піднесенням підкореневого виразу до того самого степеня. За спільний показник слід взяти най- менше спільне кратне показників коренів, що пере- множуються або діляться.
Приклад 10. Подати вираз у вигляді кореня з деякого числа: 1) 3 2 4 5; 2) 36 39 .
1) Оскільки множники є коренями різних степенів, то при- ведемо їх до спільного показника. Найменшим спільним кратним показників 3 і 4 є число 12. Показники коренів слід помножити на додаткові множники: 12 : 3 = 4, 12 : 4 = 3. Згідно з головною властивістю кореня, маємо:
3 2 4 5 = 3 4 24 4 3 53 = 12 24 12 53 .
Користуючись властивістю 1, перемножимо отримані корені з
однаковими показниками: 12 24 12 53 = 12 24 53 = 12 2000 .
2) Враховуючи те, що найменшим спільним кратним показни-
ків коренів, тобто чисел 3 і 6, є число 6, то, згідно із головною влас- тивістю кореня, матимемо:
|
3 9 |
= |
6 92 |
|
= 6 |
92 |
= 6 |
27 = 6 33 |
= |
3. |
6 3 |
6 3 |
|
3 |
|||||||
|
|
|
|
|
|
|
||||
Відповідь. 1) 12 2000 |
; 2) |
3 . |
|
|
|
|||||
 Використовувати властивості 1–4 при перетворенні
Використовувати властивості 1–4 при перетворенні  виразів з коренями слід дуже обережно, обов’язково перевіряючи виконання умов, за яких вони справ- джуються. У супротивному випадку можна одержа-
виразів з коренями слід дуже обережно, обов’язково перевіряючи виконання умов, за яких вони справ- джуються. У супротивному випадку можна одержа-
ти неправильний результат. Наприклад 4 a2 = a лише при а ≥ 0.
При від’ємних значеннях а ця рівність є неправильною. Щоб пе- реконатись у цьому, підставте, наприклад, а = –1, і подивіться, якого вигляду набуде права частина рівності.
Якщо а < 0, то для застосування властивості 4 необхідно спо- чатку перетворити корінь: 4 a2 = 4 (−a)2 . Оскільки – а > 0, то до

Корені п-го степеня |
93 |
останнього кореня можна застосувати властивість 4: |
4 a2 = |
= 4 (−a)2 = −a.
Приклад 11. Винести множник з-під знака арифметичного кореня: 1) 4 6a13b6 (a > 0,b > 0); 2) 4 6a13b6 (a > 0,b < 0).
1) 4 6a13b6 = 4 6a12 a b4 b2 = 4 a12 4 b4 4 6ab2 = a 3 b 4 6ab2 =
= a3b4 6ab2 , оскільки a > 0,b > 0.
2) 4 6a13b6 = 4 a12 4 b4 4 6ab2 = a 3 b 4 6ab2 = −a3b4 6ab2 , оскіль-
ки a > 0,b < 0.
Відповідь. 1) a3b4 6ab2 ; 2) −a3b4 6ab2 .
Приклад 12. У виразі b4 a внести множник під знак кореня, якщо b < 0.
Оскільки b < 0 і b = 4 b4 , то −b = 4 b4 . Таким чином, b4 a =
=−4 b4 4 a = −4 b4a , згідно із властивістю 2.
Відповідь. −4 b4a .
99 Контрольні запитання
1°. Які з наступних чисел є арифметичними коренями відповід- ного степеня:
|
а) |
3 −25; |
б) 5 25; |
в) |
4 23; |
|
г) 4 (−7)2 ? |
|
||||
2°. |
Як записати корінь п-го степеня з від’ємного числа через |
|||||||||||
|
арифметичний корінь того самого степеня: |
|
|
|
|
|||||||
|
а) |
3 −15; |
б) 5 −37; |
в) |
7 −23; |
г) 9 −7 ? |
|
|||||
3. |
Чому дорівнює значення виразу: |
|
|
|
|
|
|
|
||||
|
а°) ( 3 −15)3 ; |
б°) 4 74 ; |
в) |
5 (−37)5 ; |
г) 10 (−5)10 ? |
|
||||||
4°. |
Чому дорівнює значення виразу: |
|
|
|
|
|
|
|
||||
|
а) |
3 8 27 125; |
б) 3 1000 |
1 |
|
64; |
в) |
4 16 81 10000; |
||||
|
27 |
|
||||||||||
|
|
3 27 ; |
ґ) 3 1000 ; |
|
|
81 |
|
|
81 |
|
|
|
|
г) |
д) |
4 |
; |
е) 4 |
|
? |
|||||
|
|
0,0256 |
|
|||||||||
|
|
64 |
216 |
|
|
625 |
|
|
|
|
||
5°. |
До якого спільного показника слід звести корені при множен- |
|||||||||||
|
ні або діленні: |
|
|
|
|
|
|
|
|
|
|
|
|
а) 3 2 і 6 3; |
б) 3 2 і 4 3; |
в) |
4 2 і 6 3; |
г) 10 2 і 15 3 ? |
|||||||

94 |
Розділ 1. Функції, їхні властивості та графіки |
6.За яких значень букв, що входять до виразів, справджується рівність:
а) |
4 |
a4 = a ; |
б) |
4 |
a4 = −a ; в) 3 |
a3 |
= a ; г) |
ab = −a −b ? |
7*. Чи правильною є рівність: |
|
|
|
|||||
а) |
|
a3b = a ab; |
|
|
б) 3 a4b = a3 ab; |
в) |
a3b2 = ab a ? |
|
Задачі
82°.Вкажіть проміжки, на яких зростає і на яких спадає функція:
|
1) |
y = x3 ; |
|
|
2) y = x4; |
|
|
|
|
|
3) y = −x3 ; |
|
||||||||||||||
|
4) |
y = −x4; |
|
|
5) y = (1 − x)6 ; |
|
|
|
6) y = (x + 2)5 . |
|
||||||||||||||||
83. |
Дослідіть на парність і непарність функцію: |
|
|
|
|
|||||||||||||||||||||
|
1°) |
y = x4 + 2; |
|
|
|
|
|
2°) |
y = −x5 + 2x3 − x; |
|
||||||||||||||||
|
3°) |
y = |
|
4x5 |
; |
|
|
|
|
|
4) |
y = x3 + x2 + x +1. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
84. |
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Побудуйте графік функції: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1°) |
y = (x −2)3 ; |
|
|
2°) y = x3 −2 ; |
3) |
y = (x −3)4 + 2 . |
|||||||||||||||||||
85. |
Скільки розв’язків має рівняння: |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
1°) |
x3 = 3 − x ; |
2°) |
|
x = x4 ; |
|
3°) x5 +1 = |
; |
|
4) х3 = |x|? |
|
|||||||||||||||
86. |
Розв’яжіть рівняння: |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
|
3) х4 = 625; |
|
|
|
4) х4 = –625. |
||||||||||||||||||||
|
1) х3 = 64; |
2) х3 |
= –64; |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87°.Знайдіть значення виразу: |
|
|
|
|
91 |
|
|
|
|
|
|
|
|
|||||||||||||
|
1) |
3 2 3 500 ; |
2) 4 324 4 4 ; |
|
3) |
3 −1 |
|
; |
|
|
4) 3 36 49 |
; |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
|
||
|
5) |
5 |
710 |
|
|
; |
|
|
6) 3 0,027 36 ; |
7) |
4 48 27 ; |
|
|
8) |
5 162 48 . |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88°.Подайте вираз у вигляді дробу: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1) |
3 |
8 |
; |
2) |
3 64; |
3) |
4 |
|
5 |
; |
4) 4 625; |
|
5) 5 |
6 |
. |
||||||||||
|
|
81 |
|
|
||||||||||||||||||||||
|
|
27 |
|
|
|
|
|
15 |
|
|
|
256 |
|
|
|
a5 |
|
|||||||||
89°.Обчисліть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 . |
||||||||
|
1) |
3 243 : 3 9; |
|
2) 3 256 : 3 4; |
|
3) |
3 250 : 3 2; |
|
|
4) |
3 48 : 3 |
|||||||||||||||
90. |
Подайте вираз у вигляді кореня з деякого числа: |
|
|
4 |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
1°) |
3 3 5; 2°) 4 |
3 10 ; 3°) 3 |
4; |
|
4°) |
4 5 12; 5) |
3 2 5; 6) 5 43 3. |
||||||||||||||||||

Корені п-го степеня |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95 |
|||||
91. |
Розв’яжіть рівняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1) 4 x −0,2 = 0 ; 2) 8 x +3 = 0 ; |
3) |
3 x −2 = 0; |
4) 3 x +3 = 0 . |
||||||||||||||||||||
92. |
Спростіть вираз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1°) |
3 1 b3 ; |
|
|
2°) |
|
5 243d15 ; |
3) |
4 16a4 , a > 0 |
;4) |
4 16 c4 |
,c < 0 . |
||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
|
|
|
|
|
93. |
Скоротіть дріб: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
7 + 7 |
|
|
|
|
a −1 |
|
a −81b |
|
8a −1 |
|
|
|||||||||||
|
1°) |
7 +1 ; |
|
|
2°) |
|
|
|
; |
|
3) |
|
; |
4) |
|
|
|
|
. |
|||||
|
|
|
|
|
a +1 |
a −9 b |
|
|
||||||||||||||||
94. |
|
|
|
43 a2 |
|
+ 23 a +1 |
||||||||||||||||||
Винесіть множник з-під знака кореня: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1°) |
3 250; |
|
|
2°) 4 405; |
|
|
3) |
3 54a7 ; |
4) 4 32b6 |
; |
|
|
|||||||||||
|
5) 4 5a6 , a < 0; 6) 3 m8n2 ; |
7) |
4 16a3b11 . |
|
|
|
|
|
|
|
|
|||||||||||||
95. |
Внесіть множник під знак кореня: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1°) |
−55 5 ; |
|
|
2) b6 2,b ≤ 0 ; |
3) |
ab4 2, a ≥ 0,b ≤ 0 ; |
4) b4 −b . |
||||||||||||||||
96. |
Спростіть вираз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1°) 2 5 −2 |
45 + 2 20 ; |
|
|
|
2°) 3 40 + 4 162 −34 2 −23 5 ; |
|
|
||||||||||||||||
|
3°) 43 6 + 3 135 − 3 384 − 3 40 ; |
4°) ( 12 + 75 + 27 ): |
|
15 ; |
|
|
||||||||||||||||||
|
5) (3 4 −33 2)(3 16 +33 8 + 93 4);6) (4 3 − 4 27 )(4 3 + 4 27 ); |
|
|
|
||||||||||||||||||||
|
7) (4 3 − 4 27)2 −4 3 ; |
|
|
|
8) |
(7 6 |
6 −64 216 )4 . |
|
|
|
|
|
|
|||||||||||
97. |
Знайдіть область визначення функції: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1°) |
y = 4 5x −15; 2°) |
y = 3 x2 −1; |
3°) |
y = |
x2 −1; |
4) |
y = |
5 |
|
|
x |
. |
|
||||||||||
|
|
x +1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
98. |
Потік рідини через поперечний переріз труби обчислюється за |
|||||||||||||||||||||||
|
|
|
|
|
πR4 |
|
p |
− p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
формулою: |
Q = |
8η |
|
1 |
|
2 |
,деQ —потік,R —радіуструби,l— |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
довжина труби, р1 – р2 |
— різниця тисків на кінцях труби, η — |
||||||||||||||||||||||
|
в’язкість рідини. Виразіть радіус труби R через інші змінні. |
|
|
|||||||||||||||||||||
99. |
Перший член геометричної прогресії дорівнює 2. Чому дорів- |
|||||||||||||||||||||||
|
нює її знаменник, якщо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1) сьомий її член дорівнює 1458; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2) добуток її шести перших членів дорівнює 728; |
|
|
|
|
|
|
|
||||||||||||||||
|
3*) добуток її перших п членів дорівнює Pn? |
|
|
|
|
|
|
|
|
|||||||||||||||

96 Розділ 1. Функції, їхні властивості та графіки
Вправи для повторення
100. Побудуйте графік функції:
1) y = |
3 |
; |
2) y = 3 x −2; 3) y = x5 + 2; |
4*) y = |
x −1 |
. |
|
x + 2 |
|
|
|
x −1 |
|
101.Знайдіть множини значень функцій, заданих у задачі 100.
102.В яких точках графіки функцій, перелічених у задачі 100, перетинають осі координат?
Підсумок
Основні поняття
Означення |
Приклади |
Застосування |
||||||
Коренем n-го степе- |
|
|
|
|
Операція |
добування |
||
3 −27 = −3 |
||||||||
ня (n Ν, n > 1) з |
кореня n-го степеня є |
|||||||
Корінь |
четвертого |
|||||||
числа |
а називається |
оберненою для опера- |
||||||
число, |
n-ий степінь |
степеня з числа 81 |
ції піднесення до n-го |
|||||
якого дорівнює а. |
дорівнює 3 або –3. |
степеня. |
|
|||||
|
|
|
|
|
|
|
||
Арифметичним ко- |
3 1 = |
1 , 4 81 = 3. |
Поняття |
арифметич |
||||
ренем |
п-го степеня із |
ного кореня приводить |
||||||
невід’ємного числа а |
8 |
|
2 |
|
до однозначності зна- |
|||
називають невід’ємне |
|
|
|
|
ходженняневід’ємного |
|||
число, |
п-ий степінь |
|
|
|
|
кореня з невід’ємного |
||
якогодорівнюєа. |
|
|
|
|
числа . |
|
||
Головні твердження
|
|
|
|
|
|
|
|
Арифметичний корінь п-го степеня з добут- |
|
|
|
|
|
|
|
ку двох невід’ємних чисел дорівнює добутку |
n |
ab = |
n |
a |
n |
b, |
|
арифметичних коренів п-го степеня з цих |
|
|
|
|
|||
|
а ≥ 0, b ≥ 0. |
||||||
чисел. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Арифметичний корінь п-го степеня з дро- |
|
|
|
|
|
|
|
бу, чисельник якого невід’ємний, а знамен- |
|
n a |
= n a |
, |
|
||
ник — додатний, дорівнює арифметичному |
|
|
|||||
кореню п-го степеня із чисельника, поділе- |
|
b |
|
n b |
|
|
|
ному на арифметичний корінь п-го степеня |
|
а ≥ 0, b > 0. |
|||||
зі знаменника. |
|
|
|
|
|
|
|
Якщо показник кореня і показник степеня |
|
n k a = nk a, |
|||||
підкореневого виразу помножити або поді- |
|
||||||
лити на те саме натуральне число, то зна- |
nk amk |
= n am , |
|||||
чення кореня не зміниться. |
|
а ≥ |
0. |
|
|
|
|
