
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач

§15. Властивості і графіки тригонометричних функцій
У цьому параграфі буде розглянуто властивості тригонометричних функцій, побудовано їхні графіки. Ðозглядатиметься специфічна властивість цих функцій — періодичність. Ïеріодичні функції описують різні ситуації (астрономічні явища, життєдіяльність організму тощо), які періодично повторюються. Ðозглядаються гармонічні коливання, які описуються періодичними функціями.
1. Періодичні функції
 При введенні тригонометричних функцій аргумент
При введенні тригонометричних функцій аргумент 
 позначався буквою t, оскільки букви х і у використовувались для позначення координат точки Pt . Те-
позначався буквою t, оскільки букви х і у використовувались для позначення координат точки Pt . Те-
пер повернемось до звичних позначень: х — незалежна змінна, у — залежна змінна, тобто у = sin х, у = cos х, y = tg x.
Оскільки числам х, х ± 2π на тригонометричному колі відповідає одна й та сама точка Px , то мають місце рівності:
sin(x ± 2π) = sin x, cos(x ± 2π) = cos x .
Цю властивість функцій у = sin х і у = cos х називають періодичністю. Вона полягає у тому, що значення функції повторюються через рівні проміжки зміни аргументу. Точний зміст поняття періодичності функції міститься у наступному означенні.
Функція у = f(х) називається періодичною, якщо існує таке число T ≠ 0, що область визначення функції
разом з кожною точкою х містить точки х ± Т і при цьому виконується рівність f(х ± Т) = f(x). Число Т називається періодом функції.

Властивості і графіки тригонометричних функцій |
267 |
!Звертаємо увагу на те, що рівність f(х ± Т) = f(x) має справджуватисьдлявсіхзначеньхізобластівизначення
функції. Для окремих функцій можна вказати числа, додавання яких до одного значення аргументу не змінює значення функції, водночас додавання до іншого значення аргументу — змінює. Такі числа не є періодами функції.
|
π |
|
= sin |
3π |
= −1 |
, |
Наприклад, sin 0 = sin (0 + π) = 0, але вже sin |
+ π |
2 |
||||
в той час коли sin π |
2 |
|
|
|
|
|
=1 . Отже, число π не є періодом функції |
||||||
2 |
|
|
|
|
|
|
у = sin х. |
|
|
|
|
|
|
Функції у = sin х і у = cos х є періодичними з періодом 2π. Цей факт використовувався у § 14 при обчисленні значень синуса і косинуса.
Періодомтангенсаікотангенсаєчислоπ,щовипливаєзформул зведення: tg(t + π) = tg(t – π) = tg t.
Якщо число Т є періодом функції у = f(x), то числа 2Т, 3Т, … і взагалі пТ, п Z, п ≠ 0, також є її періодами. Справді, наприклад, f(х + 2Т) = f((x + Т) + Т) = f(х + Т) = f(х). Звідси випливає, що періодами функцій у = sin х і у = cos х є числа 4π, 6π, … , а періодами функцій у = tg х і у = ctg х є числа 2π, 3π, 4π … .
На графіку функції її періодичність з періодом Т відображається наступним чином.
Якщо графік періодичної функції з періодом Т паралельно перенести на Т одиниць уздовж осі абсцис у додатному чи від’ємному напрямах, то він перейде сам у себе.
На рис. 305 зображено графік періодичної функції з періодом l.
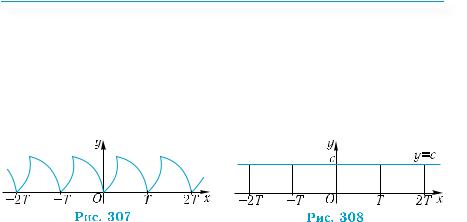
Для побудови графіка періодичної функції з періодом Т достатньо побудувати його на відрізку завдовжки Т (рис. 306), а потім
268 |
Розділ 3. Тригонометричні Функції |
побудований графік паралельно перенести вздовж осі абсцис в обох напрямах на відстані Т, 2Т, 3Т і т. д. (рис. 307).
Стала функція, що визначена на всій числовій осі, є періодичною. Її період — будь-яке число, відмінне від нуля. Справді, для сталої функції у = с справджується очевидне співвідношення: у(х + Т) = с = у(х) для будь-якого дійсного х при будь-якому Т ≠ 0 (рис. 308).
Періодичними функціями описуються різні фізичні процеси: маліколиваннямаятника,обертанняпланетнавколоСонця,сила змінного струму тощо. Найпростішим приладом для ілюстрації періодичних процесів є годинник. Положення кінців стрілок повторюються через рівні проміжки часу. Для секундної стрілки цей проміжок складає 60 с, для хвилинної — 60 хв, для годинної —
12 год.
Ïðèê ëàä 1. Нехай функція y = f(x) є періодичною з періодом 3 і f(1) = 2. Чому дорівнює f(–8)?
По-перше, зазначимо, що функція y = f(x) визначена при
х = –8, бо, за означенням періодичної функції, область визначення
даної функції разом з точкою х = 1 містить точки: 1 – 3 = –2, –2 – 3 =
= –5, –5 – 3 = –8. По-друге, f(–8) = f(–8 + 3) = f(–5) = f(–5 + 3) = f(–2) = = f(–2 + 3) = f(1) = 2.
Відповідь. 2.
Приклад 2. Довести, що періодом функції y = sin2x є число π. Функція y = sin2x визначена на всій числовій осі. Тому її
область визначення разом з кожною точкою х містить точки х ± π. Підставимо замість х у вираз для цієї функції х + π:
sin (2(x + π))= sin (2x + 2π) = sin2x. Той самий результат одержи-
мо, якщо замість х у вираз для цієї функції підставити х – π. За означенням, число π є періодом функції y = sin2x .

Властивості і графіки тригонометричних функцій |
269 |
З того, що кожній точці на тригонометричному колі 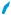
 відповідає безліч чисел, які відрізняються одне від одного на 2πk, k Z, випливає, що тригонометричні функції у = sin х і у = cos х для чисел х + 2πk при
відповідає безліч чисел, які відрізняються одне від одного на 2πk, k Z, випливає, що тригонометричні функції у = sin х і у = cos х для чисел х + 2πk при
всіх k Z набувають того самого значення: sin (х + 2πk) = sin х, cos(х + 2πk) = cos х, тобто періодами функцій у = sin х і у = cos х є числа 2πk, k ≠ 0, k Z. Усі ці періоди кратні 2π. Природно виникає запитання: «Чи існують інші додатні періоди цих функцій, менші від 2π?» Відповідь на нього дає наступне твердження.
Теорема 1. Найменшийдодатнийперіодфункційу=sin х і у = cos х дорівнює 2π.
|
Покажемо, що інших періодів, окрім чисел 2πk, k Z, k ≠ 0, ці |
|
функції не можуть мати. Справді, якщо |
Т — період функції у = sin х, |
|
то |
sin (x +T ) = sin x для будь-якого х, |
зокрема для х = 0, тобто |
sinT = sin 0 = 0 .Алеsin Т перетворюється на нуль при Т = 0; Т = π; |
||
Т |
= 2π і, взагалі, при Т = πп, п Z, і тільки при цих значеннях. |
|
Число π не є періодом розглядуваної функції. Справді, sin π |
=1, |
||||||
π |
|
|
3π |
|
2 |
|
|
= sin |
= −1 |
, тобто існує значення х із області визначен- |
|||||
sin |
+ π |
2 |
|||||
2 |
|
|
|
|
|
||
ня функції, таке, що sin (x + π) ≠ sin x . Отже, найменшим додатним
періодом функції у = sin х є число 2π.
Доведення того, що 2π — найменший додатний період косинуса,
аналогічне.
Подібне твердження справджується для функцій у = tg х
і у = сtg х.
Теорема 2. Найменший додатний період функцій у = tg х і у = сtg х дорівнює π.
Із формул зведення випливає, що числа πk, k Z, k ≠ 0, є періодами функцій у = tg х і у = ctg х. Оскільки tg х при
|
π |
π |
|
перетворюється на нуль при х = 0 або при х = π |
||
x 0; |
2 |
|
|
2 |
; π |
|
|
|
|
|
|
||
і тільки в цих точках, то не існує додатного числа, меншого від π,
яке б могло бути періодом тангенса. Отже, найменшим додатним періодом функції у = tg х є число π. Доведення того, що π — найменший додатний період котангенса, аналогічне. Рекомендуємо про-
вести його самостійно.

270 |
Розділ 3. Тригонометричні Функції |
Найменший додатний період періодичної функції називають основним періодом цієї функції. Всі інші її періоди кратні основному періоду. Для функцій у = sinх і у = cos х основний період дорівнює 2π, а для функцій у = tg х і у = ctg х основний період дорівнює π. Найпростішим прикладом періодичної функції, яка не має основного періоду, є стала функція, визначена на всій числовій осі.
Ïðèê ëàä 3 . Знайти основний період функції у = sin 3х.
Областю визначення даної функції є числова вісь. Числа
|
2πn |
|
, n Z, — періоди для функції у = sin3х: |
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2πn |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin3 x + |
|
= sin(3x + 2πn) = sin3x . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Якщо Т — довільний додатний період для sin3х, то sin3(х + Т) = |
||||||||||||||||
= sin3х при кожному |
х, оскільки число 3Т |
теж є періодом даної |
|||||||||||||||
функції. |
Беручи |
x = |
π |
|
π |
+T |
|
|
π |
=1 |
, |
або |
|||||
6 |
, матимемо: sin3 |
6 |
= sin |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
π |
|
|
Проте |
синус дорівнює |
одиниці |
лише |
|
при |
|||||||
sin |
2 |
+3T =1 . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x = π + 2πn, n Z . Тому π +3T = |
π + 2πn, 3T = 2πn, T = |
2πn ,n Z . |
||||
2 |
2 |
2 |
|
|
3 |
|
Серед чисел 2πn |
найменшим додатним числом є число |
2π , |
||||
3 |
|
|
2π |
|
|
3 |
тобто основний період функції sin 3х дорівнює |
. |
|
|
|||
|
|
|
||||
|
|
3 |
|
|
|
|
Відповідь. 23π .
Аналіз прикладу 3 підказує наступну властивість періодичних функцій і містить ідею її доведення.
Теорема 3. Якщо функція f є періодичною з основним періодом Т, то функція у = Af(kx + b) + l, де А, k ≠ 0, b, l —
деякі числа, також є періодичною, причому її основний період дорівнює Tk .
Результат розв’язання прикладу 3 узгоджується зі сформульованою властивістю: основний період функції у = sin 3х до-

Властивості і графіки тригонометричних функцій |
271 |
рівнює 23π . Із цієї властивості випливає, що основні періоди функ-
цій y = sin 4x, y = cos x2 , y = tg 2x відповідно дорівнюють 24π = 2π ,
2π : 12 = 4π , 2π .
Контрольні запитання
1°. Чи є правильним твердження: якщо періодична функція в якійсь точці набуває значення 1, то цього значення вона набуває у безлічі точок?
2°. Чи є число 3π періодом функції у = sin х? 3°. Чи є число 5π періодом функції у = tg х?
4.Який основний період має функція: a) sin 5х; б) cos 3x ; в) sin πх?
5.Чому дорівнює f(–9), якщо функція y = f(x) є періодичною з періодом 5 і f(1) = 0?
6*. Чи є функція y = cos x періодичною?
7.Чи може бути періодичною функція, яка зростає на всій області визначення?
2. Властивості та графіки функцій у = sin х і у = cos х
Розглянемо найпростіші властивості функцій у = sin х і у = cos х, користуючись означеннями синуса і косинуса, і побудуємо їхні графіки.
Властив³сть 1. Функції у = sin х і у = cos х визначені на
всій числовій осі.
Справді, кожному дійсному числу х можна поставити у відповідність точку тригонометричного кола. Абсциса цієї точки є ко-
синусом числа х, а ордината – синусом числа х.
Властив³сть 2. Функції у = sin х і у = cos х — періодичні з найменшим додатним періодом 2π.
Цю властивість доведено у попередньому пункті.
Властив³сть 3. Нулями функції у = sin х є числа πn, n Z, а нулями функції у = cos х — числа 2π + πn,n Z.
272 |
|
|
|
|
|
|
|
|
Розділ 3. Тригонометричні Функції |
||||||||||
Нулі функції у = sin х – це числа, яким відповідають точки |
|||||||||||||||||||
на тригонометричному колі з ординатою 0, а саме: …, –3π, –2π, –π, |
|||||||||||||||||||
0, π, 2π, 3π, ... і взагалі числа πn, |
n Z. Аналогічно нулі функції |
||||||||||||||||||
у = cos |
х — це числа, яким відповідають точки на тригонометрич- |
||||||||||||||||||
ному колі з абсцисою 0, а саме: …, |
−3π, − π |
, π |
, 3π,... і взагалі чис- |
||||||||||||||||
ла π + πn,n Z. |
|
|
|
|
|
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
4. Функція у = sin х — не- |
|
|
|
|
|
|
|
|
|||||||||
Властив³сть |
|
|
|
|
|
|
|
|
|||||||||||
парна, а функція у = cos х — парна, тоб- |
|
|
|
|
|
|
|
|
|||||||||||
то для кожного х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
sin(–х) = –sin х, cos(–х) = cos х. |
|
|
|
|
|
|
|
|
|
|||||||||
За побудовою, точки Pt і P–t |
симетрич- |
|
|
|
|
|
|
|
|
||||||||||
ні відносно осі абсцис (рис. 309). Їхні аб- |
|
|
|
|
|
|
|
|
|||||||||||
сциси збігаються, а ординати протилежні. |
|
|
|
|
|
|
|
|
|||||||||||
Тому при t = x: |
|
|
|
cos(−x) = cos x . |
|
|
|
|
|
|
|
|
|
||||||
sin(−x) = −sin x; |
|
|
|
|
|
|
|
|
|
||||||||||
Властив³сть |
5. Функція у = sin х додатна на інтервалі (0; π) |
||||||||||||||||||
і від’ємна на інтервалі (π; 2π); функція у = cos х додатна на |
|||||||||||||||||||
|
|
π |
; |
π |
|
|
|
|
|
|
|
|
π |
; |
3π |
|
|
|
|
інтервалі − |
2 |
2 |
і від’ємна на інтервалі |
2 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
Цю властивість обґрунтовано у § 14. |
|
|
|
|
|
|
|
|
|
||||||||||
Властив³сть |
6. |
|
|
|
|
|
|
|
|
|
|
|
|
π |
; |
π |
|
||
|
Функція у = sin х на проміжку − |
2 |
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
π |
; |
спадає. Функція у = cos х |
|||||||||||
зростає, а на проміжку |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
спадає на проміжку [0; π] і зростає на проміжку [π; 2π]. |
|
||||||||||||||||||
Ця властивість випливає з геометрич- |
|
|
|
|
|
|
|
|
|||||||||||
ного змісту синуса і косинуса. Якщо t |
зростає |
|
|
|
|
|
|
|
|
||||||||||
від − π |
до π , то ордината точки Рt |
зростає від |
|
|
|
|
|
|
|
|
|||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
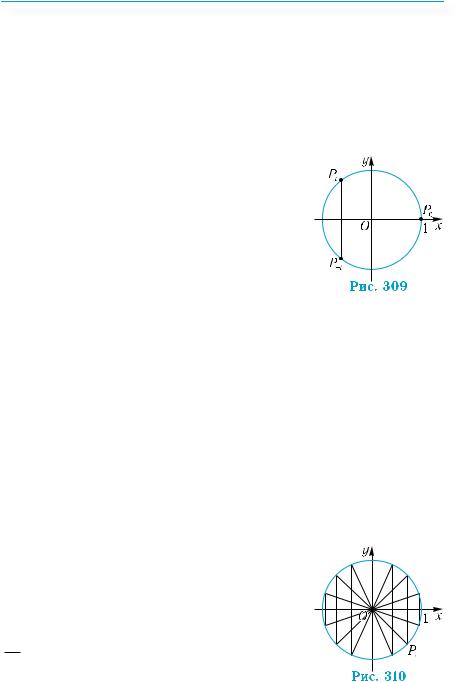
–1 до 1 (рис. 310). Якщо ж t зростає від π |
до |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3π , то ордината точки Р спадає від 1 до –1 |
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(див. рис. 310). Якщо t зростає від 0 до π, то |
|
|
|
|
|
|
|
|
|||||||||||

Властивості і графіки тригонометричних функцій |
273 |
абсциса точки Рt спадає від 1 до –1. Якщо ж t зростає від π до 2π, абсциса точки Рt зростає від –1 до 1 (див. рис. 310).
Властив³сть 7. Множиною значень функцій у = sin х
і у = cos х є відрізок [–1; 1].
За означенням синуса, |sin x| ≤ 1. Для довільного числа а
зпроміжку [–1; 1] існує щонайменше одна точка тригонометричного кола, ордината якої дорівнює а. Це означає, що функція у = sin х набуває всіх значень з проміжку [–1; 1]. Аналогічно обґрунтовується ця властивість для функції у = cos х.
Властив³сть 8. Функції у = sin х і у = cos х неперервні на
всій числовій осі.
Справді, при неперервній зміні значення х точка Px непе-
рервно переміщується по тригонометричному колу, а тому її координати cos х і sin х змінюються неперервно.
2π, то достатньо побудувати графік на відрізку [0; 2π], довжина |
|||
якого дорівнює періоду синуса. |
|
π |
|
Спочатку побудуємо графік на відрізку |
|
|
|
0; |
2 |
. На цьому |
|
|
|
|
|
Побудуємографікфункціїу=sinхзвикористаннямрозглянутих |
|||
властивостей синуса. Оскільки ця функція періодична з періодом |
|||
відрізку функція у = sin х зростає, sin 0 = 0, sin π =1 . Для знаход- |
|
2 |
π |
|
|
ження декількох точок графіка розіб’ємо відрізок 0; |
, наприк- |
|
2 |
лад, на 4 рівні частини. Візьмемо одиничне коло з центром у до- |
|
вільній точці осі абсцис (для зручності змістимо |
коло вліво |
(рис. 311)). Для побудови точки з абсцисою t знайдемо на колі точку Pt і через неї проведемо пряму, паралельну осі абсцис, до пере-
18 Математика, 10 кл.
274 |
Розділ 3. Тригонометричні Функції |
тину з прямою х = t. Точка перетину належатиме графіку функції у = sin х, оскільки її ордината збігається з ординатою точки Pt і дорівнює sin t.
Побудувавши таким чином усі 4 точки графіка і сполучивши їх, враховуючи зростання і неперервність функції, неперервною
кривою, одержимо ескіз графіка функції на відрізку |
|
|
π |
|
0; |
2 |
(див. |
||
рис. 311). |
|
|
|
|
|
|
|
|
|
Оскільки, за формулами зведення, sin(π −t) = sint , |
тобто ор- |
|||
динати точок t і π – t, симетричних відносно прямої x = |
π |
, дорів- |
||
|
|
2 |
|
|
нюють одна одній, то на проміжку |
π |
|
|
|||||||||||
|
;π точки графіка функції |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
||||
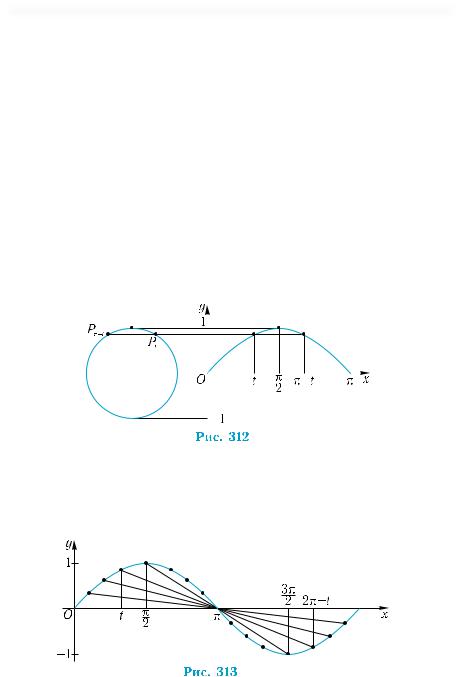
у = sin х розміщуються симетрично відносно точок графіка з про- |
||||||||||||||
|
π |
π |
(рис. 312). |
|||||||||||
міжку 0; |
|
відносно прямої x = |
2 |
|||||||||||
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки, за формулами зведення, sin(2π −t) = −sint , тобто ординати точок t і 2π – t протилежні одна одній, то на проміжку
[π;2π] точки графіка функції у = sin х розміщуються симетрично до точок графіка з проміжку [0;π] відносно точки (π; 0) (рис. 313).
Властивості і графіки тригонометричних функцій |
275 |
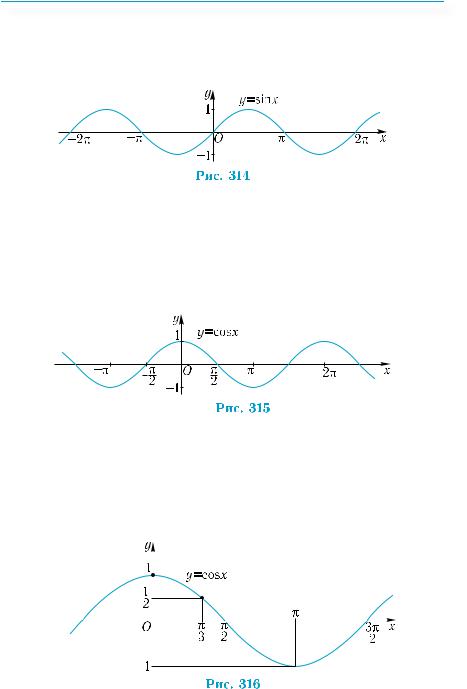
Користуючись правилом побудови графіка періодичної функції, за допомогою паралельних перенесень продовжимо графік на 2π, 4π, 6π, … вправо і вліво вздовж осі абсцис (рис. 314). Одержимо графік функції у = sin х. Він називається синусоїдою.
Оскільки |
π |
|
, то графік функції у = cos х |
|
cos x = sin |
2 |
+ x |
||
|
|
|
|
|
можна побудувати паралельним перенесенням графіка функції у = sin х у від’ємному напрямі вздовж осі х на
відстань 2π (рис. 315).
Ïðèê ëàä 4. Знайти найбільше і найменше значення функції
у= cos x на проміжку π; 3π .
3 2
Побудуємо графік функції у = cos x, відмітивши на осі абсцис
точки з абсцисами |
|
π |
і |
3π |
(рис. 316). Знайдемо на проміжку |
|||||||||
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18*
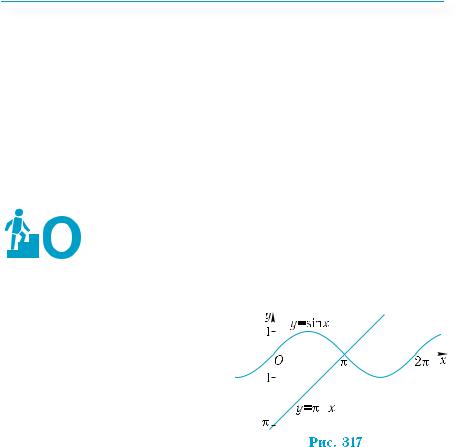
276 |
|
|
Розділ 3. Тригонометричні Функції |
||
|
π |
; |
3π |
найвищу і найнижчу точки графіка. Це відповідно точки з |
|
|
3 |
2 |
|
||
|
|
|
|
||
абсцисами |
π |
|
|
|
|
|
|
|
|
|
π |
π |
= |
1 |
|
і y(π) = cos π = |
||||||||||||
3 |
|
іπ.Ординатицихточок y |
|
= cos |
3 |
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
= –1 є найбільшим і найменшим значеннями функції на даному |
||||||||||||||||||||||||||||
проміжку, які вона набуває відповідно у точках |
π |
і π. |
|
|||||||||||||||||||||||||
Відповідь. 1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
; – 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Властивості та графіки синуса і косинуса дозволя- |
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
ють розв’язувати різноманітні завдання, пов’язані |
|||||||||||||||||||||||
|
|
|
|
|
з цими функціями, а саме: «читати» графіки, по- |
|||||||||||||||||||||||
|
|
|
|
|
рівнювати значення цих функцій, розв’язувати рів- |
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
няння, нерівності тощо. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
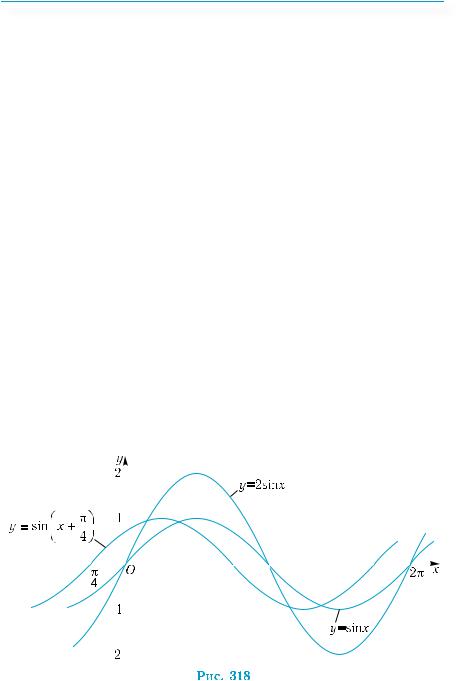
Приклад 5. Розв’язати рівняння: sin x = x – π. |
|
|
|
|
|
|
||||||||||||||||||||||
В одній системі коорди- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
нат побудуємо графіки функцій |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
у = х– π, у = sin |
х. Вони перети- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
наються в одній точці (рис. 317), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
як видно з графіків. Абсциса π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
точки перетину є розв’язком да- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ного рівняння. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Відповідь. х= π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ïðèê ëàä |
|
|
6 . Порівняти числа: 1) sin 2 і sin 3; 2) cos 5 і cos 6; |
|||||||||||||||||||||||||
3) cos π |
і sin |
|
3π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7 |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|||||
1) |
Оскільки |
< 2 < 3 < π |
, а на відрізку |
; |
функція |
|||||||||||||||||||||||
2 |
|
2 |
π |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = sin x спадає, то sin 2 > sin 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) Оскільки |
3π |
< |
5 < 6 < 2π, |
а на відрізку |
3π |
;2 |
|
функція |
||||||||||||||||||||
2 |
|
2 |
|
π |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = cos x зростає, то соs 5 < cos 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Властивості і графіки тригонометричних функцій |
277 |
3) За формулою зведення, sin |
3π |
π |
− |
π |
= |
cos |
π |
. Числа |
π |
||
8 |
= sin |
2 |
8 |
|
8 |
8 |
|||||
|
|
|
|
|
|
|
|||||
і |
π |
належать відрізку |
|
|
π |
, на якому функція у = cos х спадає. |
||||||
7 |
0; |
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Оскільки |
π < |
π , то |
cos π |
> cos π , тобто sin 3π |
> cos π |
. |
||||||
|
|
|
8 |
7 |
|
8 |
|
|
7 |
8 |
7 |
|
|
Відповідь. 1) sin2 > sin3; 2) соs 5 < cos 6; 3) sin 3π |
> cos π . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
7 |
Застосуємо до тригонометричних функцій перетворення графіків функцій, які розглядались вище, а саме: паралельне перенесення графіка вздовж координатних осей, стиск і розтяг графіка, симетричне відображення відносно координатних осей.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
Ïðèê ëàä 7. Побудувати графіки функцій: 1) y = sin x + |
; |
|||||||||||||||||||
2) у = 2 sinx; 3) у = sin 3х. |
|
|
4 |
|||||||||||||||||
π |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Графік функції y = sin x + |
можна одержати з графіка |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
π вліво |
||
у = sinх паралельним перенесенням уздовж осі х на |
||||||||||||||||||||
(рис. 318). |
|
4 |
|
|
||||||||||||||||
|
|
роз- |
||||||||||||||||||
|
2) Графік функції у = 2 sinх побудуємо із графіка у = sin х |
|||||||||||||||||||
тягом його від осі абсцис удвічі (див. рис. 318). |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

278 |
Розділ 3. Тригонометричні Функції |
3)Графік функції у = sin 3х є результатом стиску графіка
у= sin х до осі ординат утричі (рис. 319).
|
Контрольні запитання |
|
|
|
|
|
|
|
|
||||
1°. |
Чи має зміст запис: sin 2011? |
|
|
|
|
|
; б) 6 ; в) |
π ; г) |
π ? |
||||
2°. |
Чи може синус числа х дорівнювати: а) |
2 |
|||||||||||
3°. |
Чи є парними такі функції: |
|
|
|
|
|
7 |
2 |
6 |
||||
|
|
|
|
|
|
|
|
||||||
|
а) у = –cosх; |
|
б) |
y = sin2 t ; |
|
|
|
в) |
y = cos3 t ? |
|
|||
4°. |
Яке з чисел: cos 1°, cos 2°, cos 3°, ..., cos 100° є найбільшим? |
||||||||||||
5. |
За допомогою яких перетворень з графіка функції |
у = sin x |
|||||||||||
|
можна одержати графік функції: |
= 3sin x; |
г) у = sin x + 3? |
||||||||||
|
а) |
у = sin (x |
+ 3); |
б) у = sin 3x; |
в) у |
||||||||
6. |
Графік якої функції одержимо з графіка функції у = cos x: |
|
|||||||||||
|
а) паралельним перенесенням на 2 одиниці у додатному |
||||||||||||
|
напрямі вздовж осі абсцис; |
|
|
|
|
|
|
|
|
||||
|
б) паралельним перенесенням на 2 одиниці у від’ємному на- |
||||||||||||
|
прямі вздовж осі ординат; |
|
|
|
|
|
|
|
|
||||
|
в) стиском до осі абсцис удвічі; |
|
|
|
|
|
|
|
|
||||
|
г) розтягом від осі абсцис удвічі; |
|
|
|
|
|
|
|
|||||
|
ґ) симетричним відображенням відносно початку координат; |
||||||||||||
|
д) симетричним відображенням відносно осі ординат? |
|
|||||||||||
7. |
Якою є область визначення і множина значень функції: |
|
|||||||||||
|
а) |
у = sin(x – 1); |
б) |
у = cos x – 1; |
|
|
|
в) y = cos 2x; |
|
||||
|
г) |
у = 3sin x; |
ґ) |
у = cos (–x); |
|
|
|
д) y = –sin x? |
|
||||
8. |
Що більше: |
|
|
|
|
|
|
|
|
|
|
|
|
|
a) sin π чи sin π ; |
|
|
б) cos 40° чи cos 75°? |
|
|
|||||||
9. |
|
6 |
8 |
|
|
|
|
|
|
|
|
|
|
Зростає чи спадає функція у= cos х на відрізку: |
|
|
|||||||||||
|
а) [π ; 2π]; |
б) [0; π ]; |
|
π |
; |
5π |
|
г) [–2; –1]? |
|
||||
|
в) |
6 |
6 |
; |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||

Властивості і графіки тригонометричних функцій |
279 |
10*.Чому дорівнюють найбільше і найменше значення функції |
|||||||
у = sin x на проміжку: |
|
|
|
|
|||
|
4π |
; |
|
π |
; |
5π |
|
а) 0; |
|
б) − |
6 |
? |
|||
|
3 |
|
|
|
6 |
||
3. Властивості та графіки функцій y = tg x і y = ctg x |
|||||||
|
|
|
Розглянемо |
найпростіші |
|
властивості функцій |
|
|
|
|
|
||||
|
|
|
у = tg x і у= ctg x, користуючись їхніми означеннями, |
||||
|
|
|
і побудуємо їхні графіки. |
|
|
|
|
Властив³сть 1. Функція у = tg х визначена при всіх дійсних значеннях х, крім x = 2π + πk, k Z , а функція у = сtg х
визначенапривсіх дійсних значеннях х, крім x = πk, k Z .
Справді, функція у = tgx визначена при всіх значеннях х,
крім тих, при яких знаменник виразу tg х = sin x дорівнює нулю. cos x
А умову cos x = 0 якраз і задовольняють значення x = 2π + πk, k Z. Аналогічно доводиться друга частина властивості.
Властив³сть 2. Функції у = tg х і у = сtg х періодичні з найменшим додатним періодом π.
Цю властивість обґрунтовано у п. 1.
Властив³сть 3. Нулями функції у = tg х є числа πk, k Z, а нулями функції у = сtg х — числа x = π + πk, k Z .
Справді, нулі функції у = tg x збігаються2з нулями функції
у= sin х, а нулі функції у= ctg x – з нулями функції у = cos х (див.
п. 2).
Властив³сть |
4. Функції у = tg х і у = сtg х — непарні. |
|||||
Справді, |
tg(–х) = |
sin(−x) |
= |
−sin x |
= −tg x . Графік функції |
|
cos(−x) |
cos x |
|||||
|
|
|
|
|||
у = tg х симетричний відносно початку координат. Так само доводиться ця властивість для функції у= ctg x.
Властив³сть |
5. Функції у = tg х і у |
= сtg х додатні на інтер- |
|||
|
0; |
π |
|
π |
|
валі |
|
і від’ємні на інтервалі |
2 |
; π . |
|
|
|
2 |
|
|
|
280 Розділ 3. Тригонометричні Функції
Цю властивість обгрунтовано у § 14.
Властив³сть 6. Функція у = tg х зростає на проміжку
− π; π , а функція у = сtg х спадає на проміжку (0; π).
2 2
Ця властивість випливає з означень тангенса і котангенса.
Якщо х зростає від 0 до π , то чисельник дробу tgх = |
sin x |
зростає, |
||||||||||
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
cos x |
|
а знаменник спадає, тому функція у = tgx зростає на проміжку |
||||||||||||
|
π |
|
|
|
|
|
|
π |
|
випливає з непар- |
||
0; |
. Зростання функції на проміжку |
− |
2 |
;0 |
||||||||
|
2 |
|
|
|
|
|
|
|
= ctg х випливає з |
|||
ності цієї функції. Властивість для функції у |
||||||||||||
|
|
|
π |
+ x |
|
|
|
|
|
|
|
|
доведеного і рівності ctg x = –tg |
. |
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Властив³сть |
7. Множиною значень функцій у = tg х |
|||||||||||
і у = сtg х є множина всіх дійсних чисел. |
||||||||||||
Властив³сть |
8. Функції у = tg х і у = ctg х неперервні від- |
|||||||||||
|
|
|
π |
|
0; |
π |
|
|
|
|
|
|
повідно на проміжках 0; |
|
і |
2 |
. |
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Властивості 7 і 8 будуть обґрунтовані пізніше. |
||||||||||||
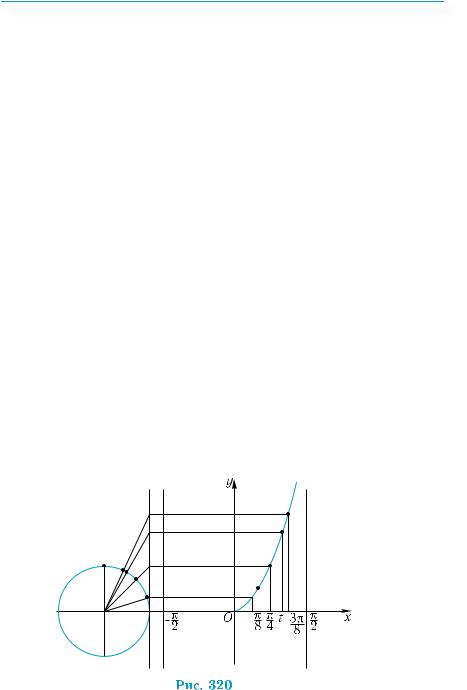
Розглянуті властивості функції у = tgx |
дозволяють побудувати |
|||||||||||
її графік, як і для функції у = sin х, у три етапи. На першому етапі
побудуємо графік на проміжку |
|
π |
. Для цього достатньо визна- |
|
0; |
2 |
|
||
|
|
|
|
|
чити декілька точок графіка і з’єднати їх неперервною лінією. Як
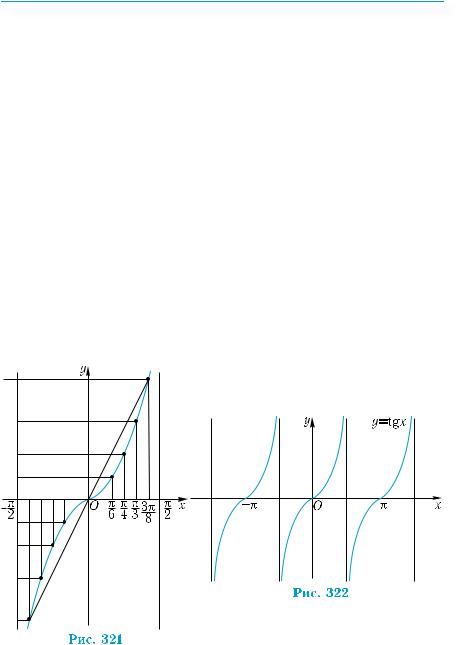
Властивості і графіки тригонометричних функцій |
281 |
|
π |
|
і при побудові синусоїди, розіб’ємо проміжок 0; |
на чотири рів- |
|
|
2 |
|
ні частини. Скориставшись лінією тангенсів, побудуємо чотири |
||
точки (рис. 320), які належать графіку функції |
|
π |
y = tgx, x 0; |
. |
|
|
|
2 |
Сполучивши точки (зважаючи на зростання і неперервність функ- |
||
ції) неперервною кривою, будемо мати ескіз графіка функції на
|
π |
|
|
|
|
|
проміжку 0; |
. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
− |
π |
; |
π |
за до- |
На другому етапі побудуємо графік на проміжку |
2 |
|
||||
|
|
|
|
2 |
|
|
помогою перетворення симетрії, скориставшись непарністю тан- |
||||||
генса (рис. 321). |
|
|
|
|
|
|
Тим самим одержали графік функції у=tg хна проміжку, довжина якого дорівнює найменшому додатному періоду тангенса π.
Оскільки функція тангенс є періодичною, то на третьому етапі її повний графік можна побудувати за допомогою паралельного перенесення одержаного графіка вздовж осі х на ±π; ±2π і т. д. (рис. 322). Графік функції tgх називають тангенсоїдою.
Графік функції у = ctg х можна одержати з графіка функції
|
π |
, |
|
у = tg х. Для цього, згідно з формулою зведення ctgx = −tg x + |
2 |
|
|
|
|
|
|

282 |
|
Розділ 3. Тригонометричні Функції |
достатньо графік функції у |
= tg х паралельно перенести у |
|
від’ємному напрямі осі х на |
π |
, а потім відобразити одержаний |
|
2 |
|
графік симетрично відносно осі абсцис. На рис. 323 тангенсоїду
зображено тонкою лінією, зсунуту тангенсоїду — штриховою, графік функції у = ctg х — жирною.
В остаточному вигляді графік функції у = ctg х зображено на рис. 324.
Ïðèê ëàä |
8 . Знайти абсциси точок перетину графіка функції |
|||||||||||||||||||||
у = tg х з прямою y = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Побудувавши графіки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функцій у |
= tg х і y = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(рис. 325), побачимо, що та |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
вітка графіка тангенса, яка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
відповідає |
проміжку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
π |
; |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
− |
2 |
2 |
, перетинає пряму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = |
|
3 |
у точці з абсцисою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x0 |
|
= |
π |
. Інші точки перетину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мають абсциси х0 + π; х0 – π, |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
х |
+ 2π, х – 2π і т. д. Отже, x = |
+ πk, k Z. |
||||||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Відповідь. 3π + πk, k Z.

Властивості і графіки тригонометричних функцій |
283 |
Властивість 6 про монотонність функцій у = tg х 
 і у = сtg х має просту геометричну інтерпретацію.
і у = сtg х має просту геометричну інтерпретацію.
Якщо х зростає від – 2π до 2π , то tg х, тобто координата
точки Вх, яка є точкою перетину прямої OPx з лінією тангенсів, зростає від –∞ до +∞ (рис. 326). Інакше кажучи, якщо х = 0, то tg х = 0, а
колихнаближаєтьсядо 2π ,залишаючисьменшимвід 2π ,tgхзростає і може набувати як завгодно великих значень.
Аналогічно,згеометричногозмістукотангенсавипливає,щоколи хзростає від 0 до π, координата точки Сх на лінії котангенсів, яка є точкою перетину прямої OPx з лінією котангенсів і дорівнює
сtgх, спадає від +∞ до –∞ (рис. 327). Інакше кажучи, якщо х = 2π , то сtgх = 0, а коли х наближається до 0, залишаючись більшим
від 0, значення сtgх зростає і може набути як завгодно великих значень.
Обґрунтуємо властивість 7 про множину значень функцій у = tg х і у = сtg х.
Доведемо, що довільне дійсне число а може бути значенням тангенса деякого числа. Розглянемо тригонометричне коло
і проведемо лінію тангенсів (рис. 328), по-  значивши на ній точку В(1; а). Сполучимо точки О і В та позначимо літерою Р точку перетину прямої ОВ з колом. Точка Р від-
значивши на ній точку В(1; а). Сполучимо точки О і В та позначимо літерою Р точку перетину прямої ОВ з колом. Точка Р від-
повідає деякому числу х, що належить
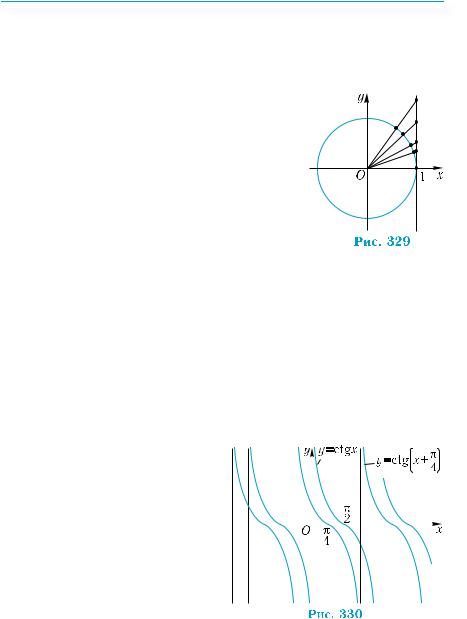
284 |
Розділ 3. Тригонометричні Функції |
проміжку − π; π ,їїкоординати— (cosх;sinх).ТомуР В=tgx=а.
2 2 0
Аналогічно властивість доводиться для у = сtg х.
Властивість 8, тобто неперервність, зокрема, функції у = tg х, випливає з того, що якщо дві точки на тригонометричному колі зближуються (відстань між ними стає як завгодно малою), то відповідні точки на осі тангенсів також зближуються (рис. 329). Аналогічно обґрунтовується ця властивість для функції у = сtg х. Нагадаємо, що неперервна функція описує процеси, які відбуваються плавно, тобто коли досліджувана величина за малий
проміжок часу змінюється мало (див. § 4).
Застосуємо до графіків функцій у = tg х і у = сtg х перетворення
графіків функцій, які розглядались вище, а саме: паралельне пе-
ренесення графіка вздовж координатних осей, стиск і розтяг гра- |
||||||||||||
фіка, симетричне відображення відносно координатних осей. |
|
|
|
|||||||||
Ïðèê ëàä |
9. |
|
|
|
|
|
|
|
|
π |
||
Побудувати графік функції: 1) y = ctg x + |
|
; |
||||||||||
2) y = ctg x – 1; 3) y = 2ctg x. |
|
|
|
|
|
|
4 |
|||||
π |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
1) Графік функції y = ctg x + |
можна одержати з графіка |
|||||||||||
|
|
|
4 |
|
|
|
||||||
функції у = ctgх паралельним |
|
|
|
|
|
|
|
|
|
|||
перенесенням |
його вздовж осі |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
абсцис у від’ємному напрямі осі |
|
|
|
|
|
|
|
|
|
|||
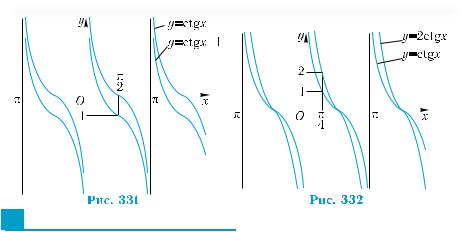
х на π (рис. 330). |
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2) Графік функції y = ctg x – 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
можнаотриматизграфікафунк- |
|
|
|
|
|
|
|
|
|
|||
ціїу=ctgх |
паралельнимперене- |
|
|
|
|
|
|
|
|
|
||
сенням його вздовж осі ординат |
|
|
|
|
|
|
|
|
|
|||
у від’ємному напрямі осі у на 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
(рис. 331). |
|
|
|
|
|
|
|
|
|
|
|
|
3) Графік функції y = 2ctg x можна одержати з графіка функції у = ctg х розтягом його від осі абсцис удвічі (рис. 332).
Властивості і графіки тригонометричних функцій |
285 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольні запитання |
|
|
|
|
|
|
|||||||||||||
1°. |
Чи має зміст запис: а) tg 2011; б) сtg 2011π? |
|||||||||||||||||||
2°. |
Чи є функція у = tg х |
зростаючою на проміжку: |
||||||||||||||||||
|
|
|
π |
; |
π |
; |
|
− |
π |
; |
π |
в) [0; π]; |
|
г) (3; 3,1)? |
||||||
|
a) − |
6 |
6 |
|
б) |
4 |
3 |
; |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3°. |
Чи справджується нерівність сtg x < 0 в усіх точках проміжку: |
|||||||||||||||||||
|
|
2π |
; |
5π |
|
|
π |
; |
3π |
|
π |
; |
3π |
г) (2; 2,5)? |
||||||
|
а) |
3 |
6 |
; |
б) |
2 |
|
4 |
; |
в) |
6 |
4 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4°. |
В яких точках функції у = tg х |
і у = ctg х дорівнюють нулю? |
||||||||||||||||||
5. |
Яку область визначення має функція: |
в) ctg (х – 2); |
||||||||||||||||||
|
а) y |
= tg x |
+ 1; |
|
б) у = tg (х |
– 1); |
|
|
||||||||||||
|
г) y |
= ctg x + 2; |
|
ґ) y = ctg 3x? |
|
|
|
|
|
|||||||||||
6. |
Чи можуть функції у = tg х і у = ctg х набувати значень |
|||||||||||||||||||
|
0,0000001; 2011; 10–20; 1020? |
|
|
|
|
|
|
|||||||||||||
7. |
Якою є множина значень функції: |
= сtg x – 1? |
||||||||||||||||||
|
а) y |
= tg(x |
+ 1); |
|
|
|
|
|
|
|
б) y |
|||||||||
8. |
Чи можна стверджувати, що котангенс |
спадає: |
||||||||||||||||||
|
а) на всій своїй області визначення; |
|
|
|
|
|||||||||||||||
|
б) на кожному інтервалі, який повністю лежить у його області |
|||||||||||||||||||
|
визначення? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9. |
Чому дорівнює найменший додатний період функції: |
|||||||||||||||||||
|
а) y = tg 2x; |
|
|
|
|
|
|
|
б) y = ctg x |
? |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
286 |
Розділ 3. Тригонометричні Функції |
4. Гармонічні коливання
Нехай по колу з радіусом А рухається точка зі ста- 
 лою кутовою швидкістю ω, тобто за одиницю часу
лою кутовою швидкістю ω, тобто за одиницю часу  точка повертається на кут ω рад. За t одиниць часу ця точка повернеться на кут ωt рад. У початковий момент часу точка займає положення M0, кут ВОМ0 дорівнює α рад (рис. 333). У момент часу t точка займе положення M, кут М0ОМ дорівнює ωt рад, кут ВОМ дорівнює (ωt + α) рад.
точка повертається на кут ω рад. За t одиниць часу ця точка повернеться на кут ωt рад. У початковий момент часу точка займає положення M0, кут ВОМ0 дорівнює α рад (рис. 333). У момент часу t точка займе положення M, кут М0ОМ дорівнює ωt рад, кут ВОМ дорівнює (ωt + α) рад.
ПозначимочерезМx іМу проекції точки М на осі х і у відповідно. Під час руху точки М по колу її проекція Мх на вісь х коливається
вздовж горизонтального діаметра
ВС завдовжки 2А, досягаючи то
крайнього правого положення В, то
 крайнього лівого положення С. Так само і її проекція Му на вісь у
крайнього лівого положення С. Так само і її проекція Му на вісь у
коливається вздовж вертикального діаметра DF, теж досягаючи то найвищого положення D, то найнижчого положення F. Встановимо закони
руху точок Мх та Му.
ПобудуємоодиничнеколозцентромвточціОіпозначимочерез Т точку перетину променя ОМ з цим колом. Координати точки Т = Pωt+α дорівнюють cos (ωt + α) і sin (ωt + α), а тому, із міркувань подібності, координати точки М визначаються формулами:
х = A cos(ωt + α), у = A sin (ωt + α).
Ці формули описують відхилення точок Мx і Му від точки О – центра кола. Вони задають закони руху точок Мx і Му, які
називаються гармонічними коливаннями.
Зазначимо, що при А = 1, ω = 1, α = 0 одержимо відповідно функції x(t) = cos t, y(t) = sin t.
Коливальні рухи широко розповсюджені в навколишньому середовищі. Уявлення про них дають і океанські хвилі, і маятникові годинники, і гойдалки, і нервові імпульси. З ними пов’язане поширення звуку і світла. Багато з цих явищ можна описати за допомогою гармонічних коливань.
Введемо деякі поняття, пов’язані з гармонічними коливаннями проекцій на координатні осі точки, що рівномірно рухається по колу з центром у початку координат. Точку О — середину відріз-

Властивості і графіки тригонометричних функцій |
287 |
ка, вздовж якого проходить гармонічне коливання, — називають
положенням рівноваги, число А — амплітудою коливання.
Амплітуда характеризує величину найбільшого відхилення від положення рівноваги.
Число ω, як відомо, є кутовою швидкістю обертання точки. За
2π одиниць часу точка повернеться на кут 2πω рад, при цьому її
проекції на вісь х і на вісь у виконають 22πωπ = ω повних коливань. Число ω, тобто кількість повних коливань за 2π одиниць часу, на-
зивається ще круговою частотою коливань.
Число α, яке характеризує початкове положення точки на колі,
називається початковою фазою коливання, ωt + α — фазою коливання.
Час Т, протягом якого точка М робить повний оберт, називаєть-
ся періодом гармонічного коливання. За період Т проекція Мх
точки М на вісь х двічі пройде всі свої можливі положення і повер-
неться в початкове положення. Винятком є лише граничні поло-
ження В і С (див. рис. 333), кожне з яких точка пройде один раз. |
|||||||||||||||
Оскільки за 2π одиниць часу координата точки робить |
ω по- |
||||||||||||||
вних коливань, то одне повне коливання вона робить за |
2π |
оди- |
|||||||||||||
ω |
|||||||||||||||
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|||
ниць часу, тобто Т = |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
ω |
|
|
|
|
|
|
|||||||
Величина, обернена до періоду коливання, |
|
||||||||||||||
|
|
|
1 |
|
= |
|
ω |
, |
|
|
|||||
|
|
|
|
|
|
T |
2π |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
називається частотою коливання. Вона показує, скільки по- |
|||||||||||||||
вних коливань здійснює координата точки за одиницю часу. |
|||||||||||||||
|
Графік закону гармонічного коливання у = A sin(ωt + |
||||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
α |
можна побудувати з графіка |
|||||||
|
+ α) = Asin ω t + |
ω |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
функції y(t) = sin |
t |
паралельним перенесенням |
||||||||||||
|
|||||||||||||||
уздовж осі абсцис на |
|
α |
|
одиниць у додатному напрямі осі, |
якщо |
||||||||||
|
|
||||||||||||||
|
|
|
ω |
|
|
> 0; розтягом від осі ординат в 1 |
|||||||||
α < 0, і у від’ємному, якщо α |
|||||||||||||||
ω |
|
|
|
|
|
ω |
|
|
|
|
|
ω |
|||
разів при 0 < ω < 1 або стиском до осі ординат у ω разів при ω > 1;
288 Розділ 3. Тригонометричні Функції
розтягом від осі абсцис у А разів, якщо А > 1, або стиском до осі
абсцис в |
1 |
|
разів. |
|
|
|
|
|
|
|
|||
A |
|
|
|
можна |
одержати |
з |
функції |
||||||
|
x = A cos(ωt + α) |
||||||||||||
Функцію |
|||||||||||||
y = Asin(ωt + α) , замінивши α на α + π . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Ïðèê ëàä |
|
10 . Побудувати графік закону гармонічного коливан- |
|||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
ня y = 5sin 2t + |
3 |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
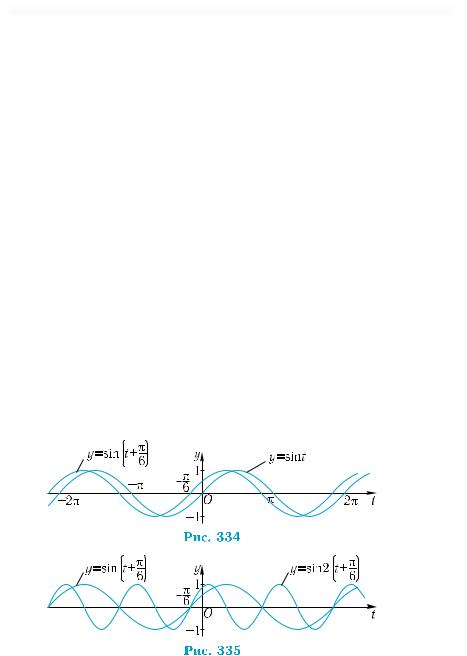
Подамо вираз для закону гармонічного коливання у вигля- |
|||||||||||||
|
|
|
|
2t + |
π |
|
|
|
π |
|
|
|
|
ді: y = 5sin |
3 |
= 5sin 2 |
t + |
. Графік будуємо у такій послі- |
|||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
довності: спочатку будуємо графік функції y = sin t (рис. 334), далі |
|||||||||||||
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
y = sin t + |
6 |
(паралельним перенесенням попереднього графіка |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
вздовж осі абсцис на π |
одиниць у від’ємному напрямі осі) (див. |
||||||||||||
|
|
|
|
|
|
6 |
|
|
π |
|
|
|
|
рис. 334), потім y = sin2 |
+ |
|
|
|
|||||||||
t |
6 |
(стиском попереднього графіка до |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
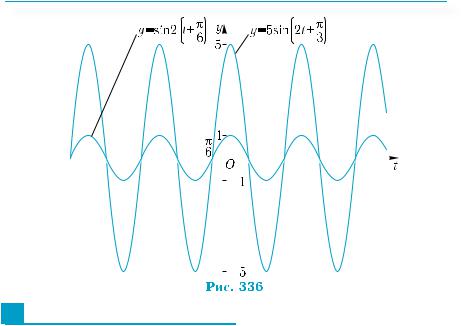
осі ординат удвічі) (рис. 335) і, нарешті, |
|
π |
(розтягом |
||||||||||
y = 5sin 2t + |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
попереднього графіка від осі абсцис у 5 разів) (рис. 336).
Властивості і графіки тригонометричних функцій |
289 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольні запитання
1°. |
Чому дорівнює амплітуда гармонічного коливання проекції |
|
|
на вісь х точки, що рівномірно рухається по колу з діаметром |
|
|
10 см з центром у початку координат? |
|
2°. |
Чому дорівнює кругова частота гармонічного коливання про- |
|
|
екції на вісь у точки, що рівномірно рухається по колу з цен- |
|
|
тром у початку координат з кутовою швидкістю 5 рад/с? |
|
3°. |
Чому дорівнює період гармонічного коливання проекції на |
|
|
вісь х точки, що рівномірно рухається по колу з центром у по- |
|
|
чатку координат з кутовою швидкістю 5 рад/с? |
|
4°. |
Чому дорівнює кутова швидкість руху точки по колу, якщо пе- |
|
|
ріод відповідного гармонічного коливання її проекції на вісь у |
|
|
дорівнює 4? |
|
5°. |
Чому дорівнює лінійна швидкість рівномірного руху точки по |
|
|
колу радіуса 2, якщо період відповідного гармонічного коли- |
|
|
вання її проекції на вісь х дорівнює 4? |
|
6. |
Відомо, що проекція точки, що рухається по колу з центром у по- |
|
|
чаткукоординат,навертикальнийдіаметрздійснюєгармонічне |
|
|
|
π |
|
коливання, яке визначається формулою y = 3sin 5t − |
. За |
|
|
6 |
|
яким законом змінюється проекція цієї точки на горизонталь- |
|
|
ний діаметр? |
|
19 Математика, 10 кл.
290 |
Розділ 3. Тригонометричні Функції |
7°. Чому дорівнює початкова фаза гармонічного коливання проекції на вісь х точки, що рівномірно рухається по колу з центром у початку координат , якщо її положення на колі в початковий момент часу збігається з верхнім кінцем вертикального діаметра?
Задачі
281°. Обчисліть:
1) cos173π ; 2) tg 3360°;
282°. Спростіть:
1)sin2 (α + 4π) + cos2 (α + 6π);
3)1+ ctg2 (α −7π);
283°. Доведіть рівність:
1) cos (t – π) = cos (t + π);
|
|
123π |
; |
4) ctg (–1950°). |
|
3) sin − |
4 |
|
|||
|
|
|
|
|
|
2) |
tg(α +3π) ctg(α −5π); |
||||
4) |
|
1 |
|
|
−1. |
cos2 (2α −8π) |
|||||
2) |
|
2t − |
π |
|
2t + |
2π |
||
tg |
3 |
|
= tg |
3 |
. |
|||
|
|
|
|
|
|
|
||
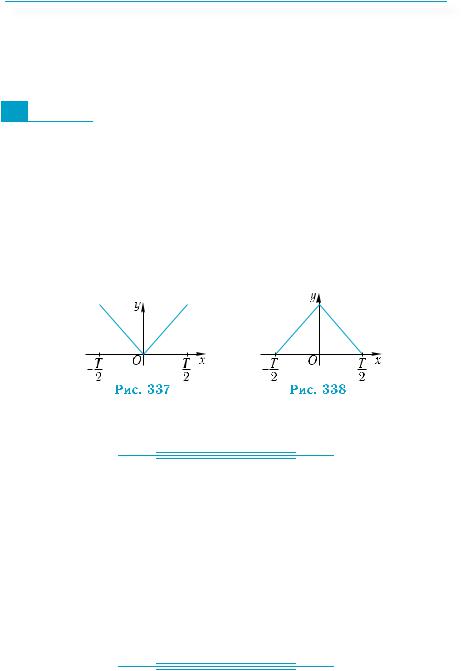
284.На рис. 337, 338 зображено частини графіків функцій з періодом Т.Побудуйтеграфікицихфункційнапроміжку[–2T;2T].
285.Доведіть, що число Т є періодом функції y = f(x), якщо:
1)y = cosx2 ,T = 4π; 2) y = sin2x,T = π; 3) y = ctgπx,T =1.
286.Доведіть, що функція f є періодичною, якщо:
1)f(x) = 1 + cos x; 2) f(x) = ctg 2x.
287.Знайдіть найменший додатний період, якщо він існує, для функції:
1) y = 2sin x |
; |
2) y = 3ctg |
3x |
; |
3) y = sin2 x + cos2 x . |
|
2 |
||||||
3 |
|
|
|
|

Властивості і графіки тригонометричних функцій |
291 |
288.Побудуйте графік функції y = sinx, x [−π;2π] і вкажіть на ньому точки, для яких:
1°) sin х = 1; |
2°) sin x = |
3 |
; |
3°) sin x = |
1 |
; |
|
2 |
3 |
||||||
|
|
|
|
|
4) sin х < 0; 5) sin х > 2 ; 6)sin х < −12 .
289.Побудуйте графік функції y = cosx, x [−2π; π] і вкажіть на ньому точки, для яких: 2
1°) cos х = –1; |
2°) cos х = – |
|
2 |
; |
3°) cos х = |
2 |
; |
|
||
2 |
5 |
|||||||||
|
|
1 |
|
|
2 |
|
||||
4) cos х > 0; |
5) cos x < |
; |
|
6) cosx > − |
|
. |
||||
2 |
|
2 |
||||||||
290. Розв’яжіть рівняння: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
1) sin x = 2 x ; |
|
2) cos x = – 2 x + 1. |
|
|
|
|||||
π |
|
|
|
|
|
π |
|
|
|
|
291. Знайдіть область визначення функції:
1) |
y = |
2sin x −3 |
; |
2°) |
y = |
1 |
; |
||
2 |
|
cos2 x +3 |
|||||||
|
|
|
|
|
|
|
|||
4) |
y = |
1 |
|
; |
|
5*) |
y = |
sin x ; |
|
cos x |
|
|
|||||||
|
|
|
|
|
|
|
|
||
3) |
y = |
|
1 |
|
; |
|
sin x −1 |
||||||
6*) |
y = |
1 |
|
. |
||
cos x |
||||||
|
|
|
|
|||
292.Які з функцій є парними, які — непарними, а які — ні парними, ані непарними:
1) |
y = sin2 x ; |
|
2) |
y = |
1 + cos x ; |
|
3) |
y = x + sin x ; |
||
|
|
sin x |
|
|
|
x2 |
|
|
|
|
4) |
y = |
; |
5) |
y = |
1 − cos x |
; |
6) |
y =1 + sin x ? |
||
cos2 x |
|
1 −sin2 x |
||||||||
293. Розбийте даний відрізок на два проміжки так, щоб на одному |
||||||||||
з них функція y = sin x спадала, а на другому — зростала: |
||||||||||
1) |
π;2π ; |
|
2) |
−π; π ; |
|
3) − π; 3π . |
||||
2 2 2 2
294.Розбийте даний відрізок на два проміжки так, щоб на одному з них функція у = cos х набувала невід’ємних значень, а на другому — недодатних:
1) [0; π ]; |
2) |
|
π |
; |
3π |
; |
3) |
π |
|
||
− |
2 |
2 |
|
|
2 |
;2π . |
|||||
|
|
|
|
|
|
|
|
|
|||
19*

292 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 3. |
Тригонометричні Функції |
|||||||||||||||||
295. Знайдіть проміжки зростання і спадання функції: |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
1°) y = 2cos x; |
|
|
π |
|
|
|
2°) y = sin x – 3; |
π |
|
|
|
|
|
|
|||||||||||||||||||
|
3) |
|
|
|
|
|
|
3x − |
|
|
|
4) |
y =1 |
|
|
|
|
2x + |
; |
|
|
|
|
|
||||||||||
|
y = 2cos |
4 |
; |
|
|
−sin |
3 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5) |
|
|
|
|
|
|
|
|
2x − |
π |
; |
|
6) |
y =1 |
|
|
|
|
2x − |
π |
|
|
|
|
|
|
|||||||
|
y = 0,5sin |
|
|
+ cos |
3 |
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
296. |
Порівняйте числа: |
|
|
2°) sin 220° і sin 260°; |
|
|
|
|
|
|||||||||||||||||||||||||
|
1°) sin 37° і sin 86°; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
3°) cos 200° і cos 230°; |
|
4) sin |
|
− |
π |
і |
sin |
|
− |
|
|
π |
|
; |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
10 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
||||||
|
5*) cos |
|
− |
π |
|
і sin |
; |
6) sin(–3) і sin(–2); |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
||||||||
|
7) cos |
|
π |
|
і sin |
π |
; |
|
|
|
|
8*) cos |
|
|
π |
|
і sin |
. |
|
|
|
|
||||||||||||
|
|
7 |
|
7 |
|
|
|
|
− |
8 |
|
|
8 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
297. Знайдіть множину значень функції: |
|
|
|
|
– 1; 4) у = cos2х; |
|||||||||||||||||||||||||||||
|
1°) у = sin 3x; |
|
2°) |
у = 3sin |
х; 3°) y = 3cos x |
|||||||||||||||||||||||||||||
|
5) |
у = |
1 |
sin |
2 |
x −1 ; |
6) y = |
|
|
π |
; 7) y = 3cos2x |
− |
π |
. |
||||||||||||||||||||
|
2 |
|
3sin 2x − |
6 |
|
6 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
298. |
Побудуйте графік функції: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
l°) y = 2cosx; |
|
|
|
|
|
|
2°) y = sin3x; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3) |
y = cos x −1 ; |
|
|
|
|
|
4*) |
y = 3sin x − π . |
|
|
|
|
|
|
|||||||||||||||||||
3 3
299.Побудуйте графік залежності моментів заходу Сонця на перше число місяця в залежності від місяця, взявши за вісь абсцис середній час заходу Сонця — 18 годин, з’єднайте отримані точки плавною неперервною лінією (ці дані можна взяти з відривних календарів за різні роки або знайти в Інтернеті).
1)Чи є ця залежність функціональною?
2)Графік якої функції вам нагадує побудований графік?
3)Чим ви пояснюєте таку схожість?
4)Як можна уточнити побудований графік?
5)Чим ви пояснюєте відмінності побудованого графіка від графіка відомої вам функції?
6)Надайте змістовну інтерпретацію області визначення, множині значень, проміжкам монотонності, нулям, найбіль-2

Властивості і графіки тригонометричних функцій |
293 |
шому і найменшому значенням, точкам екстремуму, періо- |
|
дичності функції, графік якої побудовано. |
|
300. Знайдіть область визначення функції: |
|
1°) y = tg3x; 2°) y = tg x + π ; 3) y = 1 ; 4) y = |
1 . |
4 ctgx tgx +1
301.Які з функцій є парними, які — непарними, а які — ні парними, ані непарними:
1°) y = tgx cos2x; 2°) y = tg x + ctg x ; 3°) у = tg 2x sin х;
4°) |
y = sin x + tgx ; |
5) y = ctgx + cosx; |
6) |
y = x + sin x ? |
|
|
|||||||||||
|
|
x2 |
|
|
|
|
|
|
tg3x |
|
|
|
|
||||
302. Порівняйте числа: |
|
|
2) tg π |
|
|
|
|
4π |
|
|
|
||||||
1) tg (–80°) і tg (–50°); |
|
і tg |
; |
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
π |
5 |
|
|
π |
|
|
3) tg 1 і tg l,6; |
|
4) tg (–2) і tg (–3); |
5) ctg |
|
|
|
і ctg |
; |
|||||||||
|
− |
8 |
|
9 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6) ctg 95° і ctg 117°; |
7) ctg 2 і ctg 3; |
8) tg π |
і ctg π . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
303. Вкажіть проміжки зростання і спадання функції: |
|
|
|
|
|
||||||||||||
1°) y = ctg 2x; |
|
2°) y = ctg x – 1; |
3) y = 2tg x; |
|
|
|
|
||||||||||
4) |
|
+ |
π |
|
5*) у = tg2 x; |
6*) y = ctg2 x; |
|
|
|||||||||
y = tg x |
4 |
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7*) |
x |
− |
π |
|
8*) y = 2 |
|
x |
+ |
π |
|
|
|
|
|
|||
y = tg |
2 |
; |
|
+ ctg |
|
. |
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
3 |
|
4 |
|
|
|
|
|
|||
304. Знайдіть множину значень функції: |
|
|
|
|
|
|
|
|
|
|
|
||||||
1°) y = tg(x |
+ 1); |
|
2°) y = сtgx – 1; |
|
|
|
|
|
|
|
|
|
|||||
3) y = ctgx,0 < x < π; |
4) y = tg2x ; |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4 |
|
y = ctg3x ; |
7) |
y = −ctg2x . |
|
|
|||||||
5) y = tg x ctg x; |
6) |
|
|
||||||||||||||
305. Вкажіть найбільше і найменше значення функції: |
|
|
|
|
|||||||||||||
1°) y = tgx, − |
π |
≤ x ≤ |
π; |
2) y = ctg x , |
π ≤ x ≤ |
2π |
; |
|
|
||||||||
4 |
|
|
|
||||||||||||||
|
|
|
|
4 |
|
2 |
3 |
|
|
|
|
3 |
|
|
|
|
|
3) y = sinx + tgx, 0 ≤ x ≤ 4π.

294 |
|
|
|
|
|
|
|
|
Розділ 3. Тригонометричні Функції |
||||
306. Побудуйте графік функції: |
|
|
|
|
|
||||||||
1°) |
y = tgx, x |
|
− |
3π |
;− |
π |
|
; |
2°) y = ctgx, x (−π; 0); |
||||
|
2 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
3°) у = ctgx – l; |
|
|
|
|
|
|
|
4°) |
|
π |
|
|
|
|
|
|
|
|
|
|
y = tg x + |
; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
tgx при x ≤ π , |
|
||
5) |
y = tg x ; |
|
|
|
|
|
|
|
6*) |
|
4 |
|
|
|
|
|
|
|
|
|
y = |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
π |
. |
|
|
|
|
|
|
|
|
|
|
ctgx при x > |
4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
307°. Знайдіть амплітуду, період і початкову фазу гармонічного |
||||||||||||
коливання, яке задано формулою: |
|
|
|
|
|
|
|
|||||
l) |
|
π |
|
1 |
|
π |
|
t |
|
|
|
|
y = 3sin 2t + |
; |
2) y = |
2 |
sin πt + |
|
;3) |
y = 2sin |
|
+1 |
|
; |
|
|
||||||||||||
4) |
|
3 |
|
|
4 |
|
2 |
|
|
|
||
у = 3 sin 4t; |
|
5) y = sin (t – 1). |
|
|
|
|
|
|
|
|||
308°. Дано закон, за яким змінюється координата (яка вимірюєть-
ся в сантиметрах) тіла, що рухається. Знайдіть амплітуду,
період, кругову частоту коливання. Обчисліть координату |
|||
тіла в момент часу t0, якщо: |
|||
1) x(t) = 2,5cos3πt,t = 1 c; |
|||
|
0 |
9 |
|
2) x(t) = 7cos 4πt + |
π |
||
,t = 2,5 c; |
|||
|
|
0 |
|
|
4 |
|
|
3) x(t) = 2cos2πt,t0 = 0,25 c;
4) x(t) =1,5cos πt + π ,t = 3,5 c.
3 6 0
309.Дано закон, за яким змінюється з часом сила змінного струму: I(t) = 5sin10πt, I — сила струму, A; t — час, с.
1°) Знайдіть амплітуду, період, кругову частоту коливань сили струму.
2°) Чому дорівнює сила струму в момент часу t = 0,05 c?
3)В які моменти часу сила струму набуває найбільшого значення?
Дано закон, за яким змінюється з часом напруга:
—напруга, В; t — час, с.310. U(t) = 220cos60πt,
1°) Знайдіть амплітуду, період, частоту коливань напруги. 2°) Чому дорівнює напруга у момент часу t = 0,5 c?

Властивості і графіки тригонометричних функцій |
295 |
3) В які моменти часу напруга набуває найбільшого зна- |
|
чення? |
|
311. Точка виконує гармонічне коливання за законом:
|
π |
y = 3sin 2t + |
. |
|
3 |
1) Знайдіть амплітуду, період і початкову фазу цього коли- |
|
вання. |
|
2) Вкажіть, які перетворення слід виконати над синусоїдою |
|
у = sin t, щоб одержати графік даного коливання. |
|
3) Побудуйте схематично графік гармонічного коливання. |
|
312. Ордината точки, що обертається по колу, виконує гармоніч-
не коливання за законом: |
|
|
3t − |
π |
|
|
|
y = 2sin |
2 |
. Знайдіть момен- |
|||||
|
|
|
|
|
|
|
|
ти часу, в які точка розташована у крайньому положенні: |
|||||||
1) |
верхньому; |
2) |
лівому; |
|
|
|
|
3) |
нижньому; |
4) |
правому. |
|
|||
313. Напишіть рівняння гармонічного коливання, якщо: |
π; |
||||||
1) амплітуда дорівнює 1, період |
0,2 с, початкова фаза |
||||||
2) |
|
|
|
|
|
|
6 |
за 1 хв здійснюється 180 коливань з амплітудою 7 см, а |
|||||||
початкова фаза коливань дорівнює |
π . |
|
|
|
|||
|
|
|
|
2 |
|
|
|
Вправи для повторення
314.Який знак має скалярний добуток векторів, якщо кут між ними є: 1) гострим; 2) тупим? Чи справджуються обернені твердження?
315. Обчисліть скалярний добуток векторів a і b , якщо a = 2, b = 3 і кут між ними дорівнює: 1) 60°; 2) 135°; 3) 90°;
4)0°; 5) 180°.
316.Чому дорівнює скалярний добуток векторів: 1) (а; 0) і (b; 0);
2)(а; 0) і (0; b); 3) (а; b) і (a; b); 4) (а; b) і (–a; – b)?
317.Дано вектори a = (1; 2),b = (−2; 3). Обчисліть:
1) |
2a · b ; |
2) a · (–3b ); |
3) |
|
− |
1 |
|
1 |
|
; |
|
|
2 |
a |
|
3 |
b |
||||||
|
|
|
|
|
|
|
|
|
|
||
4) b · (a + b ); |
5) (a + b )2; |
6) (a – b )2; |
|
|
|
||||||
7) (a + b ) · (a – b ). |
|
|
|
|
|
|
|
|
|
||

296 |
|
|
Розділ 3. |
Тригонометричні Функції |
||
|
|
|
Підсумок |
|
|
|
|
|
|
Основне поняття |
|
|
|
Означення |
Геометрична |
Застосування |
||||
ілюстрація |
||||||
|
|
|
|
|
||
Функція у = f(х) на- |
|
Періодичніфунк- |
||||
зивається періодич- |
|
ціїописуютьрізні |
||||
ною, |
якщо |
існує |
|
ситуації |
(астро- |
|
таке |
число |
T ≠ 0 , |
|
номічні |
явища, |
|
що область |
визна- |
|
життєдіяльність |
|||
чення |
функції ра- |
|
організму,гармо- |
|||
зом з кожною точ- |
|
нічні коливання |
||||
кою х містить точки |
|
тощо), які періо- |
||||
х ± Т |
і при цьому |
|
дично |
повторю- |
||
виконується |
рів- |
|
ються. |
|
||
ність f(х ± Т) = f(x). |
|
|
|
|||
Число Т називаєть- |
|
|
|
|||
сяперіодомфункції. |
|
|
|
|||
|
|
|
Головні твердження |
|
|
|
Словесне формулювання
Функції у = sinх
і у = cos х — пе-
ріодичні з найменшим додатним періодом
2π.
Функція у = tg х періодична з найменшим додатним періодом π.
Запис за допо- |
Графічна ілюстрація, |
|
могою формул, |
||
коментарі, пояснення |
||
пояснення |
|
sin(x + 2π) = sin x cos(x + 2π) = cos x
tg(x + π) = tgx

Властивості і графіки тригонометричних функцій |
297 |
|||||||||||||||
Словесне фор- |
Запис за допо- |
|
|
|
Графічна ілюстрація, |
|||||||||||
могою формул, |
|
|
|
|||||||||||||
мулювання |
|
|
|
|
коментарі, пояснення |
|||||||||||
|
|
|
|
|
пояснення |
|
|
|
|
|
|
|
|
|
|
|
Множиною зна- |
E(y) = [–1; 1] |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
чень |
|
функцій |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
у = sin |
х і у |
= |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= cos |
х |
є відрізок |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
[–1; 1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Функція |
у |
= |
sin (–х) = –sin х, Графік функції у = sin х си- |
|||||||||||||
= sin |
х |
— непар- |
cos(–х) = cosх |
метричний відносно початку |
||||||||||||
на, |
а |
функція |
|
координат, графік |
функції |
|||||||||||
у = cos х |
— пар- |
|
у = cos х симетричний віднос- |
|||||||||||||
на |
|
|
|
|
|
но осі ординат |
|
|
||||||||
Функція у = tg х |
Функція у = tg х |
|
|
|
|
|
|
|
|
|
|
|
||||
неперервна при |
має розрив у точ- |
|
|
|
|
|
|
|
|
|
|
|
||||
всіх |
значеннях |
ках, де знамен- |
|
|
|
|
|
|
|
|
|
|
|
|||
аргументу, крім |
ник виразу tg х = |
|
|
|
|
|
|
|
|
|
|
|
||||
x = π |
+ kπ, k Z . |
= sin x перетво- |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рюється в нуль. |
|
|
|
|
|
|
|
|
|
|
|
Множиною зна- |
Е(у) = R |
|
|
|
|
|
|
|
|
|
|
|
||||
чень функції у |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= tg |
х |
є множи- |
|
|
|
|
|
|
|
|
|
|
|
|
||
на всіх дійсних |
|
|
|
|
|
|
|
|
|
|
|
|
||||
чисел. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функція у = |
tg (–х) = –tg х Графік функції у = tg х си- |
= tg х — непар- |
метричний відносно початку |
на. |
координат. |
