Добавил:

quantum researchgate.net Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский государственный экологический университет

Предмет:

Аналитическая геометрия

Файл:

978-966-10-1272-0_Математика. Підручник для 10 класу. загальноосвітніх навчальних закладів. Рівень стандарту.pdf

Скачиваний:

981

Добавлен:

24.03.2018

Размер:

8.73 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2615 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

§14. основні співвідношення між тригонометричними функціями

У даному параграфі встановлюються співвідношення між тригонометричними функціями, які дозволяють за значенням однієї з функцій за певних умов знаходити значення всіх інших. Ðозглядаються також формули, які зводять обчислення значень тригонометричних функцій у довільній точці до обчислення їхніх значень для аргу-

менту з проміжку 0;	π	.
	2

1. Основна тригонометрична тотожність та наслідки з неї

Знайдемо зв’язок між сину- сом і косинусом того само- го аргументу. Нехай Рt(х(t);

у(t)) — точка тригонометричного кола, 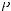яка відповідає числу t (рис. 294). Тоді, за означенням синуса і косинуса, маємо такі рівності:

х(t) = cos t, y(t) = sin t.

Оскільки точка Рt належить тригономе-

тричному колу, то її координати задовольняють рівняння кола х2 + у2 = 1. Отже, для довільного t справджується рівність:

cos2t + sin2t = 1.

Ця рівність називається основною тригонометричною то-

тожністю.

До основних співвідношень між тригонометричними функціями одного аргументу відносять також рівності:

tgt = sincostt ; ctgt = sincostt .

252 Розділ 3. Тригонометричні Функції

З наведених вище рівностей випливають інші залежності між
тригонометричними функціями одного і того самого аргументу:
	2		1			2	1
tgt ctgt =1,	1 + tg	t =		,		1 + ctg t =			.
			cos2 t					sin2 t
Перша з них є простим наслідком означень тангенса і котан-
генса. Доведемо другу. Маємо:					2	sin2 t	cos2 t + sin2 t
			1 + tg			t =1 + cos2 t =		cos2 t		=

= cos12 t . Третє співвідношення виводиться аналогічно. Рекомендуємо зробити це самостійно.

!Наведені співвідношення дозволяють за значенням однієї з тригонометричних функцій числа t обчислювати квадрати значень інших. Наприклад, якщо cost = 13 , то

sin2 t =1 − cos2 t =1 − 19 = 89 . Для знаходження самих зна-

чень потрібна додаткова інформація, яка б надавала можливість встановлювати їхні знаки.

У попередньому параграфі розглядались приклади, де доводилось за означеннями тригонометричних функцій визначати знаки їхніх значень. Узагальнимо ці міркування, з’ясувавши, при яких значеннях аргументу тригонометричні функції набувають додатних значень, а при яких — від’ємних.

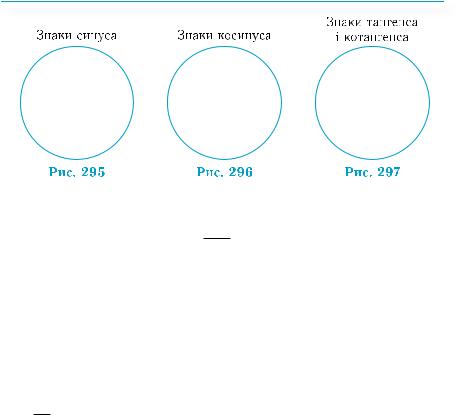
Синус числа t — це ордината точки Pt (див. рис. 294). Додатни-

ми є ординати тих точок, які розміщені над віссю абсцис, тобто знаходяться у першій чи у другій чверті. Якщо точка Pt розташо-

вана під віссю абсцис, тобто в третій або у четвертій чверті, то її ордината є від’ємною (рис. 295).

Властив³сть 1. Синус набуває додатних значень у пер-

шій і другій чвертях, а від’ємних — у третій і четвертій.

Далі міркуємо аналогічно. Косинус числа t — це абсциса точки Pt . Додатними є абсциси тих точок, які розміщені правіше від осі

ординат, тобто знаходяться у першій чи у четвертій чверті. Якщо точка Pt розташована лівіше від осі ординат, тобто в другій або у

третій чверті, то її абсциса є від’ємною (рис. 296).

Основні співвідношення між тригонометричними функціями

253

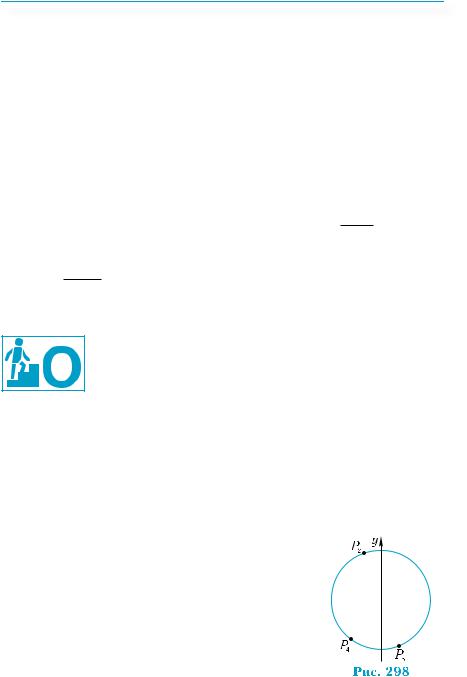
Властив³сть 2. Косинус набуває додатних значень у пер-

шій і четвертій чвертях, а від’ємних — у другій і третій.

Згідно з означенням, tgt = sincostt , ctgt = sincostt , тому tg t і ctg t набувають додатних значень, якщо sin t і cos t мають однакові знаки. Відповідно, tg t і ctg t набувають від’ємних значень, якщо sin t і cos t мають різні знаки (рис. 297).

Властив³сть 3. Тангенс і котангенс набувають додатних

значень у першій і третій чвертях, а від’ємних — у другій і четвертій.

Ïðèê ëàä 1. Визначити знаки чисел: 1) cos 230°; 2) sin 79π ;

3)tg 95π .

1) Визначимо, в якій чверті знаходиться точка тригонометричного кола, яка визначає положення кута 230°. Маємо: 180° < < 230° < 270°. Тому зазначена точка лежить у третій чверті. Косинус у третій чверті набуває від’ємних значень. Тому cos 230° < 0.

2) Визначимо спочатку, в якій чверті знаходиться точка тригономе-

тричного кола, що відповідає числу 7π . Оскільки π <							7π < π, то числу
				9	2		9
7π	відповідаєточка,яказнаходитьсяудругійчверті.Тому sin 7π							>0.
9							9
	3)Оскільки 3π <			9π < 2π,тоточка P9π розміщенаучетвертійчвер-
	2			5	5
ті і tg		9π	< 0.
ті і tg			< 0.
	5
	Відповідь. 1) cos 230° < 0; 2) sin 7π				> 0 ; 3) tg	9π	< 0.
	Відповідь. 1) cos 230° < 0; 2) sin 7π				> 0 ; 3) tg		< 0.
				9	5

254	Розділ 3. Тригонометричні Функції

Приклад 2. Відомо, що cos t = – 0,6 і π	< t < π . Знайти sin t, tg t.
2			= 1 – cos2t =
 З тотожності sin2t + cos2t = 1 знаходимо: sin2t			= 1 – cos2t =
=1 −(−0,6)2 = 0,64 . Оскільки π < t < π ,	то	точка Pt	розміщена
2		tgt = sint = − 4 .
у другій чверті і sint > 0 . Тому sint = 0,8;		tgt = sint = − 4 .
		cost	3

Відповідь. 0,8; − 4 .
3
Ïðèê ëàä 3 . Спростити вираз cos2 α −(ctg2α +1)sin2 α.
 Застосовуючи послідовно рівність	1 + ctg	2	1	і основну
	1 + ctg		t = sin2 t

тригонометричну тотожність, матимемо: cos2 α −(ctg2α +1)sin2 α =

= cos2 α − sin12 α sin2 α = cos2 α −1 = −sin2 α.

Відповідь. −sin2 α.

При перетворенні тригонометричних виразів, як і алгебраїчних, області їхнього визначення можуть змінюватись. Так, у прикладі 3 даний вираз визначений при всіх дійсних значеннях α, окрім α = πп,

п Z. Спрощений вираз визначений при всіх дійсних значеннях

α. Щоб не ускладнювати запис, зазвичай домовляються, що рів-

ність даного виразу і спрощеного, отриманого за допомогою пере-

творень, справджується для всіх значень змінних, при яких визначені обидва вирази.

Розглянемо складніші приклади на застосування основних тригонометричних співвідношень.

Ïðèê ëàä 4. Визначити знаки чисел: sin2;

cos3; tg4; ctg5.

 Відмітимо на тригонометричному колі точки Р2, Р3, Р4, Р5 (рис. 298). Враховуючи, що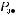

sin 2 — це ордината точки P2 , дійдемо висно-

вку, що sin 2 > 0. Оскільки cos 3 – це абсциса точки P3 , то cos 3 < 0. Знаки tg4 і ctg 5 визна-

чимо, користуючись означеннями тангенса

Основні співвідношення між тригонометричними функціями				255
і котангенса: tg4 = sin		4 > 0, бо sin 4 < 0, cos 4 < 0,	ctg 5 = cos5	< 0 ,
	cos	4	sin5
бо sin 5 < 0, cos 4 > 0.
Відповідь.	sin 2 >0; cos 3 < 0; tg 4 > 0; ctg 5 < 0.
Ïðèê ëàä 5 .	Довести, що

sin3 α(1 − ctgα) − cos3 α(1 − tgα) = sin α − cosα .

 Скориставшись означеннями tgα і ctgα та основною триго-
нометричною тотожністю, одержимо:						cos α			sin α
sin	3	3	α(1 − tgα) = sin	3		cos α	3		sin α	=
sin		α(1 − ctgα) − cos	α(1 − tgα) = sin		α 1 −		− cos	α 1 −		=
						sin α			cosα

= sin

sin α − cosα

− cos

cosα −sin α

= sin

α(sin α − cosα)−

sin α

cosα

– cos2 α(cosα −sin α) = (sin α − cosα)(sin2 α + cos2 α)= sin α − cosα.

Зверніть увагу на те, що у прикладі 5 вирази, що стоять у лівій і правій частинах рівності, мають різні області визначення, але їхні значення на спільній частині областей визначення співпадають.

 Контрольні запитання

1°. Яке рівняння задовольняють координати всіх точок тригонометричного кола?

2°. Чи можуть синус і косинус одного й того самого аргументу дорівнювати відповідно: а) 0 і 0; б) 1 і 0; в) 1 і –1; г) 0,6 і 0,8; ґ) 0,5

і 0,5?

3. Чи правильно, що cos t = 35 , якщо sint = 45 ?

4. Чи можуть тангенс і котангенс одного й того самого аргументу

дорівнювати відповідно: а°) 1 і 0; б°) 1 і 1; в°) 1 і –1; г) 3	і	1	;
		3

ґ) 2 + 3 і 2 − 3 ; д) 1 + 2 і 1 − 2 ?

5.Для яких точок Pt тригонометричного кола мають різні знaки:

а) sint і cos t; б) sin t і tg t?

6.Де розміщена точка Рt на тригонометричному колі, якщо:

а°) sin t > 0; б°) tg t < 0; в) cos 2t < 0; г) sin t cos t < 0; ґ) |sin t| = –sin t?

256	Розділ 3. Тригонометричні Функції

			2. Формули зведення
			Існують формули, які зводять обчислення значень
			Існують формули, які зводять обчислення значень
			тригонометричних функцій для довільного аргу-
			менту до обчислення їхніх значень на проміжку
	π	. Ці формули називають формулами зведення.
0;	2	. Ці формули називають формулами зведення.
	2

Формули зведення ґрунтуються на означеннях тригонометрич-

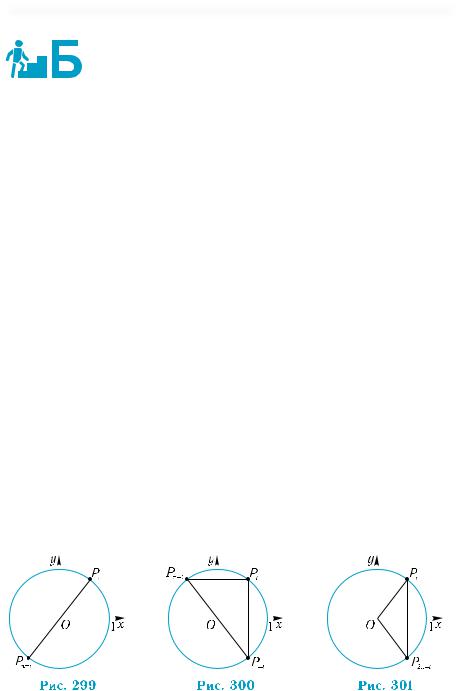
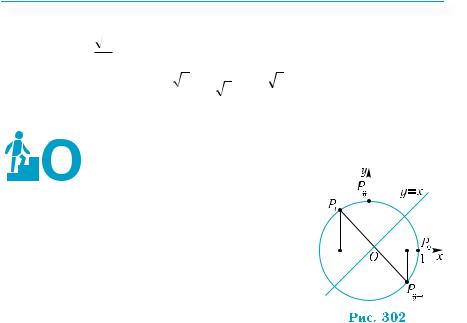
них функцій і властивостях геометричних перетворень – поворотів. Розглянемо на тригонометричному колі точку Pt (рис. 299).

Точку Pπ+t можна одержати з точки Pt за допомогою повороту на кут π. Тому точки Pt і Pπ+t симетричні відносно початку коорди-

нат. Їхні координати — протилежні числа. Отже, мають місце наступні формули:

cos(π +t) = −cost; sin(π +t) = −sint .

Точки Pt , Pπ−t симетричні відносно осі ординат (рис. 300). Вони

мають однакові ординати і протилежні абсциси. Це випливає з того, що точки Pt і P−t симетричні відносно осі абсцис, а точки P−t

і Pπ−t симетричні відносно початку координат. Тому справджуються наступні формули:

	cos(π −t) = −cost;		sin(π −t) = sint .
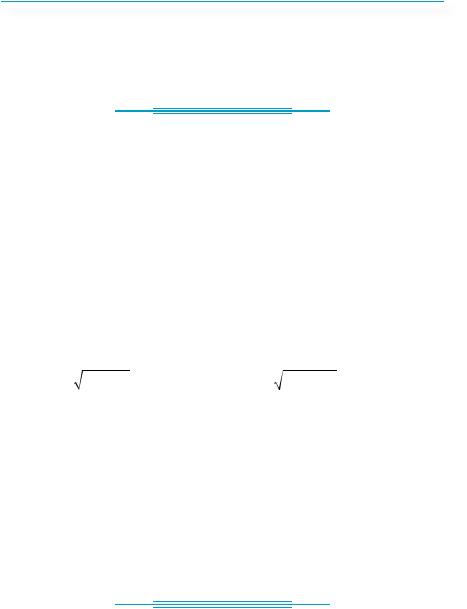
Точки P−t	і P2π−t	збігаються (2π — повний оберт!) (рис. 301),
тому точки Pt	і P2π−t	симетричні відносно осі абсцис, у них одна-
кові абсциси і протилежні ординати. Відповідні формули мають
такий вигляд:			sin(2π −t) = −sint .
	cos(2π −t) = cost;		sin(2π −t) = −sint .
Оскільки точки Pt		і P2π+t збігаються, то справджуються наступ-
ні формули:			sin(2π +t) = sint .
	cos(2π +t) = cost;		sin(2π +t) = sint .

Основні співвідношення між тригонометричними функціями

257

!Головною особливістю наведеної групи формул є те, що вони стосуються лише однієї тригонометричної функції. Існує ще одна група формул зведення для синуса і косинуса. Вона відрізняється тим, що в кожній формулі містяться обидві тригонометричні функції.

Формулизведеннядлятангенсаікотангенсавипливаютьізозна-

чень цих функцій і відповідних формул для синуса і косинуса.

Наприклад, tg (π +t) =

sin (π +t)

= −sint = tgt;

cos(π +t)

−cost

cos

−sint

= −tgt.

ctg

cost

sin

Узагальнено формули зведення подані у таблиці 29.

Таблиця 29

Аргумент

3π

−t

π −t

π +t

−t

2π −t 2π +t

Функція

sin

cos t

sin t

–sin t

–cos t

–sin t

sin t

cos

sin t

–sin t

–cos t

–sin t

sin t

cos t

ctg t

–ctg t

–tg t

tg t

сtg t

–ctg t

–tg t

tg t

ctg

tg t

–tg t

–ctg t

сtg t

tg t

–tg t

–ctg t

ctg t

= cost,

= sint;

sin

−t

cos

−t

= cost,

cos

= −sint;

sin

3π

−t

= −cost,

cos

3π

= −sint;

sin

−t

3π

= −cost,

cos

3π

= sint.

sin

Обґрунтуємо наведені формули пізніше.

Аналізуючи таблицю, можна сформулювати так зване мнемонічне правило, яке дозволяє краще запам’ятати формули зведення.

17 Математика, 10 кл.

258	Розділ 3. Тригонометричні Функції

1) У формулі зведення функція не змінюється, якщо до аргументу додавати ±π або ж ±2π , і змінюється (синус на

косинус, тангенс на котангенс, косинус на синус, котангенс на тангенс), якщо додавати числа ± 2π чи ±32π .

2)Одержана функція у правій частині рівності береться

зтим самим знаком, який має початкова функція, якщо

вважати, що 0	< t <	π
		2 .
Ïðèê ëàä 6 .	Знайти cos(270° – α).

 Насамперед, помічаємо, що вираз містить кут 270° або 2π рад.

Тому функція змінюється, і у правій частині рівності має стояти sinα. Щоб визначити знак перед sinα, припускаємо, що кут α — гострий. Тоді точка P270°−α лежить у третій чверті тригонометрич-

ного кола. Але косинус у третій чверті — від’ємний. Тому перед sinα слід поставити знак «–» . Отже, cos(270° – α) = –sinα.

Відповідь. –sinα.

Приклад 7. Обчислити:1) sin116π; 2) cos 54π; 3) tg 43π; 4)sin1020°.

 Для розв’язання перших трьох завдань подамо число, яке стоїть під знаком тригонометричної функції, у вигляді суми або

різниці чисел π або 2π і деякого числа, яке менше від																			π	, і застосу-
																			2
ємо відповідну формулу зведення. Необхідні пояснення наведені
при розв’язанні прикладу 6:
1)	sin		11π			= sin				π	= −sin			π	= −		1	;
1)	sin		6			= sin	2π −				= −sin			6	= −		2	;
			6							6				6			2
2)			5π						π				π			2		;
	cos				= cos		π +			= −cos				= −
	cos		4		= cos		π +		4	= −cos			4	= −		2
			4						4				4			2
3)	tg	4π						π			π	=	3 .
3)	tg		3	= tg π +				3	= tg		3	=	3 .
			3					3			3

В останньому завданні виділимо з наведеного кута обертання

повні оберти, міри яких кратні 360°, їх можна відкинути. Далі застосовуємо формулу зведення.

Основні співвідношення між тригонометричними функціями

259

4)sin 1020° = sin(2 · 360° + 300°) = sin 300° = sin(360° – 60°) =

=–sin 60° = − 23 .

Відповідь. 1) − 1

; 2) −

; 3)

3; 4) −

Тепер обґрунтуємо формули, в яких до аргументу

додаються

π або

3π .

і Pπ

Візьмемо дві точки P0

(рис. 302). Вони симетричні одна одній від2-

носно бісектриси першого і третього коорди-

натних кутів. Щоб побудувати точку Pt ,

по-

трібно рухатись

по

колу від точки P0

на

відстань

у певному напрямі. Щоб побуду-

вати точку

Pπ

, треба на таку саму відстань

−t

рухатись по колу від точки Pπ , але у протилежному напрямі. При

цьому точки

Pπ−t

при

будь-якому t залишатимуться

симетричними відносно зазначеної прямої (у = х).

Звідси випливає, що ордината першої точки збігається з абсци-

сою другої, а її абсциса — з ординатою другої, тобто

= sint .

sin

−t

= cost; cos

−t

Усі інші формули обґрунтовуються за допомогою цих і раніше

отриманих формул:

−t

sin

= sin

π −

= sin

= cost;

= −sint;

cos

= −cos π −

= −cos

−t

3π

−t

= sin

π +

= −sin

= −cost;

sin

−t

3π

−t

π +

= −cos

= −sint.

cos

= cos

−t

17*

260							Розділ 3. Тригонометричні Функції
3π				π			π			= −cost;
sin	2	+t	= sin	π +	2	+t	= −sin	2	+t	= −cost;
	2				2			2
3π				π			π			= sint.
cos	2	+t	= cos	π +	2	+t	= −cos	2	+t	= sint.
	2				2			2

Для тангенса і котангенса кількість формул зведення можна зменшити. Справа в тім, що тангенс і котангенс довільного аргу-

менту можна звести до цих функцій аргументу з проміжку [0; π].

Справді, кожній точці на лінії тангенсів чи лінії котангенсів відповідає безліч чисел t + πn, n Z, тому тангенс і котангенс для t + πn при всіх n Z набувають того самого значення:

tg (t + πn) = tg t, ctg (t + πn) = ctg t.

Послуговуючись цим висновком, для переходу до тангенса чи

котангенса

гострого кута

достатньо

знати

формули тангенса

і котангенса для π ±t, π −t (90°±t,180°−t).

17π;

11π

Ïðèê ëàä

8 . Обчислити:

1) tg

2) ctg

 Виділимо з аргументу цілу кількість значень π.

17π

5π

= tg 2π +

= tg

= tg π −

= −tg

= −

;

ctg

11π

3π

= ctg

= −ctg

= −1.

= ctg 2π +

= ctg

π −

Відповідь. −

;

–1.

 Контрольні запитання

1.Як розміщені на тригонометричному колі одна відносно дру-

	гої точки: а°)	Pπ+t і Pt ; б°) Pπ−t			і Pt ; в) Pt і Pπ−t ; г) Pt	і P	3π	−t ?
					2	2
2°.	Яка точка симетрична точці				Pt тригонометричного кола від-
	носно: а) початку координат; б) осі ординат; в) осі абсцис?
3.	Які координати має точка тригонометричного кола, симетрич-
	3	;	4
	на точці P	;	5	відносно: а°) початку координат; б°) осі ор-
	5		5
	динат; в°) осі абсцис; г) прямої у = х; ґ) прямої у = –х?

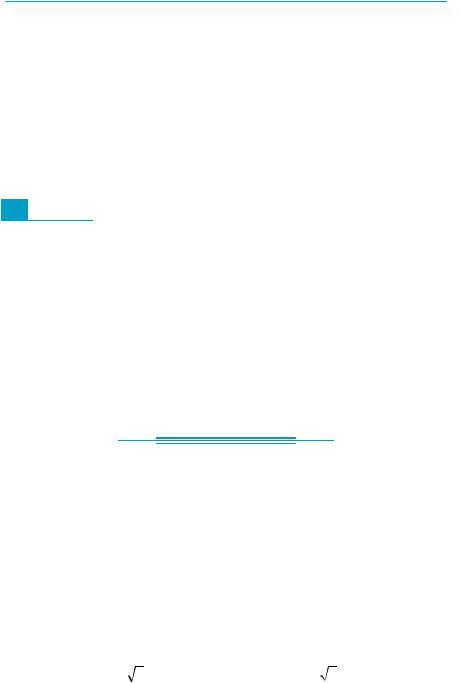
Основні співвідношення між тригонометричними функціями

261

4.Як можна представити кут 112°, щоб скориставшись формулами зведення обчислити cos 112°?

5.Чому дорівнює вираз:

а) sin (π +1)+ sin1; б) sin (π +1)+ sin (π −1); в) cos π +1 + sin1?

6.Чи правильним є твердження, що косинус суми двох кутів трикутника дорівнює косинусу третього кута?

7.Чому дорівнює тангенс тупого кута паралелограма, якщо тан- генс гострого кута дорівнює 32 ?

Задачі

259.

Визначте знак виразу:

3°) sin 4πcos 9πtg 2π

1°) sin 65°;

2°) tg 147° sin 269°;

;

4) sin(−2) cos2 tg(−3) ;

5*) sin

3πtg 7πcost .

260.

Нехай 0 < α <

. Визначте знак виразу:

;

+ α

3) sin (2α − π);

1°) sin

− α

2°) cos

;

4) tg (α − π);

5) cos(π − α);

2π −

6) ctg

261.Обчисліть значення кожної з тригонометричних функцій, якщо:

1°) sint = −0,8;				3π	< t < 2π ;	2°) cost = −	12	; π < t <	3π	;
1°) sint = −0,8;				2	< t < 2π ;	2°) cost = −	13	; π < t <	2	;
				2			13		2
3) tgt = −2,4;			π	< t < π ;		4) ctgt = 3; 0 < t < π ;
			2	< t < 3π ;			5	2
5°) sint =0,6;			π			6°) cost = −	5	; π < t < 2π .
5°) sint =0,6;			2			6°) cost = −	13	; π < t < 2π .
			2	2			13
262. Знайдіть координати точки						Pt на тригонометричному колі,
якщо:
1) ctgt = −	5	;				2) tgt = −4 ;
1) ctgt = −		;				2) tgt = −4 ;
12						3
3*) ctgt = 2 +			3;			4*) tgt =1 +	2 .

262
263. Обчисліть:
1)		tg α	, якщо sin α = −	2
1)	1 − cosα		, якщо sin α = −	3
	1 − cosα			3
2)		ctgα	, якщо cosα = −	3
2)	1 + sin α		, якщо cosα = −	4
	1 + sin α			4

Розділ 3. Тригонометричні Функції

іctg α > 0;

іctg α < 0.

264.

Спростіть вираз:

1°)

sin2 α −1

cos2 α −1

1 − cos2 α

;

1 −sin2 α;

3°)

cosαtgα −sin α ;

4°)

cosα −sin αctg α;

5°)

cos2 α + ctg2α + sin2 α ;

6°)

cos2 α + tg2α + sin2 α ;

;

8) 1 + tg

;

7) 1 + ctg

α +

cos2 α

sin2 α

9) 1 + ctg2α ;

10)

1 + tg2α

;

1 + ctg2 α

1 + tg2α

11) sin2 α −sin4 α + cos4 α ;

12) cos2

α − cos4 α + sin4 α ;

13) (tg α + ctg α)(1 + cosα)(1 − cosα)

;

14)

(tg α + ctg α)(1 + sin α)(1 −sin α) ;

15*)

tgα

;

16*)

ctg α

1 + tg2

1 + ctg2α

265.

Доведіть тотожність:

1°)

;

sin2

cos2

sin2 α cos2

2) ctg2α − tg2α = cos2 α −sin2 α;

sin2 α cos2 α

3°) cos4 α −sin4 α =1 −2sin2 α;

4°) sin4 α − cos4 α =1 −2cos2 α;

5) tg2α −sin2 α = tg2α sin2 α;

6) ctg2α − cos2 α = ctg2α cos2 α;

7)cos2 α + 2sin2 α + sin2 αtg2α =

;

cos2 α

8) sin2 α + 2cos2 α + cos2 αc tg2α =

sin2 α

266°. Обчисліть значення тригонометричних функцій для на-
ступних кутів:		3) 150°;	4) 210°;	5) 225°;
1) 120°;	2) 135°;
6) 240°;	7) 300°;	8) 315°;	9) 330°;	10) 390°.

Основні співвідношення між тригонометричними функціями

263

267°. Користуючись формулами зведення, обчисліть:

1) sin

19π

;

2) cos

11π

;

11π

;

4) ctg

31π

;

7π

13π

4π

7π

−

8) ctg

−

5) sin

;

6) cos

; 7)

;

268°. Обчисліть значення виразу:

1) cos 990°

– sin 780° – ctg 945°;

2) tg 1080°

– sin 855° + cos 1305°;

3) 3cos 1860°

+ sin(–1920° ) + cos(–630°);

4) cos 2850° – cos (–765°) + tg 1035°.

269. Зведіть до тригонометричних функцій додатного аргументу, меншого від π:

1)9 ; 2) cos 359π; 3) tg 3512π; 4) ctg 185π.

270.Зведіть до значення тригонометричної функції для числа зsin 28π

			π
	відрізка 0;		:
			4
	1)	sin 4π ;	2) cos 7π ;	3) tg −5π ; 4)		ctg −11π .
		3	4				6
		3	4		4		6
271.	Обчисліть:
	1)	(sin10°+ sin 20°+ sin30°)−(cos60°+ cos70°+ cos80°);
	2*) ctg 31° ctg 32° ctg 33° … ctg 57° ctg 58° ctg 59°.
272.	Обчисліть суму:
	1)	sin 0°+ sin1°+ sin 2°+...+ sin359°+ sin360°;
	2)	tg20°+ tg40°+ tg60°+...+ tg160°+ tg180°.

273. Спростіть вираз:

sin(π + α)

+ cos

+ α

+ cos(2π − α)

sin α

− α

cosα

−

;

sin(π + α)

ctg(π − α)

cos(π − α)

3π

ctg

− α

− tg(π + α) + sin

− α

;

cos(π + α)

−sin 3π − α 2 ;

264

Розділ 3. Тригонометричні Функції

3π

sin

+ α

− α

ctg(2π − α)

sin(π + α)

274. Доведіть тотожність:

= 0

sin

+ α − cos

− α

; 2)tg

+ α

= ctg

− α .

275. Косинус одного зі суміжних кутів дорівнює −1213 . Знайдіть синус другого суміжного кута.

276. Косинус одного з кутів паралелограма дорівнює −135 . Зна-

йдіть синус другого з його кутів.

277. Сума косинусів гострих кутів прямокутного трикутника дорівнює m. Знайдіть:

1) суму квадратів синусів цих кутів;

2*) добуток синусів цих кутів.

Вправи для повторення

278.Виберіть серед кутів:

1) 205°; 335°; 385°; 695°; 745°; –25°; –205°; –335° такі, синус яких дорівнює sin 25°;

	2) π; 4π; 6π; 11π; 21π; −					4π; −	9π; −	19π такі, косинус яких
	5	5	5	5	5	5	5	5
	дорівнює cos			π .
279.				5
279.	На рис. 303 зображено графік функції y = f(x), визначеної на
	множині усіх дійсних чисел. Яким буде графік функції:
	1) y = f(x – 1);				2) y = f(x + 1);				3) y = f(x – 2)?
280.	Данографікифункцій,визначенихнавідрізку[–1;0](рис.304).
	Добудуйтекожнийзних(якщоцеможливо)дографіка:1)пар-
	ної функції; 2) непарної функції.

Основні співвідношення між тригонометричними функціями

265

Підсумок

Головні твердження

Назва твердження або словесне формулювання

Основна

тригонометрична тотожність і наслідки з неї

Функція не змінюєть-

ся, якщо до аргументу t додати ±π або ж

±2π , і змінюється (си-

нус на косинус, тангенс на котангенс,

косинус на синус, ко-

тангенс на тангенс), якщо додати числа

± 2π чи ± 32π . Знак у

правій частині рівності збігається зі знаком у лівій частині, якщо t задовольняє

умову: 0 < t < 2π .

Зміст Графічна твердження ілюстрація

sin2t + cos2t = 1,


	2	1
1	+ tg t	=			,
			cos2 t
	2	1
1	+ ctg	t =
				sin2 t

sin(π +t) = −sint cos(π +t) = −cost sin(π −t) = sint cos(π −t) = −cost

π						= cost;
sin			−t
2
π						= sint
cos				−t
2
π						= cost
sin				+t
2
	π				= −sint
cos	2	+t

3π						= −cost
sin	2		−t

3π						= −sint
cos	2		−t

3π				+t
cos	2				= sint

3π						= −cost
sin	2		+t

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2615 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете Аналитическая геометрия