Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
researchgate.net Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Одесский государственный экологический университет
Предмет:
Аналитическая геометрия
Файл:
978-966-10-1272-0_Математика. Підручник для 10 класу. загальноосвітніх навчальних закладів. Рівень стандарту.pdf
Скачиваний:
981
Добавлен:
24.03.2018
Размер:
8.73 Mб
Скачать
☆
►Содержание►

§17. найпростіші тригонометричні рівняння і нерівності

Íайпростішими тригонометричними рівняннями називають рівняння: sin õ = a, cos õ = a, tg õ = a, ctg õ = à. Окремі з них розв’язувались у попередніх параграфах. Ãоловною особливістю тригонометричних рівнянь є те, що вони можуть мати безліч коренів, з чим пов’язані певні труднощі в пошуку і навіть у запису їхніх розв’язків. Íавчити подоланню цих труднощів є важливим завданням даного параграфа.

1. Рівняння sin x = a

Рівняння sin x = a будемо розв’язувати, користую-

чись тригонометричним колом або графіком функції y = sin x. Сутність першого способу, пов’язаного з тригонометричним колом, полягає у тому, щоб записати всі числа, яким відповідають точки тригонометричного кола з ординатою а.

Розглянемо наступний приклад.

Ïðèê ëàä 1. Розв’язати рівняння: sin x =

 

3

.

 

 

 

 

 

 

2

Знайдемо спочатку на тригонометрич-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ному колі точки з ординатою

3

. Таких то-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

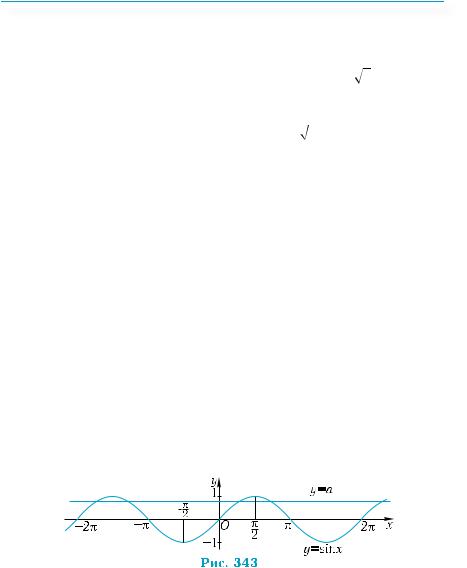
чок, очевидно, дві:

 

 

 

 

 

 

 

 

 

 

 

М1 і M2 (рис. 341). Вони

 

 

 

 

 

 

 

 

симетричні відносно осі ординат. Знайдемо

 

 

 

 

 

 

 

 

числа, яким відповідають ці точки. Оскільки

 

 

 

 

 

 

 

 

sin π =

3

, то числу

π відповідає точка М1, а

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

2

 

3

 

 

 

 

 

 

 

 

 

 

 

318

Розділ 3. Тригонометричні Функції

числу π −

π =

2π — точка М2, їй симетрична відносно осі ординат.

 

3

 

3

 

 

 

 

 

 

 

 

 

 

 

Справді,

 

2π

 

 

 

π

 

π

 

3

 

.

sin

 

 

= sin

π −

 

 

= sin

 

=

 

 

 

3

3

3

2

 

 

 

 

 

 

 

 

 

 

 

 

Таким чином, усі числа, яким відповідає точка М1, мають виг-

ляд π + 2πn,n Z ,

а

всі

числа,

яким

відповідає точка М2, —

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

23π + 2πn, n Z . Тобто множина розв’язків даного рівняння складається з двох серій чисел: x = 3π + 2πn, x = 23π + 2πn, n Z .

Відповідь. 3π + 2πn, 23π + 2πn, n Z .

Другий спосіб розв’язування тригонометричного рівняння sin x = a базується на застосуванні графіка функції y = sin x. Проілюструємо його на тому самому прикладі.

Побудуємо в одній системі координат графіки функцій

у = sin х і y = 23 (рис. 342). Вони перетинаються у безлічі точок. Завдання полягає в тому, щоб знайти абсциси цих точок.

На проміжку, довжина якого дорівнює найменшому додатному

періоду функції

у = sin х, тобто числу 2π, функція набуває усіх

своїх значень. Значення

 

3

 

на відрізку [0; 2π] вона набуває у

2

 

 

 

 

 

 

 

2π

 

 

3

 

2π

 

двох точках: х =

π

і х

=

, оскільки

sin π =

і sin

=

 

 

 

3

 

 

 

 

3

 

3

2

3

 

 

π

π

 

3

 

 

 

 

 

 

 

 

 

 

 

= sin π −

= sin

 

=

 

. Отже, враховуючи, що періоди синуса

3

2

 

3

 

 

 

 

 

 

 

 

 

 

 

 

дорівнюють 2πп, n Z, п ≠ 0, множину розв’язків даного

Найпростіші тригонометричні рівняння і нерівності

 

 

 

319

рівняння

можна записати у вигляді

двох серій чисел:

x = π + 2πn, x = 2π + 2πn, n Z.

 

 

 

 

 

3

3

 

 

 

3

 

Наведені способи розв’язання рівняння

sin x =

 

відрізня-

2

 

 

 

 

 

ються лише геометричним тлумаченням коренів цього рівняння.

Запис

усіх розв’язків рівняння sin x =

3

став

можливим,

2

 

 

 

 

 

 

оскільки нам вдалось вказати два корені цього рівняння, яким

відповідають на тригонометричному колі (чи на графіку) дві різні

точки. Якщо розв’язувати рівняння sinx = 0,3 , то ми поки що не

можемо цього зробити, оскільки не знаємо способу запису чисел,

синус яких дорівнює 0,3. Таким чином, для розв’язування рівнян-

ня sin х = а (|a| < 1) потрібно навчитись знаходити принаймні два

числа, синус яких дорівнює а, і яким відповідають на тригонометричному колі дві різні точки.

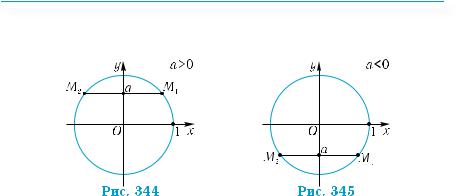
Розглянемо геометричну ілюстрацію розв’язків рівняння

sin х = а. Для цього побудуємо графіки функцій у = sin х, у = а (рис. 343). Якщо |а| > 1, то ці графіки не перетинаються, тобто дане рівняння не має розв’язків. Якщо |а| ≤ 1, то пряма у = а безліч разів перетинає графік функції у = sin х, тобто рівняння sin х = а має безліч розв’язків. Зокрема, якщо а = 1, то точки перетину мають

вигляд x = 2π + 2πn ; при а = –1 графіки перетинаються в точках x = − 2π + 2πn, n Z .

 

π

;

π

 

 

 

 

Нехай |а| ≤ 1. На відрізку −

2

функція у = sin x зростає

 

 

2

 

 

 

 

і набуває усіх значень від –1 до 1. При кожному а [–1, 1] пря-

ма у = а перетинає на цьому відрізку графік функції у =sin

х

лише

в одній точці, тому рівняння sin

 

−

π

;

π

х = а має на відрізку

2

 

 

 

 

 

 

 

2

320

Розділ 3. Тригонометричні Функції

один корінь. Цей корінь називають арксинусом числа а і позначають так: х = arcsin a.

Арксинусом числа а називається таке число з про-

 

 

π

;

π

, синус якого дорівнює а.

 

 

 

 

міжку −

2

 

 

 

 

 

 

 

2

 

π

 

π

 

Таким чином,

запис х = arcsin a означає: 1) −

≤ x ≤

і

 

 

 

 

 

2

 

2

 

2) sinx = a.

!Звертаємо увагу на те, що arcsin a визначено тільки для

–1 ≤ а ≤ 1.

Арксинуси довільних конкретних чисел із проміжку [– 1; 1] можна знаходити наближено за допомогою математичних таблиць чи калькуляторів.

Приклад 2. Обчислити:1) arcsin1 ;2)

 

 

2

 

;3)

arcsin0,6 .

arcsin

−

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

1) Оскільки 1 = sin π і −

π

< π <

π

, то arcsin

1

= π . Підкрес-

 

 

 

 

 

 

2

 

 

 

 

 

 

6

2

6

2

 

 

 

 

2

6

 

 

 

 

 

лимо, що хоча sin

5π

=

1

, але

arcsin1

≠

5π , бо

5π

міститься поза

 

 

 

 

 

 

6

 

 

2

 

 

2

 

6

 

6

 

 

 

 

 

 

 

межами проміжку

 

π

;

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

2

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) Оскільки

 

 

 

2

 

 

 

 

π

 

 

π

і

 

π

 

π

 

π

, то

 

 

 

−

 

 

 

 

 

= −sin

 

= sin

−

 

 

−

2

≤ −

4

≤

2

 

 

 

 

2

 

 

 

4

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

π .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

arcsin −

= −

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

Зверніть увагу на те, що arcsin

−

= −arcsin

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)Послуговуючиськалькулятором,знайдемо:arcsin0,6≈ 0,644.

 

 

Відповідь. 1)

π ; 2)

 

−

π ; 3) ≈ 0,644.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–1

Запишемо у загальному вигляді розв’язок рівняння sin х = а,

< а < 1. На тригонометричному колі містяться дві точки з орди-

Найпростіші тригонометричні рівняння і нерівності

321

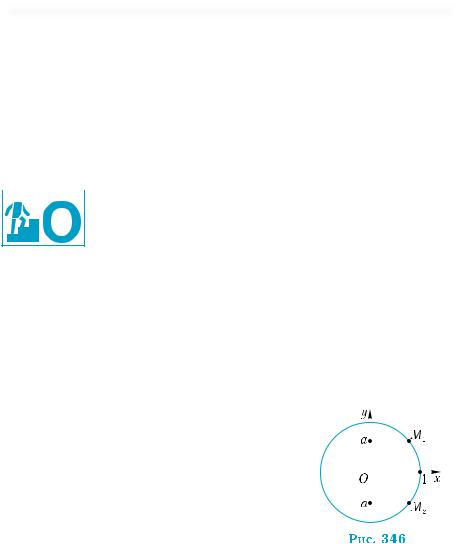
натою а (рис. 344, 345). Одним з чисел, якому відповідає точка М1, є число arcsin а, а числу (π – arcsin а) відповідає точка М2. Таким

чином, враховуючи, що числа 2πп, n Z, п ≠ 0, є періодами функції у = sin х, розв’язки рівняння sin х = а при |а| < 1 мають такий вигляд:

х = arcsin а + 2πп, х = π – arcsin а + 2πп, n Z.

Обидві ці формули можна записати у скороченій формі:

x = (−1)k arcsina + πk, k Z.

Одержана формула дає ті самі значення х, що і дві попередні формули, якщо розглянути випадки k = 2п, k = 2n +1, n Z. Справ-

ді,приk =2n маємо: x = (−1)2n arcsina + π 2n = arcsina + 2πn; приk = =2n+1 маємо: x = (−1)2n+1 arcsina + π (2n +1) = (−1)2n (−1) arcsina +

+ 2πn + π = π −arcsina + 2πn.

Повернемось до розв’ язків рівняння sinx = 0,3 . Їх можна записати так:

x = arcsin 0,3 + 2πk, k Z , x = π – arcsin 0,3 + 2πk , k Z

або x = (−1)k arcsin0,3 +πk, k Z.

Розв’язкирівняньsinх=1іsinх=–1булознайденовище,асаме:

x =

π

+ 2πn, x = −

π

+ 2πn, n Z .

 

2

 

2

 

Знайдена загальна формула дає ті самі результати, тобто застосовна і при |а| = 1.

Розв’язки рівняння sin х = 0, за вказаною формулою, набувають вигляду: x = πn, n Z .

21 Математика, 10 кл.

322 Розділ 3. Тригонометричні Функції

Приклад 3. Розв’язати рівняння: 1) sin х = 0,7; 2) sin 2х = –0,8.

 

1) Розв’язок має вигляд: х = (–1)n arcsin 0,7 +

πп, п Z.

 

2) 2х = (–1)n arcsin (–0,8) + πп, п Z, х = 1 (–1)n arcsin (–0,8) +

 

πn

 

 

2

 

+

, п Z.

 

 

 

 

2

(–1)n arcsin 0,7 + πп, п Z;

 

 

 

 

 

Відповідь. 1)

 

 

2)

1 (–1)n arcsin (–0,8) +

πn

, п Z.

 

 

2

 

 

 

 

2

 

 

Число arcsin а має наступні важливі властивості.

Властив³сть 1. sin (arcsin а) = a.

Ця рівність випливає безпосередньо з означення арксинуса.

Властив³сть 2. arcsin (–а) = –arcsin а.

Для його доведення, згідно з означенням арксинуса, слід по-

казати:

 

 

 

 

 

 

 

 

 

 

 

 

1) sin(–arcsin a) = –a;

 

 

 

 

 

 

 

 

 

2) − π ≤ −arcsina ≤

π.

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

Перша рівність є наслідком непарності синуса і означення арк-

синуса. Друге співвідношення безпосередньо

випливає із означення арксинуса.

 

 

 

 

Тепер розв’язки рівняння sin 2х = –0,8 з

 

 

 

 

 

 

 

прикладу 3 можна

 

записати

у

вигляді

 

 

 

1

 

πn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

х = 2 (–1)n+1 arcsin 0,8 +

 

, п Z.

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

Властивість 2 має просту геометричну ін-

 

 

 

 

 

 

терпретацію (рис. 346). Точки М1

і

М2 відпо-

 

 

 

 

відають числам arcsin a і arcsin (–а). Ці числа є протилежними, оскільки відповідні дуги

симетричні відносно осі абсцис.

Практично важливим є вміння виділяти ті розв’язки тригонометричного рівняння, які задовольняють певну умову.

Найпростіші тригонометричні рівняння і нерівності

323

Ïðèê

2

. Знайти:

 

 

2

1)

усі розв’язки рівняння;

 

 

 

 

2)

його найбільший від’ємний корінь;

π

 

3π

3)

розв’язки, які належать проміжку

 

;

 

2

;

 

 

 

 

 

2

4)

розв’язки, які належать проміжку (−π;4π);

5)

розв’язки, які задовольняють умову cos x > 0.

 

1) Усі розв’язки рівняння мають вигляд:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

x = (−1)k arcsin

−

 

+ πk = (−1)k+1 arcsin

+ πk =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=(−1)k+1 π

+ πk, k Z.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) Усі розв’язки рівняння можна також

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

записати

у

вигляді

двох

серій

чисел:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

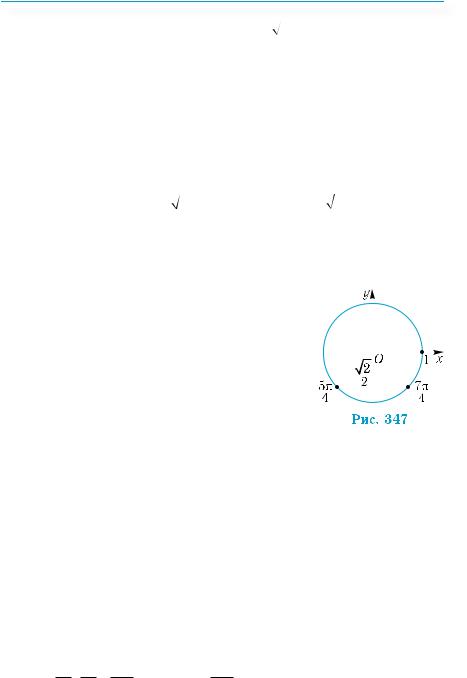
x = 5π + 2πn,

x =

7π

+ 2πn,n Z

(рис. 347).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найбільший від’ємний корінь можна одер-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

жати при

п

= –1. Відповідно маємо: х

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

=

5π −2π = −3π,

 

x =

7π

−2π = − π . Більшим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

4

π .

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

із них є число −

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

π

 

3π

 

 

 

 

 

 

5π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) Проміжку

 

;

належить корінь

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4) Щоб знайти ті розв’язки рівняння, які належать проміжку

(−π;4π),необхіднорозв’язативідноснопнерівності: −π <

5π

+ 2πn <

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

<

4π,

−π <

7π + 2πn < 4π. Послідовно матимемо:

 

−9π < 2πn < 11π,

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

4

 

−

11π

< 2πn <

9π

,

звідси

−9 < n <

11 ,

−11 < n < 9 ,n Z.

 

 

 

 

 

 

4

 

 

4

 

 

 

 

 

8

 

 

8

8

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отже, для обох серій п може набувати значень – 1, 0, 1 і тільки

цих значень. Тому шукані розв’язки знайдемо, якщо підставимо ці значення п у вирази для загальних розв’язків рівняння. Мати-

мемо: −34π, 54π, 134π; − 4π, 74π, 154π.

21*

324 Розділ 3. Тригонометричні Функції

5) Умову cos x > 0 задовольняє лише друга серія: x = 74π + 2πn,

n Z, оскільки лише ці числа відповідають точкам тригонометричного кола з додатними абсцисами.

Відповідь. 1) (−1)k+1 4π + πk, k Z;2) −4π ; 3) 54π ;

4) −34π, 54π, 134π; − 4π, 74π, 154π;5) 74π + 2πn,n Z .

Розв’язання складніших тригонометричних рівнянь зводиться до найпростіших за допомогою замін змінних, алгебраїчних перетворень, тригонометричних формул.

Ïðèê ëàä 5 . Розв’язати рівняння:

3sin2 x −5sin x −2 = 0 .

Це рівняння є квадратним відносно sin

х. Увівши заміну

sin x = t , дістанемо рівняння:

 

 

 

 

 

 

 

 

 

3t2 −5t −2 = 0.

 

 

 

Корені цього

рівняння

t = 2 і t = −1 . Рівняння sin х = 2

 

 

 

 

 

 

3

 

 

 

розв’язків не має. Розв’язки рівняння sin x = −1

мають такий ви-

гляд:

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

n

 

−

1

 

n+1

arcsin

1

+ πn , n Z.

x = (−1) arcsin

3

+ πn = (−1)

3

 

 

 

 

3 + πn , n Z.

 

 

Відповідь. (−1)

arcsin

 

 

 

 

n+1

 

 

 

1

 

 

 

 

Контрольні запитання

 

 

 

 

1°.

Чому дорівнює:

б) arcsin (–0,5);

 

в) arcsin 1?

 

а) arcsin 0,5;

 

2°.

Чи має зміст запис:

 

 

в) arcsin 1,3;

 

а) arcsin 0,3;

б) arcsin (–0,3);

 

 

г) arcsin (–1,5);

ґ) arcsin π;

 

д) arcsin

2 ?

3°.

Чи можна з рівності sin π

= 0 зробити висновок, що arcsin 0 = π?

4°.

Чи може рівняння sin х = а мати:

 

 

 

 

 

а) тільки один розв’язок;

б) тільки два розв’язки?

5°. Чи може arcsin а набувати значень:

 

 

3

 

 

а) π ; б) –π;

в) − π ;

г) π ; ґ)

2

; д) −

; е) 1,5?

 

 

 

6

3

2

 

2

 

Найпростіші тригонометричні рівняння і нерівності

325

6. При яких значеннях а справджується рівність sin (arcsin а) = а? 7. Скільки розв’язків рівняння sin х = 12 міститься на відрізку

[0; 8π]?

π

8. Як із загального розв’язку х = (–1)n 6 + пπ, п Z, рівняння

sin х = 12 знайти найменший додатний корінь цього рівняння?

2. Рівняння cos x = a

Рівняння cos х = а, так само як і рівняння sin x = a, будемо розв’язувати, користуючись тригонометрич- ним колом або графіком функції y = cos x. Потрібно навчитись записувати всі розв’язки цього рівняння. Необхідні міркування аналогічні тим, що проводились при розв’язанні рівняння sin х = а, тому наведемо їх стисло.

Якщо |а| > 1, то рівняння cos х = а не має розв’язків. При а = 1 пряма у = а перетинає графік функції у = cos х в точках х = 2πп, п Z. При а = –1 пряма у = а перетинає графік функції у = cos х в точках х = π + 2πп, п Z. При |а| < 1 рівняння cos х = а також має нескінченну кількість розв’язків.

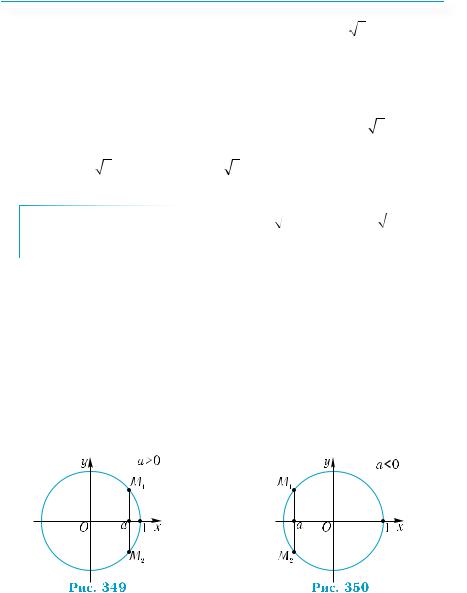
На відрізку [0, π] функція у = cos х спадає і набуває всіх значень від 1 до –1 (рис. 348). При довільному а [–1; 1] пряма у = а перетинає на цьому відрізку графік функції у = cos х в одній і тільки одній точці, тому рівняння cos х = а має на відрізку [0, π] тільки один корінь. Цей корінь називають арккосинусом числа а і позначають так: х = arccos a.

Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а.

Таким чином, запис х = arccos a означає: 1) 0 ≤ х ≤ π і 2) cos х = a. Як і arcsin a, arccos a визначено тільки для –1 ≤ а ≤ 1.

326

Розділ 3. Тригонометричні Функції

 

 

 

 

 

 

 

 

6 . Обчислити: 1) arccos 1

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

Ïðèê ëàä

; 2) arccos −

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

3) arccos (–0,2).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1) arccos 1 = π , оскільки

cos π

=

1

і 0 ≤

π

≤ π .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

3

 

 

 

 

3

 

 

2

 

 

 

 

3

 

 

 

 

 

 

3

 

 

 

2)

Зі

співвідношень cos(π − α) = −cosα

 

і

cos π

=

 

 

 

 

маємо:

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

5π

6

 

 

 

 

 

 

cos

 

π −

π

= −

 

, тобто arccos

 

−

 

 

= π −

π

=

, бо 0

≤

5π

≤ π.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

6

 

6

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

Зверніть увагу на те, що arccos

−

 

= π −arccos

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) Послуговуючись калькулятором, маємо: arccos(–0,2) ≈ 1,77.

 

Відповідь. 1)

π ; 2)

5π

; 3) ≈ 1,77.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Запишемо у загальному вигляді розв’язки рівняння cos х = а, –1 <а<1.НатригонометричномуколієдвіточкиМ1 іМ2 забсцисою а (рис. 349, 350). Одним із чисел, яким відповідає точка М1,є число arccos а, а одним із чисел, яким відповідає точка М2, є число –arccos а. Усі числа, яким відповідають точки М1 і М2, мають вигляд:

arccos а + 2πп і –arccos а + 2πп, п Z.

Таким чином, розв’язки рівняння cos х = а при |a| < 1 можна знайти за формулою:

х = ± arccos а + 2πп, п Z.

Найпростіші тригонометричні рівняння і нерівності

327

Розв’язки рівнянь cos х = 1 і cos х = –1 були знайдені вище, а саме:

x = 2πn, x = π + 2πn, n Z .

Загальна формула дає такі самі результати при |а| = 1.

Розв’язки рівняння cos х =

0 за вказаною

 

 

 

формулою набувають вигляду:

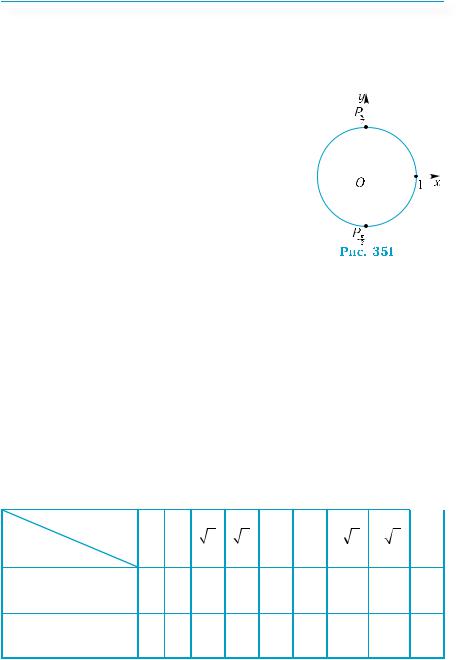
x = ± π + 2πn,

 

 

n Z . Але

 

 

 

 

2

 

 

 

їх можна записати простіше:

 

 

x = π + πn,

n Z ; адже числам, записаним

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

двома останніми формулами, відповідають

 

 

ті самі дві точки Pπ

і P

π тригонометрично-

 

 

 

 

2

−

2

 

 

 

 

го кола (рис. 351).

 

 

 

 

 

 

 

 

 

 

 

 

Ïðèê ëàä

7. Розв’язати рівняння: 1) cos х = 0,8; 2) cos 3х = –0,5.

1) Розв’язок має вигляд:

 

 

 

 

х = ± arccos 0,8 + 2πп, п Z.

2) Оскільки cos2π

= −0,5,

0 ≤

2π

≤ π , то

arccos(−0,5) =

2π , і

 

 

3

 

 

3

 

 

3

3x = ±

2π

+ 2πn,n Z , або x = ±

2π

+ 2πn , n Z .

 

 

3

 

 

9

 

3

 

 

Відповідь. 1) arccos 0,8 + 2πп, п Z; 2) x = ± 29π + 2π3n , n Z .

Скориставшись результатами розв’язування прикладів 2, 6, 7, наведемо таблицю значень arcsin х і arccos х для найбільш вживаних значень аргументу.

 

 

 

 

 

 

 

 

 

 

 

 

Таблиця 30

Значення х

0

1

2

3

1

–

1

–

 

2

 

–

 

3

–1

Вираз

 

2

 

 

 

 

2

 

 

 

 

 

 

 

2

2

 

 

2

 

 

2

 

arcsin x

0

π

π

 

π

π

–

π

–

π

 

–

π

– π

 

 

6

4

3

2

 

6

 

 

4

 

 

 

3

2

аrccos x

π

π

π

 

π

0

2π

3π

 

5π

π

2

3

4

6

3

4

6

 

 

 

328

Розділ 3. Тригонометричні Функції

Число arccos а має наступні важливі властивості.

Властив³сть 1. cos (arccos а) = a.

Ця рівність випливає безпосередньо з означення арккосинуса.

Властив³сть 2. arccos (–а) = π – arccos а.

Для її доведення, згідно з означенням арккосинуса, слід показати:

1) cos(π – arccos a) = –a; 2) 0 ≤ π −arccosa ≤ π. Перша рівність є наслідком формул зведення і означення арккосинуса: cos(π – arccos a) = –cos(arccos a) = –a. Друге співвідношення безпо-

середньо випливає з означення арккосинуса і властивостей нерів-

ностей: 0 ≤ arccosa ≤ π, −π ≤ −arccosa ≤ 0, 0 ≤ π −arccosa ≤ π.

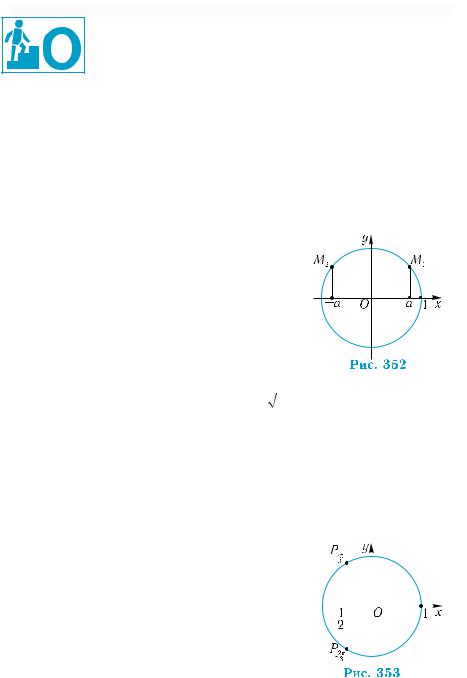
Властивість 2 має просту геометричну інтерпретацію (рис. 352). Точки М1 і М2 відповідаютьчисламarccosa іarccos(–а),ціточки симетричні відносно осі ординат, радіанні міри відповідних дуг доповнюють одна одну до π, тому arccos (–а) = π – arccos а.

Ïðèê ëàä 8 . Розв’язати рівняння: 2cos x +1

= 0.

 

sin x

 

 

Рівняння рівносильне системі

2cosx +1 = 0,

Розв’яжемо рів-

 

 

 

sinx > 0.

 

 

няння 2 cos x + 1 = 0 або cos x = −1 . Застосовуючи властивість 2,

 

 

 

 

 

1

2

 

1

 

 

 

 

 

 

матимемо: x

 

 

 

 

+ 2πn =

= ±arccos −

+

2πn = ± π −arccos

 

 

 

 

2π

 

2

 

2

 

 

 

 

 

 

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

=± π −

+ 2πn = ±

3

+ 2πn,n Z.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тепер із цих розв’язків відберемо ті, що за-

 

 

 

 

 

 

 

 

довольняють

нерівність

sin

x > 0. Скори-

 

 

 

 

 

 

 

 

стаємось тригонометричним колом. Розв’язки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

рівняння зображаються двома точками три-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

гонометричного кола (рис. 353). Але лише од-

 

 

 

 

 

 

 

 

ній із них (тій, що лежить у другій чверті)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

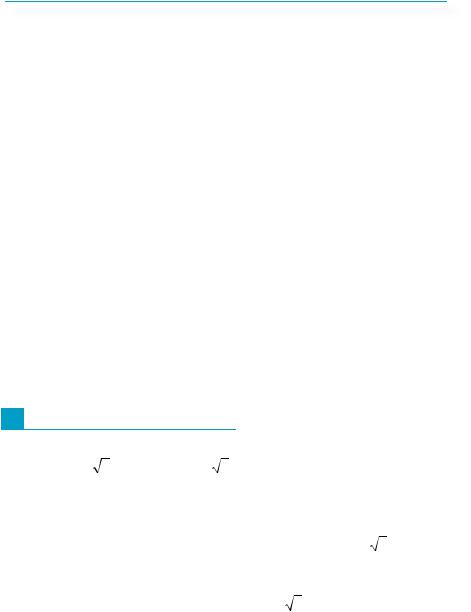
Найпростіші тригонометричні рівняння і нерівності

 

2π

329

відповідають числа х, для яких sin x > 0, а саме,

x =

+ 2πn,

п Z.

 

3

 

 

 

 

Відповідь.

2π

+ 2πn,n Z.

 

 

 

 

 

 

 

3

 

 

 

 

Застосування розглянутих у § 16 тригонометричних формул

дає змогу звести розв’язання більш складних тригонометричних

рівнянь до розв’язання найпростіших.

Ïðèê ëàä 9. Розв’язати рівняння: cos х + cos 3х = 4 cos 2х.

Перетворивши ліву частину згідно з формулою суми косину-

сів, дістанемо

2 cos 2х cos х = 4 cos 2х.

Звідси

cos 2х (cos х – 2) = 0.

 

Тоді cos 2х = 0 чи cos х = 2. Друге рівняння розв’язків не має, а

розв’язки першого мають такий вигляд:

 

2x = π

+ πn, x = π +

πn , n Z .

 

2

4

2

Відповідь. π

+ πn ,

n Z .

 

4

2

 

 

Контрольні запитання

1°.

Чому дорівнює:

 

 

 

 

 

 

 

 

 

 

 

 

а) arccos

2

 

 

 

 

2

 

 

 

 

 

;

б) arccos −

;

в) arcos (–1); г) arcos 0?

 

 

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

2°.

 

 

 

 

 

 

 

 

 

 

Чи має зміст запис:

 

 

 

 

 

 

в) arccos 1,3;

 

а) arccos 0,3;

б) arccos (–0,3);

 

г) arccos (–1,5);

ґ) arccos π;

 

д) arccos

2 ?

3°.

Який знак має число arcсos(–0,3)?

 

 

4°.

Чи може arccos

а набувати значень:

 

 

 

а) − π ;

б) π ;

в)

2π

;

г)

4π

;

ґ)

3 ; д) –1;

е) 3,5?

 

 

 

5.

3

4

3

 

 

 

 

3

 

 

 

 

При яких значеннях а справджується рівність cos (arccos а) = а?

330

Розділ 3. Тригонометричні Функції

6.Скільки розв’язків рівняння cos х = 12 міститься на відрізку

[0; 7π]?

7.Як із загального розв’язку х = ± 56π + 2πп, п Z, рівняння

cos х = − 23 одержати найбільший від’ємний корінь цього рівняння?

8.Якою заміною: sin x = z чи cos x = z — зручніше розв’язувати рівняння:

 

 

а) 2sin2 x − cos2 x +3sin x = 0;

б) 2sin2 x − cos2 x +3cos x = 0?

 

 

 

 

 

 

 

 

3. Рівняння tg x = a і ctg x = a

 

 

 

 

 

 

 

 

 

 

 

 

Розглянемо рівняння tg х = а. Оскільки множиною

 

 

 

 

 

 

 

 

 

 

 

 

значень тангенса є множина всіх дійсних чисел, то

 

 

 

 

 

 

це рівняння при кожному а має розв’язок. Пряма

 

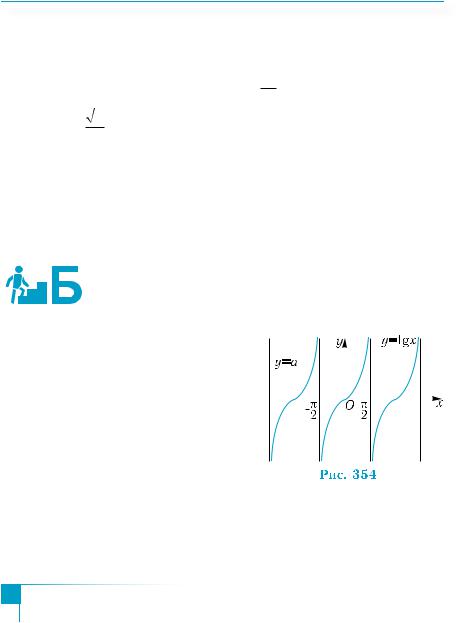
у = а перетинає графік функції у

= tg х безліч разів (рис. 354).

 

 

 

 

 

 

 

 

 

 

π

;

π

 

 

 

 

 

 

 

 

 

 

 

 

 

На проміжку

−

2

функція

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

y = tg x зростає і набуває кожного

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

свого значення лише один раз.

 

 

 

 

 

 

Тому рівняння tg х = а

на проміжку

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π

;

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

2

має тільки один корінь. Цей

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

коріньназиваютьарктангенсомчис-

 

 

 

 

 

 

 

 

 

 

 

 

ла а

і позначають так:

х = arctg а.

 

 

 

 

 

 

 

 

 

 

 

 

 

Арктангенсом числа а називається таке число з про-

 

 

 

 

 

π

;

π

тангенс якого дорівнює а.

 

 

 

 

 

 

 

 

міжку −

2

,

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Такимчином,записх=arctgаозначає:1) − π < x <

π і2) tg x = a .

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

!Звертаємо увагу на те, що arctg а визначено для всіх дійсних а.

Оскільки функція у = tg х періодична з періодами πп, п Z, п ≠ 0, то всі корені рівняння tg х = а знаходять за формулою:

х = arctg а + πп, п Z.

Найпростіші тригонометричні рівняння і нерівності

331

Ïðèê ëàä

10 . Обчислити: 1) arctg

3; 2) arctg(−1).

 

 

 

 

 

1) Оскільки tg

π

=

 

3 і −

π <

π

<

π ; то arctg

3 =

π.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

2

 

3

 

2

 

 

 

 

 

 

 

 

 

 

3

 

 

 

π

 

2)Оскільки tg

 

−

π

= −tg

π

= −1 і

−

π

< −

π

<

π

,то arctg (−1) = −

.

 

4

 

4

2

4

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь. 1)

 

π; 2) −

π.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

!

Зверніть увагу на те, що arctg(−1) = −arctg1.

 

 

 

 

 

 

Ïðèê ëàä

11.

 

 

Розв’язати рівняння: 1)

tg x =

1

 

;

2) tg x

= −2;

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

2

 

 

 

3) ctgx = −

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

1

 

 

 

 

 

 

 

 

 

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

x = arctg

 

 

 

 

+ πn, або x =

+ πn, n Z .

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2)

= arc tg(−2)+ πn,

n Z,

x = 2arc tg(−2)+ 2πn,

n Z.

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) Якщо ctgx = −

, то tg x = −

 

3 , і навпаки. Тому ці рівнян-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ня — рівносильні. Звідси x = arctg(−

3)+ πn =

 

 

 

 

 

 

 

 

 

 

 

= −

π

+ πn, n Z , бо

 

 

 

π

 

= −tg

π

= − 3

і

−

π

< −

π

<

π

.

 

 

 

 

3

tg −

3

 

3

2

3

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь. 1) π + πn,

n Z ; 2)

2arc tg(−2)+ 2πn, n Z

; 3)

−

π

+ πn,

n Z .

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язання рівняння ctg х = а можна звести до розв’язання рівняння tgx = 1a при а ≠ 0, а можна скористатися спеціальною

формулою.

Розглянемо рівняння сtg х = а.

Оскільки множиною значень котангенса є множина всіх дійсних чисел,

то це рівняння при кожному а має розв’язок. Пряма у = а перетинає

графік функції у = сtg х безліч разів

(рис. 355).

332

Розділ 3. Тригонометричні Функції

На проміжку (0; π) функція у = ctg х спадає і набуває кожного свого значення один раз. Тому рівняння ctg х = а при кож-

ному а на проміжку (0; π) має лише один корінь. Цей корінь нази-

вають арккотангенсом числа а і позначають так: х = arcctg а.

Арккотангенсом числа а називається таке число з проміжку (0; π), котангенс якого дорівнює а.

Таким чином, запис х = arcctg а означає: 1) 0 < x < π і 2) ctg х = а.

!Звертаємо увагу на те, що arcсtg а визначено для всіх дійсних а.

Оскільки функція у = ctg х періодична з періодами πп, п Z, п ≠ 0, то всі корені рівняння ctg х = а знаходять за формулою:

х = arcctg а + π п, n Z.

Ïðèê ëàä 12 . Розв’язати рівняння: 1)ctg х = –1;

2)(tg x + 2)( 3 ctg х – l) = 0.

1) Оскільки ctg 34π = −1 і 0 < 34π < π, то arcctg(−1) = 34π. Тому

x= arcctg(−1)+ πn = 34π + πn, n Z.

! Звертаємо увагу на те, що arcctg(−1) = π −arcctg1.

2) Наслідком даного рівняння є сукупність рівнянь: tgx + 2 = 0

і3 ctg x −1 = 0 . Розв’яжемо перше рівняння сукупності: tgx = −2;

x= arctg(−2) + πn,n Z. Встановимо, чи є знайдені числа кореня-

ми даного рівняння. Оскільки при цих значеннях х вираз у других дужках має зміст (адже з рівності tg х = –2 випливає, що ctg х =

= −12 ), то знайдені значення х є коренями даного рівняння. Роз-

в’яжемо друге рівняння сукупності: ctgx =

1

, x = arc c tg

1

+ πn =

3

3

 

 

 

= 3π + πn, n Z. При цих значеннях х вираз у перших дужках має

зміст, тому знайдені значення х є коренями даного рівняння.

Відповідь. 1) 34π + πn, n Z; 2) arctg (–2) + πп; 3π + πn, n Z.

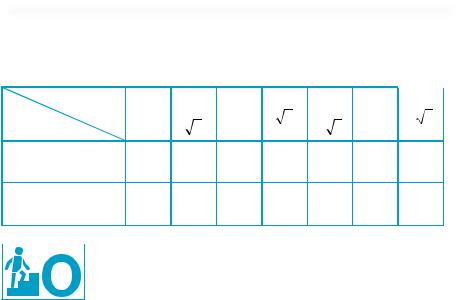
Найпростіші тригонометричні рівняння і нерівності

333

Скориставшись результатами розв’язування прикладів 10 – 12 й ін., складемо таблицю значень arctg х і arcctg х для найбільш уживаних значень аргументу.

Значення х

 

 

 

 

 

 

 

Таблиця 31

0

1

1

3

−

 

1

–1

–

3

Вираз

3

 

3

 

 

 

 

 

 

 

 

arctg x

0

π

π

π

−

π

− π

−

π

 

 

 

6

4

3

 

 

6

4

 

3

arcctg x

π

π

π

π

2π

3π

5π

2

3

4

6

3

4

6

 

 

 

Числа arctg а і arcctg а мають наступні важливі

 

 

властивості.

 

 

 

 

 

 

 

 

 

Властив³сть 1. tg(arctgа)= a;ctg(arcctgа)= a.

Ці рівності випливають безпосередньо з означень арктангенса і арккотангенса.

Властив³сть 2. arctg(–а) = –arctg а; arcctg(–а) = π –arcctg а.

Доведемо другу з цих рівностей. Для цього, згідно з означенням арккотангенса, слід показати:

1) ctg(π – arcctg a) = –a; 2) 0 < π −arcctga < π.

Перша рівність є наслідком формул зведення і означення аркко-

тангенса: ctg(π – arcctg a) = –ctg(arcctg a) = –a. Друге співвідношення безпосередньо випливає з означення арккотангенса і властивостей нерівностей: 0 < arcctga < π, −π < −arcctga < 0, 0 < π − arcctga < π.

Перша рівність доводиться аналогічно.

Наведені рівності мають просту геометричну інтерпретацію. Точки М1 і М2 на лінії тангенсів (рис. 356) відповідають числам arctg a і arctg (–а). Ці числа є протилежними, оскільки відповідні дуги на тригонометричному колі симетричні відносно осі абсцис.

Точки М1 і М2 на лінії котангенсів (рис. 357) відповідають числам arcctg a і arcctg (–а). Ці точки симетричні відносно осі ординат, радіанні міри відповідних дуг на тригонометричному колі доповнюють одна одну до π, тому arcctg (–а) = π – arcctg а.

334

 

 

 

 

 

Розділ 3. Тригонометричні Функції

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ïðèê ëàä 13 . Розв’язати рівняння: x −1ctgx = 0.

Область визначення даного рівняння визначається співвідношенням: x – 1 ≥ 0, x ≠ πn,n Z. Його наслідком є сукупність

рівнянь: x −1 = 0, ctgx = 0, розв’язками яких є відповідно числа:

x =1, x = π + πn,n Z. Остання серія розв’язків належить області

2

 

 

 

 

 

визначення рівняння, тобто задовольняє умову х ≥ 1, лише при

цілих невід’ємних значеннях п.

 

 

 

Відповідь.

x =1, x = π + πn,n = 0,1,2,....

 

 

 

 

2

 

 

 

Ïðèê ëàä 14. Розв’язати рівняння: tg x +3ctg x = 2 3.

Позначимо tg х через у. Тоді ctg x =

1

=

1 , і рівняння на-

tg x

 

 

 

 

y

буває вигляду:

y + 3 = 2 3 або y2 −2 3y +3 = 0.

 

 

 

y

 

 

 

Знайдене рівняння має один корінь

3 . Розв’язком рівняння

tg x = 3 є x =

π

+ πn, n Z.

 

 

 

 

3

 

 

 

 

Відповідь.

π

+ πn, n Z.

 

 

 

У рівнянні

3

 

 

 

 

 

 

 

 

 

asin2 x +bsin x cos x + ccos2 x = 0

кожен доданок має степінь 2. Таке рівняння називається однорідним рівнянням другого степеня відносно sin х і cos x. Вза-

галі, рівняння з невідомими u i v, в якому кожен з доданків

має один і той самий степінь відносно невідомих, називається однорідним відносно u i v.

Найпростіші тригонометричні рівняння і нерівності

335

Такі рівняння розв’язуються діленням на старший степінь косинуса чи синуса.

Ïðèê ëàä 15 . Розв’язати рівняння:

4 sin2 x −8sin x cos x +10cos2 x = 3.

Замінимо 3 на 3(sin2 x + cos2 x) :

sin2 x −8sin x cos x +7cos2 x = 0 .

Дістали однорідне рівняння другого степеня. Розділимо обидві його частини на cos2 x .

!Втрати розв’язків при цьому не буде, оскільки cos х і sin х не можуть одночасно дорівнювати нулю.

Отже,

 

 

 

 

 

sin2 x

 

−8

sin x

 

+7 = 0, tg2x −8tg x +7 = 0;

tg x =1 або tg x = 7;

cos2 x

cos x

 

 

 

 

 

 

x = π + nπ, x = arctg7+ nπ,

n Z .

Відповідь. π

4

 

+ nπ, arctg7+ nπ, n Z.

 

 

 

4

 

 

Контрольні запитання

1°.

Чому дорівнює:

 

 

 

 

 

 

 

 

 

 

 

 

 

а) arctg 1;

 

б) arctg (–1);

 

в) arcctg

 

3;

 

г) arcctg (−

3 );

ґ) arctg 0;

 

д) arcсtg 0?

2°.

Чи можна з рівності tg π = 0 зробити висновок, що arctg 0 = π?

3°.

Який знак має число:

 

 

б) arcсtg(–2,3)?

 

 

 

 

а) arctg(–2,3);

 

 

 

 

 

 

 

4°.

Чи може arctg а набувати значень:

 

 

 

 

3

 

 

а) π ;

б)

π ;

в) −π

;

г) − π ;

ґ)

2 ; д) −

 

 

; е) 1,5?

 

 

2

5°.

6

 

3

 

 

 

3

 

 

 

 

Чи може arcctg а набувати значень:

 

 

 

 

 

 

 

а) π ;

б) 0;

в) −

π

;

г)

3π

;

ґ) 4;

д) –1;

 

е) π ?

 

2

 

 

6.

2

 

 

 

 

4

 

 

 

 

 

 

 

При яких значеннях

а

справджується рівність:

 

 

 

 

a) tg (arctg

а) = а;

 

 

 

 

б) arctg (tg а) = а?

 

 

 

336

Розділ 3. Тригонометричні Функції

7.Чи може рівняння ctg x = а: а) мати рівно один розв’язок; б) мати рівно два розв’язки; в) не мати жодного розв’язку?

8.Скількирозв’язківрівнянняtgх=1міститьсянавідрізку[0;5π]?

9.Чому дорівнює найменший додатний корінь рівняння tg х = –2?

10.Чи однорідні відносно sin х і cos х такі рівняння:

 

a) sin х + 3 cos х = 0;

б) sin2 x −2cos2 x +3sin x cos x = 0;

 

в) sin2 x + 2sin x − cos2 x = 0; г) sin3 x −3sin2 x cos x + cos3 x = 0;

 

ґ) 4 sin2 x −8sin x cos x +10cos2 x = 3 ?

 

 

 

4. Найпростіші тригонометричні нерівності

 

 

Найпростіші

тригонометричні

нерівності, як

 

 

 

 

і найпростіші тригонометричні рівняння, можна

 

 

розв’язувати за допомогою графіків тригонометрич-

 

них функцій

та тригонометричного кола. Розглянемо на прикла-

дах загальні підходи до їхнього розв’язання.

 

 

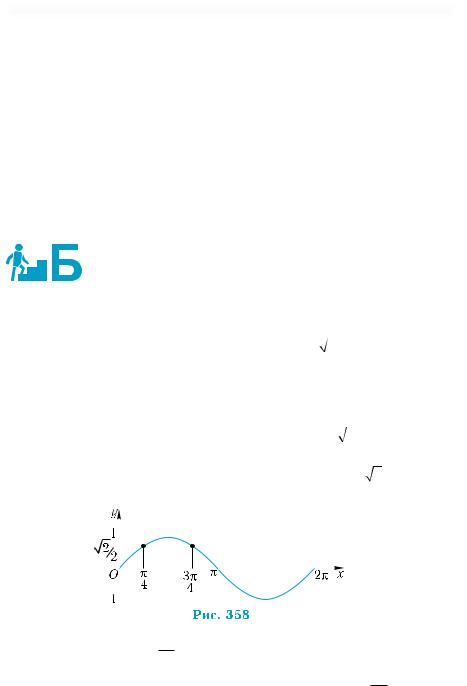
Ïðèê ëàä 16 . Розв’язати нерівність: sinx ≥

2

.

2

 

 

 

 

 

Оскільки синус — періодична функція з періодом 2π, то досить

знайти розв’язки нерівності на довільному проміжку завдовжки 2π,

наприклад, на відрізку [0, 2π].

2

 

 

 

Розглянемо графіки функцій у = sin х і y =

 

на відрізку

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

[0, 2π] (рис. 358). На цьому відрізку рівняння sin x =

має два

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

розв’язки: х = 4π і x = 34π , тому всі розв’язки даної нерівності на відрізку [0, 2π] визначаються співвідношенням 4π ≤ x ≤ 34π. Врахо-

Найпростіші тригонометричні рівняння і нерівності

337

вуючи періодичність функції у = sin х, паралельним перенесен-

ням проміжку

 

π

;

3π

вправо і вліво на 2π, 4π, … , одержимо:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π + 2πn ≤ x ≤

3π + 2πn, n Z.

Цей

 

запис

 

означає, що

 

 

множина

4

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15π

 

13π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

; −

розв’язків нерівності є об’єднанням проміжків: ..., −

 

4

 

,

 

 

7π

 

 

 

5π

 

 

 

 

 

 

3π

9π

 

11π

 

17π

 

19π

 

 

 

 

 

 

 

 

 

4

 

; −

 

,

π

;

;

 

;

,... .

 

 

 

 

 

 

 

 

 

−

4

4

 

 

4

 

,

 

4

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

4

 

 

 

 

4

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скорочено це об’єднання проміжків будемо записувати так:

π

+ 2πn;

3π

 

 

 

 

 

 

, n Z.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

+ 2πn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’яжемо ту саму нерівність за допомогою тригонометрично-

го кола.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Позначимонатригонометричномуколіточ-

 

 

 

 

 

 

ки,ординатиякихдорівнюють

 

 

2

(рис.359).Для

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

цього через точку на осі ординат з ординатою

 

 

 

 

 

 

 

 

 

 

 

 

 

2

проведемо пряму, паралельну осі х, яка

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

перетинає тригонометричне коло в точках

 

 

 

 

 

 

Pπ i P3π . Ординати всіх точок дуги

Pπ BP3π є

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

4

 

 

 

 

 

 

 

 

 

 

більшими від

 

 

2

 

або дорівнюють

 

2

. Тому на відрізку [0, 2π]

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дану нерівність задовольняють всі значення х, для яких

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π

≤ x ≤

3π.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

З урахуванням періодичності функції у = sin х маємо той са-

мий результат:

π

 

+ 2πn ≤ x ≤

3π + 2πn, n Z.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

3π

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь.

 

π

+ 2πn;

 

 

 

 

 

n Z.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

4

+ 2πn ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22 Математика, 10 кл.

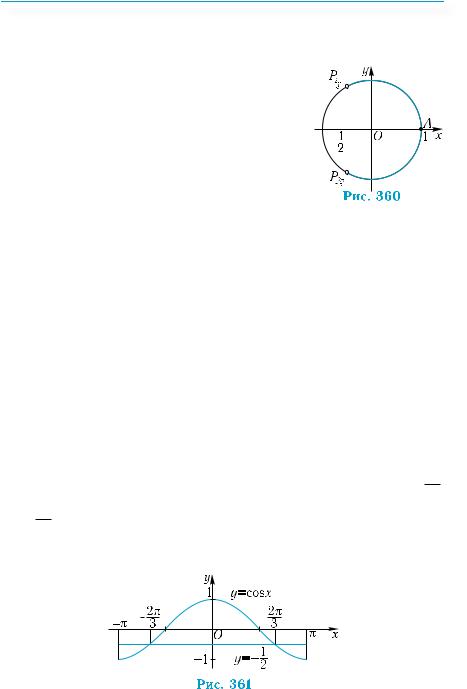
338

Розділ 3. Тригонометричні Функції

Ïðèê ëàä 17.

Розв’язати нерівність: сos х > −

1 .

 

Через точку на осі абсцис з абсцисою

2

 

 

 

 

 

 

 

 

−1

(рис. 360) проведемо пряму, паралельну

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

осі у. Ця пряма перетинає тригонометричне

 

 

 

 

 

 

коло в

 

точках

P

i P

 

. Всі точки дуги

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2π

−

2π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

3

 

 

 

 

 

 

 

 

P

AP

 

, окрім її кінців, мають абсцису біль-

 

 

 

 

 

 

−2π

2

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

3

 

 

 

 

 

 

 

 

 

 

 

 

шу, ніж −12 . Тому на відрізку [–π;π]розв’язки даної нерівності визначаються співвідношенням

−23π < x < 23π.

Зурахуванням періодичності функції у = сos х матимемо:

−23π + 2πn < x < 23π + 2πn, n Z.

Розв’яжемо цю нерівність за допомогою графіка функції у = сos х.

Оскільки косинус — періодична функція з періодом 2π, то доситьзнайтирозв’язкинерівностінадовільномупроміжкузавдовжки 2π, наприклад, на відрізку [–π; π]. Зручність вибору саме цього відрізку стане зрозумілою далі.

Розглянемо графіки функцій у = cos х і y = −12 на відрізку [–π; π] (рис. 361). На ньому рівняння cos x = −12 має два розв’язки: х = −23π

і x = 23π . Потрібно знайти всі ті значення х, для яких відповідні точ-

ки графіка функції у = cos х містяться вище прямої y = −12 . На від-

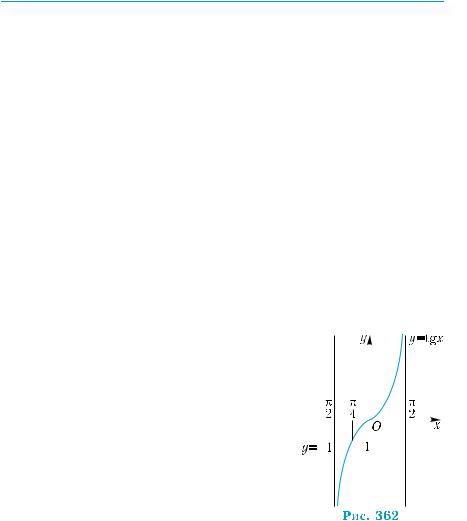
Найпростіші тригонометричні рівняння і нерівності

339

різку [–π; π] всі розв’язки даної нерівності визначаються співвід-

ношенням −2π < x < 2π. З урахуванням періодичності функції

 

3

3

у = cos х множину розв’язків нерівності можна записати так:

−

2π + 2πn < x <

2π + 2πn, n Z.

 

3

3

 

Якби ми вибрали відрізок [0, 2π], то розв’язки даної нерівності

на цьому відрізку не утворювали б суцільний проміжок, а склада-

лись з двох інтервалів:

 

0;

2π

 

4π

 

 

 

3

і

 

3

 

; 2π . Усі розв’язки даної не-

рівності складали

б

 

 

 

 

 

 

 

 

об’єднання

двох

сукупностей проміжків:

 

2πn;

2π

 

 

 

і

4π

 

 

 

 

 

 

 

 

, n Z.. Як бачимо, вибір від-

 

 

3

 

+ 2πn

 

 

+ 2πn; 2π + 2πn

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

різка [–π; π] привів до більш зручного запису розв’язку.

 

 

Відповідь.

 

 

2π

+ 2πn;

2π

 

 

 

 

n Z.

 

 

 

−

3

3

+ 2πn ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ïðèê ëàä

18 . Розв’язати нерівність: tg х ≥ –1.

 

 

Оскільки тангенс — періодична функ-

ція з періодами

πп,n Z,n ≠ 0 ,

то досить

 

 

 

 

 

знайти розв’язки нерівності на довільному

 

 

 

 

 

проміжку

завдовжки

 

π,

наприклад,

на

 

 

 

 

 

 

 

π

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

2

;

2

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розглянемо графіки функцій у = tg х

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

і

 

 

 

 

 

 

 

 

 

−

π

;

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

у = –1 на

2

(рис. 362). На цьому про-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

= –1 має один розв’язок

 

 

 

 

 

міжку рівняння tg x

 

 

 

 

 

x = −

π

. Для розв’язання нерівності потріб-

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

но знайти всі ті значення х, для яких відповідні точки графіка

у = tg x

розташовані вище прямої

у = –1 або ж належать цій пря-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

π

;

π

 

всі розв’язки даної нерівності визнача-

мій. На проміжку −

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ються умовою:

− π

≤ x <

 

π

. Оскільки періодами тангенса є числа πп,

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22*

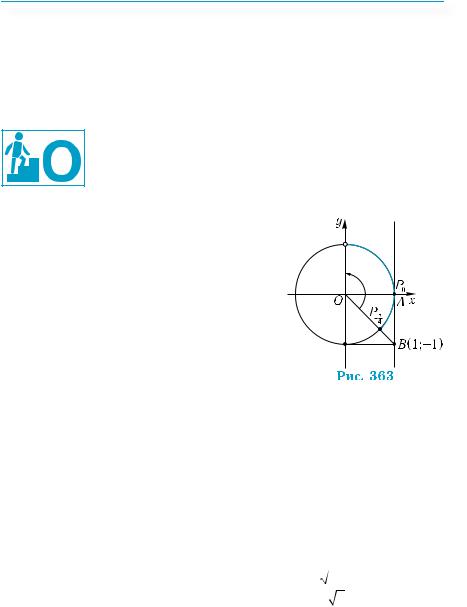
340

Розділ 3. Тригонометричні Функції

n Z , п ≠ 0, то множину розв’язків даної нерівності можна записа-

ти так: −

π

+ πn ≤ x <

π

+ πn, n Z.

 

4

 

 

π

 

2

 

π

 

 

Відповідь.

+ πn;

, n Z.

−

4

2

+ πn

 

 

 

 

 

 

 

 

 

Найпростіші тригонометричні нерівності, пов’язані

зтангенсомікотангенсом,можнатакожрозв’язувати

за допомогою ліній тангенсів і котангенсів на три-

гонометричному колі. Покажемо їхнє застосування

до нерівності, розглянутої у прикладі 18.

Відмітимо на лінії тангенсів точку

В(1; –1) (рис. 363). Зверніть увагу на те,

що абсцисою точки В є абсциса точки Р0

(усі точки на лінії тангенсів мають ту

саму абсцису, що дорівнює 1), через яку

проходить лінія тангенсів, а ордина-

тою — число, яке стоїть у правій частині

нерівності. Сполучимо точку В відрізком

прямої з центром кола. Цей відрізок пе-

ретинає коло у точці P

π , що відповідає

−

4

числу − π , тангенс якого дорівнює –1. Для розв’язання нерівності

4

 

 

 

 

 

 

 

 

потрібно знайти всі ті значення х, для яких відповідні точки лінії

 

 

 

−

π

;

π

 

всі

тангенса розташовані не нижче точки В. На проміжку

2

2

 

 

 

 

 

 

 

 

розв’язки даної нерівності визначаються умовою: −

π

≤ x <

π

. З

 

 

4

 

 

 

 

2

 

урахуванням періодичності функції у = tg х одержали ту саму від-

повідь, що і раніше.

 

 

 

 

 

 

 

 

Ïðèê ëàä 19. Розв’язати нерівність: ctg х <

3 .

 

 

 

 

 

 

 

Відмітимо на лінії котангенсів точку B(

3; 1)

(рис.

364).

Знову звертаємо вашу увагу на те, що ординатою точки є число 1 — ордината точки Pπ , через яку проходить лінія котангенсів,

а абсцисою — число, що 2стоїть у правій частині розв’язуваної не-

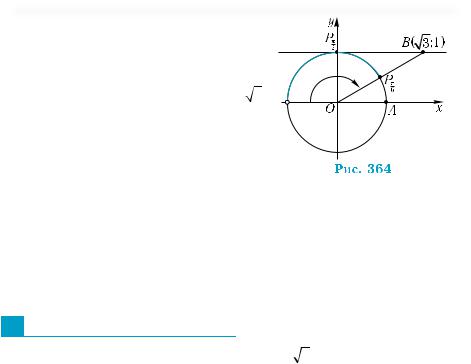
Найпростіші тригонометричні рівняння і нерівності

341

рівності. Сполучимо точку В відрізком

прямої з центром кола. Цей відрізок

перетинає коло у точці Pπ , відповідній

6

 

числу π , котангенс якого дорівнює

3 .

6

 

Для розв’язання нерівності потрібно

знайти всі ті значення х, для яких від-

повідні точки лінії котангенсів розта-

шовані лівіше від точки А. На проміж-

ку (0; π) всі розв’язки даної нерівності

визначаються умовою: π < x < π. Отже, з урахуванням періодич-

 

 

 

 

 

 

6

π + πn < x < π + πn, n Z.

ності функції у = ctg х маємо:

 

 

 

 

 

π

 

 

6

 

 

 

 

 

 

 

 

 

 

 

, n Z.

 

 

 

 

 

 

Відповідь.

+ πn; π + πn

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

Контрольні запитання

 

 

 

 

 

1°.

Чи можна розв’язки нерівності sin x ≥

 

2

 

записати у вигляді

2

 

 

 

 

3π

+ 2πn ≤ x ≤ π + 2πn, n Z?

 

 

 

 

−

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

4

 

 

 

 

 

 

2°.

Чи можна розв’язки нерівності сos х > −1

записати у вигляді

 

 

4π

 

 

8π

 

 

2

 

 

 

 

+ 2πn ≤ x ≤

+ 2πn, n Z?

 

 

 

 

 

 

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3°. Чи має розв’язок нерівність:

 

в) cos x ≥1

?

 

a) sin x ≤ −1 ;

 

б) cos x >1 ;

 

4.

Чи

збігаються множини

розв’язків

нерівностей

tg х ≥ –1

 

і сtg

х ≤ –1?

 

 

 

 

 

 

 

 

5*. При яких значеннях а всі дійсні числа задовольняють нерів-

ність:

б) sin x ≥ a ;

в) sin х < а;

г) sin x ≤ a ?

a) sin х > а;

6*. При яких значеннях а не має розв’язків нерівність:

a) cos х > а;

б) cos x ≥ a ;

в) cos х < а;

г) cos x ≤ a ?

7*. Чи існує значення а, при якому всі дійсні числа задовольня-

ють нерівність:

б) tg х ≥ a ;

в) tg х < а?

а) tg х > а;

342

Розділ 3.

Тригонометричні Функції

8*. Чи може не мати розв’язків нерівність:

в) ctg х > а?

a) tg х < а;

б) cos x ≥ a ;

Задачі

353°. У якій чверті тригонометричного кола лежить точка Pt,

якщо:

 

 

 

 

2) t = arcsin (–0,8);

 

 

 

 

1) t = arcsin 0,6;

 

 

 

 

 

 

 

3) t = arccos 0,8;

 

 

 

4) t = arccos (–0,6)?

 

 

 

 

354. Обчисліть:

1

 

 

 

 

 

 

 

1

 

 

 

 

1°)

 

;

 

 

2°)

 

 

−

 

 

 

sin arccos

 

 

 

sin arcsin

 

;

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

3°)

 

 

2

 

 

4°)

 

 

 

2

 

 

 

 

cos arcsin

−

 

;

cos arccos

−

 

 

 

;

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5) sin(arccos0,6);

 

 

6) cos(arcsin (−0,8)).

 

 

355°. Розв’яжіть рівняння:

1) sin2x = 23 ;

3) cos x2 = −12 ;

5) sin x2 = 1 +2 3 ;

7) 2 sin 3x = −1 ;

9) 9sin2x = –1;

11) (1– 2 cos х)(3 – 2sinx) =

13) sin 3x = 0,2;

356.Знайдіть нулі функції:

1) y = 2sin x +1;

2) y =

1

 

 

2

2)

 

 

 

 

π

 

 

 

 

2

;

sin

3x +

 

 

 

= −

 

 

4

 

2

 

 

 

 

 

 

 

 

 

4)

 

 

π

 

 

3

;

 

cos x −

 

 

 

=

 

 

 

4

2

 

 

 

 

 

 

 

 

 

 

 

6)

 

2x −

 

π

 

= 4 − 7 ;

cos

3

 

 

 

 

 

 

 

 

 

 

 

8)

4 sin2 x = 3 ;

 

 

 

 

 

10) (2 sin х + 1) (1 + cos x) = 0; 0; 12) cos 2x = –0,6;

14) cos (х + 0,5) = 0,9.

sin x −

2

; 3)

y = 2cosx + 2.

4

 

 

 

357. Розв’яжіть рівняння:

 

 

 

 

 

1)

 

sin x

= 0 ;

2)

sin x

= 0 ;

3)

1 + cos2x

= 0 .

1 + cos x

sin3x

1 −sin x

 

 

 

 

 

 

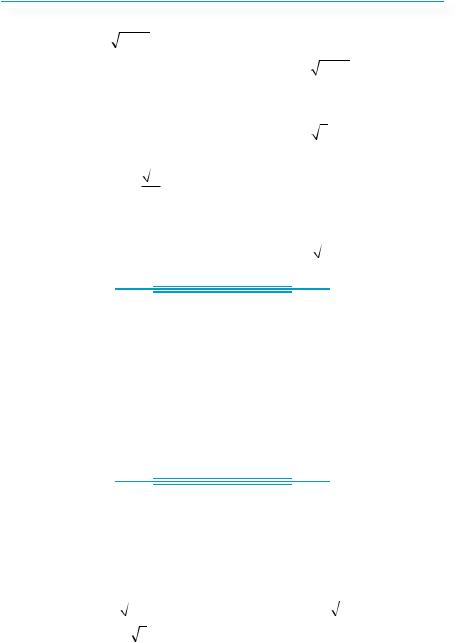
Найпростіші тригонометричні рівняння і нерівності

 

343

358. Укажіть всі нулі функції:

 

 

 

 

1)

y = sin x

 

cos x ;

 

 

 

2)

y = cos x tgx +1 ;

3)

y = sin 1

;

 

 

 

 

 

4)

y = cos x

sin x .

 

x

 

 

 

 

 

 

 

 

 

 

359*. Знайдіть розв’язки рівняння, які належать указаному про-

міжку:

1

 

 

 

3π

 

 

 

2

 

1)

 

 

 

 

 

; 2)

cos2x =

, x [0;6π] ;

sinx = −

 

 

, x

−

 

;2π

 

2

2

2

 

 

 

 

 

 

 

 

3)

sin x − π = 3 , x [−π; 3π] .

 

 

 

2 4 2

360.Знайдіть розв’язки рівняння, які задовольняють наведену умову:

1) cos2x = 0, cos x < 0 ;

2) cosx = −

3

,sin 2x < 0 .

2

 

 

 

361.Знайдіть:

1)величину кутів ромба, якщо відношення його периметра до однієї з діагоналей дорівнює 3;

2)величину гострих кутів прямокутного трикутника, якщо його висота поділяє гіпотенузу у відношенні 1:3.

362.Виразіть:

1)гострі кути прямокутного трикутника через його гіпотенузу с і площу S;

2)периметр сектора через його радіус R і радіус r кола, вписаного в нього.

363°. У якій чверті тригонометричного кола лежить точка Pt,

якщо:

 

 

 

2) t = arctg (–0,4);

 

1) t = arctg 0,4;

 

 

 

3) t = arcctg 1,8;

 

4) t = arcctg (–1,6)?

 

364°. Обчисліть:

1

 

 

 

 

 

1

 

 

1)

 

 

 

2)

 

 

 

 

tg arcctg

 

 

;

tg arc tg −

 

 

;

 

 

3

 

 

 

 

 

3

 

 

3)

ctg (arc tg (−

3 ));

4)

ctg

(arcctg (−1)).

 

344

 

 

 

 

 

 

 

 

Розділ 3. Тригонометричні Функції

365°. Розв’яжіть рівняння:

 

 

 

 

 

 

 

 

1)

 

π

 

 

3

; 2)

ctg

x

= −1;

 

3)

 

 

 

tg x +

 

= −

 

 

2

 

tg2x = 3;

 

3

 

 

 

4

 

 

 

 

 

 

 

 

 

 

4)

ctg x = 3 −

2;

 

5) tg2 x

=1;

 

6)

ctg2x = 3;

 

 

 

 

 

 

 

 

2

 

 

 

 

π

7)

ctg3x = −0,3;

 

 

 

 

8)

3

+

 

 

 

 

− tg x

5

= 0;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9)(ctg x +3)(tg2x +1) = 0;

10)2sin x + π −1 (2ctg x +1) = 0.

6

366°. Знайдіть нулі функції:

1)

y = tgx +1;

2)

y =

1 tgx −

3

;

3)

y = 2ctgx +

6

.

367. Розв’яжіть рівняння:

 

2

6

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

tgπx = 3 ;

2)

x −1ctgx = 0

;

3)

tg

 

x

 

=1 .

 

 

 

 

 

 

368.Знайдіть розв’язки рівняння, які задовольняють наведену умову:

1) ctgx = −

3

,tg x

< 0 ;

2) tg2x = 0,cos x < 0 ;

3

 

2

 

 

3)tg x2 = 3,sin 3x > 0 .

369.Знайдіть найменший додатний корінь рівняння:

1)

tg(3x +75°) =1 ;

2) (ctgx +1)( 3 + tgx) = 0 ;

3)

tg(5x + 2) = 0 .

 

370*. Знайдіть розв’язки рівняння, що належать даному проміжку:

1)

tg x = −

 

 

 

 

3π

;

5π

;

 

2)

ctg 2x =1,

 

 

3π

;

 

 

 

3, x −

2

 

2

 

 

x −π;

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

x

 

π

3

 

 

 

 

 

 

 

 

4)

 

 

π

 

 

 

 

 

3π

 

π

tg

 

+

 

=

 

 

, x [0; 6π];

ctg

3x −

 

 

= −1, x

 

−

 

;

 

.

 

6

3

 

4

2

3

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

371. Розв’яжіть рівняння:

 

 

 

 

 

 

2)

 

 

 

 

 

 

 

 

 

 

 

 

1)

2sin2 x −3sin x +1 = 0;

 

 

 

4 cos2 x + sin x =1;

 

 

 

 

 

 

 

3)

ctg

2

x

−

π

 

 

 

x

−

π

 

−4 = 0;

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

+3ctg

2

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найпростіші тригонометричні рівняння і нерівності

345

 

4)

tg x +5ctg x = 6;

5)

 

2cos2 x

=1.

 

 

7cos x −3

372.

Розв’яжіть рівняння:

 

 

 

2)

 

 

 

 

1)

2 sin3 x −sin2 x = 0;

cos5x(1 + cos x) = 0;

 

3)

ctg x − cos x =1 −sin x;

4)

sin 2x tgx = 0.

373.

Розв’яжіть рівняння:

2)

 

 

 

 

1)

sin3x = cos3x;

sin2 3x = 3cos2 3x;

3)sin2 x +5sin x cos x + 4 cos2 x = 0 ;

4)3sin2 x −7sin x cos x + 6 cos2 x =1 ;

5)−4 sin2 x cos2 x −9 cos4 x = 0 ; 6) 1 −3cos2 x = sin 2x ;

7)

cos2x + cos2 x − 1 sin 2x = 0 .

 

 

 

2

 

 

374. Розв’яжіть рівняння:

2)

sin3x = sin 2x + sin x;

1)

sin 2x + sin x = 0;

3)

sin x + sin3x + cos x + cos3x = 0;

 

4)

cos x − cos2x = sin3x;

5)

sin2 x + sin2 2x =1;

6)

cos x −sin x =1;

7) 1 − cos2x = 4 sin x;

8)sin2 x + sin2 2x + sin 23x = 32 .

375.Знайдіть величину кутів ромба, якщо відношення довжин його діагоналей дорівнює 2.

Виразіть:

1)кути рівнобедреного трикутника через його основу с і площу S;

2)кути рівнобічної трапеції через її основи а і b (a > b) і площу S.

1)Висота рівнобедреного трикутника поділяється висотою, проведеною до бічної сторони, у відношенні 1:3, рахуючи від основи. Знайдіть кути трикутника.

2)Коло, вписане у рівнобедрений трикутник, проходить через точку перетину його висот (ортоцентр трикутника). Знайдіть кути трикутника.

Сума двох рівних висот рівнобедреного трикутника дорівнює третій висоті. Знайдіть кути трикутника.

У прямокутному трикутнику проекція одного з катетів на гіпотенузу вдвічі більша від другого катета. Знайдіть кути трикутника.

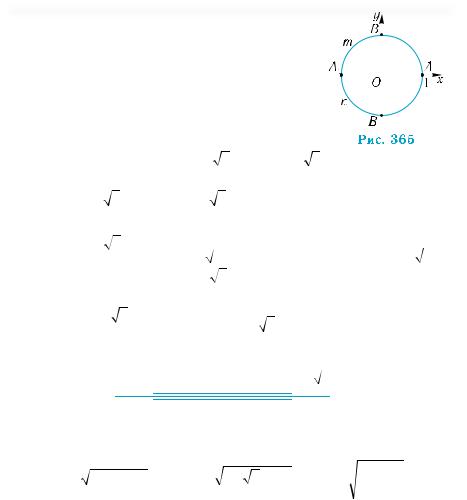
346

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 3.

 

Тригонометричні Функції

380°. Запишіть за допомогою нерівності мно-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

жину всіх чисел х (рис. 365), яким відпо-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

відають точки дуги:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

BmA1;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2)

A1nB1;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

BA1B1;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4)

A1B1A.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

381°. Розв’яжіть нерівність:

 

 

 

2

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

sin x >

1

;

 

2) sin x ≥ −

 

 

; 3)

sin x <

 

 

;

 

 

4 )

 

sin x ≤ −

1

;

 

 

2

 

2

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5)

cos x ≥

 

 

 

3

;

6)cos x > −

 

 

2

; 7)

cos x <

1

;

 

 

 

 

8 )

 

cos x ≤ −

1

;

 

 

2

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9)

tg x ≥ −

3 ;

10) tg x >

 

1

 

 

;

11) tg x ≤1;

 

 

 

 

12) tg x < −

1

 

;

 

 

3

 

 

 

 

 

 

 

 

13) ctg x > −1;

14) ctg x <

 

 

 

15) sinx < 0.

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

3;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

382.

Розв’яжіть нерівність:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1)

sin 2x >

 

2

;

 

 

 

 

 

 

 

 

2)

 

 

 

 

 

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 sin x −

 

 

 

>

1;

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3)

 

x

 

 

 

 

 

 

 

 

 

 

 

 

4)

 

2x

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

tg −

2

< −1;

 

 

 

 

 

 

 

 

ctg

3

>

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

383.

Розв’яжіть рівняння:

 

 

 

 

 

 

 

 

 

 

3) tg x = |tg x|.

 

 

 

 

 

 

 

1) cos x

=

 

|cos x|;

2) |sin x| = –sin x;

 

 

 

 

 

 

 

384. Знайдіть область визначення функції:

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

1)

y =

2sin x +1;

2) y =

 

1 − 2 cos x;

3)

 

y =

.

 

 

 

 

 

 

 

 

1 + tg x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

385*. Точка

здійснює

гармонічні

коливання

за законом

 

y

 

 

 

π

t −

π

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= 6sin

3

. В які проміжки часу вона буде віддалена

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

від точки рівноваги на відстань, що не перевищує 3?

 

 

 

 

 

 

386*. 1) У круговий сектор вписано коло. Яким має бути центральний кут сектора α, щоб радіус вписаного кола не перевищував третини радіуса сектора?

2) Яким має бути більший гострий кут α прямокутного трикутника, щоб довжина гіпотенузи більше ніж удвічі перевищувала довжину меншого з катетів?

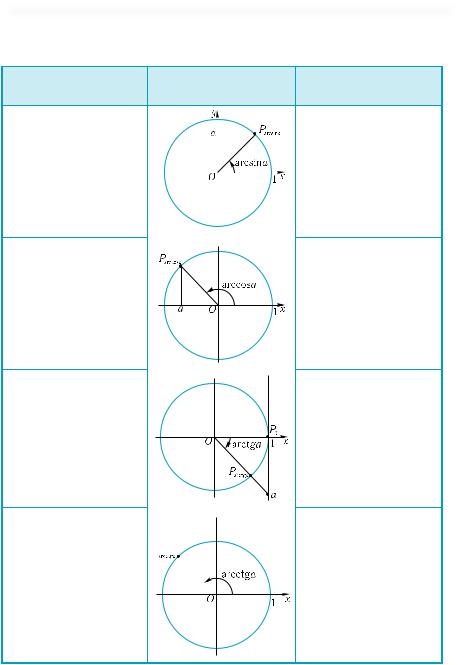
Найпростіші тригонометричні рівняння і нерівності

347

 

 

 

 

Підсумок

 

 

 

 

 

Основні поняття

 

 

Означення

 

Геометрична

Застосування

 

 

ілюстрація

 

 

 

 

 

Арксинус

числа

 

 

 

sin х = а, –1 ≤ а ≤ 1.

 

а [–1; 1] — таке чис-

 

 

 

х = (–1)karcsin a + πk,

 

 

 

 

ло

α, що: sin α

= а;

 

 

 

k Z.

π

π

 

 

 

 

 

 

 

 

− 2

≤ α ≤ 2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Арккосинус числа

a [–1; 1] — таке число α з відрізка

[0; π], що cos α = a.

Арктангенс числа а — таке число α,

що: tg α = a ;

− 2π < α < 2π.

Арккотангенс числа а — таке число α, що: ctg α = а; 0 < α < π.

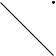
cos х = а, –1 ≤ а ≤ 1. х = ±arccos a + 2πk,

k Z.

tg х = а.

х = arctg a + πk, k Z.

ctg х = а.

х = arcctg a + πk, k Z.

1

готуємось до тематичного

 

оцінювання з теми

 

«Тригонометричні

 

функції»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

?

Завдання для самоконтролю

 

 

 

 

 

 

1.

У якій чверті міститься точка Pt, якщо t дорівнює:

 

 

а)

2π

;

б)

8π

;

 

в) 4;

 

г) −17π;

ґ) 5,7 π?

 

 

 

9

 

2.

9

 

 

 

 

 

 

 

 

 

 

 

 

9

 

 

Яким числам з проміжку (0; 3π) на тригонометричному колі

 

 

відповідає точка Pt з:

 

 

 

 

б) абсцисою 0; 1; –1?

 

 

а) ординатою 0; 1; –1;

 

 

 

 

3.

Чому дорівнюють координати точки Pt

на тригонометричному

 

 

колі, якщо t

дорівнює:

 

 

 

3π

 

 

 

 

 

 

 

ґ) − π ?

 

 

а) 0;

б)

π;

 

в)

;

г) π;

 

 

 

 

 

 

 

4.

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

2

 

На який кут повернеться за 5 с точка на околі колеса машини

 

 

при рівномірному русі, якщо за 2 с колесо робить 6 обертів?

5.

Скільки існує точок Pt

 

на тригонометричному колі, якщо для

 

 

відповідних значень t:

= 0,7;

 

в) sin t = –1;

 

 

г) cos t = –0,6?

 

 

а) cos t = 1;

 

б) sin t

 

 

 

6.

На який кут слід повернути хвилинну стрілку годинника, щоб

 

 

перевести годинник вперед:

в) на 1 год;

 

 

г)на2год40хв?

 

 

а) на 10 хв;

 

б) на 20 хв;

 

 

7.

Якізнакимаютьсинус,косинус,тангенсчислаt,якщоt дорівнює:

 

 

а) 3;

 

 

б)

 

16π

;

 

 

 

в) 7?

 

8.

 

 

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Які з наведених далі точок належать тригонометричному колу:

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

 

 

а) А(0,3; 0,7);

б) В(–0,8; –0,6);в) C

 

 

; −

 

 

 

; г) E(0; 0)?

 

 

5

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Готуємось до тематичного оцінювання з теми«Тригонометричні функції»

349

9.Чи можуть синус і косинус того самого аргументу одночасно дорівнювати:

а)

3

і

4

;

б) 1 і 0;

в) 0,9 і 0,1;

г) −

1

і −

2

?

5

5

3

3

 

 

 

 

 

 

 

 

10.Чи можуть тангенс і котангенс того самого аргументу дорівнювати:

 

а)

1 і 2;

б) 0,6 і 0,8;

в)

 

2 +1 і

 

2 −1 ;

г) 5 і −1 ?

11.

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

Які з наведених функцій є парними; непарними; ні парними,

 

ні непарними:

 

 

б)

y = x + cos x;

 

 

 

 

в) у = x2 cos x;

 

а)

y = cos x ;

 

 

 

 

 

 

 

г)

y = sin2 x;

 

 

ґ)

y = sin x cos x;

 

 

 

д)

y = sin x + cos x ?

12.

Зростаючою чи спадною є функція y = sin x на проміжку:

 

а)

3π

 

 

 

 

 

б)

[2; 3];

 

 

 

 

 

 

в)

 

π

;

3π

 

 

 

; 2π ;

 

 

 

 

 

 

 

 

 

2

 

;

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

г)

[0; π];

 

 

ґ) [0; 1];

 

 

 

 

 

 

д)

[π; 2π]?

13.

Що більше:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а)

sin

 

π

чи sin

4π

;

 

б)

cos

2π

чи

cos

π

;

 

9

 

 

 

 

3

 

в)

 

 

чи sin2

9

 

 

г)

 

 

9

чи

 

 

 

 

 

 

sin1

;

 

 

cos2

cos3 ?

 

14.

Які з поданих чисел є періодами функції

y = cos x :

 

а) π;

 

 

 

 

 

 

б) 2π;

 

в) 3π;

 

 

 

 

 

г)

π;

 

ґ) 4π;

 

 

 

 

 

 

д) 5π;

 

е) 6π?

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.

Чому

 

дорівнює на проміжку

 

π

;

π

 

найбільше значення

 

 

4

 

 

 

 

функції:

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

б)

y = ctgx ?

 

 

 

 

 

 

а)

y = tgx ;

 

 

 

 

 

 

 

 

 

16.

Яке з чисел більше:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а)

tg

3π

 

чи tg

3π

;

 

б)

ctg

π

чи ctg

π ?

 

 

 

 

 

4

 

17.

 

5

 

8

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

Який найменший додатний період має функція:

 

 

а)

y = sin3x ;

б) y = cos x ;

в)

y = tg x ;

 

 

 

г)

y = ctg2x ?

18.

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

3

 

 

 

 

 

 

Знайдіть множину значень функції:

 

 

 

 

 

 

 

 

 

а)

y =

 

1 cos2x ;

 

 

б)

y = cos x −2;

 

 

 

 

в)

y = cos(1 − x).

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

350

Розділ 3. Тригонометричні Функції

19.Якого найбільшого і якого найменшого значень набуває функція:

 

а) y = 2cos π −3x ;

 

б)

y = 3sin x + π ?

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

4

 

 

 

 

 

 

 

 

 

20.

Відомо, що sin25° = a. Чому дорівнює sin50°?

 

 

 

21.

Чи може не мати розв’язків рівняння:

 

 

 

 

 

 

 

а) sin x = a;

 

 

б) cos x = a?

 

 

 

 

 

 

Скільки розв’язків на проміжку [0; 7π] має рівняння:

 

 

 

а) sin x = 1 ;

б) sin x = −

2

; в)

cos x =

2

;

г) cos x = −

3

?

 

2

2

2

 

2

 

 

 

 

 

 

 

23.Яких із наступних значень: −23π; − 2π; − 3π; −1; 0; 5; 23π; 34π; 56π;

76π; 4 не може набувати arccosa ?

24.Яких із наступних значень: − 6π; − 4π; 0; 6π; 4π; 3π; 79π; 23π; 34π;3,2;

3,5; 56π; π не може набувати arcctga ?

25.Чому дорівнює:

 

а) cos arccos −

1 ;

 

 

 

 

 

 

 

 

2

 

2

 

 

 

б) sin arcsin

+ arccos −

 

?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

26.

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

Які з наведених нижче рівнянь є однорідними відносно sin x

 

і сos x:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a)

sin x +3cos x = 0;

б) sin x + cos x =1;

 

 

 

 

в)

sin2 x + 2cos x −3cos2 x = 0;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

2sin2 x +3sin x cos x −5cos2 x = 0;

 

 

 

 

 

 

 

 

 

ґ)

sin2 x + cos2 2x = 0;

д)

 

2sin2 x −3sin x cos x = 0?

 

 

27.

Чи має розв’язки нерівність:

 

 

 

 

 

 

 

в) sin x > 1?

 

 

 

 

а) cos x

< 1;

б) sin x ≥ 1;

 

 

 

 

 

 

 

 

 

28.

Знайдіть усі розв’язки нерівності:

 

 

 

 

г) sin x ≥ 1.

 

 

 

а) cos x ≤ –1;

б) cos x ≥ 1;

в) sin x ≤ –1;

 

 

29.

Знайдіть усі розв’язки нерівності:

 

 

 

 

 

 

 

 

 

а)

 

−1 ≤ sin x ≤1;

 

б)

−1 < cosx <1.

 

 

 

30.

При яких значеннях х виконується рівність:

 

 

 

 

 

а)

 

cos x

 

= cos x ;

б)

 

 

 

sin x +1

 

= −sin x −1 ;

 

 

 

 

 

 

 

 

 

 

 

 

в)

 

cos x −1

 

= cos x −1 ;

г)

 

sin x

 

 

= −sin x ?

 

 

 

 

 

 

 

 

 

 

 

31.

При яких значеннях х має зміст вираз

sin 2x −1 ?

 

 

 

Готуємось до тематичного оцінювання з теми«Тригонометричні функції»

351

Відповіді до завдань для самоконтролю

1. а) У першій; б) у другій; в) у третій; г) у першій; ґ) у четвертій. 2. а) π, 2π,

π2 , 52π ; 32π; б) π2 , 32π ; 52π, 2π, π. 3. а) (1; 0); б) (0; 1); в) (0; – 1); г) (–1; 0); ґ) (0; – 1).

4. 5400°. 5. а) 1; б) 2; в) 1; г) 2. 6. а) 60°; б) 120°; в) 360°; г) 960°. 7. а) +, –, –; б) –, +, –; в) +, +, +. 8. В, С, D. 9. а) Так; б) так; в) ні; г) так. 10. а) Так; б) ні; в) так;

г) ні. 11. Парні: а), в) г); непарна: ґ); ані парні, ані непарні: б), д). 12. а) Зрос-

таюча; б) спадна; в) спадна; г) не є монотонною; ґ) зростаюча; д) не є монотон-

ною. 13. а)

sin

4π

; б)

 

cos

2π

; в) sin 2; г) cos 2. 14. б), д), е). 15. а) Не існує; б) 1.

 

 

 

 

 

3π

 

 

 

9

 

π

 

9

 

2π

 

 

π

 

 

 

1

 

1

 

 

16. а)

tg

;

б)

ctg

.

17. а)

;

б) 4π; в) 3π; г)

. 18. а)

 

−

;

;

б) [–3; –1];

8

5

3

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

в) [–1; 1]. 19. а) 2 і –2; б) 3 і –3. 20. 2a 1 − a2 .

21. а) Так; б) так. 22. а) 8; б) 6;

в) 7; г) 7. 23. − 2π; − π

; − π; −1;

7π ,4.

24.

−

π

; −

π; 3,2; 3,5; π. 25. а) −1 ; б) 0.

 

3

2

3

 

6

 

 

 

 

6

 

4

 

б)

2

26. а), г), д). 27. а) Так; б) так; в)

ні. 28. а)

π + 2πn,n Z;

2πn,n Z;

в)

− π + 2πn,n Z;

г)

π + 2πn,n Z.

29.

а)

х

R; б)

x (2πn; π + 2πn)

 

2

 

2

 

 

 

π

 

 

 

 

 

 

 

π

 

(π + 2πn;2π + 2πn),n Z. 30.а) x

 

+

2πn;

π

+

 

 

x = −

+ 2πn,n Z;

−

2

2

2πn ,n Z ;б)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) х = 2πn,n Z ; г) x π + 2πn; 2π + 2πn ,n Z . 31. π + πn,n Z.

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

1.

 

Зразок контрольної роботи №3

 

 

 

Дано функцію

y = f(x),

де

f(x) = 2cos(2π − x) .

 

 

 

 

1°) З’ясуйте, чи є функція

y = f(x)

парною або непарною.

 

2°) Чи є функція y = f(x)

періодичною? Якщо так, то знайдіть

 

її основний період.

 

 

 

 

 

 

 

 

 

 

 

 

3°) Побудуйте її графік на проміжку [–π; π].

 

 

 

 

4) Знайдіть множину значень функції y = f(x) .

 

 

 

5) Знайдітькоординатиточокперетинуграфікафункції y = f(x) :

 

а°) з прямою x =

2π

;

 

 

 

б) з прямою у = –1.

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

2.Дано рівняння: sin2x = 22 . а°) Розв’яжіть його.

б°) Знайдіть його найменший додатний корінь.

в) Знайдіть ті його розв’язки, які належать проміжку [2π; 3π]. г) Знайдіть ті його розв’язки, які задовольняють умову: tgx ≤ 0. ґ) При яких значеннях х функція y = sin2x набуває значень, менших від 22 ?

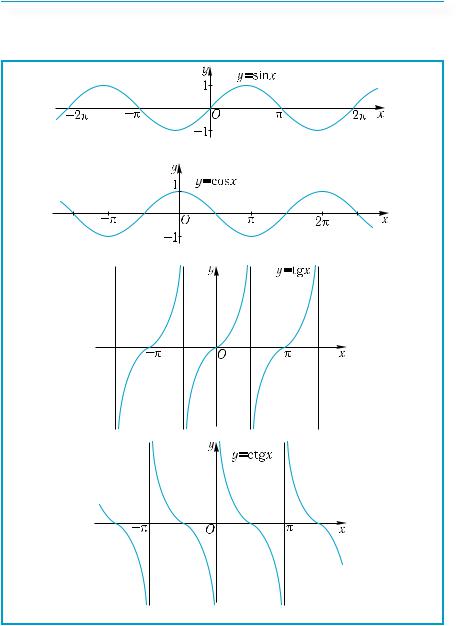
352

Розділ 3. Тригонометричні Функції

Графіки тригонометричних функцій

Таблиця 32

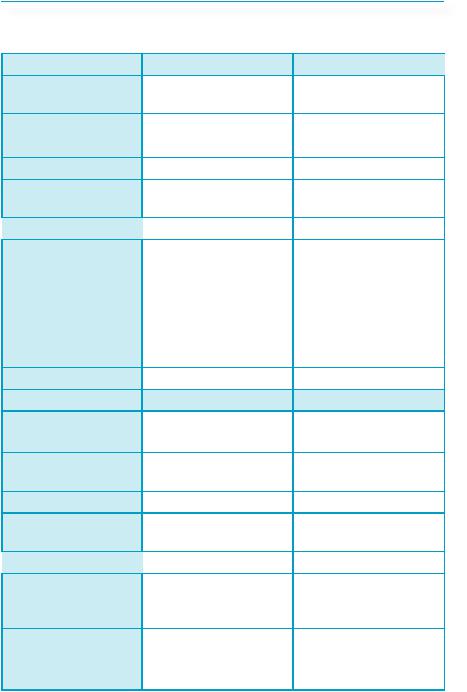
Готуємось до тематичного оцінювання з теми«Тригонометричні функції»

353

Властивості тригонометричних функцій

Область

визначення

Нулі

Основний період

Парність і непарність

Множина значень

Найбільше і найменше значення

Неперервність

Область

визначення

Нулі

Основний період

Парність і непарність

Множина значень

Найбільше і найменше значення

Неперервність

y = sin x R

πn, n Z

2π

Непарна

[–1; 1]

унайб = 1 при

х = 2π + 2πk

унайм = –1 при

х = – 2π + 2πk ,

k Z

Неперервна y = tg x

x ≠ 2π + πk , k Z

πn, n Z

π

Непарна

Таблиця 33 y = cos x

R

2π + πn,n Z

2π

Парна

[–1; 1]

унайб = 1 при

x = 2πk

унайм = –1 при

x = π(2k +1) , k Z

Неперервна y = ctgx

x ≠ πk , k Z

2π + πn,n Z

π

Непарна

R

R

Найбільше і най-

Найбільше і най-

менше значення не

менше значення не

існують

існують

π

x = πk , k Z — точ-

x = 2 + πk , k Z —

ки розриву

точки розриву

 

23 Математика, 10 кл.

354

 

 

 

 

 

 

 

 

 

 

 

Розділ 3. Тригонометричні Функції

 

 

 

 

 

Деякі тригонометричні формули

 

Таблиця 34

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Множина зна-

Множина зна-

 

 

 

 

 

 

 

 

 

 

 

чень

 

 

 

 

 

 

 

 

 

 

 

 

 

 

чень

№

 

 

 

 

 

 

 

 

 

аргументів, за

 

 

 

Формула

аргументів, за

п/п

яких має

 

 

 

 

 

 

 

 

 

яких має зміст

 

 

 

 

 

 

 

 

 

 

зміст ліва час-

 

 

 

 

 

 

 

 

 

 

права частина

 

 

 

 

 

 

 

 

 

 

 

тина

 

 

 

 

1 tg α =

 

1

 

 

 

 

 

α ≠ π + kπ, k Z

α ≠

π k, k Z

ctg α

 

 

2

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

α ≠

π

+ kπ, k Z

 

 

 

 

 

 

 

tg α + tg β

 

π

 

 

2

 

 

2

tg (α + β) =

 

 

α + β ≠

+ kπ, k Z

β ≠

π

+ kπ, k Z

1 − tg αtg β

2

 

 

 

 

 

 

 

 

2

 

π + kπ, k Z

 

 

 

 

 

 

 

 

 

 

 

 

 

α + β ≠

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

α ≠

π

+ kπ, k Z

 

 

 

 

 

 

 

tg α − tg β

 

π

 

 

2

 

 

3 tg (α − β) =

 

 

α − β ≠

+ kπ, k Z

β ≠

π

+ kπ, k Z

1 + tg αtg β

2

2

 

 

 

 

 

 

 

 

 

π + kπ, k Z

 

 

 

 

 

 

 

 

 

 

 

 

 

α − β ≠

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

2tg α

π π

 

α ≠

π

+ kπ, k Z

 

 

 

 

 

2

4

tg 2α =

 

 

 

 

α ≠ 4 +

2 k, k Z

 

 

 

 

1 − tg2 α

α ≠ ±

π

+ kπ, k Z

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2tg α

 

 

 

 

 

 

 

5

sin α =

 

 

2

 

 

α R

 

 

α ≠ π + 2kπ, k Z

1 + tg2 α

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

1 − tg2 α

 

 

 

 

 

 

 

6

cos α =

 

 

2

 

 

α R

 

 

α ≠ π + 2kπ, k Z

1 + tg2 α

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

Готуємось до тематичного оцінювання з теми«Тригонометричні функції»

355

Розв’язання найпростіших тригонометричних рівнянь

 

 

Таблиця 35

Тип рівняння

Розв’язок

 

sin x = a

sin x = 0

sin х = 1

sin х = –1 cos х = а

cos х = 0

cos х = 1 cos х = –1 tg х = а ctg х = а

Якщо |а| > 1, то рівняння не має розв’язків.

Якщо |а| ≤ 1, то x = (−1)k arcsina + πk, k Z.

Окремі випадки

x = πn, n Z

x = 2π + 2πn, n Z x = − 2π + 2πn, n Z

Якщо |а| > 1, то рівняння не має розв’язків.

Якщо |а| ≤ 1, то х = ± arccos а + 2πп, п Z.

Окремі випадки

x = 2π + πn, n Z x = 2πn, n Z

x= π + 2πn, n Z

х= arctg а + πп, п Z

х = arcctg а + πп, п Z

23*

356

 

 

Розділ 3. Тригонометричні Функції

Зміст чисел arcsin a, arccos a, arctg a, arcctg a

 

 

 

Таблиця 36

Число

 

 

Зміст

х = arcsin a

1)

π

π

 

− 2

≤ x ≤ 2 ; 2) sin x = a.

х = arccos a

1)

0 ≤ х ≤ π; 2) cos х = a.

х = arctg а

 

π

π

1) − 2

< x < 2 ; 2) tg x = a.

 

х = arcctg а

1)

0 < x < π; 2) ctg х= а.

Розділ 4.

Перпендикулярність прямих і площин

У розділі «Паралельність прямих і площин» розглянуто різні випадки взаємного розміщення прямих і площин у просторі. Зокрема, грунтовно вивчалось відношення паралельності. Однак численні застосування геометрії пов’язані, насамперед, з вимірюванням геометричних величин (від-

станей, кутів тощо). Предметом багатьох вимірювань є прямі та площини, які перетинаються. Тому необхідно більш детально дослідити взаємне розміщення прямих і площин, виявити величини, які характеризують це розміщення.

Окремим випадком розміщення прямої і площини, що мають одну спільну точку, є перпендикулярність, яка моделює відношення вертикальності між фізичними тілами та інші подібні відношення (наприклад, цвях, забитий у стіну). Скориставшись поняттям перпендикулярності, ми зможемо вимірювати відстань від точки до площини, від прямої до паралельної їй площини, відстань між паралельними площинами. На цих вимірюваннях ґрунтується вимірювання відстані між довільними реальними об’єктами.

He менш важливим є введения кількісних характеристик взаємного розміщення прямих і площин, що перетинаються, — кута між прямою і площиною, кута між площинами. Ці поняття споріднені з планіметричним поняттям кута між прямими (та й визначаються за його допомогою).

Готуємось до вивчення

теми «Перпендикулярність прямих і площин»

Таблиця 37

Прямокутний трикутник

Теорема Піфагора і співвідношення між сторонами і кутами прямокутного

трикутника c2 = a2 +b2 , sin A = ac = cos B ,

sin B = bc = cos A , tg A = ab , tg B = ab .

Метричні співвідношення у прямокутному трикутнику

Висота, опущена на гіпотенузу пря- мокутного трикутника, поділяє цей трикутник на два подібних даному і подібних між собою трикутники.

Таблиця 38

Вписане та описане коло

Навколобудь-якоготрикутникамож- на описати коло і при цьому лише одне. Центр описаного кола збігається з точкою перетину серединних перпендикулярів до сторін трикутника.

У будь-який трикутник можна вписати коло і при цьому лише одне. Центр вписаного кола лежить на перетині бісектрис кутів трикутника.

Готуємось до вивчення теми «Перпендикулярність прямих і площин»

359

Таблиця 39

Паралельність прямих і площин

Для встановлення паралельності двох прямих у просторі достатньо перевірити:

чи знайдеться пряма, паралельна кож- ній із даних прямих;

чи будуть дані прямі лініями перетину двох паралельних площин третьою.

Для встановлення мимобіжності двох прямих у просторі достатньо перевірити:

чи знайдеться площина, в якій лежить одна з даних прямих і яку перетинає друга пряма у точці, що не належить першій прямій.

Длявстановленняпаралельностіпрямої,щонележитьу даній площині, і цієї площинидостатньоперевірити:

чи знайдеться в площині пряма, па- ралельна даній прямій.

Для встановлення паралельності двох площин достатньо перевірити:

чи знайдуться в одній із площин дві пря- мі, що перетинаються і відповідно пара- лельні двом прямим другої площини;

чи знайдеться площина, паралельна кож­ ній із даних площин.

тест для діагностики

готовності до вивчення теми «Перпендикулярність прямих і площин»

1.

Пряма AB не належить площині COD.

 

Скільки спільних точок мають площини

 

AOB і COD, зображені на рисунку?

 

А. Одну.

Б.

Дві.

В. Безліч.

 

Г. Відповідь відрізняється від наведених.

2.

Перетином площин

AED

і AFB, зображе­

 

них на рисунку, є …

відрізок АС;

 

А. точка А;

Б.

 

В. сукупність двох точок {A; C};

 

Г. пряма АС.

 

 

 

3.На зображенні тетраедра в одній грані не ле­ жать точки …

іY; Б. X і Z;

іT; Г. Z і T.

4.

Два прямокутники ABCD і AEFD лежать у

 

 

різних площинах. Прямі ВС і EF …

 

 

А. перетинаються;

Б. паралельні;

 

 

В. мимобіжні;

 

 

 

 

 

 

Г. можуть бути розміщені по­різному в за­

 

 

лежності від розміщення площин.

 

 

5.

Проекцією двох паралельних прямих не може бути …

 

А. одна пряма; Б. одна точка;

В. дві прямі;

Г. дві точки.

6.

Проекцією квадрата не може бути …

 

 

А. відрізок;

 

 

Б.

ромб;

 

 

В. прямокутник;

 

 

Г.

трапеція.

 

7.

Якщо d — довжина відрізка, d1 — довжина його паралельної

 

проекції на площину, то …

 

 

 

 

А. d > d1;

Б. d < d1;

 

В. d = d1;

 

Г. жодне з наведених співвідношень не є правильним.

Тест для діагностики готовності до вивчення теми

361

8.

Скільки існує площин,

паралельних ребру­

 

 

 

ВВ1 куба ABCDA1B1C1D1

і таких, що прохо-

 

 

 

дять через вершину D?

 

 

 

 

 

 

 

 

 

А. Жодної.

Б. Одна.

 

 

 

 

 

 

 

В. Дві.

Г. Безліч.

 

 

 

 

 

 

 

 

 

 

 

9.

Скільки площин можна провести через вершину трикутника,

 

паралельних його стороні, що не містить цю вершину?

 

А. Жодної.

 

 

Б.

Одну.

 

В. Безліч.

D, E, F,

Г.

Не більш однієї.

10.

На рисунку точки

G — середини

 

ребер AS, SC, BC,

AB. Знайдіть периметр

 

чотирикутника DEFG, якщо DG

=

4 см,

 

АС = 16 см.

Б. 16 см.

 

 

 

 

 

 

 

А. 24 см.

 

 

 

 

 

 

 

В. 32 см.

Г. 40 см.

 

 

 

 

 

 

11.

Відомо, що прямі а і b паралельні площині a. Як розміщені

 

прямі а і b?

Б. Перетинаються.

 

А. Паралельні.

 

В. Збігаються.

Г. Можуть бути розміщені по-різному.

12.

Якщо діагоналі трапеції паралельні площині a, то основи

 

трапеції …

 

 

Б. паралельні a;

 

А. лежать у площині a;

 

 

В. перетинають a;

 

 

 

 

 

 

 

 

 

 

Г. можуть перетинати a, а можуть і бути їй паралельними.

13.

Якщо лінії перетину площин a і β

площиною γ паралельні, то

 

площини a і β …

 

 

Б. перетинаються;

 

А. паралельні;

 

 

 

В. паралельні чи збігаються;

 

 

 

 

 

 

 

Г. можуть бути паралельними або перетинатися.

14.

Периметр многокутника, отриманого в перерізі

 

кубаABCDA1B1C1D1

зребром

аплощиною,щопро-

 

 

 

 

 

ходить через середини ребер

АВ і ВС

паралельно

 

 

 

 

 

ребру DD1, дорівнює …

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

А. 2а;

Б. 2 2a ;

 

 

 

 

 

 

 

B. 2(a + 2a) ;

Г. 2a + 2a .

 

 

 

 

 

15.

Перерізом правильного тетраедра площиною не може бути …

 

А. трапеція;

Б. рівносторонній трикутник;

 

В. ромб;

Г. правильний шестикутник.
Соседние файлы в предмете Аналитическая геометрия
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности