
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач

§10. Зображення фігур у стереометрії
Розглядаються особливості побудови зображень фігур, насамперед плоских, задачі на побудову на зображеннях.
При вивченні питання про зображення фігур у сте- 
 реометрії основну увагу зосередимо на зображенні
реометрії основну увагу зосередимо на зображенні  плоских фігур. І це зрозуміло, оскільки дивлячись на реальний фізичний об’єкт (будинок, гральний кубик, книжку та ін.), ми бачимо поверхню, яка у багатьох випадках складається з плоских частин (рис. 201 – 203). На рисунках і технічних кресленнях передусім намагаються зобразити поверхню об’єкта, а наш життєвий досвід дає змогу за деталями поверхні побачити предмет у цілому.
плоских фігур. І це зрозуміло, оскільки дивлячись на реальний фізичний об’єкт (будинок, гральний кубик, книжку та ін.), ми бачимо поверхню, яка у багатьох випадках складається з плоских частин (рис. 201 – 203). На рисунках і технічних кресленнях передусім намагаються зобразити поверхню об’єкта, а наш життєвий досвід дає змогу за деталями поверхні побачити предмет у цілому.
Оскільки основна плоска фігура — це трикутник, з’ясуємо, яка фігура може бути зображенням трикутника. А відтак ми зможемо обговорити питання про зображення інших многокутників, відомих з планіметрії. Крім того, мова йтиме і про зображення найпростіших просторових фігур.
За геометричну основу зображення візьмемо паралельне проектування. Передусім треба уточнити зміст поняття «зображення», адже розуміти під зображенням фігури безпосередньо її паралельну проекцію — доволі незручно. Фігуру великих розмірів
12*
180 |
Розділ 2. Паралельність прямих і площин |
просто неможливо спроектувати на аркуш паперу — для того, щоб зображення помістилося, паралельну проекцію фігури потрібно пропорційно зменшити (або збільшити в інших ситуаціях).
Зображенням просторової фігури називається фігура, яка подібна паралельній проекції даної фігури на деяку площину.
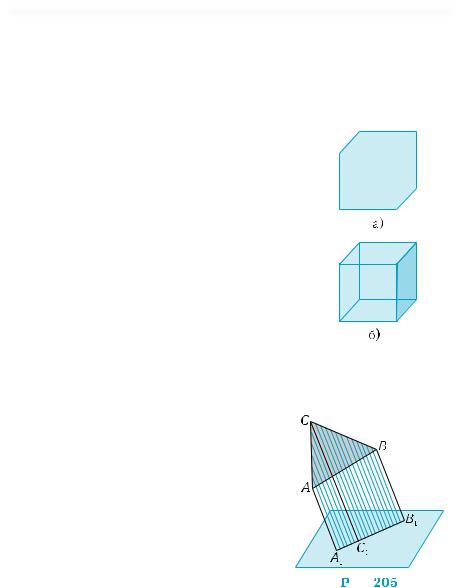
Дане означення вимагає доповнення. Зрозуміло, що зображення повинно містити якомога більше інформації про фігуру. Навряд чи паралельна проекція куба на рис 204, а) доволі повно відображає особливості цієї фігури. Тому на зображенні многогранників зображають їхні вершини і ребра, видимі й невидимі. Як вже зазначалося, невидимі лінії зображають штриховими лініями. Таким чином, зображення куба на рис. 204, б) більш повно дає інформацію про куб.
На зображенні просторової фігури виділяютьтакожзображенняїїважливихелементів
(наприклад, діагоналей, перерізів тощо). 


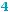 Зазначимо, що в означенні не фіксується ні площина проекцій,
Зазначимо, що в означенні не фіксується ні площина проекцій,
ні напрям проектування. Це і зрозуміло, оскільки зручну для розгляду позицію можна обирати вільно.
Тепер відповімо на запитання: яка фігура може бути зображенням трикутника? Випадок, коли трикутник лежить у проектуючій площині, не розглядатимемо. У цьому разі він проектується на відрізок
(рис. 205).
Оскільки паралельною проекцією трикутника є трикутник (окрім зазначеного вище випадку), то і зображенням трикутника має бути трикутник. Водночас вини-
кає запитання: «А який трикутник можна 
 вважати зображенням даного трикутника?». Як відомо, при па-
вважати зображенням даного трикутника?». Як відомо, при па-
ралельному проектуванні змінюються довжини відрізків, міри кутів. Зрозуміло, що паралельною проекцією рівнобедреного трикутника є, взагалі кажучи, різносторонній трикутник, проекцією тупокутного трикутника може бути гострокутний і т. д.

Зображення фігур у стереометрії |
181 |
Проведення простих експериментів з картонними моделями трикутників при отриманні їхньої тіні від Сонця чи від віддаленої лампи показує, що форма паралельних проекцій трикутника може бути різною. Більше того, можна переконатись у тому, що за рахунок відповідного розміщення моделі можна отримати як проекцію трикутник заданої форми. Таким чином, розглядаючи різні тіні одного трикутника, можна дійти наступного висновку.
Зображенням даного трикутника може бути довільний трикутник.
Математичне обґрунтування цього факту буде зроблено нижче. Користуючись ним, можна зробити певні висновки щодо зображення деяких чотирикутників.
Із властивостей паралельного проекту- 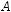 вання випливає, що зображенням паралелограма є довільний паралелограм. Справді, паралелограм діагоналлю розбивається
вання випливає, що зображенням паралелограма є довільний паралелограм. Справді, паралелограм діагоналлю розбивається
на два рівні трикутники (рис. 206, а). Зображенням трикутника ABD може бути
довільний трикутник A1B1D1. Добудувавши трикутник A1B1D1 до паралелограма (рис. 206, б), який однозначно визначається цим трикутником, отримаємо наступний висновок.
Зображенням даного паралелограма може бути довільний паралелограм.
Щодо трапецій, то подібного висновку про їхні зображення зробити не можна, оскільки при паралельному проектуванні має зберігатись відношення довжин паралельних основ. Якщо, наприклад, одна з основ удвічі менша від другої, то і на зображенні це співвідношення має зберігатись. Хоча, звичайно, зображенням трапеції має бути трапеція (але не довільна!).
Щодо зображення інших многокутників, то можна вибрати три їхні точки, що не лежать на одній прямій (наприклад, три вершини). Ці точки визначають трикутник, який може зображатись довільним трикутником. Далі, користуючись властивостями паралельного проектування (вони є і властивостями зображень),
182 |
Розділ 2. Паралельність прямих і площин |
можна у деяких випадках будувати зображення всього многокутника.
Навчившись зображати деякі плоскі фігури, розміщені у просторі, можемо приступити до зображення найпростіших просторових фігур.
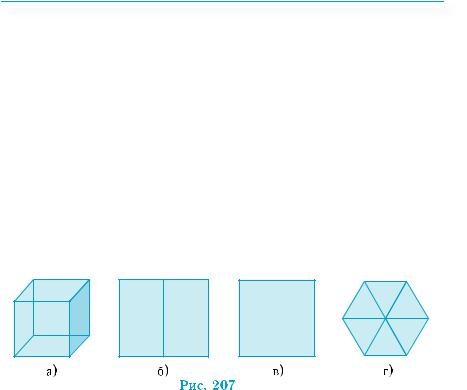
Зображення прямокутного паралелепіпеда чи куба нічим не відрізняються від зображень довільного паралелепіпеда, бо зображеннямиквадратівтапрямокутниківможутьбутидовільніпаралелограми. Найчастіше куб зображають так, як це зроблено на рис. 207, а). На рис. 207, б–г) теж подано зображення куба. Однак, на відміну від рис. 207, а), за цими зображеннями важко скласти уявлення про властивості куба. На рис. 207, б), в) зображення прості й правильні, тобто виконані за законами паралельного проектування. Проте вони не є наочними. Сказане не означає, що у деяких випадках нам
не знадобиться кожне з наведених зображень.
Розглянемо докладніше побудову зображення паралелепіпеда. У §8 паралелепіпед розглядався як многогранник, гранями якого є шість паралелограмів. У тому самому параграфі розглядався підхід до побудови фігур з відрізків. Скористаємось ним.
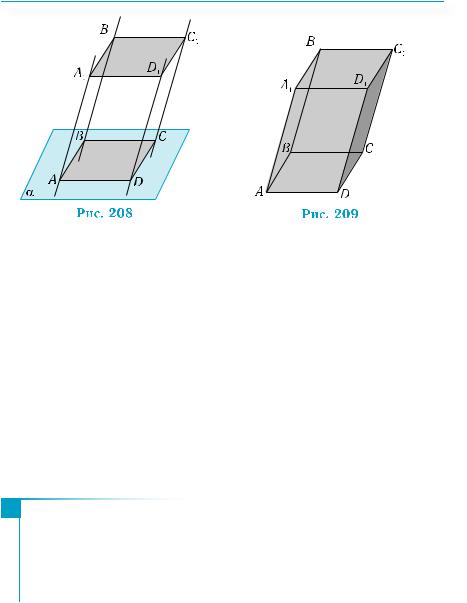
У даній площині α побудуємо паралелограм ABCD і через усі його вершини проведемо паралельні прямі, які перетинають площину α (рис. 208). На цих прямих по один бік від площини α відкладемо відрізки АА1, ВВ1, СС1, DD1 однакової довжини. Неважко довести, що точки А1, В1, С1, D1 лежать в одній площині і є вершинами паралелограма A1B1C1D1. Справді, оскільки AA1D1D, ABCD і ВВ1С1С — паралелограми, то A1D1 || AD, AD || ВС, ВС || В1С1 і, згідно з ознакою паралельності прямих (теорема 2 §8), A1D1 || В1С1. Це, зокрема, дає нам змогу стверджувати, що точки A1, B1, C1, D1 лежать у одній площині.
Аналогічно маємо, що А1В1 || D1C1, тобто чотирикутник А1В1С1D1 є паралелограмом.
Зображення фігур у стереометрії |
183 |
Сукупність усіх точок відрізків, що сполучають точки паралелограмів ABCD і А1В1С1D1, утворюють фігуру, яка є паралелепіпедом (рис. 209). Зрозуміло, що під час побудови паралелепіпедів можна обійтись паралельними відрізками, що сполучають відповідні точки паралелограмів. Зображення виконано, як і на рис. 208, тільки з урахуванням того, що паралелепіпед «заповнений» точками, і деякі лінії невидимі для спостерігача. Як і в кресленні, їх зображають штриховими лініями. Позначають паралелепіпед за його вершинами: ABCDA1B1C1D1.
Дві грані паралелепіпеда, що мають спільне ребро, називаються суміжними, а ті, що не мають спільних ребер,— протилежними. Дві вершини, які не належать до однієї грані, називаються протилежними. Відрізок, що сполучає протилежні вершини,
називається діагоналлю паралелепіпеда.
Зображення пірамід, зокрема тетраедрів, було розглянуто у §8 у зв’язку з їхньою побудовою з відрізків.
! Розгляд зображень плоских і просторових фігур дозво-
ляє сформулювати вимоги до зображень:
1) зображення має бути правильним, тобто задовольняти певні правила; 2) зображення має бути наочним;
3) зображення має бути простим для виконання.
Правильністьзображеннязабезпечуєтьсядотриманнямправил побудови паралельних проекцій. Наочність і простота забезпечуються вибором напрямку проектування, тобто «кута зору» на фігуру та розміщенням площини проекції. Так, зображення тетраедра
184 |
Розділ 2. Паралельність прямих і площин |
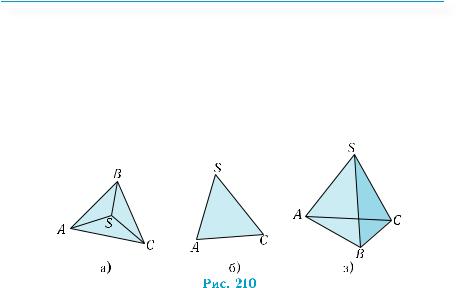
SABC на рис. 210, а), б) не можна вважати вдалими. У першому випадкувикористанопаралельнепроектуваннянаплощинуграні АВС, а у другому — напрям проектування визначається прямою АВ. В обох цих випадках втрачена об’ємність фігури. У загальному випадку використовують третє зображення (рис. 210, в). Воно є плоским чотирикутником ABCS, у якому проведені діагоналі АС і SB. Невидиме ребро АС зображено штриховою лінією.
Важливим засобом забезпечення наочності зображення є зображення елементів фігури (медіан, бісектрис, середніх ліній, діагоналей тощо), а також найпростіших перерізів.
Побудова зображень різних фігур є невід’ємною складовою розв’язання задач стереометрії.
Часто-густо при розв’язуванні задач необхідно виконати певні побудови на зображенні (провести медіану, вказати центр вписаного кола, побудувати переріз тощо). Ці побудови зазвичай виконуються за властивостями паралельного проектування.
Приклад 1. На довільному зображенні прямокутного рівнобедреного трикутника АВС побудувати зображення:
1) центра О описаного кола; 2) вписаного квадрата, дві сторони якого лежать на катетах три-
кутника, а одна з вершин — на гiпотенузi ВА.
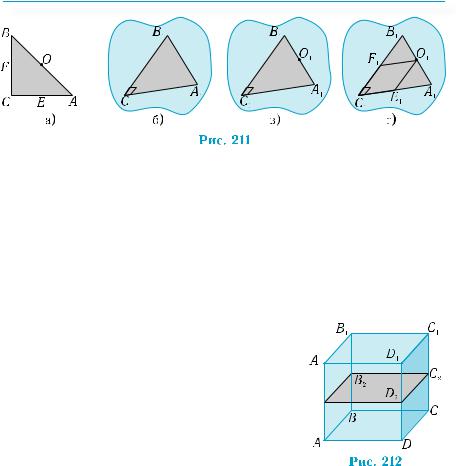
Нехай зображенням прямокутного рівнобедреного трикутника АВС (рис. 211, а) є трикутник A1B1С1 (рис 211, б).
1) Центр описаного навколо прямокутного трикутника кола є серединою гіпотенузи. Тому його зображення є серединою зображення гіпотенузи.
Побудова. Розділимо відрізок A1B1 навпіл, точка поділу О1 і є шуканою (рис. 211, в).
Зображення фігур у стереометрії |
185 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Якщо із середини О гіпотенузи АВ провести перпендикуляри докатетів(див.рис.211,а),тоотримаємоквадрат,якийзадовольняє умову завдання. Проведені перпендикуляри паралельні катетам. Саме цим скористуємось для побудови шуканого зображення.
Побудова. З точки О1 проводимо відрізки О1Е1 і O1F1, паралельні С1В1 і С1А1 відповідно (рис. 211, г). Чотирикутник С1Е1O1F1 є шуканим.
Приклад 2. На зображенні куба побудувати його переріз площиною, що проходить через середини трьох паралельних ребер.
На рис. 212 середини ребер АА1, ВВ1,
СС1, DD1 куба ABCDA1B1C1D1 позначено відповідно через А2, В2, С2, D2. Зображення
цих точок лежать на серединах зображень  відповідних відрізків (чому?). Нехай січна площина проходить через точки А2, В2, D2.
відповідних відрізків (чому?). Нехай січна площина проходить через точки А2, В2, D2.  Оскільки всі грані куба — квадрати, то відрізок А2В2, який проходить через середини протилежних сторін квадрата АА1В1В, дорівнює стороні квадрата АВ (або ж ребру куба) і паралельний цій стороні.
Оскільки всі грані куба — квадрати, то відрізок А2В2, який проходить через середини протилежних сторін квадрата АА1В1В, дорівнює стороні квадрата АВ (або ж ребру куба) і паралельний цій стороні.
Аналогічно D2C2 || DC і D2C2 = DC. Оскільки і АВ || DC, то, згідно з транзитивністю відношення паралельності, А2В2 || D2C2. Через паралельні прямі А2В2, D2C2 проходить єдина площина. У цій площині лежать точки А2, B2, D2, тому дана площина є шуканою січною. Січна площина перетинає грані куба по рівних відрізках А2В2, B2C2, C2D2 і D2A2. Отже, чотирикутник A2B2C2D2, що є шуканим перерізом, має форму ромба. Неважко помітити, що діагоналі B2D2 і А2С2 цього ромба рівні між собою. Тобто, чотирикутник A2B2C2D2 — квадрат. Ми не тільки побудували переріз, а й встановили його форму. ■

186 Розділ 2. Паралельність прямих і площин
Розглянемо обґрунтування наведених вище висновків стосовно зображення основних плоских фігур.
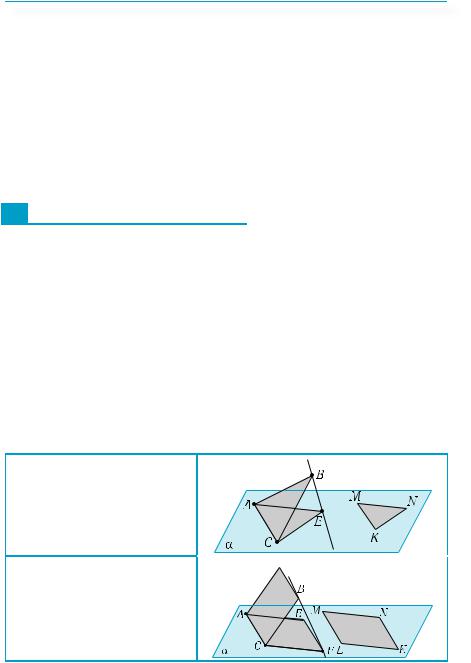
Теорема 1 (про зображення трикутника).
Будь-який трикутник може бути зображенням даного трикутника.
Нехай дано трикутник АВС. Візьмемо довільний трикутник KMN. Він може бути зображенням трикутника АВС, якщо існують площина проекцій і напрям проектування, притому такі, що паралельна проекція трикутника АВС подібна трикутнику KMN.
Виберемо площину проекцій α так, щоб вона перетинала площину трикутника АВС по прямій АС (рис. 213). Нам треба вибрати напрям проектування так, щоб проекцією трикутника АВС на площину α був трикутник, подібний трикутнику KMN. Для цього побудуємо у площині α трикутник САЕ, подібний трикутнику
KМN з коефіцієнтом подібності MKAC . Тоді пряма BE задає потріб-
ний напрям проектування. Оскільки трикутник САЕ є паралельною проекцією трикутника АВС, а трикутники САЕ і KMN — подібні, то трикутник KMN є зображенням трикутника АВС. ■
!Ця теорема відкриває широкі можливості для вибору зображень даного трикутника, хоча, звісно, не варто використовувати зображення із властивостями, яких не має оригінал. Наприклад, недоцільно зображати довільний трикутник у вигляді прямокутного.
Переходячи до зображень інших многокутників, зауважимо, що для них, як правило, теореми, аналогічні теоремі 1, не справджуються, хоча окремі їхні властивості зберігаються при зображенні. Передусім йтиметься про паралельність сторін (чому?). У зв’язку з цим наведемо ще одну важливу теорему.
Зображення фігур у стереометрії |
187 |
Теорема 2 (про зображення паралелограма).
Будь-який паралелограм може бути зображенням даного паралелограма.
Довести цю теорему можна, розбивши паралелограми діагоналями на трикутники і скориставшись теоремою 1 (див. рис. 206, а, б).
Ми вже зустрічались з ситуаціями, коли планіметричні факти мають аналоги у просторі. І такі випадки зустрічатимуться й далі. Найпростішій просторовій фігурі — тетраедру — відповідає на площині трикутник. За теоремою 1, будь-який трикутник може бути зображенням даного трикутника. З іншого боку, тетраедр проектується в чотирикутник, який після проведення в ньому діагоналей стає зображенням тетраедра. Виникає запитання: чи довільний чотирикутник може бути зображенням даного тетраедра? Ствердну відповідь на нього дає теорема німецьких математиків Польке К. (1810–1877) і Шварца Г. (1843–1921). Виходячи з неї, можна будувати зображення многогранників. Для цього треба вибрати чотири вершини, що не лежать в одній площині. Вони є вершинами якогось тетраедра. Потім задати довільним чином зображення цих точок. А вже тоді добудовувати зображення всієї фігури, користуючись властивостями проектування.
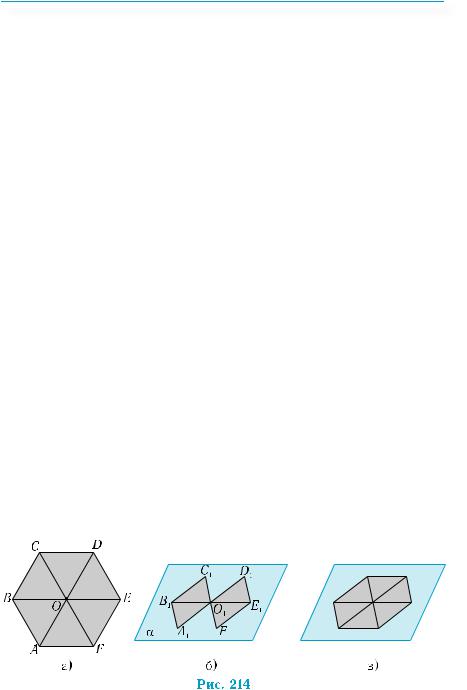
Приклад 3. Побудувати зображення правильного шестикутника.
Розглянемо правильний шестикутник ABCDEF (рис. 214, а). Він має властивості, які повинні зберігатись у його зображеннях. Сторони шестикутника попарно паралельні (АВ || ED, ВС || FЕ, CD || AF). Він має центр симетрії О, а відрізки, що сполучають точку О з вершинами шестикутника, рівні між собою і дорівнюють його стороні. Тепер неважко помітити, що досить побудувати зображення паралелограма (навіть ромба) АВСО, аби потім добудувати до нього зображення всього шестикутника.
188 |
Розділ 2. Паралельність прямих і площин |
Нехай паралелограм А1В1С1О1 є зображенням паралелограма АВСО (це може бути довільний паралелограм!). Продовживши А1О1 і С1О1 за точку О1 так, щоб О1D1= А1О1, О1F1 = С1О1, побудуємо паралелограм F1O1D1E1 (рис. 214, б). По суті, побудовано паралелограм, центрально-симетричний до паралелограма А1В1С1О1 відносно його вершини О1. Сполучивши точки А1 і F1, С1 і D1, дістанемо зображення правильного шестикутника (рис. 214, в). ■
Контрольні запитання
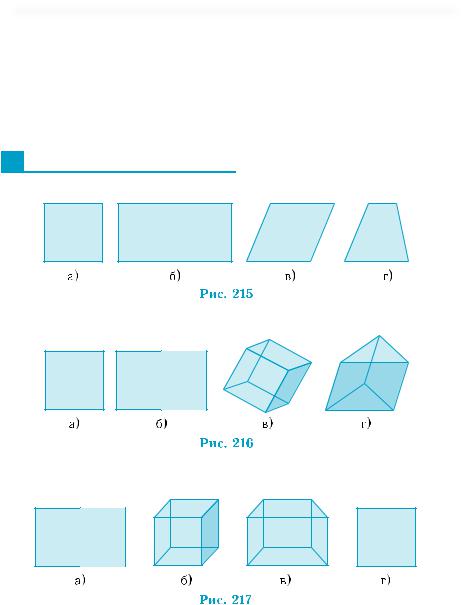
1.Котра з фігур на рис. 215, а)–г) не є зображенням квадрата?
2.Котра з фігур на рис. 216, а)–г) не є зображенням куба?
3.На котрому з рис. 217, а)–г) зображення куба не є правильним?
4.На котрому з рис. 218, а)–г) зображення тетраедра не є правильним?
5.Чи є паралельна проекція фігури її зображенням?

Зображення фігур у стереометрії |
189 |
6.Чи можна прямокутний трикутник вважати зображенням рівнобедреного трикутника?
7.Чи правильно, що зображенням середньої лінії трикутника є середня лінія його зображення?
8.Чи може паралелограм бути зображенням трапеції?
9.Чи може трикутник бути зображенням тетраедра?
10.Чи можна тетраедр зобразити так, щоб тільки одна його грань була невидимою?
11.Яка найменша кількість ребер куба може бути видимою при зображенні? А найбільша?
12.Якою фігурою є зображення: а) відрізка; б) трикутника; в) трапеції; г) паралелограма; ґ) n-кутника?
Графічні вправи
1.Встановіть, яким граням тетраедра ABCD, зображеного на рис. 219, належать точки P, K, M?
2.Які пари точок з точок X, Y, Z, T, вказаних на зображенні тетраедра на рис. 220, не лежать в одній грані?

190 |
Розділ 2. Паралельність прямих і площин |
3.Якою фігурою є переріз куба площиною, що проходить через точки M, N, P, вказані на рис. 221, а)–г)?
Задачі
174°. Дано зображення рівнобедреного трикутника у вигляді різностороннього трикутника. На цьому зображенні побудуйте зображення:
1) бісектриси кута при вершині;
2) перпендикуляра до основи, проведеного через середину бічної сторони; 3) ромба, дві суміжні сторони якого збігаються з бічними сто-
ронами трикутника.
175. На зображенні рівнобедреного прямокутного трикутника побудуйте зображення квадрата, що лежить у площині трикутника, якщо стороною квадрата є:
1°) катет даного трикутника; 2) гіпотенуза даного трикутника.
176. На довiльному зображеннi рiвностороннього трикутника АВС побудуйте зображення:
1°) точки перетину висот трикутника;
2°) «описаного» прямокутника, одна зі сторiн якого збігається з деякою стороною трикутника, а iнша мiстить протилежну вершину;
3) бiсектриси зовнiшнього кута трикутника.
177. Данозображеннятрикутникаідвохйоговисот.Побудуйтезображення центра кола, описаного навколо цього трикутника.
178. На зображенні прямокутного трикутника, один із гострих кутів якого дорівнює 60°, побудуйте зображення:
1) бісектриси цього кута;
2) висоти, що проведена до гіпотенузи;
3) центра вписаного кола.

Зображення фігур у стереометрії |
191 |
179°. Побудуйте зображення ромба і його висоти, проведеної з вершини кута, величина якого становить 120°.
180. Побудуйте зображення квадрата, маючи зображення точки перетину його діагоналей і двох:
1°) сусідніх вершин;
2*) протилежних вершин.
181. На довiльному зображеннi рiвнобiчної трапецiї, бiчна сторона якої дорiвнює меншiй основi, побудуйте зображення: 1°) осi симетрiї трапецiї;
2) вписаного прямокутника, двi вершини якого лежать на бiльшiй основi й одна зі сторiн збігається з меншою основою;
3) центра кола, дотичного до бiчних сторiн i меншої основи трапецiї.
182. Дано зображення рівнобічної трапеції, кути при основі якої дорівнюють 45°. Побудуйте зображення:
1) центра кола, описаного навколо трапеції; 2*) центра кола, дотичного до меншої основи і бічних сторін.
183. Дано зображення кола і одного з його діаметрів. Побудуйте зображення радіусів кола, перпендикулярних до цього діаметра.
184. Дано зображення куба АВСDА1В1С1D1.
1°) Побудуйте лiнiю перетину площин DА1С1 i В1D1D.
2) Знайдiть довжину вiдрiзка цiєї лiнiї, який міститься в кубi, якщо ребро куба дорівнює а.
3) Побудуйте переріз куба площиною, яка проходить через центри трьох попарно суміжних його граней.
185. Дано зображення тетраедра АВСD, точки К, М i Р — середини DC, AD i BD, вiдповiдно.
1°) Побудуйте лiнiю перетину площин АСР i ВМК.
2) Знайдiть довжину вiдрiзка цiєї лiнiї, який мiститься в тетраедрi, якщо довжини всiх його ребер дорiвнюють а.
3) Побудуйте переріз тетраедра площиною, яка проходить через точки перетину медіан трьох його граней.
186. Побудуйте переріз тетраедра SABC площиною, що проходить через:
1°) середини ребер SA, SC i BC;
192 |
Розділ 2. Паралельність прямих і площин |
2) точку M на AS (AM : AS = 1 : 2), точку N на SC (CN : NS = = 1 : 2) і точку P на BC (CP : PB = 1 : 2);
3) середини ребер AS, AB та центр грані SBC; 4*) центри граней ASB, ABC і BSC.
187. Побудуйте переріз куба АВСDА1В1С1D1 площиною, що проходить через:
1) ребро СD і центр грані АА1В1В;
2) діагональ А1D і центр грані ВСС1В1;
3*) середини ребер АD, СD і точку В;
4*) центри граней СDD1С1, СВВ1С1 і точку А.
Вправи для повторення
188.Дві паралельні прямі перетято третьою прямою. Один з восьми утворених кутів дорівнює 50°. Чому дорівнює кожен з решти кутів?
189.Маємо куб АВСDА1В1С1D1.
1) Вкажіть усі ребра, паралельні ребру АА1.
2) Доведіть, що ребро DС паралельне лінії перетину площин
АВС1 і А1В1D.
3) Чи існує в площині АВС1 пряма, паралельна прямій А1D1? 4) Нехай а — довільний відрізок в грані куба. Побудуйте відрізок, паралельний відрізку а, в несуміжній грані куба.
Підсумок
Головні твердження
Будь-який трикутник може |
|
бути зображенням |
даного |
трикутника. |
|
Будь-який паралелограм може бути зображенням даного паралелограма.
може бути зображенням даного паралелограма. 
