Добавил:

quantum researchgate.net Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский государственный экологический университет

Предмет:

Аналитическая геометрия

Файл:

978-966-10-1272-0_Математика. Підручник для 10 класу. загальноосвітніх навчальних закладів. Рівень стандарту.pdf

Скачиваний:

981

Добавлен:

24.03.2018

Размер:

8.73 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2617 18 19 20 21 22 23 24 25 26 > Следующая >>>

§16. Тригонометричні формули додавання та наслідки з них

У даному параграфі розглянемо велику групу формул, пов’язаних з тим, що поворот на кут α +β можна реалізувати в результаті двох послідовних поворотів — на кут α і на кут β, та їхні застосування.

		1. Формули додавання
		Формулизведеннядозволяютьвважати,щокутиα і β
		Формулизведеннядозволяютьвважати,щокутиα і β
		належать проміжку [0; π]. Розглянемо на тригономе-
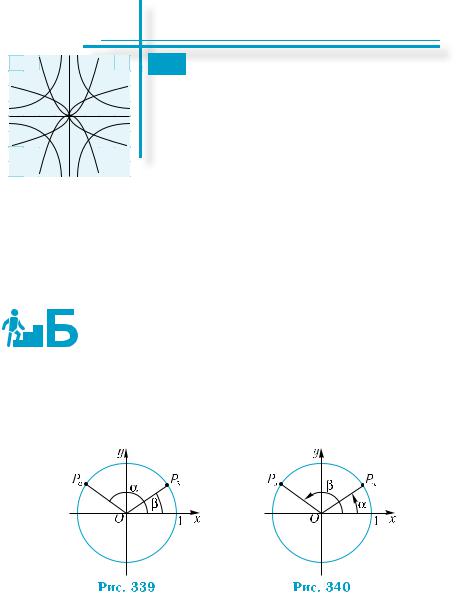
		тричному колі точки Рα і Рβ, маючи на увазі, що векто-
		тричному колі точки Рα і Рβ, маючи на увазі, що векто-
ри OPα	і OPβ утворюють кути α і β з віссю абсцис. Кут між вектора-
ми OPα	і OPβ може дорівнювати α −β, якщо α ≥ β (рис. 339),

β − α, якщо β > α (рис. 340). У будь-якому з цих випадків косинус цього кута дорівнює cos(α −β).

Точки Рα	і Рβ мають		відповідно			координати		(cos		α; sin α)
і (cos β; sin β). Такі самі координати мають і вектори OPα										і OPβ . За
означеннямскалярногодобутку, OPα						OPβ =			cos(α −β) =
							OPα	OPβ
= cos(α −β),	оскільки				=1.

		OPα	=	OPβ

Тригонометричні формули додавання та наслідки з них

299

Оскільки скалярний добуток векторів a = (x1 ; y1 ) і b = (x2 ; y2 ) виражається через їхні координати за формулою: ab = x1x2 + y1 y2 , то маємо:

OPα OPβ = cosα cosβ + sinα sinβ.

Порівнявши одержані результати, матимемо: cos(α −β) = cosαcosβ + sin αsinβ.

Косинус різниці двох кутів дорівнює сумі добутків косинусів та синусів цих кутів.

Як наслідок, отримуємо формулу косинуса суми кутів:

cos(α +β) = cos(α −(−β))= cosαcos(−β)+ sin αsin (−β).

З урахуванням парності косинуса і непарності синуса, одержимо:

cos(α +β) = cosαcosβ −sin αsinβ.

Косинус суми двох кутів дорівнює різниці добутків косинусів та синусів цих кутів.

Виведемо тепер формули синуса суми двох кутів. Скориставшись формулами зведення і косинуса різниці двох кутів, матимемо:

π			π				=
sin (α +β) = cos	2	−(α +β)	= cos	2	− α	−β	=
	2			2

	π			π
= cos		2	− α cosβ + sin		2	− α sinβ = sin αcosβ + cosαsinβ.
Отже,

sin (α +β) = sin αcosβ + cosαsinβ.

Синус суми двох кутів дорівнює добутку синуса першого кута на косинус другого плюс добуток косинуса першого кута на синус другого.

Для синуса різниці маємо:

sin (α −β) = sin (α + (−β))= sin αcos(−β)+ cosαsin (−β) = = sin αcosβ − cosαsinβ.

300	Розділ 3. Тригонометричні Функції

Таким чином,

sin (α −β) = sin αcosβ − cosαsinβ.

Синус різниці двох кутів дорівнює добутку синуса першого кута на косинус другого мінус добуток косинуса першого кута на синус другого.

Ïðèê ëàä 1. Не користуючись обчислювальними засобами,

знайти sin 15°.

 Представимо 15° у вигляді різниці 45° – 30°. Тоді, користуючись формулоюсинусарізницідвохкутів,знайдемо:sin15°=sin(45°–30°)=

=sin45°cos30°–cos45°sin30°=					2	3	−	2	1 =	2	( 3 −1).
=sin45°cos30°–cos45°sin30°=					2	2	−	2	1 =	4	( 3 −1).
	2				2	2		2	2	4
Відповідь.	2	( 3 −1).
Відповідь.	4	( 3 −1).									π
	4
Ïðèê ëàä 2 . Обчислити cos (α – β), якщо
Ïðèê ëàä 2 . Обчислити cos (α – β), якщо									cosα = −0,8, 2 < α < π,
sinβ = −12 , π < β <			3π						cosα = −0,8, 2 < α < π,
			3π	.
		2		.
13		2
 З формули косинуса різниці двох кутів випливає, що для
розв’язання задачі необхідно знайти sin α								і cos β. З основної тригоно-

метричноїтотожностіможназнайтиsin2α:sin2α=1–cos2α=1 – 0,64 =

= 0,36. Оскільки	π	< α < π, то sin α > 0, тому sinα =								0,36 = 0,6.
	2
Аналогічно обчислимо cos β. З основної тригонометричної тотож-
ності маємо: cos2 β =1 −sin2 β =1 −144 =								25	. Оскільки	π < β <	3π	,
ності маємо: cos2 β =1 −sin2 β =1 −144 =							169		. Оскільки	π < β <		,
				169			169			2
то cos β < 0 і cosβ = −			25	= −	5	. Тепер можна обчислити cos (α – β),
то cos β < 0 і cosβ = −		169		= −		. Тепер можна обчислити cos (α – β),
		169		13

за формулою косинуса різниці двох кутів: cos (α – β) = cos α cos β +

				5			12		16	.
+ sin αsinβ = −0,	8	−			+	−		0,6 = −
+ sin αsinβ = −0,	8	−	13		+	−	13	0,6 = −	65
			13				13		65
Відповідь. −	16 .
	65

Тригонометричні формули додавання та наслідки з них

301

Використовуючи одержані формули синуса і коси-
нуса суми двох аргументів, можна вивести формули
додавання для тангенса:
tg(α +β) = tgα + tgβ , tg(α −β) =	tgα − tgβ .
1 − tgαtgβ	1 + tgαtgβ

 Справді,

tg (α +β) = sin ((α +β)) = sin αcosβ + cosαsinβ. cos α +β cosαcosβ −sin αsinβ

Припускаючи, що cosα ≠ 0, cosβ ≠ 0 , і поділивши на cosα cosβ чисельник і знаменник останнього дробу, матимемо:

sin αcosβ

+ cosαsinβ

sin α + sinβ

tgα + tgβ

cosαcosβ

cosα

cosβ

tg (α +β) = cosαcosβ

sin αsinβ

1 − tgαtgβ

−

sin α

sinβ

cosαcosβ

cosα

cosβ

Отже, справджується твердження:

тангенс суми двох аргументів дорівнює сумі тангенсів доданків, поділеній на різницю між одиницею і добутком цих тангенсів.

Замінюючи β на (–β) і використовуючи непарність тангенса, одержимо формулу для тангенса різниці.

Тангенс різниці двох аргументів дорівнює різниці тангенсів зменшуваного і від’ємника, поділеній на суму одиниці і добутку цих тангенсів.

Аналогічно можуть бути виведені формули котангенса суми і різниці двох аргументів, але вони вживаються дуже рідко. За необхідністю їх можна вивести самостійно.

Ïðèê ëàä 3 . Обчислити tg 105°.

 Представимо 105° у вигляді суми 45° + 60°. Тоді, користуючись

формулою тангенса суми двох кутів, знайдемо: tg 105° = tg (45° + 60°) =

=	tg45°+ tg60°		1 +	3	(1 +	3 )(1 +	3 )		4 + 2 3	= −2 − 3.
		=	1 −	3	= (1 −	3 )(1 +	3 )	=	−2
	1 − tg45° tg60°

Відповідь. −2 − 3.

302 Розділ 3. Тригонометричні Функції

	Контрольні запитання
1°.	Чому дорівнює значення виразу sin 22°cos23°+ cos22°sin 23°?
2.	Чому дорівнює значення виразу	tg86°− tg26°	?
2.	Чому дорівнює значення виразу	1 + tg86° tg26°	?
		1 + tg86° tg26°

3.Як за допомогою формули для тангенса суми двох кутів обчислити tg75°?

Чи можна стверджувати що:

5.	Чи можна з формули для косинуса суми двох кутів вивести
	формулу для косинуса різниці двох кутів?
6.	Чи можна обчислити:								4
	1)	cos	π		+ α		, якщо відомо, що sin α =			;
									5
			4					1
	2)		π			,	якщо відомо, що tgα =		;
		tg	4	+ α				2

3)	sin(	α −β),			якщо відомо, що sinα = −					15 , cosβ =	4 ;
	tg (α −β), якщо відомо, що tgα = 6 ,									17	5
4)	tg (α −β), якщо відомо, що tgα = 6 ,									tgβ = 7 ?
									5	10
7*. За яких умов не має змісту формула тангенса різниці двох
кутів?		π		π		π		π
а)		π	+	π	= sin	π	+ sin	π	;
а)	sin	3	+		= sin	3	+ sin	4	;
		3		4		3		4
б)sin63°cos12°+cos63°sin12°=sin32°cos43°+sin43°cos32°?

8*. Чи можна за допомогою формул додавання обчислити зна-

π			?
чення tg α, якщо відоме значення tg	4	+ α

2.Тригонометричні функції подвійного

іполовинного аргументів

Як наслідок формул додавання при α = β одержи- мо формули подвійного кута:

sin 2α = sin(α + α) = sin αcosα + cosαsin α = 2sin αcosα;

cos2α = cos(α + α) = cosαcosα −sin αsin α = cos2 α −sin2 α.

Отже,

sin 2α = 2sin αcosα; cos2α = cos2 α −sin2 α.

Тригонометричні формули додавання та наслідки з них

303

Ïðèê ëàä 4. Знайти значення cos 2α, якщо sin α = –0,8.  За формулою косинуса подвійного кута маємо:

cos2α = cos2 α −sin2 α =1 −sin2 α −sin2 α =1 −2sin2 α =1 −2 (−0,8)2 =

=–0,28.

Відповідь. –0,28.

Ïðèê ëàä 5 . Спростити вираз:	2cos2 α −1	.

	sin α cosα
 Застосовуючи послідовно основну тригонометричну тотож-

ність, формулу синуса подвійного кута, формулу косинуса подвій-
ного кута і означення котангенса, дістанемо:
	2cos2 α −1	= 2cos2 α − cos2 α −sin2 α	=	cos2α	= 2ctg 2α .
	sin α cosα			1
		1
		2 sin 2α		2 sin 2α
Відповідь. 2ctg 2α .

Зформул подвійного кута можна вивести формули для синуса

ікосинуса половинного кута. Фактично ми це почали реалізовувати при розв’язанні прикладів 4 і 5. Справді,

cos2α = cos2 α −sin2 α = cos2 α − (1 − cos2 α) = 2cos2 α −1,

або

cos2α = cos2 α −sin2 α =1 −sin2 α −sin2 α =1 −2sin2 α.

Ці рівності часто записують у такому вигляді:
	1 + cos2α = 2cos2 α,			1 − cos2α = 2sin2 α.
Оскільки
cosα = cos2 α		= 2cos2 α −1,		cosα = cos2 α =1 −2sin2 α ,
2			2		2		2
то
	cos2 α		= 1 + cosα	, sin2 α	= 1 − cosα.
		2	2	2	2
Ці формули називаються формулами половинного аргу-
менту, чи формулами зниження степеня.
	Як наслідок формули додавання для тангенса при
	Як наслідок формули додавання для тангенса при
	α = β	одержимо формулу тангенса подвійного кута:
		tg2α = tg (α + α) =			tgα + tgα	=	2tg α	.
		tg2α = tg (α + α) =				=		.
					1 − tgαtgα		1 − tg2α

304	Розділ 3. Тригонометричні Функції

Отже, tg 2α = 12−tgtgα2α.

Ïðèê ëàä 6 . Знайти значення tg 2α, якщо tg α = –0,5.

 За формулою тангенса подвійного кута, маємо:

tg2α =

2tgα

2 (−0,5)

= −

4 .

1 − tg2α

1 −(−0,5)2

Відповідь.

−

4 .

Формули половинного аргументу можна записати у вигляді:

cos α

1 + cosα

sin α

1 − cosα

!Звернемоувагунате,щознаючитількиcosα ,неможливо без додаткових умов однозначно знайти cos α2 або sin α2 .

Зостанніх двох формул випливає формула для тангенса половинного кута:

tg α

1 − cosα.

1 + cosα

3 , π ≤ α ≤ 2π.

Ïðèê ëàä 7.

Обчислити cos α , якщо cosα = −

≤ π, то cosα

1 + cosα

1 −

Оскільки

≤

< 0, cos

= −

= −212 .

Відповідь. −212 .

Ïðèê ëàä 8 . Не користуючись обчислювальними засобами,

знайти sin 15°.

 Один спосіб розв’язання цього завдання, який ґрунтувався на застосуванні формули косинуса різниці двох кутів, було наведено у п. 1 (приклад 1). Тут розглянемо інший спосіб.

Скориставшись формулою синуса половинного аргументу, враховуючи, що sin 15° > 0, одержимо:

Тригонометричні формули додавання та наслідки з них

305

sin15° = sin 30°				1	− cos30°		1 −		3		1
			=	1	− cos30°	=	1 −		2	=	1	2 − 3 =
			=		2	=		2		=	2	2 − 3 =
		2			2			2			2
	1	1		2			2			2
=	2 2 (4 −2 3)		=		1 −2 3	+( 3)			=		( 3 −1).
=	2 2 (4 −2 3)		=	4	1 −2 3	+( 3)			=	4	( 3 −1).
	Відповідь.		2	(	3 −1).
	Відповідь.		4	(	3 −1).
			4

Важливу роль у тригонометрії та її застосуваннях відіграє тангенс половинного кута. Через нього можна виразити всі інші тригонометричні функції:

α cos α

2sin

α cos

2tg

sinα = 2sin

2 α

cos

+ sin

+ tg

2 α

(чисельник і знаменник поділили на cos2

2 ).

Аналогічно,

cos2

cos2 α

−sin2 α

1 − tg2 α

cosα =

;

cos

+ sin

2 α

+ tg

2 α

sin α

2tg

tgα =

cosα

− tg

2 α

Одержані формули називаються формулами універсальної

підстановки. Вони дозволяють звести доведення будь-якої тригонометричної тотожності чи розв’язання рівняння, в обох частинах яких стоять раціональні вирази відносно sinα і cosα, до доведення алгебраїчної тотожності чи розв’язання алгебраїчного рівняння з однією змінною. Для цього достатньо виразити sinα

і cosα через tg α2 і позначити tg α2 через t.

20 Математика, 10 кл.

306	Розділ 3. Тригонометричні Функції

 Контрольні запитання

1.Чому дорівнює: а°) sin 15° cos15°; б°) cos222,5° – sin222,5°;

3°.

8*.

в)	2tg75°	?
	1− tg2 75°

Чому дорівнює: а°) sin 50°, якщо sin 25° = а; б) tg 70°, якщо tg 35° = a?

Чи існує такий кут α, що sinαcosα = 0,65?

Чи потрібно знати, в якій чверті знаходиться точка Рα, щоб за значенням cos α або sin α обчислити: а) cos 2α; б) sin 2α?

У якій чверті тригонометричного кола знаходиться точка Pt,

якщо sin t > 0, sin 2t < 0?

Якою є множина значень функції y = sin2 x – cos2 x?

Чи завжди можна стверджувати, що sin α		=	1 − cosα ?
Чи можна стверджувати, що знак tg x	2		2
Чи можна стверджувати, що знак tg x	збігається зі знаком sin x
2
для всіх допустимих значень х?

3. Перетворення суми тригонометричних функцій на добуток

При розв’язуванні тригонометричних рівнянь або нерівностей корисно вміти подавати суму і різницю синусів або косинусів у вигляді добутку тригонометричних функцій. Такі формули широко застосовуються у різних перетвореннях тригонометричних виразів.

Формули, на яких ґрунтуються перетворення суми тригономе-

тричних функцій на добуток, можна одержати з формул додавання.

Нехай необхідно перетворити суму sin α

+ sin β на добуток. За-

пишемо α і β у вигляді α =

α +β

α −β

β =

α +β

−

α −β

. Тоді

α +β

α −β

α +β

−

α −β

sin α + sinβ = sin

+ sin

=sin α2+βcos α2−β + cos α2+βsin α2−β + sin α2+βcos α2−β −

−cos α2+βsin α2−β = 2sin α2+βcos α2−β.

Тригонометричні формули додавання та наслідки з них	307
Таким чином,
sin α + sinβ = 2sin α +βcos	α −β.
2	2
Одержали формулу суми синусів двох кутів.

Сума синусів двох кутів дорівнює подвоєному добутку синуса півсуми цих кутів на косинус їхньої піврізниці.

Аналогічно виводяться формули	різниці синусів, суми
і різниці косинусів. Формула різниці синусів:
sin α −sinβ = 2sin α −βcos α +β.
2	2

Різниця синусів двох кутів дорівнює подвоєному добутку синуса піврізниці цих кутів на косинус їхньої півсуми.

Формула суми косинусів:

cosα + cosβ = 2cos α2+βcos α2−β.

Сума косинусів двох кутів дорівнює подвоєному добутку косинуса півсуми цих кутів на косинус їхньої піврізниці.

Формула різниці косинусів:

cosα − cosβ = −2sin α2+βsin α2−β.

Різниця косинусів двох кутів дорівнює взятому із знаком “мінус” подвоєному добутку синуса півсуми цих кутів на синус їхньої піврізниці.

Рекомендуємо вивести формули різниці синусів, суми і різниці
косинусів самостійно.
Ïðèê ëàä			9. Обчислити без обчислювальних засобів:
1) cos 75°			cos 15°; 2) cos 5π + cos				π	.

			12			12
 1) Скористаємось формулою різниці косинусів двох аргумен-
тів:cos75°− cos15° = −2sin 75°+15°						sin 75°−15° = −2sin 45°sin30° =
			2			2
= −2	2	1	= −	2	.
	2	2
			2

20*

308	Розділ 3. Тригонометричні Функції

5π π

2)cos 125π + cos12π = 2cos 12 2−12 cos 12 2+12 = 2cos 6π cos 4π =

=2 23 22 = 26 .

Відповідь. 1) −

; 2)

Формули

перетворення

суми

тригонометричних

функцій у добуток дозволяють розв’язувати різно-

манітні задачі.

Ïðèê ëàä 10 . Довести тотожність: cosα −sin α =

2 cos

α +

 Скориставшись формулами зведення, замінимо cosα

на

, застосуємо формулу різниці косинусів двох кутів і не-

sin

− α

парність синуса:

α +

− α

α −

− α

= −2sin

sin

cosα −sin α = cosα − cos

− α

= −2sin

sin

α −

= 2

sin

− α =

2 cos

−

− α

= 2 cos

+ α .

Останнє перетворення здійснено за допомогою формули зве-

дення: sin α = cos

− α

З формул додавання можна одержати формули для суми і різ-

ниці тангенсів двох кутів:

tg α + tg β = sin(α +β) ;

tg α − tg β = sin(α −β) .

cosαcosβ

Сума тангенсів двох кутів дорівнює відношенню синуса суми цих кутів до добутку косинусів тих самих кутів.

Тригонометричні формули додавання та наслідки з них

309

Різниця тангенсів двох кутів дорівнює відношенню синуса різниці цих кутів до добутку косинусів тих самих кутів.

Доведемо, наприклад, першу з наведених формул.

 tg α + tg β = sin α	+ sinβ	= sin αcosβ + sinβcosα	= sin(α +β) .
cosα	cosβ	cosαcosβ	cosαcosβ

Друга формула доводиться аналогічно. Рекомендуємо зробити це самостійно.

Формули перетворення різниці однойменних функцій двох ар-

гументів у добуток дозволяють одержати умови, за яких функції двох аргументів дорівнюють одна одній.

Ïðèê ëàä 11. Знайти умову, за якої синуси двох кутів дорівню-
ють один одному.
Нехайsinx=siny.Тодіsinx–siny=0,або 2sin	x − y	cos	x + y		= 0.

2				2
Остання рівність справджується тоді, і тільки тоді, коли принаймні
один із співмножників дорівнює нулю. Якщо sin		x − y		= 0,	то

2

x 2− y = πn (див. § 15), або x – y = 2πп, або x = y + 2πп, п Ζ. Якщо ж cosx +2 y = 0,то x +2 y = 2π + πn, x + y = π + 2πn, x = −y + π(2n +1),n Z.

Відтак, якщо синуси двох кутів х і у дорівнюють один одному, то справджується одне із співвідношень x = y + 2πп, або

x= −y + π(2n +1),n Z.

Зіншого боку, якщо справджується одне із зазначених співвід-

ношеньx =y +2πп,або x = −y + π(2n +1),n Z ,тоsinx =sin(y +2πn)=

=sin y, або sin x = sin (–y + 2πn + π) = sin(π – y) = sin y.

Співвідношення x = y + 2πп, x = −y + π(2n +1),n Z , можна за-

писати за допомогою однієї рівності: x = (–1)ky + πk, k Ζ. Справді, якщо k = 2n, то маємо перше співвідношення, при k = 2n + 1 — друге.

Відповідь. x = (–1)ky + πk, k Ζ.

Аналогічно можна одержати умову рівності двох косинусів, двох тангенсів. Радимо зробити це самостійно.

310 Розділ 3. Тригонометричні Функції

1°.	Чому дорівнює значення виразу:
	а) sin 124° + sin 236°;	б) cos 137° + cos 43°?
2°.	Як можна вивести формулу суми косинусів, використовуючи
	формулу суми синусів і формули зведення?
 Контрольні запитання
3.	Як порівняти cos 3 і cos 3,2, користуючись формулою різниці
	косинусів двох аргументів?
4.	Що більше: tg 3 чи tg 4,8?
5.	Як перетворити суму синуса і косинуса двох аргументів на до-
	буток?

Задачі

318°. Скориставшись формулами додавання, доведіть такі фор-

мули зведення:

2) cos (270° +α) = sinα ;

1) sin (180° – α ) = sinα ;

3) cos(π − α) = −cosα;

3π

4) sin

− α = −cosα.

319.

Скориставшись формулами додавання, обчисліть:

1) cos 75°;

2) cos 105°; 3) sin 15°;

4) sin 75°;

5) cos 165°.

320.

Обчисліть:

– sin 8°cos 68°;

1°) sin 68°cos 8°

2°) cos 10°cos 35° – sin 10°sin 35°;

3) sin 54°sin 24°

– sin 66°cos 126°;

4) cos 21°cos 24°

– cos 69°cos 66°.

321°. Знайдіть:

sin(α +β),

sin(α −β),

якщо

sin α = −

;

cosβ =

;

3π

, 0 < β < π;

π < α <

cos(α +β), cos(α −β), якшо cosα = −1 ;

cosβ =

1 ;

π < α < π,

32π < β < 2π;

3)tg(α +β) , tg(α −β) , якщо tg α = 35 ; tg β = 52 .

4)tg (45° − α) , якщо sin α = −1213 , 180° < α < 270° .

Тригонометричні формули додавання та наслідки з них

311

322°. Спростіть вираз:

3π

α −

;

cos

+ sin

sin

;

sin α +

−sin

sin(α +β) + sin(α −β) ;

cos(α +β) − cos(α −β) .

sin(α +β) −sin(α −β)

cos(α +β) + cos(α −β)

sin15° + tg 30°cos15°;

sin α + ctg 2αcosα .

323.Доведіть тотожність:

1°) sin (α +β)+ sin (α −β) = 2sin α cosβ; 2°) sin (α +β)−sin (α −β) = 2sinβ cosα;

3)sin (α +β) sin (α −β) = sin2 α −sin2 β;

4)cos(α +β) cos(α −β) = cos2 α −sin2 β .

324*. Доведіть, що:				2 , tgβ = 3 ,0 < α <
1)	α +β =	π,	якщо tgα =	2 , tgβ = 3 ,0 < α <		π,0 < β < π;
		4		5	7	2		2
2)	α +β =	π,	якщо ctgα = 1 ,ctgβ = −2,0 < α <				π, −	π < β < 0.
		4		3			2	2
325. Доведіть нерівність:					2) cos 15° – cos45° < 0,3.
1) cos 75°		+ cos 15° > 1;			2) cos 15° – cos45° < 0,3.
Доведіть:			і β — кути		гострокутного		трикутника, то
1)	якщо	α	і β — кути		гострокутного		трикутника, то
tgα tgβ >1;
2)	якщо α і β — гострі кути тупокутного трикутника, то

tgα tgβ <1.

327.Синуси двох гострих кутів трикутника дорівнюють, відпо-

відно, 2029 і 35 . Знайдіть косинус зовнішнього кута трикутника, що не є суміжним з двома даними кутами.

Тангенси трьох гострих кутів дорівнюють, відповідно,

35 , 43 ,198 . Доведіть, що сума перших двох кутів на 45° пере-

вищує третій кут.

329. Знайдіть найменший додатний період і побудуйте графік функції:

1) y = sin x sin 2x – cos x cos 2x; 2) y = sin 3x cos x – cos 3x sin x;

312	Розділ 3. Тригонометричні Функції

sin 2x

+ cos

y = 2 sin

cos2x .

330.

Знайдіть:

1°) sin 2α; cos2α , якщо sinα =

< α < π ;

2°) sin50°, якщо sin 25° = a;

2π

3°)

cosπ,

якщо cos

= a;

4) tg

, якщо tg π

= a.

331.

Знайдіть: sin

α; cos α

; tg

α ,

якщо:

π;

2) sinα = 0,6; π

1) cosα = 0,6; 0 < α <

< α < π .

332.

Спростіть вираз:

2°) cos2 2α −sin2 2α ;

1°) sin 10° cos 10°;

3°) cos2 α −4 sin2 α cos2 α ;

tg (45 − α)

;

1 − tg2 (45 − α)

5°) 2sin αcosα(cos2 α −sin2 α); 6°) cos4 (45

− α) −sin4 (45 − α);

sin

−sin

8) cos

α −

+ α

− α ;

− cos

α +

;

1 − cos2γ

;

10)

1 −sin 2γ

1 + cos2γ

1 + sin 2γ

333.

Спростіть вираз:

2sin

tgα tgβ + (tgα + tgβ) ctg(α +β) ;

− α + sin 2α ;

1 −sin 2α

;

−

;

1 + sin 2α

1 − tgα

1 + tgα

5)		1	−		1	;
	1 + ctgα			1 − ctgα

7) 1 −8sin2 β cos2 β;
9)		tg2α tgα			;	10)
		tg2α − tgα

12*) 2sin 2α + 2 ;

6) sin α(1 + 2cos2α) ;
8) 0,125 – cos2x + cos4x;
tgα	;	11)	1 −sin 2α	;
tg2α − tgα	;	11)	cosα −sin α	;
tg2α − tgα			cosα −sin α
13)	2(1 + cos2α), π < α < π ;
			2

Тригонометричні формули додавання та наслідки з них

313

14*)

1 −sin α − 1 + sin α,0 < α <

π .

334. Доведіть, що:

2sin2 α

+ cosα =1;

2) 2cos2 α − cos2α =1;

cos2α

= ctg

− α ;

= tg

− α

;

1 −sin 2α

1 + sin 2α

5) sin 2α – tg α = cos 2αtgα; 6) (ctg α – tg

α) sin 2α = 2cos 2α;

1 + sin α = 2cos

−

8) 1 −sin α = 2sin

−

;

335*. Обчисліть:

2π

cos π

cos

;

2) cos20°cos40°cos60°cos80° ;

cos π

cos 4π

cos

5π ;

−

sin

cos

336.

Дано функцію:

= sin

;

− x

+ (sin x − cos x)

y = 2cos2x + sin2 x .

Знайдіть її найменше і найбільше значення, найменший

додатний період, побудуйте її графік.

337*. 1)

Косинус кута при основі рівнобедреного трикутника до-

рівнює 0,8. Знайдіть синус і косинус кута при вершині цього

трикутника.

Косинус кута при вершині рівнобедреного трикутника до-

рівнює

. Знайдіть синус і косинус кута при основі цього

трикутника.

Знайдіть найменше значення площі прямокутного трикут-

ника, в якого висота, що проведена до гіпотенузи, дорівнює h.

338.

Дано функцію:

2*) y = 2sin22x + cos2 2x;

1) y

= sin xcos x;

3*) y = sin 2x(ctg x – 2ctg 2x).

Знайдіть найбільше і найменше значення функції та її найменший додатний період. Побудуйте її графік.

314 Розділ 3. Тригонометричні Функції

339°. Обчисліть, не користуючись обчислювальними засобами:

sin

7π

+ sin

;

2) sin

11π

−sin 5π;

3) cos

11π

+ cos 5π;

cos

7π

− cos

;

5) cos 75° cos 105°;

6) sin 75° sin 15°.

340. Спростіть вираз:

1°)

sin α + sin3α

;

2°)

2(cosα + cos3α)

;

cosα + cos3α

2sin 2α + sin 4α

3*) 1 + sin α + cosα;

4) cos2 α −sin2 2α.

341. Доведіть, що:

cos

α −sin

;

α + sin 2α = 2 cos 2α −

2)sin 2α + sin 4α −sin3α = tg 3α; cos2α + cos4α − cos3α

3)(sin α + sinβ)2 +(cosα + cosβ)2 = 4 cos2 α2−β;

4)(sin 2α + sin 4α)2 +(cos2α + cos4α)2 = 4 cos2 α;

2α +

1 + ctg2α

sin

= 2tgα;

− tg

−

1 − ctg2α

2α −

sin

342. Подайте даний вираз у вигляді добутку або частки:

2 + 2cosα;

3 −2cosα;

3) 3 − tgα;

4) 1 + tgα.

343.

Зменшіть степінь тригонометричної функції у виразі:

1°) 2cos2x;

2) 2cos2x cos 2x; 3°) 2sin2 2x;

4°) cos2 4x.

344*. Знайдіть умову, за якої дорівнюють один одному:

і β.

1) косинуси двох кутів α і β;

2) тангенси двох кутів α

345.

Доведіть, що:

cos

2π

+ cos

4π

+ cos

6π

= −1 ;

2) cos π + cos

3π

= 1 ;

3)1 + sin x + 1 −sin x = 2cosx2 , якщо 0 ≤ x ≤ 2π;

4)1 + sin x − 1 −sin x = 2sin 2x , якщо 0 ≤ x ≤ 2π;

5) ctgα + ctgβ = sin(α +β)	;	6) ctgα − ctgβ = sin(β − α) .
sin αsinβ		sin αsinβ

Тригонометричні формули додавання та наслідки з них

315

346*.Доведіть тотожність, що коли α, β, γ — кути трикутника, то:

1)	sin α + sinβ + sin γ = 4 cos				α cos β cos			γ		;

2)					2	2	2
	tgα tgβ + tgβ tgγ + tgγ tgα =1					;
3)	tgα + tgβ + tgγ = tgα tgβ tgγ ;
4)	ctg α	+ ctg β + ctg	γ	= ctg α	ctg	β ctg	γ		.
			2				2
	2	2		2		2
347*. Тангенси двох кутів трикутника дорівнюють, відповідно, 1,5
і 5. Знайдіть третій кут трикутника.
348*. Дано функцію:					2) y = sin x – cos x.
1) y = sin x + cos x;

Знайдіть найбільше і найменше значення функції та її найменший додатний період. Побудуйте її графік.

Вправи для повторення

	π			π
	sin	3	− α	+ sin	4	+ α
349. Знайдіть значення виразу		3			4		, якщо α
349. Знайдіть значення виразу	π			π			, якщо α
	π			π
	cos	3	− α	− cos	4	+ α
		3			4

	набуває таких значень: 0,π			,−π,−	3π		.

350.			2			2
	Знайдіть основний період функції:
	1) y = 1 tgx + 2;	2)	y = −3sin5x;				3) y = 3cos x .
351.	2					4
	Знайдіть множину значень функції:
	1) y = 0,1tg 10x;			2) y		= 10sin 0,1x.
352.	Розв’яжіть нерівність:			2) xtg 4 > ctg 5.
	1) xtg 3 < ctg 6;

316	Розділ 3. Тригонометричні Функції

Назва формули

Формули

додавання

Формули

подвійного

аргументу

Формули зниження степеня

Формули

половинного

аргументу

Формули

універсальної

підстановки

Формули

перетворення

суми тригонометричних функцій

у добуток

Підсумок

Формули

cos (α – β) = cosα cosβ + sinα sinβ.

cos (α+ β) = cosα cosβ

– sinα sinβ.

sin (α + β)

= sin

α cos

+ cos

α sin

β.

sin (α

– β)

= sin

α cos

– cos

α sin

β.

tg (α +β) =

tg α + tg β

; tg (α −β) =

tg α − tg β

1 − tg αtg β

1 + tg αtg β

sin 2α = 2sin αcosα; cos2α = cos2 α −sin2 α;

tg 2α =

2tg α

1 − tg2α

cos

2 α

1 + cosα

;

sin

2 α

1 − cosα

cos α

1 + cosα

;

sin

1 − cosα.

tg α

1 − cosα .

1 + cosα

2tg α

1 − tg2 α

sinα =

;

cosα =

1 + tg2 α

2tg

tgα =

1 − tg2 α

sin α + sinβ = 2sin α +βcos α −β.

sin α −sinβ = 2sin α −βcos

α +β.

cosα + cosβ = 2cos

α +β

cos

α −β

cosα − cosβ = −2sin

α +β

sin

α −β

tg α + tg β = sin(α +β)

;

tg α − tg β = sin(α −β) .

cosαcosβ

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2617 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете Аналитическая геометрия