
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач

§21. ортогональне проектування
Ðозглядається проектування за напрямом, перпендикулярним до площини проекції, та його застосування.
Введення понять перпендикулярності прямої і пло 
 щини, перпендикулярності площин дає змогу по
щини, перпендикулярності площин дає змогу по  вернутись до питань про зображення просторових
вернутись до питань про зображення просторових
геометричних фігур. Як вже відзначалось, якість зображень у стереометрії, тобто можливість за ними отримати найбільш повне уявлення про фігуру, залежить від вибору напряму паралельного проектування. Серед усіх можливих напрямів проектування ви діляється напрям, перпендикулярний до площини проекцій. По перше, такий напрям лише один. Подруге, він найприродніший для сприйняття людиною (рис. 438 – 440).
Такимчином,однимізважливихугеометріїтаїїзастосуваннях окремим випадком паралельного проектування є ортогональне проектування, тобто проектування вздовж прямої, перпендику лярної до площини проекцій.
Ортогональний — від грецьких ορϑος (orthos) — прямий, вертикальний і γωνιa (gonia) — кут — буквально: прямокутний. Те саме, що й «перпендикулярний».
Ортогональне проектування |
407 |
Паралельна проекція точки на площину називаєть ся її ортогональною проекцією, якщо пряма, що ви значає напрям проектування, перпендикулярна до площини проекцій.
З теореми про дві паралельні прямі, одна з яких перпендику- лярна до площини (теорема 1 § 19) маємо, що кожна проектуюча пряма при ортогональному проектуванні перпендикулярна до площини проекцій.
Оскільки ортогональне проектування є окремим випадком паралельного проекту- вання, то воно має всі властивості останньо- го. Зокрема, ортогональною проекцією прямої
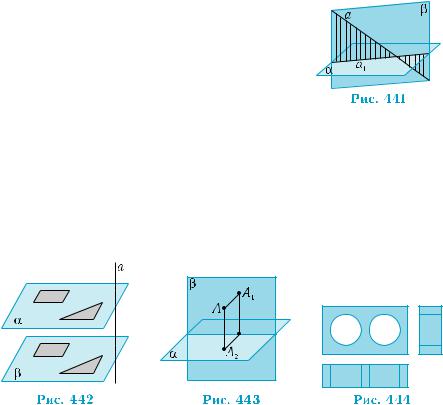
а на неперпендикулярну до неї площину α є пряма а1, яку можна вважати перетином пло- щини α з площиною β, складеної з проекту- ючих прямих (рис. 441). Ці проектуючі прямі
перпендикулярні до площини α. Тобто ортогональна проекція прямої на неперпендикулярну до неї площину є перетином пер- пендикулярних площин.
Ортогональне проектування має ряд особливостей. Opтoгoнaльномупроектуваннюнаплощинувідповідаєпоглядзго- ри на предмет, що розміщений на горизонтальному майданчику. Тому плоскі фігури, які розміщені паралельно площині проекцій, не спотворюються (рис. 442). Зокрема, не змінюються їхні лінійні
та кутові розміри, і ця властивість зумовлює широке використан- ня ортогонального проектування у технічному кресленні. Втім, оскільки проектування на одну площину, взагалі кажучи, не дає цілісного уявлення про предмет, то ортогональні проекції викону- ють принаймні на дві або й на три взаємно перпендикулярні пло- щини (рис. 443, 444). За таким кресленням нескладно відтворити
408 Розділ 4. Перпендикулярність прямих і площин
і форму предмета, і його розміри. Так, на рис. 444 представлені
фронтальна (вид спереду), горизонтальна (вид зверху) і профіль-
на (вид збоку) проекції деталі (пластини з двома отворами).
1) В яку точку трикутника ABC проектується вершина S? |
|
2) Визначити довжину відрізка, що з’єднує точку S з її проекцією |
|
на площину основи. |
|
1) Нехай при ортогональному проектуван- |
|
ні точка S проектується на точку О, SО ABC |
|
(рис. 446). Оскільки |
АО SO, то трикутник |
SАO — прямокутний з гіпотенузою SА. За тео- |
|
ремою Піфагора, AO = SA2 −SO2 . Аналогіч- |
|
но з прямокутних трикутників SСO і SВO має- |
|
мо: CO = SC2 −SO2 |
, BO = SB2 −SO2 . Але в |
правильній піраміді |
AS = CS = BS, тому AО = |
= CО = BО, тобто О |
— центр кола, описаного |
Ортогональне проектування, зазвичай, використовують і при |
|
зображенні кулі. В результаті зображенням кулі є круг. Якщо ж |
|
проектуючі прямі не перпендикулярні до площини проекцій, то проекцією кулі є частина площини, об-  межена еліпсом (уявіть собі тінь, яка прямує аж до горизонту, від кулі, що
межена еліпсом (уявіть собі тінь, яка прямує аж до горизонту, від кулі, що 
лежить на землі), що не відповідає на- шому уявленню про кулю (рис. 445).
Приклад 1. Правильна трикутна піраміда SABC з бічним ребром 5 см і
стороною основи 3 3 см ортогонально проектується на площину основи ABC.
навколо основи ABC. |
|
|
|
|
|
|
|
|
|
|
||||
2) Як відомо, радіус кола R, описаного навколо правильного три- |
||||||||||||||
кутника із стороною а, обчислюється за формулою: |
|
R = |
a 3 |
. Тому |
||||||||||
|
|
|||||||||||||
|
3 |
3 |
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
= 3 (см), а SO = |
|
2 |
|
2 |
|
2 |
2 |
= 4 (см). ■ |
|||||
AO = |
|
3 |
|
SA |
|
− AO |
|
= |
5 −3 |
|
||||
Відповідь. 2) 4 см. |
|
|
|
|
|
|
|
|
|
|
||||
Ортогональне проектування |
409 |
Поняття перпендикулярності прямої та площини породжує один із найважливіших видів симетрії у просторі, а саме: симетрію відносно площини.
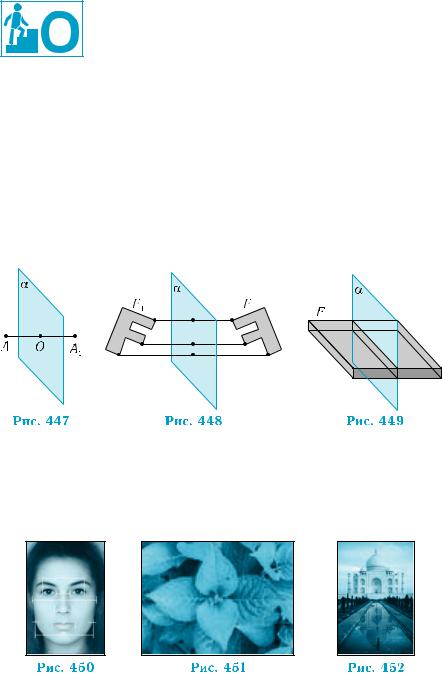
Точки А і А1 називаються симетричними відносно площини α, якщо відрізок АА1 перпендикулярний до площини α і точкою О перетину його з α поділяється навпіл (рис. 447). Точка площини α вважається симе
тричною сама собі.
Із цього означення випливає, що АО = ОА1, тобто точки А і А1 — центрально-симетричні відносно точки О.
Фігури простору F і F1 називаються симетричними відносно площини α, якщо для кожної точки одні
єї фігури є симетрична до неї точка в другій фігурі
(рис. 448).
Якщо ж у цьому означенні F = F1 (йдеться про ту саму фігуру),
то F називається симетричною відносно площини α (рис. 449).
Прикладами симетричних відносно площин фігур насичені як реальний фізичний простір, так і геометричний. Природа ство- рила симетричними фігури людей і більшості живих істот, симе-
410 |
Розділ 4. Перпендикулярність прямих і площин |
тричною є книга, яку ви тримаєте в руках, столовий посуд, праска і багато-багато ін. (рис. 450 – 452).
Неважко вказати площини, відносно яких симетричні куб, пра- вильна піраміда, куля тощо. Відшукання у геометричної фігури симетрій відносно площин є суттєвим кроком при її вивченні. Це суттєво полегшує знаходження і доведення її властивостей.
99 Контрольні запитання
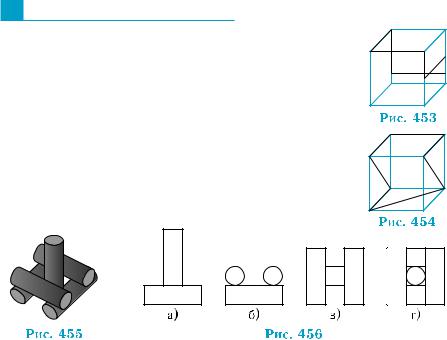
1.На рис. 453 зображено конструкцію, зроблену з дроту. Чи однакові її ортогональні проекції на площини нижньої грані і бічної грані каркасного куба?
2.На рис. 454 зображено конструкцію, зроблену з дроту. Порівняйте її ортогональні проекції на площини нижньої, верхньої і бічної граней кар- касного куба.
На рис. 455 зображено городошну фігуру «коло- дязь». На котрому з рис. 456, а)–г) зображено одну з ортогональних проекцій цієї фігури?
4.Чи може ортогональною проекцією квадрата бути прямокутник, який не є квадратом? А навпаки?
5.Чи правильно, що ортогональною проекцією довільної прямої є пряма?
6.Чи може відрізок бути ортогональною проекцією трикутника?
7.Чи правильно, що довжина ортогональної проекції відрізка менша або дорівнює довжині самого відрізка?
8.Чи обов’язково ортогональною проекцією квадрата є прямо- кутник?
9.Який кут може бути ортогональною проекцією прямого кута; гострого кута; тупого кута?
10.Відносно яких площин симетричні: а) точка; б) відрізок; в) пряма; г) площина?
Ортогональне проектування |
411 |
Графічні вправи
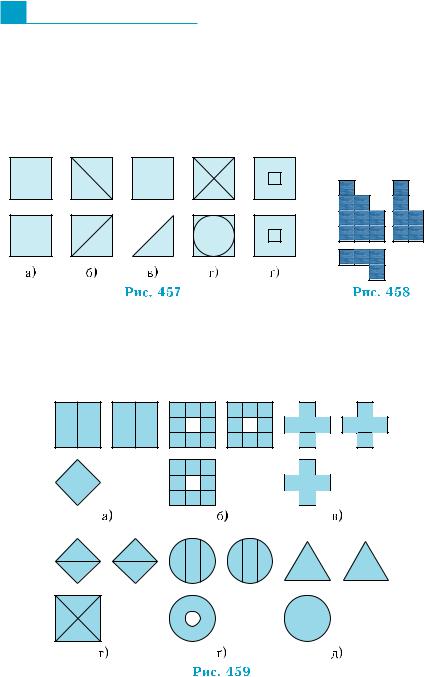
1.На кожному з рис. 457, а)–ґ) зображено вид спереду і вид звер- ху деякої фігури. Для кожної пари вкажіть тіло, яке може так виглядати (відсутність на рисунках штрихових ліній означає, що у відповідної фігури немає невидимих ребер, або вони за- криті видимими).
2.Скільки дерев’яних кубиків використано для побудови вежі, якщо з трьох боків вона виглядає, як на рис. 458?
3.Фігура задана на рис. 459, а)–д) за допомогою трьох ортого- нальних проекцій.
1)Зобразіть цю фігуру.
2)З’ясуйте, чи має фігура площини симетрії? Якщо має, то скільки?

412 |
Розділ 4. Перпендикулярність прямих і площин |
4.Побудуйте ортогональну проекцію правильної чотирикутної піраміди на:
1)площину основи;
2)площину, що проходить через ребро основи перпендику- лярно до площини основи.
Задачі
436°. Кінці відрізка АВ лежать по один бік від площини α. Від- стані кінців відрізка АВ до їхніх ортогональних проекцій А1, В1 на площину α дорівнюють 4 см і 8 см. Знайдіть:
1) довжину відрізка АВ, якщо А1В1 = 5 см; 2) відстань між серединою відрізка АВ і серединою симе-
тричного до нього відрізка відносно площини α.
437°. Кінці відрізка АВ лежать по різні боки від площини α. Від- стані кінців відрізка АВ до їхніх ортогональних проекцій А1, В1 на площину α дорівнюють 4 см і 8 см. Знайдіть:
1) довжину відрізка АВ, якщо А1В1 = 5 см; 2) відстань між серединою відрізка АВ і серединою симе-
тричного до нього відрізка відносно площини α.
438. У правильній чотирикутній піраміді SАВСD зі стороною основи а відстань між її вершиною S і симетричною до неї точкою S1 відносно площини АВСD дорівнює b. Знайдіть:
1) довжину бічного ребра піраміди;
2)площу перерізу піраміди, що проходить через протилежні бічні ребра.
439. Тільки одна зі сторін кута лежить у площині проекцій. Доведіть,щоортогональноюпроекцієюпрямогокутаєпрямий кут, гострого кута — кут, менший від проектованого, тупого кута—кут,більшийвідпроектованого,якщоплощина,вякій лежить кут, неперпендикулярна до площини проекцій.
440. Площина, паралельна основі правильної чотирикутної піраміди, поділяє бічне ребро навпіл. Зобразіть піраміду, симетричну даній відносно цієї площини. Зобразіть також фігуру, отриману об’єднанням даної і отриманої пірамід?
441. Три взаємно перпендикулярні прямі OX, OY, OZ визначають три площини α, β, γ. Точки М і N лежать у площинах β і γ. По- будуйте ортогональні проекції прямої MN на площини α, β, γ.
442. Балка закріплена кінцями на стінці і на стелі, причому відстані від кінців балки до лінії перетину стелі і стіни дорівнюють, відповідно, 30 см і 40 см. Знайдіть довжину
Ортогональне проектування |
413 |
балки, якщо довжина її проекції на лінію перетину стелі і стіни дорівнює 120 см.
Вправи для повторення
443.З точки А проведено до даної прямої дві рівні похилі АВ і АС, відстань між основами яких дорівнює 16 см. Визначте довжину проекції кожної похилої на дану пряму.
444.У трикутнику проекції бічних сторін на основу дорівнюють 15 м і 27 м, а більша з бічних сторін дорівнює 45 м. На які частини вона поділяється (починаючи від вершини) перпен- дикуляром до основи, проведеним з її середини.
У прямокутному трикутнику катети дорівнюють 13 см і 84 см. Визначте радіус вписаного кола.
Довжини трьох сторін прямокутної трапеції дорівнюють 25 см, 25 см, 32 см. Знайдіть довжину четвертої сторони.
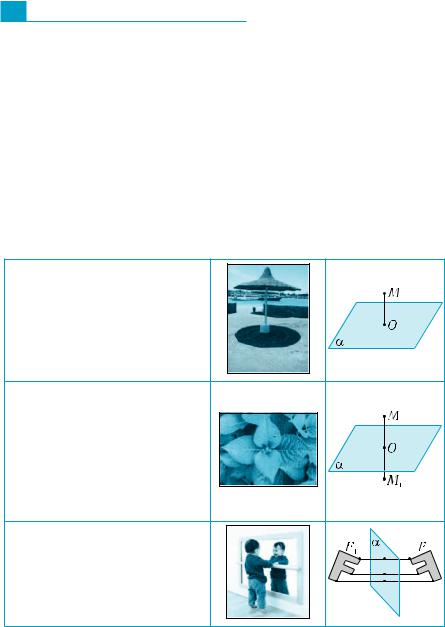
Підсумок
Головні означення
Паралельна проекція точки на площину називається її
ортогональною проекці єю, якщо пряма, що визначає напрям проектування, пер- пендикулярна до площини проекцій.
Точки М і М1 називаються
симетричними відносно площини α, якщо відрізок ММ1 перпендикулярний до α і точкою О перетину його з α поділяється навпіл.
Точка площини α вважається симетричною сама собі.
Фігури простору F і F1 на-
зиваються симетричними
відносно площини α, якщо для кожної точки однієї фігу- ри є симетрична до неї точка в другій фігурі.
