
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач

§11. Паралельність прямих і площин
Розглядається одне з важливіших відношень у стереометрії — паралельність прямої і площини, його властивості і застосування.
У попередніх параграфах було розглянуто відно- 
 шення паралельності прямих у просторі та його за-
шення паралельності прямих у просторі та його за-  стосування. He менш важливим як з теоретичного, так і з практичного погляду є відношення паралельності між прямими і площинами.
стосування. He менш важливим як з теоретичного, так і з практичного погляду є відношення паралельності між прямими і площинами.
Навколо себе ми бачимо безліч прикладів, які ілюструють взаємне розміщення прямих і площин (наприклад, взаємне розміщення стін, стелі, підлоги в кімнаті та ліній їхнього перетину, перекладини футбольних воріт і поверхні землі, ручки й аркуша паперу тощо, рис. 222 – 224).
Аналіз випадків взаємного розміщення прямої і площини з погляду наявності у них спільних точок дає такі варіанти розміщень.
1. Пряма і площина мають принаймні дві спільні точки. Тоді, згідно з аксіомою С1,
пряма належить площині.
13 Математика, 10 кл.
194 |
Розділ 2. Паралельність прямих і площин |
2. Пряма і площина мають єдину спільну точку. Можливість такого розміщення прямих і площин забезпечується тим, що поза площиною є точки простору. Довільна точ-
ка на площині i точка поза площиною ви-
значають пряму, що має з площиною одну спільну точку, тобто перетинає її.
3. Пряма і площина не мають спільних точок. У цьому разі їх називають пара-
лельними.
Пряма і площина, які не мають спільних точок, називаються паралельними.
Паралельність прямої а і площини α позначають звичним символом паралельності: a || α або α || a.
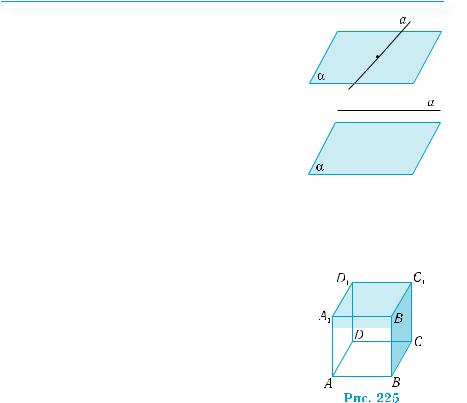
Користуючись означенням, можна встановити паралельність прямих і площин, пов’язаних з вершинами куба. Нехай дано
куб ABCDA1B1C1D1 (рис. 225). Пряма A1B1 паралельна площині ABCD. Справді, ця
пряма лежить у площині ABВ1А1. І якби
вона перетинала площину ABCD, то це було
б у точці, яка є спільною для площин ABCD і ABВ1А1. Але ж спільні точки цих площин
утворюють пряму АВ, яка паралельна прямій A1B1. Таким чином, пряма A1B1 не має спільних точок з площиною АВCD, тобто вона паралельна площині ABCD. Цей висновок стосується кожної прямої, яка містить ребро куба, і площини, яка містить грань куба, що не має спільних точок з цим ребром (B1C1 і ADD1A1, C1D1 і ABВ1А1 тощо).
Розглянутий спосіб обґрунтування паралельності прямої і площини можна узагальнити у такому твердженні.
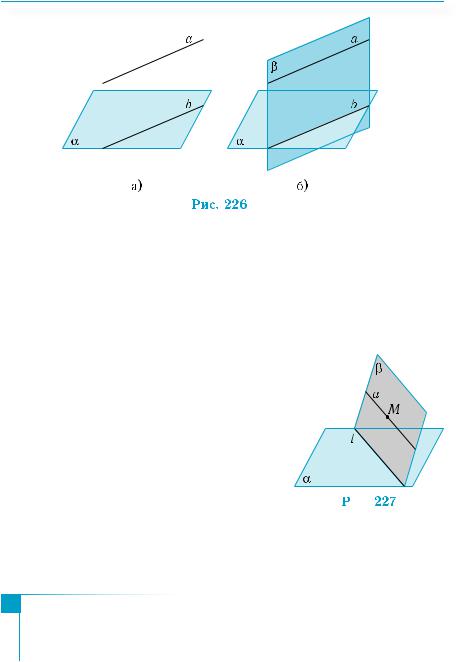
Теорема 1 (ознака паралельності прямої і площини).
Якщо пряма, що не лежить у даній площині, паралельна деякій прямій площини, то вона паралельна самій площині.
Нехай пряма а не лежить у площині α і паралельна прямій b цієї площини (рис. 226, а). Проведемо через прямі а і b площину β (рис. 226, б) (чому це можна зробити?). Площини α і β перети-
Паралельність прямих і площин |
195 |
наються по прямій b (збігатися вони не можуть за умовою). Тоді, якщо пряма а має спільну точку з площиною α , то ця точка знаходиться на прямій b. Але це суперечить умові, адже прямі а і b — паралельні. Тому пряма а не має спільних точок з площиною α, тобто пряма а і площина α — паралельні. ■
Задача 1. Через дану точку М, що не лежить в площині α, провести пряму, паралельну α.
Візьмемо в площині α довільну пряму l. Пряма l і точка М визначають деяку площину β. Проведемо у площині β через точку М пряму a, паралельну прямій l (рис. 227). Згідно з ознакою паралельності прямої і площини, пряма a i площина α — паралельні. ■
Зауважимо, що через точку М, що лежить поза площиною α, можна провести
нескінченну кількість прямих, паралель- 
 них даній площині. Це випливає, наприклад, з довільності вибору прямої l у розв’язанні задачі.
них даній площині. Це випливає, наприклад, з довільності вибору прямої l у розв’язанні задачі.
До речі, для довільної прямої а, паралельної площині α, існує нескінченна кількість прямих у площині α, які паралельні а.
!Надалі під паралельністю відрізка, променя площині (чи відрізка, променя — многокутнику тощо) розумітимемо паралельність відповідних прямих і площин, які визначаються даними фігурами.
13*
196 Розділ 2. Паралельність прямих і площин
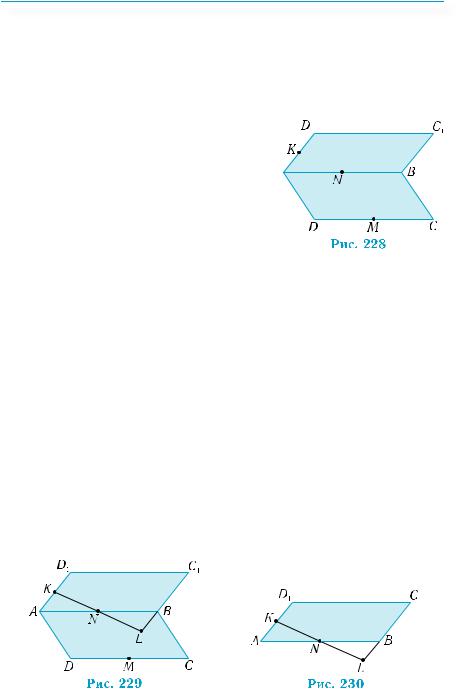
Приклад 1. ДвапаралелограмиАВСDiАВС1D1 лежатьурізних площинах, N, M i K — середини сторін АВ, CD i АD1 вiдповiдно. 1) Визначити взаємне розміщення прямих i площин:
C1D1 i ABC; KN i DD1C; D1B i MKN.
2) Побудувати точку перетину L прямої KN з площиною ВСС1. 3) Обчислити довжину вiдрiзка KL, якщо KN дорівнює 2 см.
Побудуємо рисунок, який відповідає умові (рис. 228).
1) Пряма C1D1 i площина ABC — па-
ралельні, за ознакою паралельності 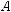 прямої і площини (теорема 1), адже
прямої і площини (теорема 1), адже
прямі C1D1 i AB — паралельні, за умо-
вою,прямаAB належитьплощиніABC, пряма C1D1 їй не належить.
Пряма KN перетинає площину DD1C. Справді, прямі СD i С1D1 — паралельні, за ознакою паралельності прямих (теорема 2 §8). Тому пряма C1D1 належить площині DD1C (чому?). У площині АВС1D1 прямі KN i С1D1 перетинаються. Таким чином, пряма KN має спільну точку з площиною DD1C.
Пряма D1B паралельна площині MKN. Справді, відрізок KN є середньою лінією трикутника АD1В. Тому пряма KN паралельна прямій D1В. Оскільки пряма D1В не лежить у площині MKN, то, за ознакою паралельності прямої і площини (теорема 1), пряма D1В паралельна площині MKN.
2) Пряма KN лежить у площині АВС1. Тому точка її перетину з площиною ВСС1 лежить на лінії перетину площин АВС1 і ВСС1, тобто на прямій ВС1.
Побудова. Знаходимо точку перетину прямих KN і ВС1 у площині АВС1, це і є шукана точка L (рис. 229).
3) Для обчислення довжини вiдрiзка KL зобразимо побудову на площині АВС1D1 (рис. 230). Розглянемо трикутники АKN і BLN. Вони рівні, за ознакою рівності трикутників: АN = BN, за умовою,
Паралельність прямих і площин |
197 |
АKN = BLN як внутрішні різносторонні кути при паралельних AK і BL та січній KL, KNА = BNL як вертикальні кути. Звідси
NL = KN = 2 (см). Тому KL = KN + NL = 4 (см). ■
Відповідь. 3) 4 см.
Розглянемо твердження, обернене до ознаки паралельності прямої і площини. Для цього необхідно
поміняти умову і висновок цієї теореми.
Теорема 2 (обернена до ознаки паралельності прямої і площини).
Якщо пряма паралельна площині, то в цій площині існує пряма, яка паралельна даній прямій.
Ця теорема є властивістю відношення паралельності прямої і площини. Наочно правильність наведеного твердження очевидна. Логічна її обґрунтованість випливає з наступної теореми, яка і сама корисна при розв’язуванні багатьох задач.
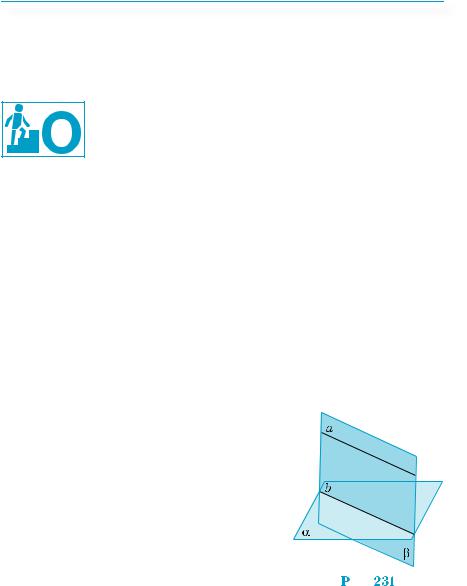
Теорема 3 (про лінію перетину площин, одна з яких проходить через пряму, паралельну другій).
Якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то лінія їхнього перетину паралельна даній прямій.
Нехай пряма а паралельна площині α, а площина β містить пряму а і перетинає площину α по прямій b (рис. 231). Прямі a і b лежать в одній площині, за побудовою. Вони не мають спільних точок, бо тоді пряма a мала б спільні точки з площиною α. А, за умовою, пряма a паралельна площині α. Тому прямі а і b — паралельні. ■
Тепер зрозуміло, як довести теорему 2.
Через дану пряму, паралельну площині 
 α, слід провести площину, яка перетинає площину α. Для цього
α, слід провести площину, яка перетинає площину α. Для цього
достатньо взяти в площині α довільну точку і через пряму а та обрану точку провести площину.
198 Розділ 2. Паралельність прямих і площин
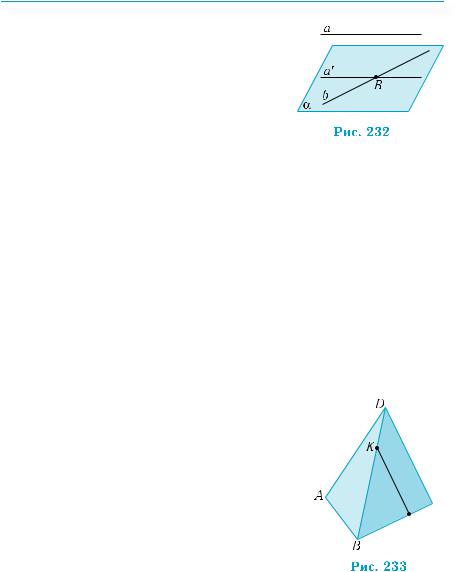
Задача 2. Провести через одну з двох мимобіжних прямих площину, паралельну іншій прямій.
Нехай а і b — мимобіжні прямі. Проведемо через довільну точку В прямої b пряму а′, паралельну прямій а (рис. 232). Прямі а′ і b визначають площину α, яка, за ознакою паралельності прямої і площини, паралельна прямій а. ■
Приклад 2. У правильному тетраедрі DABC, усі ребра якого дорівнюють 6 см, точка K лежить на ребрі DB, і DK = 2 см. Точка M лежить на ребрі BC, і BM = 4 см. Точка P — середина AB.
1) Довести, що пряма KM паралельна площині ADC. 2) Довести, що пряма PM перетинає площину ADC.
3) Провести через точку P пряму, паралельну площині ADC, яка перетинає медіану BL трикутника BDC.
4) Побудувати переріз тетраедра площиною, яка проходить через точки Р і K паралельно прямій АС.
5) Провести через центр грані BDC пряму, паралельну площинам ABD і ACD, і знайти довжину найбільшого відрізка цієї прямої, який належить тетраедру.
Побудуємо рисунок, який відображає умову завдання
(рис. 233).
1) З умови випливає, що точки K і M поді-
ляють сторони BD і BC трикутника BDC в однаковому відношенні, рахуючи від вершини В. За теоремою, оберненою до теореми Фалеса,
пряма KM паралельна прямій DC. А тоді, за
ознакою паралельності прямої і площини (тео- 
 рема 1), пряма KM паралельна площині ADC.
рема 1), пряма KM паралельна площині ADC. 

2) Точки P і M поділяють сторони BА і BC
трикутника AВC у різних відношеннях, раху-
ючи від вершини В. З теореми Фалеса випли-
ває, що пряма PM перетинає пряму AC. А це означає, що вона перетинає і площину ADC.
3) Розглянемо трикутник АBL (рис. 234), де L — середина CD. Точка P є серединою сторони AB, а точка Е — серединою сторони BL, відрізок РЕ є середньою лінією трикутника АBL. Тому пряма РЕ паралельна прямій АL, яка лежить у площині ADC. За
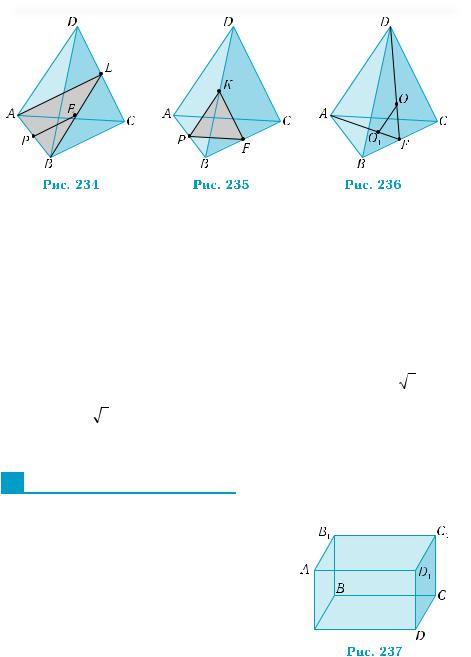
Паралельність прямих і площин |
199 |
ознакою паралельності прямої і площини (теорема 1), пряма РЕ |
|||||
паралельна площині ADC і перетинає медіану BL трикутника |
|||||
BDC. |
|
|
|
|
|
4) Проведемо через точку Р пряму, паралельну прямій AC, |
|||||
і позначимо її точку перетину зі стороною BC через F (рис. 235). |
|||||
Трикутник PKF |
є шуканим перерізом. |
|
|
||
5) Нехай О — центр грані BDC (рис. 236). У трикутнику ADF, де |
|||||
F — середина BC, проведемо пряму ОО1, паралельну прямій AD. |
|||||
ТодіпрямаОО1 будепаралельноюплощинамABD іACD,заознакою |
|||||
паралельностіпрямоїіплощини.ТрикутникиADF |
іОО1F |
—подібні. |
|||
Тому |
OO1 = |
OF |
. З умови маємо: AD = 6 см, |
DF = |
3 3 см, |
|
AD |
FD |
|
|
|
|
1 |
3 |
см. Звідси: ОО1 = 2 см. ■ |
|
|
OF = |
3 DF = |
|
|
||
Відповідь. 5) 2 см. |
|
|
|||
Контрольні запитання
1. На рис. 237 зображено прямокутний паралелепіпед ABCDA1B1C1D1.
1) У площинах яких граней паралелепіпеда лежить пряма CC1?
2) З площинами яких граней паралеле-  піпеда перетинається пряма A1D?
піпеда перетинається пряма A1D?
3) Площинам яких граней паралелепі-
педа паралельна пряма BC?
4)ЯкрозміщенідіагоналіграніA1B1C1D1 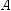 відносно площини ABCD?
відносно площини ABCD?
200 |
|
Розділ 2. Паралельність прямих і площин |
|||||
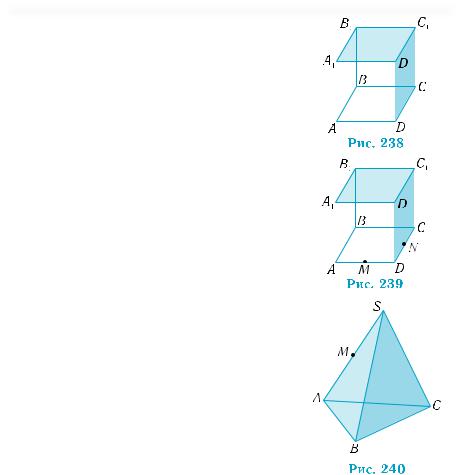
2. |
Скільки існує площин, паралельних ре- |
||||||
|
бру ВВ1 куба ABCDA1B1C1D1 (рис. 238) |
|
|||||
|
і таких, що проходять через: |
|
|||||
|
1) |
вершину D; |
|
|
|
|
|
|
2) |
ребро DС; |
|
|
|
|
|
|
|
|
|
|
|||
|
3) |
діагональ грані AС; |
|
|
|
|
|
|
4) діагональ куба A1С? |
|
|
|
|
||
|
|
|
|
|
|||
3. |
Куб ABCDA1B1C1D1 (рис. 239) перетина- |
||||||
|
ється площиною, що проходить через се- |
||||||
|
редини M, N ребер АВ і ВС паралельно |
|
|
||||
|
|
||||||
|
ребру DD1. |
|
|
||||
|
1) |
Який многокутник отримано у пере- |
|
|
|
|
|
|
|
|
|
|
|
||
|
різі? |
|
|
|
|
|
|
|
2) |
Чому дорівнює периметр перерізу, |
|
|
|
|
|
|
якщо ребро куба дорівнює а? |
|
|
|
|
|
|
4. |
УправильномутетраедріSABC (рис.240) |
||||||
|
площина α проходить через середину М |
||||||
|
ребраAS паралельнопрямійСS.Чиможе |
||||||
|
переріз тетраедра площиною α бути: |
||||||
|
1) |
трикутником; |
|||||
|
2) |
правильним трикутником; |
|||||
|
3) |
чотирикутником; |
|||||
|
4) |
ромбом? |
|||||
5. |
Відомо, що пряма паралельна площині. |
||||||
|
Чи паралельна вона кожній прямій цієї |
||||||
|
площини? |
||||||
6. |
Чи правильно, що діагональ грані куба |
||||||
|
паралельна протилежній грані куба? |
||||||
7. |
Чи можуть перетинатися площини, паралельні одній і тій са- |
||||||
|
мій прямій? |
||||||
8. |
Чи правильно, що через точку поза площиною можна провес- |
||||||
|
ти лише одну пряму, паралельну даній площині? |
||||||
9. |
Пряма мимобіжна з деякою прямою, що лежить у даній пло- |
||||||
|
щині. Чи може вона бути паралельною цій площині? |
||||||
10. |
Чи може площина, що проходить через середини двох сторін |
||||||
|
трикутника, перетинати його третю сторону? |
||||||
Паралельність прямих і площин |
201 |
Графічні вправи
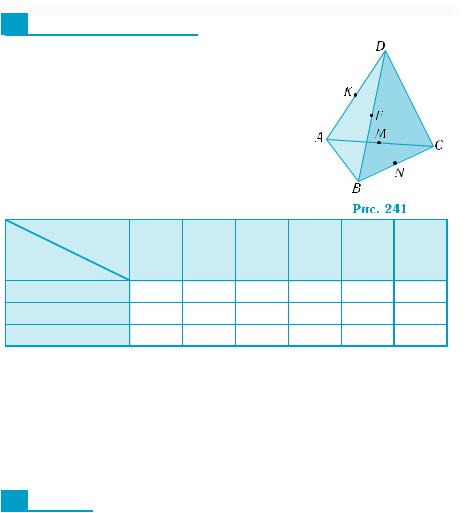
1. На рис. 241 зображено тетраедр ABCD, точки K, F, M, N — середини відповідних ребер. Заповніть за наведеним зразком таблицю, вибравши необхідне розміщення прямих l і площин α.
l і α
Взаємне
розміщення
l × α l || α
l α
DB |
MN |
KC |
MN |
KF |
CF |
і AMN |
і ABC |
і DMN |
і ABD |
і DMN |
і ADN |
+ |
|
|
|
|
|
2.Побудуйте рисунок за наведеними даними.
1)Пряма АВ паралельна площині α, а площина АВС перетинає площину α по прямій CD.
2)Пряма а паралельна кожній з площин α і β, що перетинаються.
3)ПлощинапроходитьчерезвершиниВ,D1 кубаABCDA1B1C1D1 паралельно ребру CD.
Задачі
190. Трикутник АВС i паралелограм АВFD лежать у різних площинах, M, N, K — середини сторін АС, ВС, ВF вiдповiдно. 1°) Визначте взаємне розміщення прямих i площин: DF
i АВС; АВ i MNK; АС i DВF; МК i ВСD.
2°) Побудуйте точку Р перетину прямої BD з площиною АСF. 3) Обчисліть довжину вiдрiзка РK, якщо МN = 3 см.
4) Побудуйте пряму, паралельну площинам трикутника i паралелограма.
191. Ромб АВСD i прямокутник DВЕF лежать у різних площинах; M, N, K — середини сторін АD, АВ, EF вiдповiдно.

202 |
|
Розділ 2. |
Паралельність прямих і площин |
|
1°) Визначте взаємне розміщення прямих i площин: EF |
||
|
i АВС; МС i DЕF; МN i СFЕ; ВЕ i АDF. |
||
|
2°) Побудуйте точку Р перетину прямої МN з площиною ВСЕ. |
||
|
3) |
Обчисліть довжину вiдрiзка ЕF, якщо МN = 4 см. |
|
|
4) |
Побудуйте пряму, паралельну площинам ромба i прямо- |
|
|
кутника. |
|
|
192. |
Дано куб АВСDА1В1С1D1. |
|
|
|
1°) Визначте взаємне розміщення прямої CD і площин АВС, |
||
|
АВВ1, AA1D. |
|
|
|
2°) Доведіть, що пряма АВ1 паралельна площині CDD1. |
||
|
3) |
Через середину ребра A1D1 проведіть пряму, паралельну |
|
|
площинам АА1В і СС1В1. |
|
|
|
4°) Побудуйте пряму, що перетинає площини тільки чоти- |
||
|
рьох граней куба. |
|
|
|
5) |
Побудуйте лінію перетину площин ADC1 i A1D1C. |
|
|
6) |
Знайдіть кут між прямими А |
В і В С. |
193. |
|
1 |
1 |
Дано чотирикутну піраміду SABCD, в основі якої лежить |
|||
|
трапеція ABCD, ВС||AD. |
|
|
|
1°) Визначте взаємне розміщення прямої AD і площини BCS. |
||
|
2) |
Через середину ребра АS проведіть пряму, паралельну |
|
|
площинам АВС i BCS. |
|
|
|
3°) Побудуйте пряму, що перетинає площини тільки двох |
||
|
бічних граней. |
|
|
|
4*) Побудуйте лінію перетину площин, які містять проти- |
||
|
лежні бічні грані, що проходять через основи трапеції. |
||
194. Точка В лежить у площині α, а відрізок CD завдовжки 12 см |
|||
|
паралельний цій площині. Точка А лежить на відрізку ВС |
||
|
і ВА : AC = 4 : 3. |
|
|
|
1°) Побудуйте точку Р перетину прямої AD з площиною α. |
||
|
2°) Визначте взаємне розміщення прямих ВР і CD. |
||
|
3) |
Знайдіть довжину відрізка ВР. |
|
195. Трапеція ABCD лежить у площині α. Її основа ВС дорівнює |
|||
|
12 см. Точка М лежить поза площиною α, а точка K — сере- |
||
|
дина відрізка ВМ. |
|
|
|
1) Побудуйте точку N перетину площини ADK і відрізка МС. |
||
|
2) |
Визначте взаємне розміщення прямої KN і площини α. |
|
|
3) |
Знайдіть довжину відрізка KN. |
|

Паралельність прямих і площин |
203 |
196. Точка М не лежить у площині прямокутника ABCD. Доведіть, що пряма СD паралельна площині трикутника АВМ.
197. Площина α паралельна стороні ВС трикутника АВС і проходить через середину сторони АВ. Доведіть, що площина α проходить через середину сторони АС.
198. Доведіть, що дві площини перетинаються, якщо:
1) через точку, яка не належить цим площинам, можна провести лише одну пряму, паралельну даним площинам; 2) одна із площин перетинає пряму, паралельну другій площині.
199. Побудуйте пряму, яка проходить через дану точку і паралельна двом даним площинам, що перетинаються.
200. Проведіть через дану точку простору площину, паралельну двом даним мимобіжним прямим.
201. Дано трикутну піраміду SABC. Побудуйте точку перетину площини ABC з прямою MN, якщо:
1°) точки M і N лежать на ребрах SC і SB;
2) точка M лежить на ребрі AS, а точка N — на грані BSC; 3*) точка M лежить на грані ABS, а точка N — на грані ASC.
202. Через центр грані AA1D1D куба ABCDA1B1C1D1 проведено дві прямі, паралельні прямим D1D і B1C відповідно.
1) Знайдіть кут між цими прямими.
2) Визначте взаємне розміщення побудованих прямих і пло-
щин BB1C1C та DD1C1C.
203. Дано куб ABCDA1B1C1D1. Побудуйте переріз куба площиною, яка проходить через:
1°) вершини A, B, C1;
2°) вершини B, D і середину ребра AA1;
3°) середину ребра CD паралельно площині ADC1; 4°) центр грані CDD1C1 паралельно площині ADD1; 5) вершину A і середини ребер CC1 і C1D1;
6*) відрізок, який з’єднує середини ребер AA1 і B1C1, паралельно площині AB1C.
204. Дано тетраедр SABC і точку F на ребрі AB, яка поділяє відрізок AB у відношенні 3:1 (AF : FB).
1) Побудуйте переріз тетраедра площиною, яка проходить через вершину C, середину ребра AS і паралельна прямій BS. 2*) У якому відношенні побудований переріз ділить відрізок, що з’єднує точку F і середину відрізка AC?
204 |
Розділ 2. Паралельність прямих і площин |
Вправи для повторення
205.Маємо паралелепіпед ABCDA1B1C1D1.
1)Вкажіть дві прямі, паралельні площині ABC, що проходять через одну точку.
2)Побудуйте площину, яка перетинає площину ABC і містить нескінченну кількість прямих, паралельних площині ABC. 3*) Чи можуть перетинатися площини ABC і A1B1C1?
206.Нехай прямі а і b перетинаються. Побудуйте площину, що проходить через дану точку простору паралельно як прямій а, так і прямій b.
Підсумок
Головне означення
Пряма і площина, які не мають спільних точок, називаються па-
ралельними. |
|
|
a || α. |
|
|
|
|
|
|
|
|
Головні твердження |
||
Ознака |
пара- |
Якщо пряма, що не ле- |
|
|
лельності пря- |
жить у даній площині, |
|
||
мої і площини |
паралельна деякій пря- |
|
||
|
|
мій площини, то вона |
|
|
|
|
паралельна самій пло- |
b α,a || b a || α |
|
|
|
щині. |
|
|
Теорема, |
обер- |
Якщо пряма паралель- |
|
|
нена до ознаки |
на площині, то в цій |
|
||
паралельності |
площині існує |
пряма, |
|
|
прямої |
і пло- |
яка паралельна |
даній |
|
щини |
|
прямій. |
|
a || α b: b α, b || α |
|
|
|
|
|
Теорема про лі- |
Якщо площина |
прохо- |
|
|
нію перетину |
дить через пряму, пара- |
|
||
площин, |
одна з |
лельну іншій площині |
|
|
яких проходить |
і перетинає цю площину, |
|
||
через пряму, па- |
то лінія перетину пара- |
|
||
ралельну другій |
лельна даній прямій. |
a || α,a β,b =α ∩ β a || b |
||
|
|
|
|
|
