
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач
§13. Тригонометричні функції числового аргументу
У цьому параграфі будуть визначені тригонометричні функції для довільного числового аргументу. ×асто положення рухомих об’єктів, наприклад, небесних тіл, визначають за допомогою кутів, зокрема, кутів обертання. Тому функції, що описують їхній рух, нерідко своїм аргументом мають міру кута. Отже, доцільно узагальнити поняття кута та докладніше обговорити питання про його вимірювання.
1. Радіанне вимірювання кутів
Відомо, що у планіметрії розглядають кути, градус- 
 на міра яких знаходиться у проміжку від 0° до 180°.
на міра яких знаходиться у проміжку від 0° до 180°.  Але на практиці доводиться розглядати кути, міра яких більша від 180°.
Але на практиці доводиться розглядати кути, міра яких більша від 180°.
Наприклад, літак з пункту А має перелетіти у пункт В. Курс літака визначають за допомогою кута між напрямом лінії польоту і напрямом меридіана
«південь – північ», який відлічують про- 
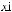
 ти руху годинникової стрілки (рис. 262).
ти руху годинникової стрілки (рис. 262).
Отже, при розв’язуванні таких задач доводиться вже розглядати кути в проміжку від 0° до 360°.
У геометрії кути розглядаються як фігури, утворені за допомогою двох про-
менів, що мають спільний початок. Промені називаються сторонами кута, їхня спільна точка – вершиною кута.
Тепер, розглядаючи кут, покажемо, як ця фігура утворилася: один з променів будемо розглядати як нерухомий, а другий промінь — як такий, що рухався від початкового положення, в якому
15*
228 Розділ 3. Тригонометричні Функції
він суміщався з нерухомою стороною. Цю другу сторону ми нази-
ватимемо рухомою і вважатимемо, що кут утворюється обертан-
ням рухомого променя навколо вершини кута. Одержані при цьому кути називають кутами обертання.
На рис. 263 зображено кут, утворений обертанням рухомого променя ОА1 навколо точки О, з нерухомим променем ОА. Траєкторією
руху точки А1 променя ОА1 є лінія AА1. Вона є дугою кола з центром у точці О і з радіусом ОА1 (або ОА). Отже, точка рухається по дузі кола з
радіусом R = ОА.
Зазвичай кути в геометрії вимірюють в градусах: 1 градус
(1°) — це |
1 |
частина міри прямого кута, або |
|
1 |
частина міри |
|
90 |
180 |
|||||
|
|
|
||||
розгорнутого кута. Кути обертання теж можна вимірювати в градусах. Але деколи більш зручною є інша міра.
При обертанні фіксована точка рухомого променя описує дугу кола з центром у вершині кута
(рис. 264). Вимірювання кутів обертання можна замінити вимірюванням довжини дуги кола. Щоб виключити вплив величини радіуса, мірою
кута вважають не довжину дуги l, а відношення
цієїдовжинидорадіусаR.Такаміраназивається
радіанною.
!Відношення шляху, пройденого точкою А, до радіуса R не залежить від радіуса. Тому це відношення може бути прийнято за міру кута обертання.
Радіанною мірою кута обертання називається відношення шляху, пройденого від початкового положення фіксованою точкою рухомого променя, до відстані від цієї точки до початку променя.
Чисельно радіанна міра кута обертання дорівнює шляху, яке пройде точка рухомого променя, що знаходиться на одиничній відстані від вершини.
За одиницю при радіанному вимірюванні 
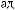
 кута обертання приймають міру кута, що спи-
кута обертання приймають міру кута, що спи- 
Тригонометричні функції числового аргументу |
229 |
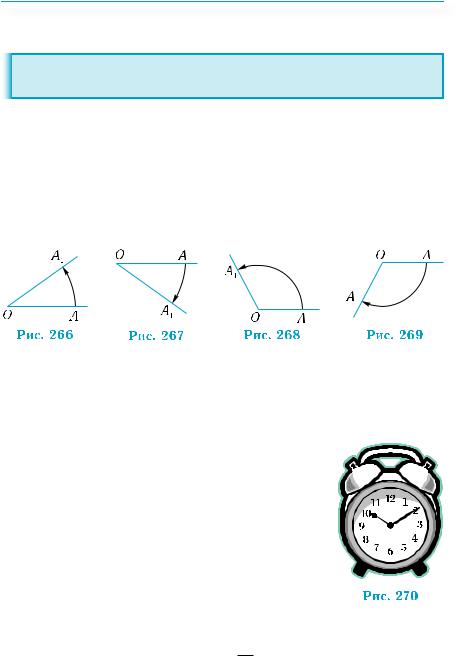
рається на дугу, довжина якої дорівнює довжині радіуса (рис. 265). Ця одиниця називається радіаном.
Термін “радіан” походить від латинського radius — радіус.
Рух точки по колу багато у чому схожий з рухом точки по прямій. Щобвизначитиположенняточкинапрямій,недостатньознатишлях, пройденийнеювідпочатковоїточки,—потрібновказатищенапрям руху. Зазвичай на прямій фіксують додатний напрям, а положення точки визначається одним числом, додатним чи від’ємним.
Обертання рухомого променя навколо вершини кута можливе в двох протилежних напрямах. Геометрично два кути на рис. 266–267 є рівними, але як кути обертання їх слід вважати за різні.
При обертанні на площині будемо вважати додатним напрямомобертаннянапрямпротирухугодинниковоїстрілки(рис.268). Обертання за годинниковою стрілкою будемо вважати від’ємним (рис. 269). Відповідно, кути, що утворюються такими обертаннями, будемо вимірювати додатними і від’ємними числами.
Наприклад, годинник на рис. 270 показує 10 хвилин на одинадцяту, або 50 хвилин до одинадцятої години. Тут обертання хвилинної стрілки вимірюється або від’ємним кутом (за
годинниковою стрілкою), або додатним, тільки вибір напряму ми позначаємо не знаком мінус чи плюс, а словами «10 хвилин на одинадцяту»
і «50 хвилин до одинадцятої».
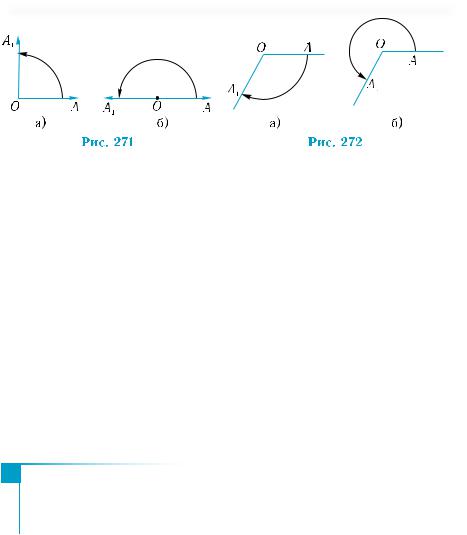
Кут в 90° одержимо, якщо промінь ОА1 здійснить чверть повного оберту навколо точки О проти годинникової стрілки (рис. 271, а); результатом
півоберту променя ОА1 проти годинникової стрілки є кут 180°
(рис. 271, б). Кут (–150°) — це 150360 = 125 повного оберту променя ОА1 навколо точки О за годинниковою стрілкою (рис. 272, а).
230 |
Розділ 3. Тригонометричні Функції |
Кути обертання мають важливу особливість: їхні кутові міри
можуть перевищувати 180°. Рухомий промінь з початком у фіксо-
ваній точці може знаходитись у будь-якому положенні на площи-
ні (рис. 272, б).
Якщо кутова міра кута становить α радіан, α > 0, то це означає, що довжина відповідної дуги кола l з радіусом R дорівнює αR, тобто l = αR.
Звідси випливає, що довжина дуги одиничного кола чи-
сельно збігається з радіанною мірою відповідного кута.
Власне, саме ця обставина і робить радіанну міру кута зручною. |
|||||||||||||
|
Коло радіуса R має довжину 2πR |
. Розглянемо дугу, довжина |
|||||||||||
якої дорівнює радіусу R. Її довжина в |
2π разів менша від довжини |
||||||||||||
кола. Тому кут, що дорівнює 1 |
радіану (скорочено: рад), становить |
||||||||||||
|
1 |
|
|
|
|
|
|
|
360° |
|
180° |
′ ′′ |
|
|
2π частини повного оберту: 1 |
рад = |
|
2π |
= |
π |
|||||||
|
|
≈ 57°17 45 . |
|||||||||||
|
Оскільки радіанна міра кута 360° становить 2π рад, то 1° від- |
||||||||||||
повідає |
2π |
= |
|
π |
≈ 0,017 рад. |
|
|
|
|
|
|||
|
180 |
|
|
|
|
|
|||||||
360 |
|
|
|
|
|
|
|
|
|||||
!Цим самим встановлено зв’язок між радіанною і градусною мірами кута, який, до речі, свідчить про незалежність радіанної міри кута від вибору фіксованої точки рухомого променя.
Ïðèê ëàä |
1. |
Виразити кути: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1) 30°, 45°, 60°, –150° у радіанній мірі; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2) |
2π |
; |
|
3π |
; |
5π |
|
; − |
|
4π |
у градусній мірі. |
|
|
|
|
|
|
|
|
||||||||||
|
4 |
|
6 |
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
π ; |
|
|
π |
|
π ; |
|||||||
1) Оскільки 1° = |
|
|
, то 30° = |
|
30 = |
45° = |
|
45 = |
|||||||||||||||||||||
180 |
180 |
180 |
|||||||||||||||||||||||||||
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
π |
|
|
5π . |
6 |
|
|
4 |
||||||||
60° = |
|
|
60 = |
; −150° = |
|
(−150) = − |
|
|
|
|
|
|
|||||||||||||||||
180 |
3 |
180 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||||||

Тригонометричні функції числового аргументу |
231 |
2)Оскільки1рад= 180° ,то |
2π |
= |
180° |
2π |
=120° ; 3π |
= 180° |
3π = |
|||||||||||||||||
|
5π |
|
180° |
|
5π |
|
π |
|
|
3 |
|
π |
|
|
|
3 |
|
|
4 |
π |
4 |
|||
= 135°; |
= |
|
=150°; |
− |
4π |
= |
180° |
|
|
− |
4π |
= −240°. |
|
|||||||||||
6 |
|
π |
|
6 |
3 |
π |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||
Відповідь. 1) |
|
π ; |
π ; |
π; − |
|
5π |
; 2) 120°, 135°, 150°, –240°. |
|
||||||||||||||||
|
6 |
|
||||||||||||||||||||||
|
|
|
|
|
|
6 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Радіанною мірою дуги кола зазвичай називають ра- |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
діанну міру відповідного центрального кута. Так, |
||||||||||||||||||||
|
|
|
|
радіанні міри дуг AA1, зображених на рис. 272, а), б), |
||||||||||||||||||||
|
|
|
|
відповідно дорівнюють |
π |
, π . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Радіанна міра одиничного кола дорівнює його довжині, тобто |
||||||||||||||||||||||||
числу 2π, радіанна міра одиничного півкола дорівнює числу |
π; ра- |
|||||||||||||||||||||||
діанна міра чверті одиничного кола становить |
π . |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Слово «радіан» часто пропускають і кажуть «кут π». Так, записи |
||||||||||||||||||||||||
α = 1,12; α = 0,39; |
α = 15,7 означають, що кут |
α виміряний у ра- |
||||||||||||||||||||||
діанах. Водночас позначення градусів не прийнято пропускати в записах.
Введення радіанної міри кута обертання дає змогу встановити простий зв’язок між кутовою і лінійною швидкостями точки, яка перебуває у рівномірному обертальному русі. Кутова швидкість при рівномірному обертанні — це кут, на який повертається точка за одиницю часу. Вона зазвичай вимірюється в радіанах за секунду (рад/с). Лінійна швидкість точки при рівномірному русі — це відстань, на яку переміщується точка по траєкторії руху за одиницю часу.
Ïðèê ëàä 2 . Точка рівномірно рухається по колу, радіус якого R = 40 см, з лінійною швидкістю v = 80 см/с. Знайти кутову швидкість точки.
За одну секунду точка проходить шлях, що дорівнює 80 см. Треба знайти міру кута, на який обертається точка за 1 с. Із визначення радіана випливає, що куту в 1 рад відповідає дуга, довжина якої дорівнює довжині радіуса. Оскільки довжина шляху, який проходить точка за 1 с, вдвічі більша від радіуса, то відповідна дуга кола відповідає куту в 2 рад.
Відповідь. 2 рад/с.

232 Розділ 3. Тригонометричні Функції
Використовуючи від’ємні міри кутів, можна модуль міри будь-
якого кута, в межах повного оберту, звести до числа, що не переви-
щує півоберту. Наприклад, при градусному вимірюванні кутів замість проміжку 0° ≤ α ≤ 360° можна завжди розглядати кути в проміжку–180° ≤ α ≤ 180°,прирадіанномувимірюваннізамістьпроміжку 0 ≤ α ≤ 2π — розглядати проміжок −π ≤ α ≤ π. Так, замість
кута 225° можна розглядати кут –(360° – 225°) = –135°; замість кута
5π |
|
2π − |
5π |
= − |
π |
. |
3 |
— кут – |
|
3 |
|||
|
|
3 |
|
|
||
|
В географії, астрономії, де застосовується градусна система ви- |
|||||
мірювання кутів, послуговуються також меншими одиницями ви-
мірювання: 601° =1′(кутова мінута), 601′ =1′′ (кутова секунда). Градусною мірою кута послуговуються в оптичних приладах.
Мінута — від латинського minuta — зменшена (частка), від minuo — зменшую, розбиваю на дрібні частини.
Секунда — від латинських secunda (division gradi) —
друге (ділення градуса), secundus — наступний.
У техніці за одиницю вимірювання кутів приймають повний
оберт, у військовій справі — «тисячну», тобто |
1 |
частину |
|
3000 |
|||
|
|
розгорнутого кута, чи велику поділку кутоміра, яка дорівнює
100 «тисячним». У мореплавстві одиницею вимірювання є румб,
що дорівнює 1 частині повного оберту.
32
Контрольні запитання
1°. Чи можна здійснити поворот годинникової стрілки на: а) 270°;
б) 360°; в) 450°; г) –60°; ґ) –290°; д) –512°?
2°. Чому дорівнюють у радіанах величини кутів: а) правильного трикутника; б) прямокутного рівнобедреного трикутника?
3°. Чому дорівнює радіанна міра кута АОВ, зображеного на рис. 273, якщо довжина
дуги MN дорівнює 0,5ON?
Тригонометричні функції числового аргументу |
233 |
4.Чому дорівнює у градусній мірі кут оберту маховика, що зробив за годинниковою стрілкою: 1) 1 оберт; 2) 1,5 оберту?
Які кути описують хвилинна і годинна стрілки за: 1) 20 хв; 2) 5 год?
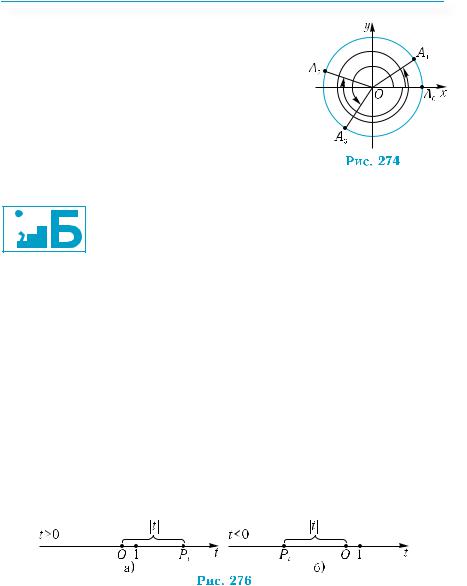
Чому дорівнюють наближено градусні і радіанні міри кутів обертання, позна-
чених стрілками на рис. 274.5.6.
2. Тригонометричне коло
Як відомо, між дійсними числами і точками коорди- 
 натноїпрямоїіснуєвзаємнооднозначнавідповідність.
натноїпрямоїіснуєвзаємнооднозначнавідповідність.  Уявімо собі, що точка рухається по координатній прямій від початку координат. Якщо вона рухається у додатному напрямі і пройде відстань, що дорівнює трьом одиницям виміру довжини, то вона потрапить у точку А(3) (рис. 275). Якщо ж вона рухається у напрямі, протилежному до напряму координатної прямої, і пройде ту саму відстань, то вона потрапить у точку В(–3) (див. рис. 275). Зверніть увагу на те, що в обох випадках від-
Уявімо собі, що точка рухається по координатній прямій від початку координат. Якщо вона рухається у додатному напрямі і пройде відстань, що дорівнює трьом одиницям виміру довжини, то вона потрапить у точку А(3) (рис. 275). Якщо ж вона рухається у напрямі, протилежному до напряму координатної прямої, і пройде ту саму відстань, то вона потрапить у точку В(–3) (див. рис. 275). Зверніть увагу на те, що в обох випадках від- 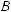

 стань, пройдена точкою, дорівнює модулю ко-
стань, пройдена точкою, дорівнює модулю ко-  ординати точки, в яку вона потрапляє.
ординати точки, в яку вона потрапляє. 



Взагалі, нехай маємо довільне число t. Вважатимемо, що точка рухається вздовж прямої, причому в додатному напрямі, якщо t > 0, і у від’ємному напрямі, якщо t < 0. Коли пройдена відстань дорівнюватиме |t|, точка потрапить у положення, що відповідає числу t. Таким чином, кожному дійсному числу відповідає одна і тільки одна точка Pt координатної прямої (рис. 276 а, б). Відтак
ми можемо не розрізняти число t і точку Pt .
Так само ми можемо не розрізняти міру кута обертання t і число t. Це дає змогу побудувати відповідність між дійсними числами і точками одиничного кола, користуючись вимірюванням відстані вздовж кола. Для цього на координатній площині розглянемо одиничне коло (тобто коло з радіусом 1) з центром у початку
234 |
Розділ 3. Тригонометричні Функції |
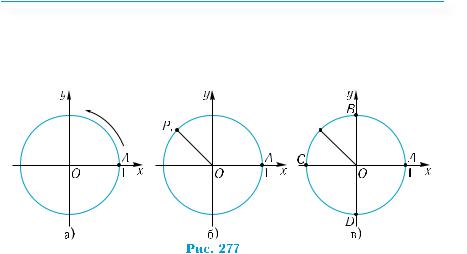
координат (рис. 277, а) — його називають тригонометричним колом. Точку А з координатами (1; 0) називають початком відліку (на колі!). Довільне число t можна зобразити точкою на тригонометричному колі.
Нехай задано число t. Уявімо собі, що деяка точка рухається по
тригонометричному колу. Свій рух вона починає з положення А.
Вважатимемо, що вона рухається проти годинникової стрілки,
тобтовдодатномунапрямі,якщоt >0,ізагодинниковоюстрілкою,
тобто у від’ємному напрямі, якщо t < 0. Якщо t = 0, то точка зна-
ходиться в точці А. Коли пройдена відстань дорівнюватиме |t|, точка потрапить у положення, що відповідає числу t. Позначимо
точку, в яку вона потрапляє, через Pt (рис. 277, б). Зрозуміло, що точка P0 збігається з точкою А.
Таким чином, кожному дійсному числу t на тригонометрично-
му колі відповідає точка Pt . За побудовою, точку Pt одержують з точки А за допомогою повороту її навколо початку координат на t
радіан, оскільки на одиничному колі довжина пройденого шляху
дорівнює модулю радіанної міри кута повороту.
Користуючись наведеною побудовою, неважко вказати точки
тригонометричногокола,яківідповідаютьчислам π, − |
π |
, π, − π, 3π, |
|||
− 3π,2π, −2π, π |
|
2 |
2 |
2 |
|
+ 2π тощо. Справді, шлях довжиною |
|
π вздовж |
|||
2 |
2 |
|
|
|
2 |
кола дорівнює |
1 довжини кола, адже довжина одиничного кола |
||||
|
|
4 |
|
|
|
дорівнює 2π. Точка Pπ |
збігається з точкою В (рис. 277, в). В точку |
||||
Pπ можна потрапити,2 |
якщо пройти в додатному напрямі відстань |
||||
Тригонометричні функції числового аргументу |
235 |
π , тобто довжину одиничного півкола. Точка Pπ збігається з точ- |
||
кою С. У точку P |
π можна потрапити, подолавши у від’ємному на- |
|
− |
2 |
π збігається з |
прямі четверту частину одиничного кола. Точка P |
||
|
− |
2 |
точкою D. Аналогічно, точки P3π , P−π збігатимуться відповідно з
2
точками D, С.
!Продовжуючи ці побудови, дійдемо висновку, що різ-
ним числам може відповідати та сама точка тригонометричного кола.
Ця неоднозначність нагадує таку реальну ситуацію: велотрек
має довжину 350 м, велосипедист знаходиться на відстані 150 м від фінішу. Який шлях він проїхав?
Якщо він тільки розпочав змагання, то він проїхав 350 – 150 =
= 200 м, якщо вже проїхав один круг, то — (200 + 350 1) м = 550 м, два круги — (200 + 350 2) м = 900 м; якщо проїхав п кругів, то
шлях дорівнюватиме (200 + 350 п) м. Тому однозначної відповіді на поставлене запитання дати неможливо.
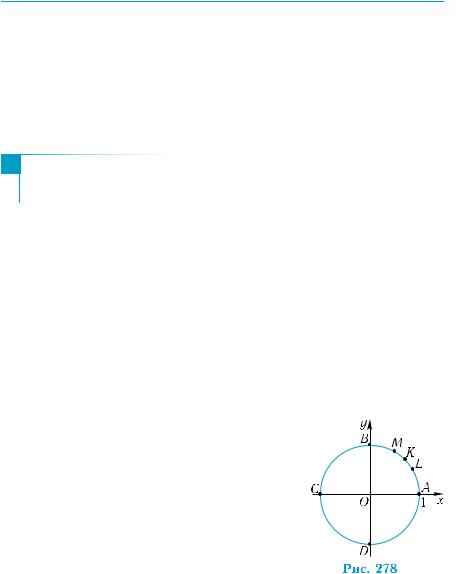
Ïðèê ëàä 3 . Зобразити на тригонометричному колі точки, що відповідають числам 6π; 4π; 3π.
Поділимо дугу АВ, довжина якої дорів-
нює π , навпіл точкою K, на три рівні части- |
|||||
2 |
і M (рис. 278). Тоді довжини |
||||
ни — точками L |
|||||
дугAL,AK,AMвідповіднодорівнюють π; |
π; |
π. |
|||
|
|
|
6 |
4 |
3 |
Відтак, числу π відповідає точка L, числу |
π — |
||||
6 |
|
|
|
4 |
|
точка K, числу π |
— точка М. Ці точки можна |
||||
3 |
|
|
|
|
|
відповідно позначити через Pπ , Pπ , Pπ . |
|
||||
|
6 |
4 |
3 |
|
|
Для точок, побудованих у прикладі 3, неважко вказати прямокутні координати, користуючись співвідношеннями між сторонами і кутами прямокутних трикутників.
236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 3. Тригонометричні Функції |
||||
Ïðèê ëàä |
4. Знайти прямокутні координати точок Pπ , Pπ , Pπ . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
4 |
3 |
Для точки Pπ |
розв’язання зводиться до |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знаходження катетів прямокутного трикут- |
|
|
|||||||||||||||||||||||||
ника, гіпотенуза якого дорівнює 1, а один з |
|
|
|||||||||||||||||||||||||
гострих кутів становить |
|
π |
= 30° (рис. 279). |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
Катет, що лежить навпроти кута 30°, дорів- |
|
|
|||||||||||||||||||||||||
нює 1 ,априлеглийкатетдорівнює |
3 .Отже, |
|
|
||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
2 |
|
|
|
|
||
координати точки P |
|
— |
|
; |
|
. Аналогічно знаходяться коорди- |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нати |
|
1 |
|
; |
|
3 |
|
точки P . Знаходження координат точки P зводить- |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ся до знаходження катетів прямокутного рівнобедреного трикутни- |
|||||||||||||||||||||||||||
ка, гіпотенуза якого дорівнює 1. Його катети дорівнюють |
2 ; |
2 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
Отже, |
P |
|
|
; |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Відповідь. |
|
3 ; 1 |
|
|
2 ; |
|
2 |
|
|
1 ; |
3 |
|
|
|
|||||||||||||
|
; |
|
|
; |
|
. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
2 2 |
|
|
|
2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Користуючись результатом розв’язання прикладу 3, можна знаходити на тригонометричному колі точки, які відповідають числам, вираженим у до-
лях числа π.
Ïðèê ëàä 5 . Зобразити на тригонометричному колі точки, що |
|||||||||||
відповідають числам |
3π |
; − |
5π |
; |
4π |
; |
25π |
. |
|||
|
|
|
|
||||||||
4 |
6 |
3 |
6 |
|
|||||||
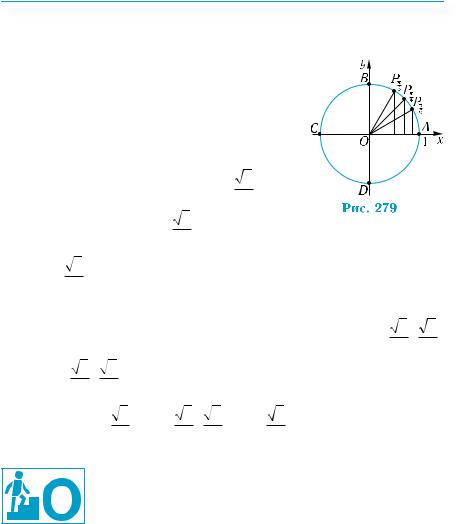
Побудову виконуватимемо, користуючись рис. 278. Відкла- |
|||||||||||
демо тричі від точки А |
дугу |
AK |
(точки K, L, M визначені у при- |
||||||||
кладі 3) у додатному напрямі (її довжина дорівнює 4π ). Одержимо точку Е – середину дуги ВС (рис. 280). Вона і відповідатиме числу
Тригонометричні функції числового аргументу |
237 |
3 π |
= 3π . |
Відклавши дугу AL (її довжина |
|
|
|
|
|||||
|
|
|
|
||||||||
4 |
4 |
π ) від точки А у від’ємному напря- |
|
|
|
|
|||||
дорівнює |
|
|
|
|
|||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
мі 5 разів, матимемо точку F, яка відділяє |
|
|
|
|
|
||||||
третю частину дуги CD. Ця точка і відпові- |
|
|
|
|
|||||||
|
|
|
π |
5π |
. Далі, відклавши |
|
|
|
|
||
дає числу 5 − |
= − |
6 |
|
|
|
|
|||||
|
|
|
6 |
|
|
|
|
|
|
||
дугу АМ (її довжина дорівнює π ) від точки А |
|
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
у додатному напрямі 4 рази, одержимо точку N, яка відділяє дві |
|||||||||||
третини дуги CD. Ця точка і відповідає числу |
4π |
. Нарешті, беру- |
|||||||||
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
чи до уваги, що |
25π |
= 24π + π = 4π + π |
, дійдемо висновку, що числу |
||||||||||||||||
25π |
|
|
6 |
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
відповідає точка L. Якби ми відклали від точки А у додатному |
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напрямі 25 разів дугу AL, то мали б той самий результат. |
|
|
|||||||||||||||||
Координати точок, побудованих у прикладі 4, дозволяють |
|||||||||||||||||||
знаходити координати точок тригонометричного кола, які |
|||||||||||||||||||
відповідають числам, вираженим у долях числа π. |
|
|
|
||||||||||||||||
Приклад |
6. Знайти прямокутні координати точок P5π , P7π , P4π . |
||||||||||||||||||
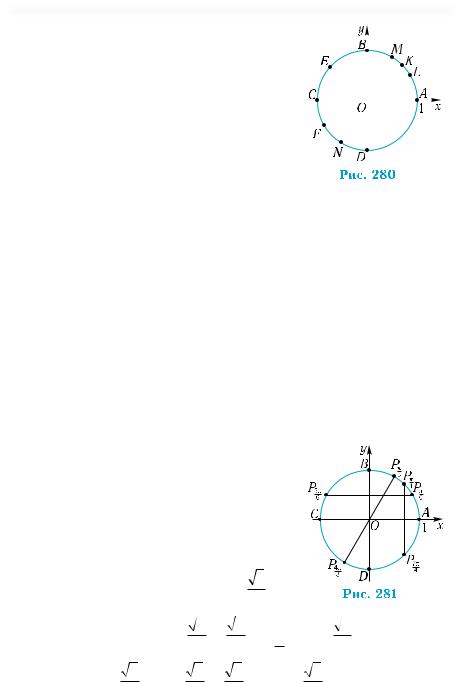
Побудуємо дані точки (рис. 281). Їхні ко- |
|
|
|
6 |
4 |
3 |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
ординати за модулем збігаються відповідно з |
|
|
|
|
|
|
|||||||||||||
координатами точок Pπ , Pπ , Pπ , |
які знайдено |
|
|
|
|
|
|
||||||||||||
|
|
|
|
6 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
у прикладі 4. Слід лише визначити їхні зна- |
|
|
|
|
|
|
|||||||||||||
ки. Точка P5π знаходиться у другій коорди- |
|
|
|
|
|
|
|||||||||||||
натнійчверті6,томуїїабсцисавід’ємна,аорди- |
|
|
|
|
|
|
|||||||||||||
ната |
— |
додатна. |
Відтак, |
P |
|
|
3 |
; 1 |
|
|
|
|
|
|
|
||||
− |
|
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
5π |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||
Аналогічно одержуємо: P |
|
2 ; − |
2 |
|
P |
|
1 ; |
− |
3 |
|
|
|
|||||||
|
, |
− |
. |
|
|
||||||||||||||
|
|
|
|
|
7π |
|
2 |
|
2 |
|
4π |
2 |
|
2 |
|
|
|
||
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|||||
|
|
|
− 3 |
; 1 |
|
|
2 ; − |
2 |
|
|
−1 ; − |
3 |
|
|
|
|
|
||
Відповідь. |
; |
|
|
; |
. |
|
|
|
|
||||||||||
|
|
|
2 |
2 |
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
238 Розділ 3. Тригонометричні Функції
Наближено можна зображати точки тригонометричного кола, які відповідають довільним числам.
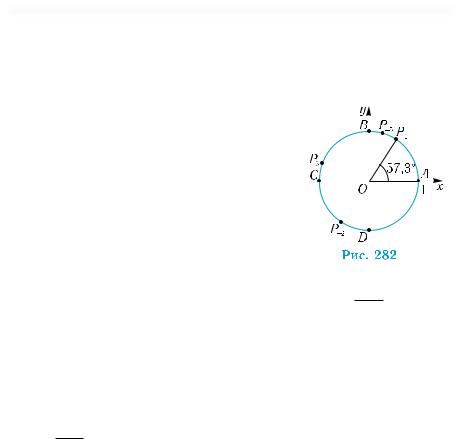
Ïðèê ëàä 7. Зобразити на тригонометричному колі точки, що |
|||||||
відповідають числам 1, – 2, 3, – 5. |
|||||||
|
Числу 1 відповідає точка Р1, яка розмі- |
||||||
щена на дузі АВ ближче до точки В, бо до- |
|
|
|||||
вжина дуги АВ дорівнює π або приблизно |
|
|
|||||
|
2 |
|
|
|
|
|
|
1,5. Щоб уточнити її положення, відкладемо |
|
|
|||||
від точки А у додатному напрямі кут в 1 рад, |
|
|
|
|
|||
|
|
|
|||||
який |
наближено дорівнює |
180° |
≈ 57,3° |
|
|
||
|
|||||||
|
|
π |
|
|
|||
(рис. 282). Його можна побудувати за допомо- |
|
|
|||||
|
|||||||
гою транспортира. Для побудови точки Р–2, |
|||||||
що відповідає числу –2, відкладемо від точки А у від’ємному напря- |
|||||||
мі дугу в 2 рад. Відповідний кут наближено дорівнює 180π ° 2 ≈115°
(див. рис. 282). Ця точка знаходиться на дузі CD ближче до точки D. Аналогічно будується точка Р3, що відповідає числу 3. Вона знаходиться на дузі ВС ближче до точки С (нагадаємо, що точка С відповідає числу π ≈ 3,14). Числу – 5 відповідає та сама точка, що й числу −5 + 2π ≈1,28 . Щоб її побудувати, відкладемо від точки А у
додатному напрямі дугу в 1,28 рад. Відповідний кут наближено дорівнює 180π ° 1,28 ≈ 73° (див. рис. 282). Точка Р–5 знаходиться на
дузі АВ ближче до точки В (нагадаємо, що точка В відповідає чис-
лу π/2 ≈ 1,57).
Відповідність між дійсними числами і точками тригонометричного кола, як відмічалось вище, не є взаємно однозначною. На-
приклад, якщо розглянути числа t |
= |
π |
, t |
= π + 2π , |
t |
= π + 4π , ..., |
||
t = π |
|
0 |
|
2 |
1 |
2 |
2 |
2 |
+ 2πn, …, то положення точки P |
для п = 0, 1, 2, …одне й те |
|||||||
n |
|
|
|
t |
|
|
|
|
|
|
|
|
n |
|
|
|
|
саме2— точка Pπ , тобто точка Pπ відповідає нескінченній кількос- |
||||||||
|
2 |
2 |
|
|
|
|
|
|
ті чисел |
π |
, |
π |
+ 2π, |
π |
+ 4π,… . Це саме положення мають і точки, |
|
2 |
|
2 |
|
2 |
|
Тригонометричні функції числового аргументу |
239 |
які відповідають числам π −2π, |
π −4π, … . Таким чином, точка |
||
|
2 |
2 |
|
P |
відповідає числам π + 2πn , де n Z. |
||
π |
2 |
|
|
2 |
|
||
За прямокутними координатами точки на тригономе- |
|||
! |
|||
тричному колі можна деколи записати числа, яким |
|||
|
|||
|
вони відповідають. |
|
|
Ïðèê ëàä 8 . Знайти на тригонометричному колі точки і записати, яким числам вони відповідають, якщо вони мають: 1) ордина-
ту |
|
2 |
; 2) абсцису − |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
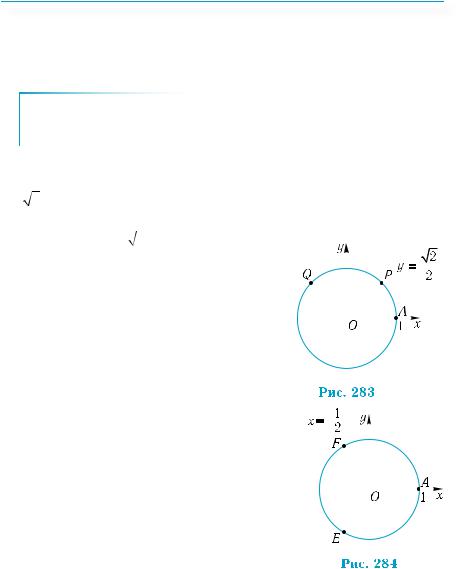
|
|
1) Пряма у = |
|
2 |
перетинає тригоно- |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
метричне коло в точках Р |
і Q (рис. 283). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Точка Р відповідає числу |
π |
(див. прик- |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лад 4), а відтак усім числам |
π |
+ 2πn,n Z . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка Q відповідає числу |
|
3π |
, а відтак |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
усім числам |
3π |
+ 2πn,n Z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
4 |
|
−1 перетинає тригономе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2) Пряма х = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(рис. 284). Точка |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
тричне коло в точках Е і F |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Е відповідає числу |
|
|
|
4π |
(див. приклад 6), а |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
відтак усім числам |
|
4π |
|
+ 2πn,n Z . Точка F |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
відповідає числу |
|
2π |
, а відтак усім числам |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2π |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ 2πn,n Z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
π + 2πn,n Z , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Відповідь. 1) |
|
+ 2πn,n Z ; |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2) |
4π |
+ 2πn,n Z |
, |
2π |
+ 2πn,n Z . |
|
|
|
|||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
240 Розділ 3. Тригонометричні Функції
Контрольні запитання
1°. |
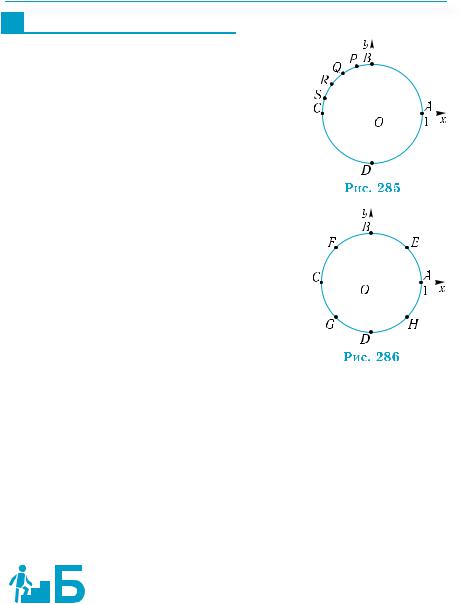
Яким числам відповідають на рис. 285: |
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
а) середини дуг CD і DA; |
|
|
|
|
|
||||||||||||
|
б) точки P, Q, |
R, S , які поділяють дугу |
|
|
|
|
||||||||||||
|
ВС на п’ять рівних частин? |
|
|
|
|
|||||||||||||
2°. |
На |
|
якій |
із дуг |
АВ, |
ВС, CD, DA |
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||||
|
тригонометричного кола (див. рис. 285) |
|
|
|
|
|||||||||||||
|
знаходиться точка, що відповідає числу |
|
|
|
|
|||||||||||||
|
7π |
; |
9π |
; |
2π |
? |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
3°. |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Чому дорівнює довжина дуги AD на |
|
|
|
|
||||||||||||||
|
рис. 285? |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
У якій чверті міститься точка Pt , якщо: |
|
|
|
|
|||||||||||||
|
а) t = |
5π |
; |
|
б) t = − |
5π |
; |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
4 |
|
|
|
|
|
6 |
|
|
|
|
|
|||||
|
в) t = 5,3π ; |
|
г) t = −2,9π? |
|
|
|
|
|||||||||||
5°. |
Яким числам відповідають на тригоно- |
|
|
|
|
|||||||||||||
|
метричному колі (рис. 286) точки: |
|
|
|
|
|||||||||||||
|
а) E, F, |
|
G, |
H, що поділяють відповідно |
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
|
дуги АВ, ВС, CD, DA навпіл; |
|
|
|
|
|||||||||||||
|
б) що поділяють дуги АВ, ВС, CD, DA на три рівні частини? |
|||||||||||||||||
6. |
Знайдіть числа з проміжку [0; 2π ], яким на одиничному колі |
|||||||||||||||||
|
відповідає точка з: |
|
в) ординатою –1; |
|||||||||||||||
|
а) ординатою 1; |
б) ординатою 0; |
||||||||||||||||
|
г) абсцисою 0; |
|
ґ) абсцисою 1; |
д) абсцисою –1. |
||||||||||||||
7. |
Які координати мають точки тригонометричного кола, що від- |
|||||||||||||||||
|
повідають числам: |
|
|
|
|
|
||||||||||||
|
а) 3π ; |
|
|
|
|
б) |
19π |
; |
в) − π ; |
|
|
г) 2π ? |
||||||
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3. Означення тригонометричних функцій |
|||||||||||||
|
|
|
|
|
|
|
Узагальнимо поняття синуса, косинуса, тангенса |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
і котангенса кута на кути обертання чи на довільні |
|||||||||||
|
|
|
|
|
|
|
числа, які ми домовились не розрізняти. |
|||||||||||
|
|
|
|
|
|
|
|
|
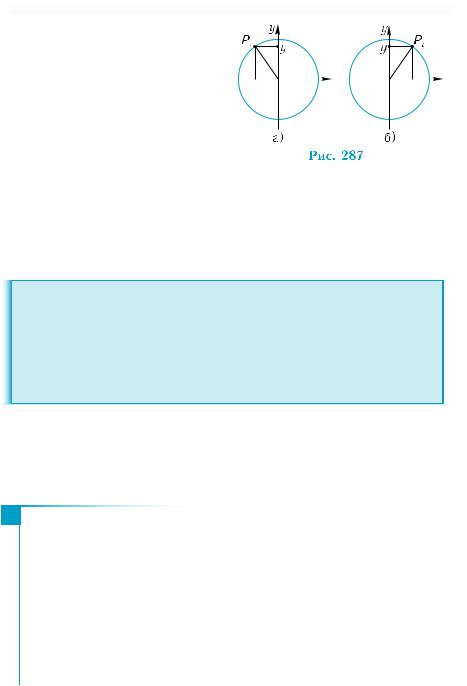
Нехай задано довільне число t, яке визначає точ- |
|||||||||
ку Pt на тригонометричному колі. Позначимо через (х; у) координати точки Pt (рис. 287, а).
Тригонометричні функції числового аргументу |
241 |
Синусом числа t назива-
ється ордината точки Pt. sin t = у.
Косинусом числа t назива- 
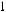

 ється абсциса точки Pt.
ється абсциса точки Pt. 

cos t = х.
Тангенсом числа t назива-
ється відношення синуса числа t до його косинуса.
tg t = cossintt .
Котангенсом числа t називається відношення косинуса числа t до його синуса.
ctg t = cossintt .
Косинус — від латинського complementi sinus: complementus — доповнення, а sinus — западина,
заглиблення; буквально: доповнення заглибини.
Тангенс — від латинського tangens — той, що дотикається, tango — дотикаюсь.
Котангенс — від латинського complementi tangens.
Кожному числу t відповідає єдина точка Pt тригонометричного
кола, а отже, єдині абсциса та ордината цієї точки. Власне, саме тому sin t, cos t, tg t, ctg t є функціями змінної t, яка набуває значень з множини дійсних чисел. Їх називають тригонометрич-
ними функціями.
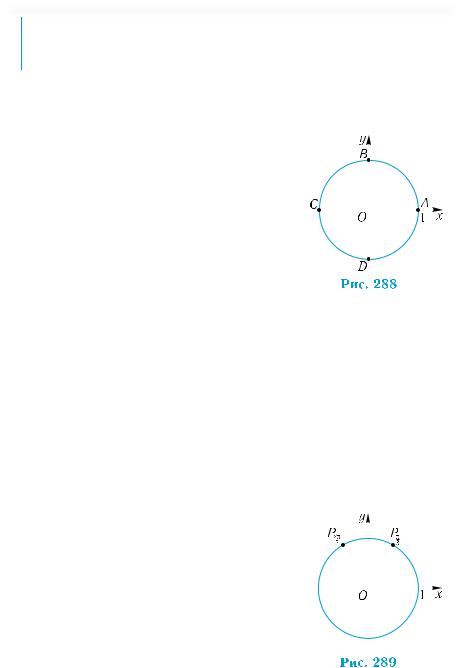
!Для кутів, які розглядаються в геометрії, наведені означення збігаються з означеннями відповідних величин у геометрії. Якщо кут t лежить у першій координатній
чверті, то абсциса і ордината точки Pt є довжинами катетів прямокутного трикутника ОPt Q (рис. 287, б). У цьому
випадку означення тригонометричних функцій є тими самими, якими вони були для гострих кутів прямокутного трикутника. В інших чвертях значення тригонометричних функцій також можуть бути знайдені з прямокутних трикутників, тільки при цьому слід враховувати
16 Математика, 10 кл.
242 |
Розділ 3. Тригонометричні Функції |
знаки координат точки Pt і зв’язок кута t з гострим ку- |
|||||||||||||||||||||||
том трикутника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ïðèê ëàä |
9. Знайти значення тригонометричних функцій чи- |
||||||||||||||||||||||
сел 0; π; π; |
3π |
; 2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для розв’язання задачі потрібно |
|
|
|
|
|
|
|
|
|
||||||||||||||
знайти прямокутні координати точок триго- |
|
|
|
|
|
|
|
|
|
||||||||||||||
нометричного кола, які відповідають зазна- |
|
|
|
|
|
|
|
|
|
||||||||||||||
ченим числам, |
тобто |
точок |
A = P0 = P2π , |
|
|
|
|
|
|
|
|
|
|||||||||||
B = Pπ ,C = Pπ , D = P3π (рис. 288). Враховуючи, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
що радіус тригонометричного кола дорівнює 1, |
|
|
|
|
|
|
|
|
|
||||||||||||||
маємо: Р0(1; 0), Pπ (0;1), Pπ (−1; 0), P3π (0; −1). |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
sin π |
2 |
|
|
|
3π |
|
|
|
|
|||||
Отже, sin 0 = sin 2π = 0, |
=1, sin π = 0, |
sin |
= −1, cos 0 = |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||
=cos2π =1, cosπ = 0, cosπ =–1, |
cos3π = 0, tg0 = sin 0 = 0 = 0 = tgπ = |
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
cos0 |
1 |
|
|
||||||||
= tg2π. tg π |
, tg |
3π |
|
не існують. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
2 |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
π |
|
cos |
= 0 = 0 = ctg 3π; ctg 0, ctg π, ctg 2π не іс- |
|||||||||||||||
Аналогічно, ctg |
= |
2 |
|||||||||||||||||||||
2 |
|
π |
|||||||||||||||||||||
|
|
|
|
|
|
sin |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нують, бо на нуль ділити неможливо. |
|
|
|
|
|
|
|
|
|
||||||||||||||
Ïðèê ëàä |
10 . Знайти значення тригоно- |
|
|
|
|
|
|
|
|
|
|||||||||||||
метричних функцій числа |
|
2π |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Треба спочатку знайти прямокутні ко- |
|
|
|
|
|
|
|
|
|
||||||||||||||
ординати точки P2π . За модулем вони збіга- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ються з відповідними координатами точки |
|
|
|
|
|
|
|
|
|
||||||||||||||
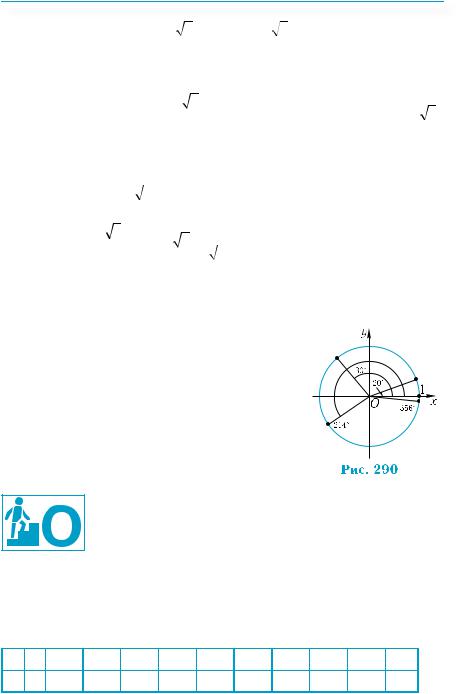
Pπ (рис. 289). Застосовуючи співвідношення |
|
|
|
|
|
|
|
|
|
||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
між сторонами і кутами прямокутного три- |
|
|
|
|
|
|
|
|
|
||||||||||||||
Тригонометричні функції числового аргументу |
|
|
|
|
|
|
|
|
|
243 |
||||||||||||||||||||||||
кутника, маємо, що P |
|
1 ; |
|
3 |
|
|
, P |
|
− |
1 ; |
3 |
|
(див. приклад 4, п. 2). |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
2 |
|
|
2 |
|
|
|
2π |
|
2 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||
Тому,враховуючиозначеннятригонометричнихфункційдовільного |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2π |
|
|
3 |
|
|
|
|
2π |
|
1 |
|
2π |
|
sin |
2π |
|
|
|||||||||
числа, |
одержимо: |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||
sin |
|
3 |
|
= |
|
|
|
|
; |
cos |
3 |
|
= −2 |
; |
tg 3 |
= |
|
|
= − |
3; |
||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
cos |
2π |
|||||||||||||||||||||||||||
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
ctg 2π |
|
cos |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
3 |
= = − |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
sin |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
3 |
; − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Відповідь. |
|
; |
|
− |
|
3; − |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Знаки значень тригонометричних функцій числа t визначаються положенням точки Pt на тригонометричному колі.
Ïðèê ëàä 11. |
Визначити знаки чисел: |
||||
sin 20°; cos 130°; tg 214°; ctg 356°. |
|||||
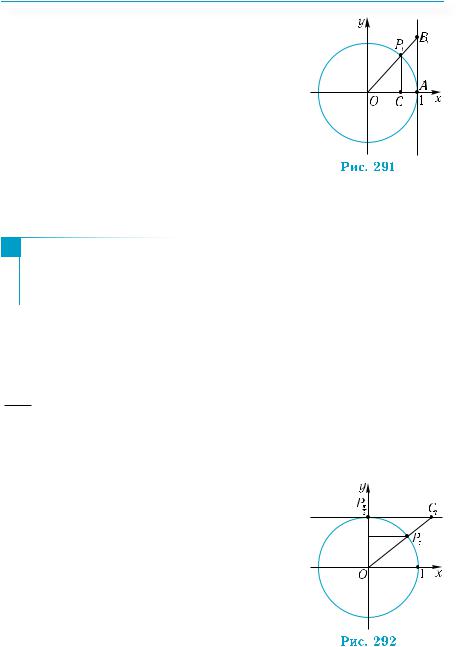
Побудуємо на тригонометричному колі |
|||||
точки, які відповідають кутам обертання на |
|||||
20°; 130°; 214°; 356° (рис. 290). Далі, скорис- |
|||||
тавшись означеннями тригонометричних |
|||||
функцій, матимемо: sin20° > 0, cos130° < 0, |
|||||
tg214° = |
sin 214° |
> 0, ctg356° = |
cos356° |
< 0 . |
|
|
|
||||
|
cos214° |
|
sin356° |
||
При обчисленні значень тригонометричних функцій числа (або ж те саме, що міри кута обертання, заданого в радіанній мірі) за допомогою калькулятора перемикач встановлюють у положення Р (ра-
діан). Це саме роблять при знаходженні значення аргументу за |
||||||||||||
заданим значенням тригонометричної функції. |
|
|
|
|||||||||
Ïðèê ëàä |
12 . Скласти таблицю значень функції h = t + sin t |
|||||||||||
для таких значень t: 0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1. |
|
|||||||||||
|
Щоб виконати завдання, скористаємось калькулятором. |
|
||||||||||
t |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
h |
0 |
0,200 |
0,399 |
0,596 |
0,789 |
0,979 |
1,16 |
1,34 |
1,52 |
1,68 |
1,84 |
|
16*
244 |
Розділ 3. Тригонометричні Функції |
Синус і косинус довільного числа ми визначили геометрично. Натомість тангенс
і котангенс ввели як деякі відношення синуса і косинуса. Проте їх також можна охарактеризувати геометрично.
Пряма, що проходить через точку з координатами (1; 0) перпендикулярно до осі абсцис, називається
лінією тангенсів (рис. 291).
Лінія тангенсів має рівняння х = 1, її можна вважати координатною прямою з напрямом і масштабом осі у і з початком у точці А.
! Кожному числу t ≠ 2π(2n +1), n Z, можна поставити у
відповідність точку Вt на лінії тангенсів, яка є точкою перетину прямої OPt з лінією тангенсів.
Доведемо, що ордината точки Вt дорівнює tg t, якщо точка Рt знаходиться у першій чверті.
З подібності трикутників OPt С і ОВt А маємо: OCPCt = ABOAt , або
sincostt = AB1 t , tgt = ABt .
Цей висновок є правильним і тоді, коли точка Pt міститься
не у першій чверті тригонометричного кола. Пропонуємо переконатись у цьому самостійно.
Пряма, що проходить через точку з координатами (0; 1) перпендикулярно до осі ординат, називається лінією котангенсів (рис. 292).
Лінія котангенсів має рівняння у = 1, її також можна вважати координатною прямою з напрямом і масштабом осі х і з почат-
ком у точці Pπ .
2
Доведіть самостійно, що абсциса точки Ct перетину прямої OPt з лінією котангенсів дорівнює ctg t.
Тригонометричні функції числового аргументу |
245 |
Ïðèê ëàä 13 . Зобразити на тригонометричному колі точки Рt,
якщо: 1) tg t = 2; 2) tgt = –0,5; 3) ctgt = 1,5.
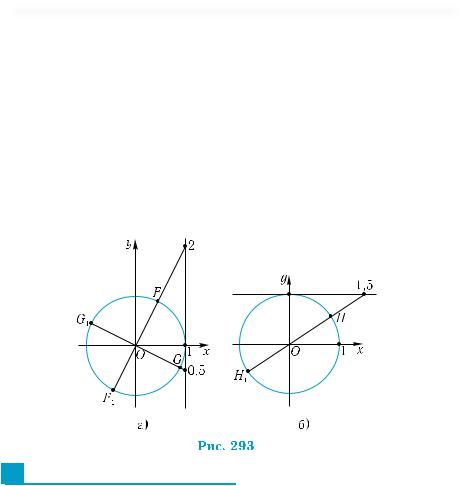
1) Відкладемо на лінії тангенсів у додатному напрямі відрізок, що дорівнює 2 (нагадаємо, що радіус кола дорівнює 1). Через отриману точку і центр тригонометричного кола проведемо пряму. Точки F і F1 перетину цієї прямої з колом і будуть шуканими
(рис. 293, а).
2) У від’ємному напрямі лінії тангенсів відкладемо відрізок завдовжки 0,5. Далі задача розв’язується аналогічно попередній. Точки G і G1 є шуканими (див. рис. 293, а).
3)Відрізокзавдовжки1,5відкладаємоудодатномунапрямілінії котангенсів. Далі задача розв’язується аналогічно попередній. Точки Н і Н1 є шуканими (рис. 293, б).
Контрольні запитання
1°. Дано точку Pt (−0,8; 0,6) на тригонометричному колі. Чому до-
рівнює: а) sint; б) cos t; в) tg t; г) ctg t?
2°. Чиможесинусдеякогочисладорівнювати 78 ; 78 ; − 78 ; − 78 ; 3π; 4π?
3. Скільки чисел t, що задовольняють умову cos t = 1, містяться у проміжку [0; 4π ]?
4. Чи завжди існує на проміжку [0; π ] число, яке задовольняє умову tg t = a, де а — довільне дійсне число?
5. Скільки чисел t, що задовольняють умову sin t = 0,4, містяться у проміжку [0; 2π ]?

246 |
|
|
|
Розділ 3. Тригонометричні Функції |
6. |
Чи правильно, що числам |
π |
і |
5π відповідає та сама точка на |
|
лінії тангенсів? |
4 |
|
4 |
|
|
|
] числа t, для яких sin t = –0,1? |
|
7. |
Чи існують на проміжку [0; π |
|||
Задачі
228°. Запишіть у радіанній мірі значення кутів: |
|
|
|
|
||||||||||
1) |
120°; |
2) 54°; |
3) 210°; |
|
|
4) 165°; |
|
|
||||||
5) |
–330°; |
6) 27°; |
7) 127°12'. |
|
|
|
|
|
||||||
229°. Запишіть у градусній мірі значення кутів: |
|
|
|
|
||||||||||
1) |
π ; |
2) − |
5π |
; 3) 2; |
4) 3π; 5) |
5π |
|
; 6) − |
5π |
; 7) |
3π |
. |
||
|
|
3 |
2 |
|||||||||||
|
3 |
|
6 |
|
4 |
|
|
|
|
|||||
230. Зобразіть на тригонометричному колі кути обертання, раді- |
||||||||||||||
анні міри яких дорівнюють: |
|
|
|
|
|
|||||||||
1°) |
3π |
; |
2°) − π; 3) 2; |
4) –3; |
5) 0,5; |
|
6) –6. |
|||||||
|
|
|||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||
231. Зубчасте колесо має 40 зубців. Виразіть у градусах кут, на який обернеться колесо при повороті на 1 зубець; 15 зубців; 80 зубців; 150 зубців.
232. Серед мір кутів обертання –310°, –220°, –50°, 770° укажіть такі, в яких положення рухомого променя збігається з положенням рухомого променя кута, градусна міра якого до-
рівнює: 1) 50°; 2) 140°.
233. Серед мір кутів обертання −187π, −107π, −137π, −37π, 67π ука-
жіть такі, в яких положення рухомого променя збігається з положенням рухомого променя кута, радіанна міра якого
дорівнює: 1) 7π ; 2) 47π .
234. Знайдіть довжину дуги, якщо відомі її радіанна міра α і радіус R кола, що містить її:
1) α = 3, R = 1 см; 2) α = 23π , R = 3 см; 3) α = 45π , R = 5 м.
235. Колесо за 10 с повернулося на 5π рад. З якою кутовою швидкістю воно обертається?

Тригонометричні функції числового аргументу |
247 |
236.Шків швидкісного електродвигуна робить 90 000 обертів за хвилину. Знайдіть кутову швидкість обертання цього шківа: 1) у град/с; 2) у рад/с.
237.Кліть шахтного підйомника піднімається на 100 м за 40 повних обертів вала підйомника у додатному напрямі. Визначте у радіанах кут повороту вала підйомника, якщо кліть піднялась на 13,75 м; спустилась на 21 м.
238.Точка рухається рівномірно по колу радіуса R = 60 см з кутовою швидкістю ω = 4π рад/с. Знайдіть її лінійну швидкість.
239.Точка рухається рівномірно по колу радіуса R = 30 см з лінійною швидкістю 75 см/с. Знайдіть її кутову швидкість.
240.Яку лінійну швидкість має точка диска, що обертається, коли вона віддалена на 18 см від осі обертання, а кутова
швидкість диска дорівнює 3π рад/с? Якої довжини дугу опише ця точка за 45 с?
241.Зобразіть на тригонометричному колі точки, що відповідають числам:
1°) − |
π; − |
π |
; − |
π |
, 2π, 3π, 5π; |
2) 1,5; 2,3; |
|
|
3) 5π |
; −27π. |
||||||||||
|
6 |
|
4 |
|
3 |
3 |
4 |
6 |
|
|
|
|
|
|
|
|
4 |
|
||
242. Знайдіть прямокутні координати точок: |
|
|
|
|
|
|
||||||||||||||
1°) P |
, P |
|
, P |
|
; |
|
|
|
2°) P |
5π |
, P |
|
, P |
2π |
; |
|
|
|||
|
7π |
3π |
|
5 |
π |
|
|
|
|
− |
|
− |
π |
− |
|
|
|
|||
3) P |
6 |
, P |
4 |
|
3 |
|
; |
|
|
4) P |
6 |
|
|
4 |
|
3 |
|
|
|
|
|
5π |
, P |
|
|
|
, P |
, P |
. |
|
|
|
|||||||||
11π |
− |
−4π |
|
|
|
−π |
|
− |
7π |
|
2π |
|
|
|
|
|||||
6 |
|
4 |
|
|
|
3 |
|
|
|
6 |
|
|
4 |
|
3 |
|
|
|
яку |
|
243. Знайдіть координати точки тригонометричного кола, |
||||||||||||||||||||
одержимо при обертанні точки (1; 0) на кут: |
|
|
|
|
||||||||||||||||
1°) 3π; |
|
|
|
2°) –2π; |
|
3°) 4,5π; |
4) |
π; |
|
|
5) 225°. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
244. Знайдіть кути, на які потрібно повернути точку (1; 0) навколо |
||||||||||||||||||||
початку координат, щоб одержати точку з координатами: |
|
|||||||||||||||||||
1°) |
2 ; |
2 ; |
|
2) − |
2 ; |
2 ; |
3) − |
2 ; − |
|
2 ;4) |
2 ; − |
2 . |
||||||||
2 2 2 2 2 2 2 2
245.Зобразіть на тригонометричному колі точки і запишіть, яким числам вони відповідають, якщо вони мають:
1) ординату − |
3 |
; |
2) абсцису |
2 |
. |
|
2 |
2 |
|||||
|
|
|
|

248 |
Розділ 3. Тригонометричні Функції |
246. Для кожного з наведених значень t |
|
π |
; |
π |
; |
5 |
π; π; |
4 |
π; |
t = |
4 |
2 |
6 |
3 |
|||||
|
|
|
|
|
|
3 |
π; |
11 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pt′ |
стали |
|
2 |
6 |
|
вкажіть таке значення t′ , щоб точки Рt і |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
симетричними відносно: 1) початку координат; 2) осі абсцис; |
|||||||||||||||||||
3) осі ординат; 4*) прямої у = х; 5*) прямої |
у = –х. |
|
|
|
|||||||||||||||
247*. Числа задані формулою: 1) |
t = π |
k ; 2) |
t = π k ; |
3) |
t = π k ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
4) t = |
π (2k +1), де k = 0, ±1, ±2, ±3, ... . Зобразіть на коорди- |
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
натній прямій і на тригонометричному колі точки, які від- |
|||||||||||||||||||
повідають цим числам. Скільки таких точок буде на коорди- |
|||||||||||||||||||
натній прямій і скільки — на тригонометричному колі? |
|||||||||||||||||||
248°. Дано координати точки Рt |
на |
тригонометричному колі. |
|||||||||||||||||
Обчисліть sin t, cos t, tg t, ctg t: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
4 |
|
|
3 |
|
5 |
|
12 |
|
|
3 |
; 1 |
|
|
3 ; |
7 |
|
|
1) |
|
; − |
; |
2) − |
|
|
; |
; |
3) |
− |
; |
4) |
. |
||||||
5 |
13 |
|
|||||||||||||||||
|
4 |
||||||||||||||||||
|
|
|
|
5 |
|
|
13 |
|
2 2 |
|
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
249°. Обчисліть значення тригонометричних функцій чисел:
1) |
|
3π |
; |
|
|
|
2) |
2π |
; |
3) |
5π |
; |
|
4) |
7π . |
|
|
|
||||||||
4 |
|
|
|
|
4 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|||
250°. Визначте знаки тригонометричних функцій sin t, cos t, tg t, |
||||||||||||||||||||||||||
ctg t для t, що дорівнює: |
|
|
|
|
|
|
|
|
||||||||||||||||||
1) |
7π ; |
|
2) |
− |
5π |
; 3) |
|
12π |
; 4) |
−7π ; 5) |
7π ; |
6) |
|
13π |
. |
|||||||||||
|
|
7 |
|
6 |
||||||||||||||||||||||
|
6 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
6 |
|
9 |
|
|
|||||||
251°. Обчисліть: |
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
||||||
1) |
sin π |
+ cos π −2tg2π + ctg |
; |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
3π |
|
|
|
|
π |
|
2 |
|
|
|
5π |
|
|
|
|
|
|||||||
2) |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin − |
2 |
|
− cos |
2 |
|
+ 2tg3π + ctg − |
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
, якщо: |
|||||||
252. Зобразіть на тригонометричному колі точки Р |
||||||||||||||||||||||||||
1)сtg t = 1; 2) сtg t = 2; 3) сtg t = –0,5; 4) tgt = 1,5; 5) tgt = –1.
253.Знайдіть усі числа з проміжку [0; 2π ], які задовольняють умову:
1)sin t = 0; 2) cos t = l; 3) cos t = –1; 4) ctg t = 0; 5) sin t = –1.t
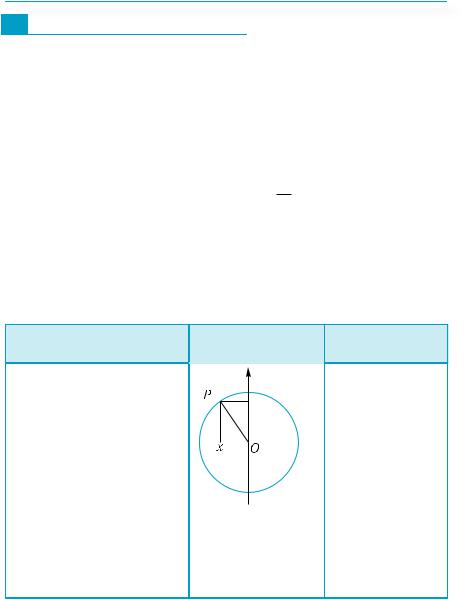
Тригонометричні функції числового аргументу |
249 |
Вправи для повторення
254.Відомо, sin α = а. Знайдіть cos α, tg α, якщо α:
1)гострий кут прямокутного трикутника;
2)тупий кут трикутника.
255.Відношення катетів прямокутного трикутника дорівнює 4:3. Знайдіть синуси і косинуси гострих кутів трикутника.
256.Доведіть, що точка з координатами (cos α; sin α) лежить на колі з радіусом 1 і з центром у початку координат.
257.Із заданої рівності виразіть х через у та у через х:
1)х2 + у2 = 4, якщо x > 0, y > 0; 2) 1 − x12 = y2 , якщо x < 0, y < 0.
258.Дано кути: 30°; 64°; 10°; α; 45° + α; 8π. Знайдіть кути: 1) які доповнюють їх до прямих; 2) суміжні з ними.
Підсумок
Основні поняття
Означення
Синус числа t — ордината точки Pt .
Косинус числа t — абсциса точки Pt .
Тангенс числа t — відношення синуса числа t до його косинуса.
Котангенс числа t — відношення косинуса числа t до його синуса.
Геометрична Застосування інтерпретація
 Тригонометричні функції засто-
Тригонометричні функції засто- 

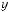 совуються для розв’язування
совуються для розв’язування
 трикутників, до-
трикутників, до-

 слідження обертального руху тощо.
слідження обертального руху тощо.
sin t = у; cos t = х tgt = sincostt ;
ctgt = cost sint
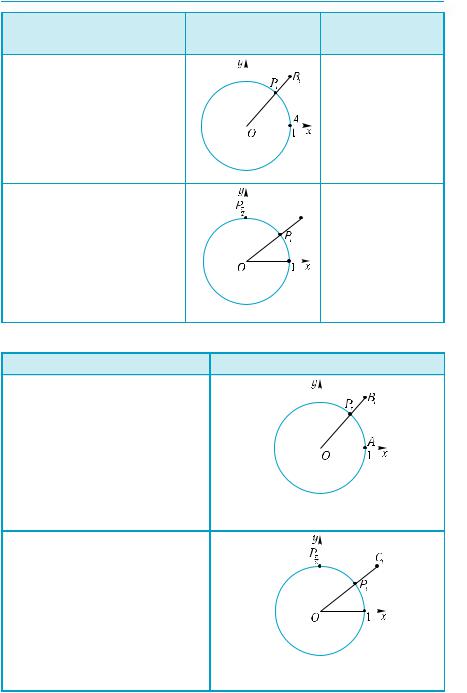
250 |
|
Розділ 3. Тригонометричні Функції |
|||
Означення |
Геометрична |
|
Застосування |
||
інтерпретація |
|
||||
Лінія тангенсів — пряма, |
|
|
|
|
Геометрична |
|
|
|
|||
що проходить через точ- |
|
|
|
|
інтерпретація |
ку (1; 0) перпендикулярно |
|
|
|
|
тангенса |
до осі абсцис, тобто пряма |
|
|
|
|
|
х = 1. |
|
|
|
|
Геометрична |
|
|
|
|
||
Лінія котангенсів — пря- |
|
|
|
|
|
|
|
|
|
||
|
|
|
|||
ма, що проходить через |
|
|
|
|
інтерпретація |
точку (0; 1) перпендику- |
|
|
|
|
котангенса |
лярно до осі ординат, тоб- |
|
|
|
|
|
то пряма у = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Головні твердження
Формулювання |
Геометрична інтерпретація |
||||||||||
Ордината точки Вt |
перетину |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
||||||||||
прямої OPt , яка з’єднує центр |
|
|
|
|
|
|
|
||||
тригонометричного |
кола |
з |
|
|
|
|
|
|
|
||
точкою Pt , з лінією тангенсів |
|
|
|
|
|
|
|
||||
дорівнює tg t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg t = yBt |
|||||||
Абсциса точки Сt |
перетину |
|
|
|
|||||||
|
|||||||||||
прямої OPt , яка з’єднує центр |
|
|
|
||||||||
тригонометричного |
кола |
з |
|
|
|
|
|
|
|
||
точкою Pt , з лінією котанген- |
|
|
|
||||||||
сів дорівнює сtg t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ctg t = xCt |
|||||||
