
- •Звернення до читача
- •Вступ
- •1. Числові множини
- •2. Обчислення і розрахунки
- •3. Функціональні залежності
- •4. Основні властивості функцій
- •5. Корені n-го степеня
- •6. Степеневі функції з раціональними показниками
- •7. Основні поняття й аксіоми стереометрії
- •8. Взаємне розміщення двох прямих у просторі
- •9. Паралельне проектування
- •10. Зображення фігур у стереометрії
- •11. Паралельність прямих і площин
- •12. Паралельність площин
- •13. Тригонометричні функції числового аргументу
- •14. Основні співвідношення між тригонометричними функціями
- •15. Властивості і графіки тригонометричних функцій
- •16. Тригонометричні формули додавання та наслідки з них
- •17. Найпростіші тригонометричні рівняння і нерівності
- •18. Перпендикулярність прямої і площини
- •19. Зв’язок між паралельністю та перпендикулярністю прямих і площин
- •20. Перпендикулярність площин
- •21. Ортогональне проектування
- •22. Перпендикуляр і похила
- •23. Вимірювання відстаней у просторі
- •24. Вимірювання кутів у просторі
- •Відповіді і вказівки до задач

§23. Вимірювання відстаней у просторі
У цьому параграфі розглядається вимірювання відстаней між основними фігурами стереометрії (точкою і площиною, прямою і площиною, площинами).
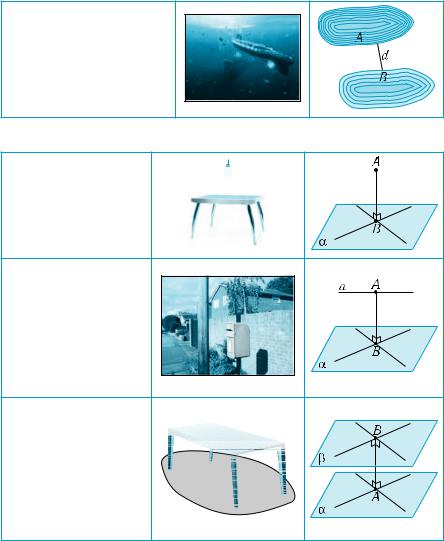
Вимірювання відстаней між різними фізичними 
 об’єктами є одним із найпоширеніших видів матема
об’єктами є одним із найпоширеніших видів матема  тичної діяльності людини. Якщо розмірами об’єктів
тичної діяльності людини. Якщо розмірами об’єктів
можна знехтувати, то йдеться про вимірювання відстаней між точ ками, тобто про визначення довжин відрізків. В інших випадках мо делювання даних об’єктів за допомогою точок при вимірюванні від станей між ними недоцільне чи безглузде, наприклад, коли йдеться про вимірювання відстані між електролампою і столом (рис. 480), якщо першу можна ототожнювати з точкою, то для моделювання стола більш придатна площина чи її частина. Аналогічна ситуація виникає при визначенні відстані між фасадами будівель (рис. 481), що при математичному моделюванні зводиться до визначення від стані між паралельними площинами; при встановленні вертикаль ноїрейкинапевнійвідстанівідстіни(рис.482)(визначеннявідстані між паралельними прямою і площиною) тощо.
Розглянемо питання про вимірювання відстаней між найпро стішими фігурами у просторі. Зміст поняття відстані залишаєть
426 |
Розділ 4. Перпендикулярність прямих і площин |
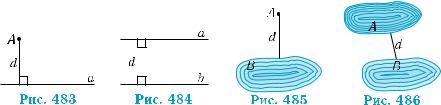
ся таким самим, як і в планіметрії. Наприклад, відстань d від точки A до прямої a — це найкоротша відстань між цією точкою і точками прямої (рис. 483), a відстань між паралельними прямими а і b — це довжина d найкоротшого з відрізків, що сполучає точки цих прямих (рис. 484).
Такий самий зміст має і загальне поняття відстані між фігура- ми. Наприклад, вимірювання відстані d від пункту А до озера В (рис. 485), відстані d між озерами А і В (рис. 486) зводиться до ви- мірювання найкоротшого відрізка, який з’єднує точки цих фігур (точка теж є фігурою).
Узагальнення поняття відстані між фігурами у просторі не ви- кликає труднощів.
Відстанню між фігурами називають довжину най коротшого з відрізків, який сполучає точки даних фігур.
Якщо фігури перетинаються, то будемо вважати, що відстань між ними дорівнює нулю. Це і зрозуміло, бо фігури в цілому «не віддалені» одна від одної. Для фігур, що не мають спільних точок, відстань між ними є однією з мір їхнього взаємного роз- міщення.
Зрозуміло, що задача знаходження відстаней між довіль- ними геометричними фігурами є надто загальною, а тому об- межимося детальним розглядом відстаней між найпростішими фігурами простору — точками, прямими, площинами. Як і в планіметрії, ці відстані реалізуються через довжини відповід- них перпендикулярів. Окрім того, до вказаних ситуацій частогусто зводиться задача про вимірювання відстаней між склад- нішими фігурами.
Теорема 1 (про відстань від точки до площини).
Відстань від точки до площини дорівнює довжині перпендикуляра, проведеного з даної точки до даної площини.
Вимірювання відстаней у просторі |
427 |
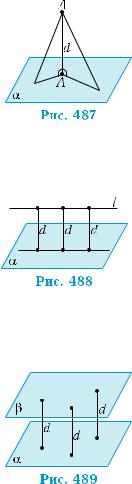
Ця властивість відстані від точки до пло- щини безпосередньо випливає з властивості похилих і перпендикулярів. Справді, пер- пендикуляр, проведений з точки до площи- ни, менший від похилих, проведених з тієї самої точки до точок площини (рис. 487).
Теорема 2 (про відстань між прямою і площиною).
Відстань між прямою і паралельною їй площиною дорівнює довжині перпендикуляра, проведеного з довільної точки прямої до даної площини.
Обґрунтування цієї властивості про від- стань між прямою і площиною спирається на властивості прямої, паралельної площині, і
теорему 1 про відстань від точки до площи- ни. Справді, відстань від кожної точки пря- мої до площини дорівнює довжині перпенди-
куляра, проведеного з даної точки до площини. Для точок прямої, паралельної площині, ці відстані є рівними (рис. 488).
Теорема 3 (про відстань між паралельними площинами).
Відстань між паралельними площинами дорівнює довжині перпендикуляра, проведеного з довільної точки однієї площини до другої площини.
Обґрунтування теореми 3 аналогічне об- ґрунтуванню теореми 2. Відмінність поля- гає лише в тому, що перпендикуляри прово- дяться з усіх точок однієї площини до другої
(рис. 489).
Наведенимивластивостямиширококористуютьсяурізнихсфе- рах діяльності людини, у побуті. Наприклад, за їхньою допомогою визначають відстані від літака до поверхні землі, від світильника до підлоги, від дроту лінії електропередач до поверхні землі, між стелею і підлогою тощо.
Приклад 1. Площини правильного трикутника ABS і квадра- та ABCD зі стороною a — перпендикулярні, точки L, K, M є серед- инами відповідно сторін DC, AB, AS. Знайти відстань:
1) від точки А до прямої ВS;
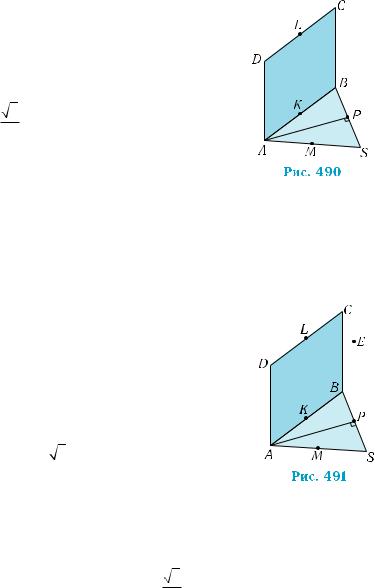
428 |
Розділ 4. Перпендикулярність прямих і площин |
2)від точки А до площини SBC;
3)від прямої AD до площини SBC;
4)між площинами MKL і SBC.
1)Відстань від точки А до дорівнює довжині перпендикуляра ного з точки А до прямої ВS у площині
Оскільки трикутник ABS — правильний таким перпендикуляром буде медіана цього трикутника (рис. 490). Її довжина прямої ВS, проведе ABS., тоАР
дорівнює 23 a.
2) Відстань від точки А до площини SBC дорівнює, за властивістю відстані від точки до площини (теорема 1), довжині перпендикуля-
ра, проведеного з точки А до площини SBC. Цим перпендикуля- ром буде відрізок АР, де Р — середина сторони SB (див. рис. 490). Справді, відрізок АР перпендикулярний до сторони SB трикутни- ка ABS, бо він є медіаною правильного трикутника. Пряма ВС перпендикулярна до площини ABS, бо вона лежить в одній з пер-
пендикулярних площин і перпендикулярна до лінії їхнього пере- |
|||||
тину. Проведемо через точку Р пряму РЕ, па- |
|||||
ралельну прямій |
ВС (рис. 491). Вона лежить у |
||||
площині SBC (чому?) і перпендикулярна до |
|||||
площини ABS, за теоремою про дві паралельні |
|
|
|||
|
|||||
прямі, одна з яких перпендикулярна до пло- |
|
|
|||
щини (теорема 1 § 19): ВС || РЕ, ВС ABS. Тому |
|
|
|||
РЕ ABS. За означенням, РЕ AР. За ознакою |
|
|
|||
перпендикулярності прямої і площини (теоре- |
|
|
|||
ма 1 § 18), АР SВС. Довжина перпендикуля- |
|
|
|||
ра АР дорівнює |
|
3 |
a. Це і є шукана відстань |
||
|
2 |
||||
|
|
|
|
|
|
від точки А до площини SBC. |
|||||
3) Пряма AD |
і площина SBC — паралельні, за ознакою |
||||
паралельності прямої і площини (теорема 1 § 11): AD || ВС. Тому шукана відстань, за властивістю відстані між прямою і площиною (теорема 2), дорівнює відстані від точки А до площини SBC і, за
попереднім завданням, дорівнює 23 a.
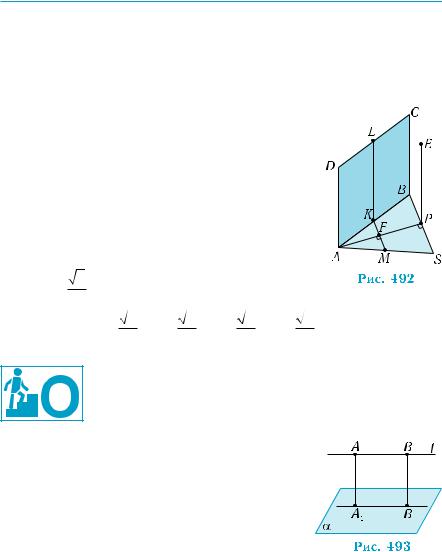
Вимірювання відстаней у просторі |
|
|
429 |
||
4) Площини MKL і SBC — паралельні, за ознакою паралель- |
|||||
ності площин (теорема 1, §12): KМ || BC (KМ — середня лінія три- |
|||||
кутника ABS), KL || BC (KL — відрізок, що з’єднує середини пара- |
|||||
лельних сторін квадрата |
ABСD), тому MKL || SBC. Отже, шукана |
||||
відстань, за властивістю відстані між паралельними площинами |
|||||
(теорема 3), дорівнює довжині перпендикуля- |
|||||
ра, проведеного з довільної точки площини |
|||||
MKL до площини SBC. Візьмемо точку перети- |
|||||
ну F відрізків MK і АР (рис. 492). Оскільки АР є |
|||||
перпендикуляром до площини |
SBC (див. за- |
||||
вдання 2), то FР |
— перпендикуляр до цієї пло- |
||||
щини. Його довжина дорівнює |
1 AP , бо серед- |
||||
|
|
|
2 |
|
|
ня лінія трикутника поділяє медіану, яку вона |
|||||
перетинає, навпіл (чому?). Шукана відстань |
|||||
3 |
|
|
|
|
|
дорівнює 4 a. ■ |
3 a; 2) |
3 a; |
|
3 a; 4) |
3 a. |
Відповідь. 1) |
3) |
||||
|
2 |
2 |
|
2 |
4 |
Розглянемо детальніше доведення властивостей відстаней у просторі. Оскільки теорема 1 є прямим наслідком властивостей похилих і перпендикуля-
рів, розглянемо доведення теореми 2. Нехай маємо пряму l і паралельну до неї
площину α (рис. 493). Оскільки відстань між прямою l і площиною α — це довжина найко-
ротшого відрізка, що сполучає їхні точки, то довжина похилої, яка сполучає точки прямої
і площини, не може бути шуканою відстанню. Доведемо, що довжини всіх перпендикулярів,
проведених із точок прямої l до площини α,
рівні між собою. А тому відстань між прямою і площиною дорів- нює довжині кожного з таких перпендикулярів.
Проведемо з двох точок А і В прямої l перпендикуляри АА1 і ВВ1 до площини α. Оскільки прямі, що перпендикулярні до однієї площини, паралельні між собою (теорема 2 § 19), то через прямі АА1 і ВВ1 можна провести площину, яка містить l. Пряма А1В1 є лі- нією пеpeтину цієї площини з площиною α (чому?). Однак у цьому
430 |
Розділ 4. Перпендикулярність прямих і площин |
випадку АВ || |
А1В1, тобто чотирикутник АА1В1В є паралелограмом |
(навіть прямокутником). Звідси AA1 = BB1. ■
Доведення теореми 3 аналогічне доведенню попередньої тео- реми.
Як і в теоремі 2, похила, що з’єднує дві точки паралельних площин, не може визначати відстань між ними. А всі перпендику- ляри, проведені з точок однієї з площин до другої, паралельні, за теоремою про паралельність прямих, перпендикулярних до пло- щини (теорема 2 § 19). До речі, вони одночасно перпендикуляр- ні до обох площин, за теоремою про паралельні площини, одна з яких перпендикулярна до прямої (теорема 3 § 19).
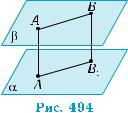
Нехай α і β — паралельні площини, а АА1 і ВВ1 — два довільні перпендикуляри, що
з’єднують точки цих площин (рис. 494). Вони паралельні, а тому рівні, за теоремою про відрізки паралельних прямих між паралель-
ними площинами (теорема 4 § 12). Можна і безпосередньо довести рівність цих відрізків, розглянувши чотирикутник АА1В1В, як це було зроблено при доведенні теореми 2. ■
За допомогою поняття відстані можна характеризувати паралель- ність прямої і площини, паралельність площин. При цьому справджу- ютьсянаступнітвердження,якієоберненимидотеорем2і3.
Теорема 4 (ознака паралельності прямої і площини).
Якщо всі точки прямої лежать на однаковій, відмінній від нуля, відстані від площини, то пряма і площина — паралельні.
Теорема 5 (ознака паралельності площин).
Якщо всі точки однієї площини лежать на однаковій, відмінній від нуля, відстані від другої площини, то ці площини — паралельні.
Справді, при виконанні умов цих тверджень відповідні фігури не можуть мати спільних точок, інакше б відстань між ними до- рівнювала нулю.
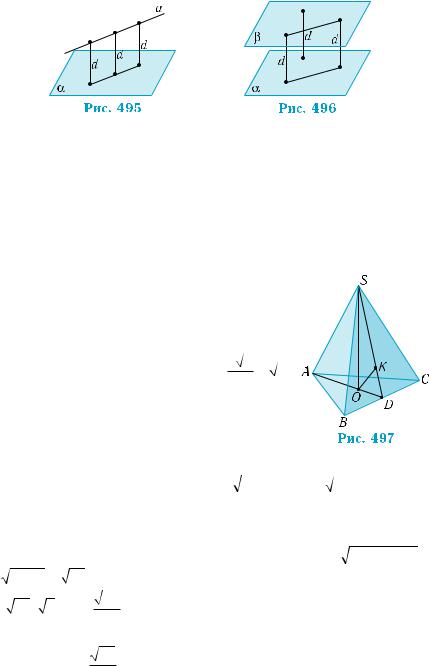
Твердження будуть правильними, якщо умови виконуються не для всіх точок, а для кількох. У першому твердженні досить при- пустити,щоумовавиконуєтьсядлядвохточокпрямої,удругому—
Вимірювання відстаней у просторі |
431 |
для трьох точок, які не лежать на одній прямій (рис. 495, 496). Спробуйте довести це самостійно. Наведені твердження широко використовуються у практиці як ознаки паралельності прямої і площини, двох площин. Так, паралельність поверхні стола до під- логи забезпечується однаковою довжиною його ніжок.
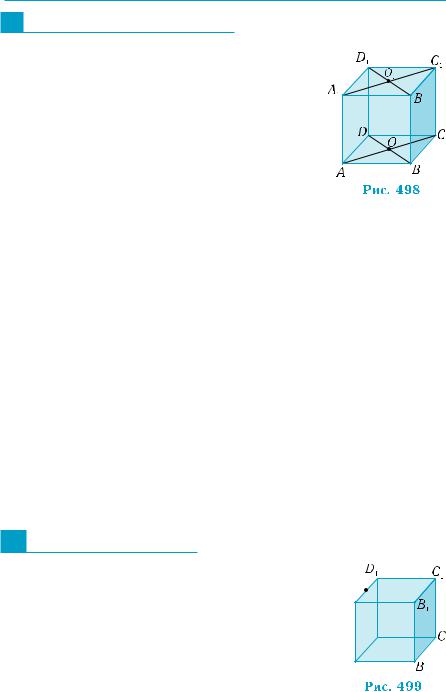
Приклад 2. У тетраедрі SABC основа АВС — рівносторонній трикутник зі стороною 6 см, бічні грані SAB, SAC, SBC — рівнобе- дрені трикутники з бічним ребром 5 см. Знайти відстань від цен- тра О основи до площини бічної грані.
Відстань від точки О до площини SBC дорівнює довжині перпендикуляра ОK із точки О на площину SВС (рис. 497). Точка О лежить на перетині медіан (і висот!) трикут-
ника АВС, причому OD = 1 AD = |
6 |
3 = 3 . |
|
|||
|
|
|
3 |
3 2 |
|
|
Оскільки в трикутнику SBC медіана SD та- |
|
|||||
кож є висотою, то SD BC, тому BC ODC і |
|
|||||
SBC ODC. Отже, перпендикуляр із точки О |
|
|||||
на площину ВSC |
збігається з перпендикуля- |
|
||||
ром ОK із точки О |
на пряму SD, яка є лінією перетину площин SAD |
|||||
і SBC. За теоремою Піфагора, SD = |
SB2 − BD2 = 52 −32 |
= 4 (см). |
||||
Оскількиортогональніпроекціїбічнихребернаоснову—однакові, |
||||||
то |
S ортогонально проектується |
|
в центр описаної |
навколо |
||
трикутника АВС |
кола, тобто в точку О. Тому трикутник |
SOD — |
||||
прямокутний. За теоремою Піфагора, маємо: SO = SD2 −OD2 = |
||||||
= |
16 −3 = 13 |
(см). Неважко побачити, що OK = (SO OD) : SD = |
||||
= ( |
13 3) : 4 = |
39 (см). Зрозуміло |
, з огляду на симетрію, що |
|||
|
|
4 |
|
|
|
|
відстані від точки |
О до інших бічних граней такі самі. ■ |
|
||||
|
Відповідь. |
39 см. |
|
|
|
|
|
|
4 |
|
|
|
|
432 |
Розділ 4. Перпендикулярність прямих і площин |
99 |
Контрольні запитання |
1. |
На рис. 498 зображено куб ABCDA1B1C1D1; |
|
точки О, О1 — центри граней ABCD і |
|
A1B1C1D1. |
|
1) Яка з точок A1, O1, В1 лежить ближче до |
|
нижньої основи куба? |
|
2) Які з ребер куба найбільш віддалені від |
|
площини АА1В1В? |
|
3)Яка з відстаней більша: від прямої АО1 до |
|
площини DСC1 чи від прямої AD1 до площи- |
|
ни BDC1? |
|
4) Чому дорівнює відстань між площинами ADD1 і BCC1? |
2. |
Нехай пряма а паралельна площині α. Чи можуть точки пря- |
|
мої а знаходитись на різних відстанях від точок площини α? |
3. |
Чи правильно, що коли відстань від прямої до площини від- |
|
мінна від нуля, то пряма і площина — паралельні? |
4. |
Відомо, що відрізок AB віддалений від площини α на 3 см. Чи |
|
означає це, що пряма AB віддалена від площини α на 3 см? |
5. |
Чи правильно, що дві площини збігаються, якщо відстань між |
|
ними дорівнює нулю? |
6. |
Чи правильно, що відстань від відрізка до площини дорівнює |
|
відстані від одного з його кінців до цієї площини? |
7. |
Усі сторони трикутника АВС знаходяться на відстані 3 від |
|
площини α. Чи паралельні площини АВС і площина α? |
8. |
Яку фігуру утворюють точки, рівновіддалені від даної пло- |
|
щини? |
9. |
Якпотрібнозакріплюватидрітнастовпах,щобзабезпечитийого |
|
паралельність до поверхні землі? |
10. |
Як виміряти висоту дерева, не піднімаючись до його верхівки? |
Графічні вправи
1.На рис. 499 зображено куб ABCDA1B1C1D1 з ребром а, точки М, М1 — середини ребер AD1, 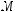 A1D1 відповідно. Знайдіть відстань:
A1D1 відповідно. Знайдіть відстань: 
1)від точки A1 до прямої AB;
2)від точки D1 до прямої AB; 
3)від точки A1 до площини BCC1B1; 
4)від точки A1 до площини AB1C1D; 
Вимірювання відстаней у просторі |
433 |
5)від точки М1 до площини AB1C1D;
6)від прямої A1D1 до площини AB1C1D;
7)від прямої AD1 до площини AB1C1D;
8)між площинами AA1D1 і BB1C1.
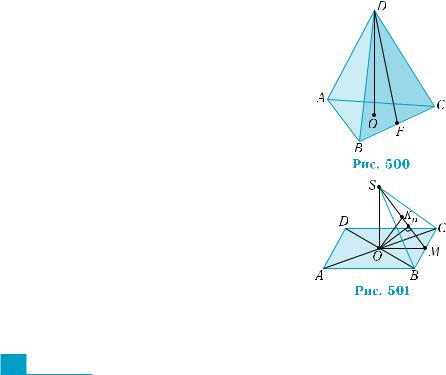
2.Нарис.500зображеноправильнийтетра- едр ABCD, F — середина ВС, О — центр грані АВС. Довжина якого відрізка до- рівнює відстані:
1)від точки D до площини АВС;
2)від точки D до прямої ВС;
3)від точки С до площини АОВ?
3.З центра О квадрата ABCD (рис. 501) проведено перпендикуляр OS до пло- щини квадрата. Точка М — середина
,Р — основа висоти трикутника OMS,
—його медіана. Довжині якого від- різка дорівнює відстань:
1)від точки O до площини BCS;
2)від точки S до площини АВС;
3)від точки С до площини BDS?ВСOK
Задачі
462. Точка D знаходиться на відстані 8 см від вершин рівносторон- нього трикутника ABC зі стороною 4 см. Знайдіть відстань: 1°) від точки B до площини DOC, де O — центр трикутника
ABC;
2°) від точки D до площини ABC;
3) від площини, що проходить через середини відрізків DA, DB, DC, до площини трикутника ABC.
463. Нехай точка O є серединою катета AC прямокутного рівно- бедреного трикутника з гіпотенузою AB = 4 см; OP — пер- пендикуляр до площини трикутника завдовжки 2 см. Знай діть відстань:
1°) від точки B до площини AOP;
2°) від площини, що проходить через середини сторін CB і AB паралельно OP, до площини CPA;
3) від точки O до площини PAB.
464°. З точки K, яка є серединою гіпотенузи АВ рівнобедреного прямокутного трикутника АВС, з катетами завдовжки 8 см,
28 Математика, 10 кл.
434 |
Розділ 4. Перпендикулярність прямих і площин |
проведено перпендикуляр KS до площини трикутника. До- вжина KS становить 6 см. Знайдіть відстань:
1) від точки С до площини AKS;
2) від точки А до площини KCS;
3) від точки S до прямої ВС.
465. Дано куб ABCDA1B1C1D1 з ребром а. Знайдіть відстань: 1°) від точки А1 до площини BDD1;
2°) від прямої В1D1 до площини АВС; 3°) між протилежними гранями куба; 4°) від точки А1 до прямої BD;
5) між прямими AD1 i CC1;
6*) від точки A1 до площини AB1D1;
7*) між площинами CD1B1 і DA1B.
466. Точка М лежить на відстані b від усіх вершин квадрата ABCD зі стороною а і центром в точці О. Знайдіть відстань: 1°) від точки М до площини АВС;
2°) від точки А до площини ВМD;
3) від точки О до площини МСD, якщо b = 23 a ;
4) від точки M до прямої CD;
5) між прямими ОМ і АD.
467. Кінці відрізка віддалені від деякої площини на 1 см і 4 см. Знайдіть відстань від середини відрізка до площини.
468. Катети прямокутного трикутника дорівнюють 16 см і 12 см. На якій відстані від площини трикутника лежить точка,
віддалена від кожної вершини трикутника на 10 2 см? 469. Сторона рівностороннього трикутника дорівнює 6 см. На
якій відстані від площини трикутника розміщена точка, яка віддалена на 9 см від:
1) сторін трикутника; 2*) кожної з прямих, що містять сторони трикутника?
470°. Якщо з двох точок, які знаходяться на різних відстанях від площини, провести рівні похилі, то на цій площині більшою буде проекція тієї похилої, що проведена з ближчої до пло- щини точки. Доведіть це.
471. Якщо з точки А, що знаходиться поза площиною α, опусти- ти перпендикуляр на цю площину, а з його основи провести

Вимірювання відстаней у просторі |
435 |
перпендикуляр до прямої ВС, яка лежить в площині α, то площина, що проходить через ці перпендикуляри, буде пер- пендикулярною до прямої ВС. Доведіть це.
472*. Плиту прямокутної форми підняли краном так, що три її вер- шинивіддаленівідповерхніземлі,відповідно,на2м,3мі4м. На якій відстані від землі перебуває четверта вершина?
473*. Точка А віддалена від сторін кута, що дорівнює 60°, на 20 см і 7 см, а від його вершини — на 25 см. Знайдіть відстань від точки А до площини кута.
474*. Точка, що лежить поза площиною прямого кута, знаходить- ся на відстані 4 см від кожної з його сторін. Знайдіть від- стань від точки до вершини кута, якщо точка віддалена від
7см.
475.Площини квадрата ABCD і рівностороннього трикутника ABМ — взаємно перпендикулярні, AB = а. Побудуйте спіль- ний перпендикуляр прямої AC і медіани МО трикутника і визначте довжину цього перпендикуляра.
476.Нехай AB — спільний перпендикуляр до мимобіжних пря- мих а і b. Точки А і С лежать на прямій а, точки B і D — на прямій b; AC = BD. Доведіть, що ACD = BDС.
Вправи для повторення
477.В одній півплощині, обмеженій прямою АВ, побудовано кути: ВАС = 38°, CАD = 68°, DАE = 85°, EАK = 99°.
Визначте KАC.
478.Один із суміжних кутів утричі більший від різниці між ними. Визначте їхню градусну міру.
479.Спостерігач, що знаходиться на березі озера на висоті h над рівнем води, бачить хмарку під кутом α, а її відображен- ня — під кутом β до горизонту. Знайдіть висоту хмарки над поверхнею озера при α = 53°27′, β = 55°42′, h = 76,8 м.
28*
436 |
Розділ 4. Перпендикулярність прямих і площин |
Підсумок
Головне означення
Відстанню між довіль- ними фігурами назива-
ють довжину найкорот- шого з відрізків, який сполучає точки даних фігур.
Властивості відстаней
Відстань від точки до площини дорівнює довжині перпенди- куляра, проведеного
з даної точки до да- ної площини.
Відстаньміжпрямою і паралельною до неї
площиною дорівнює довжині перпенди- куляра, проведено-
го з довільної точки прямої до даної пло- щини.
Відстань між пара- лельними площина- ми дорівнює довжи- ні перпендикуляра, проведеного з до- вільної точки однієї площини до другої площини.
