В заключение отметим, что комбинационную схему всегда можно избавить от ошибочного поведения при следующих условиях:

1)ограничить изменения на входах изменениями только одного сигнала в каждый момент времени;

2)обеспечить построение схемы, свободной от состязаний;

3)обеспечить достаточное время ожидания между изменениями на входе с тем, чтобы все элементы схемы пришли в устойчивое состояние.

Условия (1) и (3) налагают ограничения на внешнюю среду для того, чтобы получить желаемое поведение схемы. Условие (2) налагает ограничение на структуру схемы.

СОСТЯЗАНИЯ СИГНАЛОВ В ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМАХ

Последовательностные схемы

Цифровую схему называют последовательностной, если состояния ее выходов зависят не только от входных сигналов в данный момент времени, но и от сигналов, поданных ранее.

Принципиальная разница между комбинационными и последовательностными схемами заключается в том, что для последних рассматривают временные последовательности входных и выходных сигналов.

Однако вместо явно заданной переменной времени обычно используют понятие состояния последовательностной схемы, считая, что ее выходной сигнал в любой момент времени t зависит от входного воздействия и состояния схемы также в момент времени t. Состояние хранит информацию о прошлых входных воздействиях, подававшихся на последовательностную схему. Эта информация запоминается в последовательностной схеме в виде внутреннего сигнала или совокупности внутренних сигналов. Например, состояние счетчика указывает на количество поступивших считаемых сигналов.

153

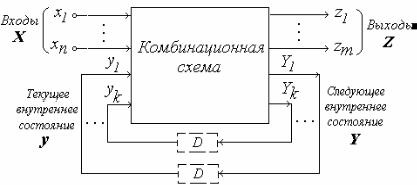
Для того чтобы связать поведение последовательностной схемы с понятием состояния схемы, рассмотрим структурную модель асинхронной последовательностной схемы (рис. 6.8). Она состоит из комбинационной схемы и обратных связей (ОС), каждая из которых может содержать элемент задержки. Комбинационная схема имеет n + k входов, первые из которых являются входами всей схемы, а вторые — входами ОС.

Рис. 6.8. Структурная модель асинхронной последовательностной схемы

Переменные y1, y2, . . . , yk, обозначающие входы ОС, называют

внутренними переменными. Состояние входов ОС является внут-

ренним состоянием последовательностной схемы в данный момент

времени. Совокупность переменных x1, x2, . . . , xn, y1, y2, . . . , yk описывает полное состояние последовательностной схемы в дан-

ный момент времени.

Выходами комбинационной схемы являются выходы всей схе-

мы z1, z2, . . . , zm и выходы ОС Y1, Y2, . . . , Yk.

Если при неизменном состоянии входов X сигналы на входе и выходе элементов задержки одинаковы, т.е. y = Y, то асинхронная последовательностная схема находится в устойчивом состоянии. При изменении состояния входов X может измениться один или несколько выходов Y комбинационной схемы. Таким образом, значение выхода элемента задержки будет отличаться от значения его входов, т.е. y ≠ Y . В этом случае схема находится в неустойчивом

состоянии. Через промежуток, равный времени задержки, значения

154

y изменятся и будут равны значениям Y. Если полученное полное состояние устойчиво, то сигналы на выходах Y комбинационной схемы больше изменяться не будут. Если же полное состояние неустойчиво, то выходы Y будут изменяться до тех пор, пока не наступит устойчивое состояние. Отсюда ясно, что переменные Y описывают внутреннее состояние асинхронной схемы в следующий момент времени.

Условия надежного функционирования асинхронной схемы

Рассматривая структурную модель асинхронной схемы (см. рис. 6.8), можно определить требования, которые будут гарантировать надежную работу проектируемой схемы.

Поскольку комбинационную часть последовательностной схемы строят из логических элементов, обладающих задержками, то необходимо, чтобы она не содержала условий для статических и динамических состязаний сигналов. Комбинационную схему можно спроектировать свободной от состязаний только в случае, если переходы между входными состояниями ограничены изменением одной входной переменной xi. При этом частота изменений сигналов на входах комбинационной схемы должна быть такова, чтобы схема успела полностью отреагировать на предыдущее входное воздействие. Ограничив смену входного состояния изменением только одной переменной xi, также следует ограничить переход схемы из одного состояния в другое изменением одной внутренней переменной yj.

Критические состязания

Если после изменения входного состояния одновременно изменяют свое значение более одной внутренней переменной, то говорят, что в схеме существуют состязания. Если получаемое при этом конечное внутреннее состояние является не единственным, а зависит от порядка изменения внутренних переменных, то состязания называют критическими.

Критическое состязание — это состязание между сигналами обратной связи, которое в зависимости от порядка переключения данных сигналов приводит схему в различное устойчивое состояние.

155

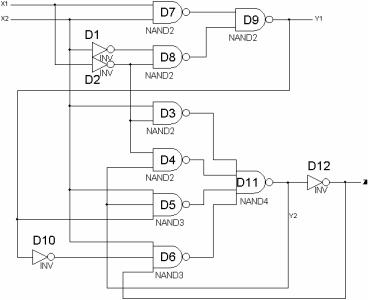
Критические состязания должны быть исключены, так как они в зависимости от распределения задержек в комбинационной схеме могут привести к ошибочным переключениям.

Рассмотрим асинхронную схему, изображенную на рис. 6.9. Допустим, что схема находится в устойчивом состоянии при x1 = 0 , x2 = 1, y1 = 0, y2 = 1, z = 0.

Рис. 6.9. Асинхронная схема и ее таблица переходов

156

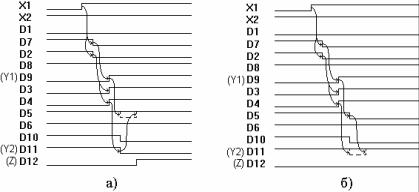
Рис. 6.10. Временные диаграммы, иллюстрирующие критическое состязание сигналов

Изменим x1 с 0 на 1. В соответствии с таблицей переходов выход схемы z должен переключиться с 0 на 1.

Входной сигнал вызовет почти одновременное переключение двух внутренних сигналов Y1 и Y2 (рис. 6.10(а)). Эти изменения с небольшим интервалом поступят по обратной связи на вход элемента D5 (см. рис. 6.9). Первым поступит изменение 0/1 сигнала Y1 и вызовет переключение элемента D5 в 0. Затем придет изменение 1/0 сигнала Y2 . Если это изменение поступит через время, меньшее чем время задержки элемента D5, то оно отменит запланированное ранее переключение элемента D5 в 0. Эта отмена показана пунктирной линией на временной диаграмме элемента D5 (см. рис. 6.10(а)). Выход схемы z переключится с 0 на 1.

При более позднем поступлении сигнала Y2 элемент D5 успеет переключиться в 0 и тогда своим новым значением отменит запланированное переключение элемента D11 (сигнала Y2). Эта ситуация показана на рис. 6.10(б). Выход схемы z останется в прежнем состоянии.

Таким образом, для этой схемы достаточно небольшого отклонения в моментах срабатывания элементов, чтобы была нарушена правильность перехода из-за критического состязания сигналов.

157