Функциональные и логические состязания сигналов

Состязания в комбинационной схеме различают также в зависимости от количества входов, которые изменились при переходе от одного входного состояния в другое. Состязания, обусловленные одновременным изменением нескольких входных сигналов, отличаются от состязаний, возникающих при изменении оного входного сигнала, тем, что они не всегда могут быть устранены преобразованием выражения для функции. Если состязание возникает при одновременном изменении М входных сигналов, то в этом случае его называют М-состязанием.

Определение 3. Комбинационная схема содержит статическое М-состязание при одновременном изменении М входных сигналов, если:

•выходной сигнал перед изменением равен выходному сигналу после изменения входного состояния;

•во время переключения входных сигналов на выходе может появиться ложный импульс.

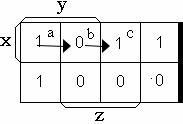
Существуют два различных типа статических М-состязаний. Первый тип, называемый функциональным состязанием, проиллюстрируем с помощью диаграммы Вейча, изображенной на рис. 6.6.

Допустим, входное состояние изменяется от Х = 1, Y = 1, Z = 0 (состояние "а") к X = 1, Y = 0, Z = 1 (состояние "с"). Если изменение переменной Z произойдет быстрее, чем изменение переменной Y, то временно наступит промежуточное состояние "b" (X = Y = Z = = 1). Так как на данном наборе функция равна 0 (см. рис. 6.6), то на выходе схемы может появиться нулевой ложный импульс.

Рис. 6.6. Иллюстрация функционального состязания

149

Пусть переход из состояния входов А к входному состоянию В осуществляется изменением m переменных, т.е.

A = (a1 , ..., am , am+1 ,..., an ),

B = (a1 ,..., am , am+1 ,..., an ),

где ai представляет собой значение 0 или 1 входной переменной xi.

Определение 4. Комбинационная схема содержит функциональное состязание при переходе из А в В, если для булевой функции, которую реализует схема, справедливы два условия:

1)f(A) = f(B) и

2)существуют единичные и нулевые значения функции в 2m- клетках подкуба (am+1, . . . ,an ).

Очевидно, что если схема содержит функциональное состязание при переходе из А в В, то должен быть некоторый набор для изменяющихся переменных x1, . . . , xm, для которого функция не равна f(А), f(В). Следовательно, существует возможность такого распределения задержек в схеме, при котором входные изменения достигают выхода в последовательности, вызывающей ложные импульсы. Данное состязание является внутренне присущим функции и не может быть устранено ее преобразованием, если допускается изменение входных сигналов в произвольном порядке.

Второй тип статических М-состязаний, называемый логическими состязаниями, похож на статические состязания в том, что оба типа состязаний могут быть устранены с помощью выбора подходящего выражения, используемого для построения схемы.

Определение 5. Комбинационная схема содержит логическое состязание при переходе из А в В, если справедливы следующие условия:

1)f(A) = f(B),

2)все 2m значений функции f в подкубе (am+1, . . . ,an ) одинако-

вы,

3)на выходе схемы может появиться ложный импульс.

150

Условие (2) эквивалентно утверждению, что изменение входов не дает функционального состязания.

Синтез схем, свободных от логических состязаний

Комбинационная схема может быть свободной от статических состязаний (m = 1), но все-таки содержать логические состязания. Пример такой схемы показан на рис. 6.7. Из диаграммы Вейча (см. рис. 6.7(а)) видно, что реализация схемы свободна от статических состязаний.

Рассмотрим переход из клетки "с" в клетку "b". На выходе схемы может появиться ложный нулевой импульс, если Y и Z изменят-

ся в 0 прежде, чем Y и Z изменятся в 1 (см. рис. 6.7(б)).

Рис. 6.7. Иллюстрация логического состязания

Таким образом, схема содержит логическое состязание при переходе из состояния X = Y = Z = W = 1 (клетка "с" на диаграмме Вейча) в состояние X = W = 1, Y= Z = 0 (клетка "в"). Переход из "a" в "d" также дает логическое состязание (см. рис. 6.7).

Для построения комбинационной схемы, свободной от всех логических состязаний, необходимо, чтобы выражение для функции включало все простые импликанты, т.е. являлось сокращенной ДНФ (КНФ).

151

Логические состязания в рассматриваемой схеме будут устранены добавлением элемента И, реализующим импликанту XW (см. пунктирное покрытие на рис. 6.7(а)).

Таким образом, функциональные состязания являются свойствами реализуемой функции, а логические состязания зависят от реализации функции.

Анализ комбинационных схем с целью выявления состязаний

В задачу анализа входит установление условий, при которых в данной схеме возможны состязания сигналов, и выяснение влияния ложных импульсов на функционирование схемы.

Для анализа схем при переходных процессах используют различные методы. Рассмотрим простейший из них — графический метод с использованием диаграмм Вейча. Для анализа схемы необходимо получить выражение функции, по которому построена схема. Затем на диаграмме Вейча следует отобразить покрытие единичных (нулевых) значений функции, соответствующее найденному выражению.

Например, для комбинационной схемы рис. 6.1(а) диаграмма Вейча с нанесенными покрытиями приведена на рис. 6.4.

После занесения на диаграмму Вейча функции в виде покрытий можно, рассматривая смежные входные состояния, выяснить, содержит схемная реализация функции статические состязания или нет. Аналогично определяют и логические состязания. Данный анализ совпадает по содержанию с теми примерами, которые рассматривались выше.

Если одинаковые значения функции на смежных наборах не входят в одно покрытие, то рассматриваемый переход содержит условия для состязаний сигналов в схеме.

Отметим, что комбинационная схема, построенная по ДНФ функции, свободна от статического риска в 0, а по КНФ — от статического риска в 1. Эти комбинационные схемы свободны также от динамических состязаний при изменении одного входного сигнала.

152