
- •List of Tables
- •List of Figures
- •Table of Notation
- •Preface
- •Boolean retrieval
- •An example information retrieval problem
- •Processing Boolean queries
- •The extended Boolean model versus ranked retrieval
- •References and further reading
- •The term vocabulary and postings lists
- •Document delineation and character sequence decoding
- •Obtaining the character sequence in a document
- •Choosing a document unit
- •Determining the vocabulary of terms
- •Tokenization
- •Dropping common terms: stop words
- •Normalization (equivalence classing of terms)
- •Stemming and lemmatization
- •Faster postings list intersection via skip pointers
- •Positional postings and phrase queries
- •Biword indexes
- •Positional indexes
- •Combination schemes
- •References and further reading
- •Dictionaries and tolerant retrieval
- •Search structures for dictionaries
- •Wildcard queries
- •General wildcard queries
- •Spelling correction
- •Implementing spelling correction
- •Forms of spelling correction
- •Edit distance
- •Context sensitive spelling correction
- •Phonetic correction
- •References and further reading
- •Index construction
- •Hardware basics
- •Blocked sort-based indexing
- •Single-pass in-memory indexing
- •Distributed indexing
- •Dynamic indexing
- •Other types of indexes
- •References and further reading
- •Index compression
- •Statistical properties of terms in information retrieval
- •Dictionary compression
- •Dictionary as a string
- •Blocked storage
- •Variable byte codes
- •References and further reading
- •Scoring, term weighting and the vector space model
- •Parametric and zone indexes
- •Weighted zone scoring
- •Learning weights
- •The optimal weight g
- •Term frequency and weighting
- •Inverse document frequency
- •The vector space model for scoring
- •Dot products
- •Queries as vectors
- •Computing vector scores
- •Sublinear tf scaling
- •Maximum tf normalization
- •Document and query weighting schemes
- •Pivoted normalized document length
- •References and further reading
- •Computing scores in a complete search system
- •Index elimination
- •Champion lists
- •Static quality scores and ordering
- •Impact ordering
- •Cluster pruning
- •Components of an information retrieval system
- •Tiered indexes
- •Designing parsing and scoring functions
- •Putting it all together
- •Vector space scoring and query operator interaction
- •References and further reading
- •Evaluation in information retrieval
- •Information retrieval system evaluation
- •Standard test collections
- •Evaluation of unranked retrieval sets
- •Evaluation of ranked retrieval results
- •Assessing relevance
- •A broader perspective: System quality and user utility
- •System issues
- •User utility
- •Results snippets
- •References and further reading
- •Relevance feedback and query expansion
- •Relevance feedback and pseudo relevance feedback
- •The Rocchio algorithm for relevance feedback
- •Probabilistic relevance feedback
- •When does relevance feedback work?
- •Relevance feedback on the web
- •Evaluation of relevance feedback strategies
- •Pseudo relevance feedback
- •Indirect relevance feedback
- •Summary
- •Global methods for query reformulation
- •Vocabulary tools for query reformulation
- •Query expansion
- •Automatic thesaurus generation
- •References and further reading
- •XML retrieval
- •Basic XML concepts
- •Challenges in XML retrieval
- •A vector space model for XML retrieval
- •Evaluation of XML retrieval
- •References and further reading
- •Exercises
- •Probabilistic information retrieval
- •Review of basic probability theory
- •The Probability Ranking Principle
- •The 1/0 loss case
- •The PRP with retrieval costs
- •The Binary Independence Model
- •Deriving a ranking function for query terms
- •Probability estimates in theory
- •Probability estimates in practice
- •Probabilistic approaches to relevance feedback
- •An appraisal and some extensions
- •An appraisal of probabilistic models
- •Bayesian network approaches to IR
- •References and further reading
- •Language models for information retrieval
- •Language models
- •Finite automata and language models
- •Types of language models
- •Multinomial distributions over words
- •The query likelihood model
- •Using query likelihood language models in IR
- •Estimating the query generation probability
- •Language modeling versus other approaches in IR
- •Extended language modeling approaches
- •References and further reading
- •Relation to multinomial unigram language model
- •The Bernoulli model
- •Properties of Naive Bayes
- •A variant of the multinomial model
- •Feature selection
- •Mutual information
- •Comparison of feature selection methods
- •References and further reading
- •Document representations and measures of relatedness in vector spaces
- •k nearest neighbor
- •Time complexity and optimality of kNN
- •The bias-variance tradeoff
- •References and further reading
- •Exercises
- •Support vector machines and machine learning on documents
- •Support vector machines: The linearly separable case
- •Extensions to the SVM model
- •Multiclass SVMs
- •Nonlinear SVMs
- •Experimental results
- •Machine learning methods in ad hoc information retrieval
- •Result ranking by machine learning
- •References and further reading
- •Flat clustering
- •Clustering in information retrieval
- •Problem statement
- •Evaluation of clustering
- •Cluster cardinality in K-means
- •Model-based clustering
- •References and further reading
- •Exercises
- •Hierarchical clustering
- •Hierarchical agglomerative clustering
- •Time complexity of HAC
- •Group-average agglomerative clustering
- •Centroid clustering
- •Optimality of HAC
- •Divisive clustering
- •Cluster labeling
- •Implementation notes
- •References and further reading
- •Exercises
- •Matrix decompositions and latent semantic indexing
- •Linear algebra review
- •Matrix decompositions
- •Term-document matrices and singular value decompositions
- •Low-rank approximations
- •Latent semantic indexing
- •References and further reading
- •Web search basics
- •Background and history
- •Web characteristics
- •The web graph
- •Spam
- •Advertising as the economic model
- •The search user experience
- •User query needs
- •Index size and estimation
- •Near-duplicates and shingling
- •References and further reading
- •Web crawling and indexes
- •Overview
- •Crawling
- •Crawler architecture
- •DNS resolution
- •The URL frontier
- •Distributing indexes
- •Connectivity servers
- •References and further reading
- •Link analysis
- •The Web as a graph
- •Anchor text and the web graph
- •PageRank
- •Markov chains
- •The PageRank computation
- •Hubs and Authorities
- •Choosing the subset of the Web
- •References and further reading
- •Bibliography
- •Author Index
206 |
10 XML retrieval |
book
chapter |
chapter |
chapter |
references |
title |
title |
title |
title |
FFT |
FFT |
encryption |
FFT |
q5 |
q6 |
|
d4 |
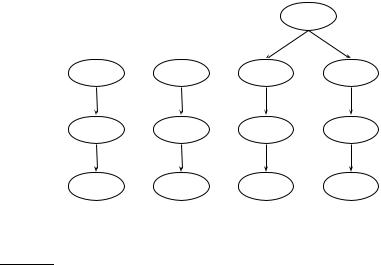
Figure 10.7 A structural mismatch between two queries and a document.
10.3A vector space model for XML retrieval
In this section, we present a simple vector space model for XML retrieval. It is not intended to be a complete description of a state-of-the-art system. Instead, we want to give the reader a flavor of how documents can be represented and retrieved in XML retrieval.
To take account of structure in retrieval in Figure 10.4, we want a book entitled Julius Caesar to be a match for q1 and no match (or a lower weighted match) for q2. In unstructured retrieval, there would be a single dimension of the vector space for Caesar. In XML retrieval, we must separate the title word Caesar from the author name Caesar. One way of doing this is to have each dimension of the vector space encode a word together with its position within the XML tree.
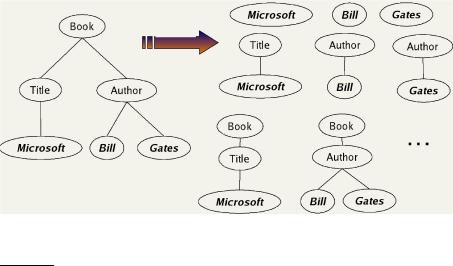
Figure 10.8 illustrates this representation. We first take each text node (which in our setup is always a leaf) and break it into multiple nodes, one for each word. So the leaf node Bill Gates is split into two leaves Bill and Gates. Next we define the dimensions of the vector space to be lexicalized subtrees of documents – subtrees that contain at least one vocabulary term. A subset of these possible lexicalized subtrees is shown in the figure, but there are others – e.g., the subtree corresponding to the whole document with the leaf node Gates removed. We can now represent queries and documents as vectors in this space of lexicalized subtrees and compute matches between them. This means that we can use the vector space formalism from Chapter 6 for XML retrieval. The main difference is that the dimensions of vector space
Online edition (c) 2009 Cambridge UP
10.3 A vector space model for XML retrieval |
207 |
Figure 10.8 A mapping of an XML document (left) to a set of lexicalized subtrees (right).
in unstructured retrieval are vocabulary terms whereas they are lexicalized subtrees in XML retrieval.
There is a tradeoff between the dimensionality of the space and accuracy of query results. If we trivially restrict dimensions to vocabulary terms, then we have a standard vector space retrieval system that will retrieve many documents that do not match the structure of the query (e.g., Gates in the title as opposed to the author element). If we create a separate dimension for each lexicalized subtree occurring in the collection, the dimensionality of the space becomes too large. A compromise is to index all paths that end in a single vocabulary term, in other words, all XML-context/term pairs.
STRUCTURAL TERM We call such an XML-context/term pair a structural term and denote it by hc, ti: a pair of XML-context c and vocabulary term t. The document in Figure 10.8 has nine structural terms. Seven are shown (e.g., "Bill" and
Author#"Bill") and two are not shown: /Book/Author#"Bill" and
/Book/Author#"Gates". The tree with the leaves Bill and Gates is a lexicalized subtree that is not a structural term. We use the previously introduced pseudo-XPath notation for structural terms.
As we discussed in the last section users are bad at remembering details about the schema and at constructing queries that comply with the schema. We will therefore interpret all queries as extended queries – that is, there can be an arbitrary number of intervening nodes in the document for any parentchild node pair in the query. For example, we interpret q5 in Figure 10.7 as
q6.
But we still prefer documents that match the query structure closely by
Online edition (c) 2009 Cambridge UP

208
CONTEXT
RESEMBLANCE
(10.1)
(10.2)
10 XML retrieval
inserting fewer additional nodes. We ensure that retrieval results respect this preference by computing a weight for each match. A simple measure of the similarity of a path cq in a query and a path cd in a document is the following context resemblance function CR:
CR(cq, cd) = ( |
|
1+|cq| |
if cq matches cd |
|
|
1+ c |
|
||
0 | |
d| |
if cq does not match cd |
||
where |cq| and |cd| are the number of nodes in the query path and document path, respectively, and cq matches cd iff we can transform cq into cd by inserting additional nodes. Two examples from Figure 10.6 are CR(cq4 , cd2 ) =
3/4 = 0.75 and CR(cq4 , cd3 ) = 3/5 = 0.6 where cq4 , cd2 and cd3 are the relevant paths from top to leaf node in q4, d2 and d3, respectively. The value of
CR(cq, cd) is 1.0 if q and d are identical.
The final score for a document is computed as a variant of the cosine mea- |
|||||||
sure (Equation (6.10), page 121), which we call SIMNOMERGE for reasons |
|||||||
that will become clear shortly. SIMNOMERGE is defined as follows: |
|||||||
SIMNOMERGE(q, d) = ∑ ∑ CR(c |
, c |
) ∑ weight(q, t, c |
) |
|
weight(d, t, cl) |
||
|
|
||||||
ck B cl B |
k |
l |
t V |
k |
|
q∑c B,t V weight2(d, t, c) |
|
where V is the vocabulary of non-structural terms; B is the set of all XML contexts; and weight(q, t, c) and weight(d, t, c) are the weights of term t in XML context c in query q and document d, respectively. We compute the weights using one of the weightings from Chapter 6, such as idft · wft,d. The inverse document frequency idft depends on which elements we use to compute dft as discussed in Section 10.2. The similarity measure SIMNOMERGE(q, d)
is not a true cosine measure since its value can be larger than 1.0 (Exer- q
cise 10.11). We divide by ∑c B,t V weight2(d, t, c) to normalize for doc-
ument length (Section 6.3.1, page 121). We have omitted query length nor-
malization to simplify the formula. It has no effect on ranking since, for q
a given query, the normalizer ∑c B,t V weight2(q, t, c) is the same for all
documents.
The algorithm for computing SIMNOMERGE for all documents in the col-
lection is shown in Figure 10.9. The array normalizer in Figure 10.9 contains q
∑c B,t V weight2(d, t, c) from Equation (10.2) for each document.
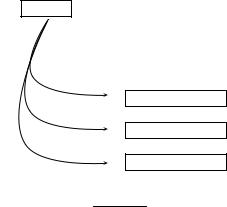
We give an example of how SIMNOMERGE computes query-document similarities in Figure 10.10. hc1, ti is one of the structural terms in the query. We successively retrieve all postings lists for structural terms hc′, ti with the same vocabulary term t. Three example postings lists are shown. For the first one, we have CR(c1, c1) = 1.0 since the two contexts are identical. The
Online edition (c) 2009 Cambridge UP
10.3 A vector space model for XML retrieval |
209 |
SCOREDOCUMENTSWITHSIMNOMERGE(q, B, V, N, normalizer)
1 for n ← 1 to N
2do score[n] ← 0
3for each hcq, ti q
4 do wq ← WEIGHT(q, t, cq)
5for each c B
6do if CR(cq, c) > 0
7 |
then postings ← GETPOSTINGS(hc, ti) |
8 |
for each posting postings |
9 |
do x ← CR(cq, c) wq weight( posting) |
10 |
score[docID( posting)] += x |
11for n ← 1 to N
12do score[n] ← score[n]/normalizer[n]
13return score
Figure 10.9 The algorithm for scoring documents with SIMNOMERGE.
query
hc1, ti
inverted index
CR(c1, c1) = 1.0
hc1, ti −→
CR(c1, c2) = 0
hc2, ti −→
CR(c1, c3) = 0.63
hc3, ti −→
hd1, 0.5i |
hd4, 0.1i |
hd9, 0.2i |
. . . |
|
|
|
|
hd2, 0.25i |
hd3, 0.1i |
hd12, 0.9i |
. . . |
|
|
|
|
hd3, 0.7i |
hd6, 0.8i |
hd9, 0.6i |
. . . |
Figure 10.10 Scoring of a query with one structural term in SIMNOMERGE.
next context has no context resemblance with c1: CR(c1, c2) = 0 and the corresponding postings list is ignored. The context match of c1 with c3 is 0.63>0 and it will be processed. In this example, the highest ranking document is d9 with a similarity of 1.0 × 0.2 + 0.63 × 0.6 = 0.578. To simplify the figure, the query weight of hc1, ti is assumed to be 1.0.
The query-document similarity function in Figure 10.9 is called SIMNOMERGE because different XML contexts are kept separate for the purpose of weighting. An alternative similarity function is SIMMERGE which relaxes the matching conditions of query and document further in the following three ways.
Online edition (c) 2009 Cambridge UP
