
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель

444 |
МАТЕМАТИЧЕСКИЙ АНАЛИЗ |
гл. VIII |
Но поскольку |−f(x)| = |f(x)|, мы имеем также формулу
bb
ZZ
− f(x) dx 6 |f(x)|dx,
aa
что дает вместе с формулой (15) более сильное неравенство, а именно
bb
ZZ
|
f(x) dx |
6 |f(x)|dx. |
(16) |
|
|
|
|
aa
§2. Производная
1.Производная как наклон. В то время как понятие интеграла своими корнями уходит в античную древность, другое основное понятие анализа — производная — было сформулировано только в XVII столетии знаменитым Ферма и другими. Сделанное Ньютоном и Лейбницем открытие органической связи между этими понятиями, казалось бы столь различными, способствовало небывалому развитию математической науки.
Ферма интересовался вопросом об определении наибольших и наименьших значений функции y = f(x). При изучении графика функции принято называть максимумом точку, расположенную выше всех других, а минимумом — точку, расположенную ниже всех других точек в
ееокрестности. На рис. 191 на стр. 365 точка B является максимумом, точка C — минимумом. Естественно при нахождении максимума или минимума использовать понятие касательной к кривой. Предположим, что график кривой нигде не образует острых углов и не обладает другими особенностями и что в каждой точке он имеет определенное направление, определяемое касательной прямой. В точках максимума или минимума касательная к кривой y = f(x) должна быть параллельна оси x; в противном случае кривая около этих точек или поднималась бы, или опускалась бы. Это замечание побуждает нас заняться общим вопросом об определении направления касательной к кривой y = f(x) в любой точке P этой кривой.
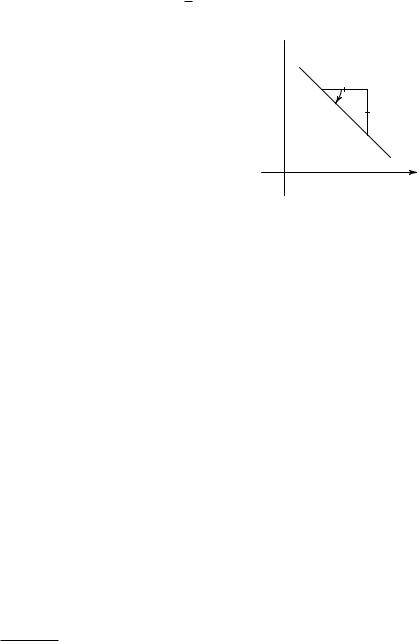
Чтобы охарактеризовать направление прямой в плоскости x, y, обыкновенно задается ее наклон, который представляет собой тангенс угла a между положительным направлением оси x и рассматриваемой прямой. Если P есть некоторая точка прямой L, продвигаемся вправо от нее до некоторой точки R, а затем вверх или вниз до точки Q, лежащей на
прямой, тогда наклон L равен tg a, т. е. RQP R . Отрезок P R предполагается
положительным, тогда как RQ — положительным или отрицательным в зависимости от того, будет ли он направлен вверх или вниз; таким образом, наклон дает нам подъем или падение на единицу длины по
§ 2 |
ПРОИЗВОДНАЯ |
445 |
горизонтали (при перемещении по прямой слева направо). На рис. 267 наклон первой прямой равен 23 , в то время как наклон второй прямой равен −1.
y 
R
P
Q
O |
x |
Рис. 267. Наклоны прямых
Под наклоном кривой в точке P мы подразумеваем наклон ее касательной в этой точке. Поскольку мы расположены принять понятие касательной как интуитивно данное, перед нами остается только задача — найти способ для вычисления наклона кривой. В настоящий момент мы встанем на именно такую точку зрения: более тщательный анализ относящихся сюда проблем будет произведен в дополнении к этой главе.
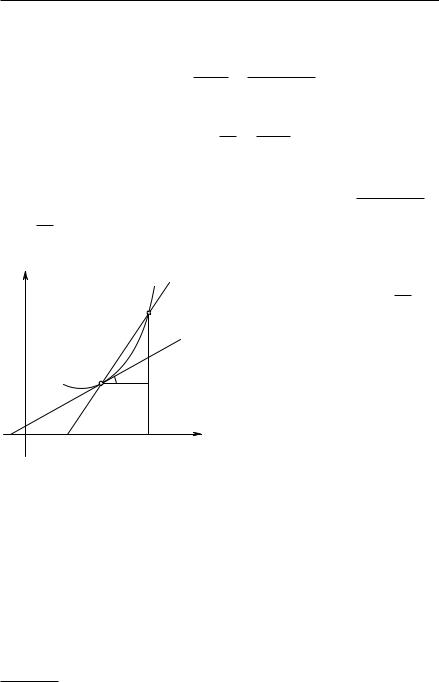
2. Производная как предел. Рассмотрение кривой y = f(x) только в одной ее точке P (x, y) не позволяет вычислить наклон кривой в этой точке. Необходимо прибегнуть к предельному процессу, сходному с процессом вычисления площади. Этот предельный процесс является основой дифференциального исчисления. Рассмотрим на данной кривой другую точку P1, близкую к P , с координатами x1, y1; обозначим прямую, проходящую через точки P и P1, буквой t1; эта прямая по отношению к нашей кривой является секущей, которая мало отличается от касательной к точке P , если только точка P1 близка к точке P . Обозначим угол между осью x и прямой t1 буквой a1. Заставим теперь x1 стремиться к x; тогда точка P1 будет двигаться по кривой к точке P и секущая t1 будет приближаться к некоторому предельному положению, которое и есть не что иное, как касательная t к нашей кривой в точке x. Если буквой a обозначить угол между осью x и касательной t, то при x1 → x будем иметь
y1 → y, P1 → P , t1 → t и a1 → a.
Касательная есть предел секущей, а наклон касательной есть предел наклона секущей1.
1Наши обозначения здесь слегка отличаются от обозначений главы VI, поскольку
446 |
МАТЕМАТИЧЕСКИЙ АНАЛИЗ |
|
|
гл. VIII |
||||
Хотя мы и не имеем явного выражения для наклона самой касатель- |
||||||||
ной t, зато наклон секущей t1 дается формулой |
|
|
|
|
||||
|
наклон t1 = y1 − y = f(x1) − f(x) ; |
|
|
|
||||
|
x1 − x |
|
x1 − x |
|
|
|
|
|
обозначая, как раньше, операцию образования разности символом |
, мы |
|||||||
получим |
y |
|
f(x) . |
|
|
|
|
|
|
наклон t1 = |
= |
|
|
|
|
||
|
|
x |
|
x |
|
|
|
|
Наклон секущей t1 есть «разностное отношение» — разность |
y значений |
|||||||
функции, деленная на разность x значений независимого переменно- |
||||||||
го. Сверх того, имеем наклон t = предел наклона t1 = lim f(x1) − f(x) = |
||||||||
|
xy , где пределы вычисляются при x1 → x, т. е. при |
x1 − x |
|
|||||
= lim |
x = x1 − x → |
|||||||
0. |
|
|
Касательная t к данной кри- |
|||||
|
|
|
||||||
y |
|
вой имеет наклон, равный преде- |
||||||
|
|
лу разностного отношения |
y |
при |
||||
|
|
|
|
|
|
|
x |
|
|
|
стремлении |
x = x1 − x к нулю. |
|||||
|
|
|
Первоначальная функция f(x) |
|||||
|
|
давала значение «высоты» различ- |
||||||
|
|
ных точек кривой y = f(x). Предпо- |
||||||
|
|
ложим теперь, что точка P движет- |
||||||
|
|
ся по кривой y = f(x). Тогда рас- |
||||||
|
|
сматриваемый наклон в точке P бу- |
||||||
|
x |
дет представлять некоторую новую |
||||||
O |
функцию от x, которую мы обозна- |
|||||||
|
|
чим через f0(x) и назовем производ- |
||||||
Рис. 268. Производная как предел |
ной от функции f(x). |
|
|
|
||||
|
|
|
Предельный процесс, с помощью |
|||||
которого получена производная, называется дифференцированием функ- |
||||||||
ции f(x). Этот процесс есть такая операция, которая по определенному |
||||||||
правилу сопоставляет данной функции f(x) некоторую другую функ- |
||||||||
цию f0(x). Подобным же образом при определении самой функции f(x) |
||||||||
было установлено правило, которое сопоставляло каждому значению |
||||||||
переменного x некоторое значение функции f(x). |
|
|
|
|
||||
Итак, |
|
|
|
|
|
|
|
|
f(x) есть высота кривой y = f(x) в точке x, |
|
|
|
|
||||
f0(x) есть наклон кривой y = f(x) в точке x. |
|
|
|
|
||||
Слово «дифференцирование» объясняется тем обстоятельством, что |
||||||||
f0(x) есть предел разности (differentia) f(x1) − f(x), деленной на раз- |
||||||||
там мы имели x → x1, где x1 постоянно. Никакой путаницы от этого изменения |
||||||||
обозначений не произойдет. |
|
|
|
|
|
|
|
|
§ 2 |
|
ПРОИЗВОДНАЯ |
|
|
|
447 |
|||
ность x1 − x: |
|
f(x1) − f(x) |
|
|
|
|
|
||
0 |
(x) = lim |
при |
x1 → x. |
|
|
(1) |
|||
f |
|
x1 − x |
|
|
|
||||
Другим часто употребляемым обозначением является |
|
|
|
||||||
|
|
f0(x) = Df(x), |
|
|
|
|
|||
где символ D есть первая буква слова differentia, что значит «разность»; |
|||||||||
кроме того, для производной от функции y = f(x) существуют еще обо- |
|||||||||
значения Лейбница |
|
|
df(x) , |
|
|
|
|
||
|
dy , |
или |
|
|
|
|
|||
|
dx |
|
|
dx |
|
|
|
|
|
которые мы подвергнем обсуждению в § 4, и намекающие на то, что про- |
|||||||||
изводная получается как предел разностного отношения |
y |
или |
f(x) 1. |
||||||
|
|
|
|
|
|
|
x |
|
x |
|
y |
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
x |
|
|
Рис. 269. Знак производной |
|
|
|
|||||
Условившись в том, что движение по кривой совершается в направлении возрастающих значений x, мы можем теперь заключить: то обстоятельство, что производная в некоторой точке положительна, f0(x) > 0, обозначает подъем кривой (значения y возрастают). Напротив, то обстоятельство, что производная отрицательна, f0(x) < 0, означает падение кривой (значения y убывают); наконец, если производная обращается в нуль, f0(x) = 0, то это обозначает горизонтальное направление кривой для соответствующего значения x. В точках максимума и минимума наклон должен быть равен нулю (рис. 269). Таким образом, решая урав-
нение
f0(x) = 0
относительно x, мы можем найти положение максимумов и минимумов, как это и было впервые сделано Ферма.
1В русском издании в дальнейшем используются именно эти, общепринятые у нас обозначения. — Прим. ред.

448 |
МАТЕМАТИЧЕСКИЙ АНАЛИЗ |
гл. VIII |
3. Примеры. Может показаться, что рассуждения, приведшие к определению (1), лишены всякого практического смысла. В самом деле, одна проблема подменена другой: вместо того чтобы искать наклон касательной к кривой y = f(x) в некоторой точке, мы должны вычислять предел (1), что с первого взгляда кажется одинаково трудным. Но как только мы откажемся от рассмотрении в общем виде и перейдем к отдельным функциям, мы получим весьма реальные результаты.
Простейшей из функций является функция f(x) = c, где c постоянно. График этой функции y = f(x) = c есть горизонтальная прямая, совпадающая со всеми своими касательными; очевидно, для всех значений x
имеет место соотношение
f0(x) = 0.
Это вытекает также и из определения (1); в самом деле,
y |
|
= |
f(x1) − f(x) |
= |
c − c |
= |
|
0 |
|
= 0. |
x |
|
x1 − x |
|
x1 − x x1 |
− x |
|
||||
Таким образом, получаем тривиальный результат:
lim |
f(x1) − f(x) |
= 0 при x1 → x. |
|||
x1 |
− |
x |
|
||
|
|
|
|
|
|
Вслед за этим рассмотрим простую функцию y = f(x) = x, графиком которой является биссектриса угла первого квадранта. Геометрически ясно, что для всех значений x
|
|
|
f0(x) = 1, |
|
|||||
а аналитическое определение (1) снова дает |
|
||||||||
|
f(x1) − f(x) |
= |
x1 − x |
= 1, |
|||||
так что |
x1 − x |
|
x1 − x |
|
|||||
f(x1) |
− f(x) |
|
|
|
|
||||
lim |
= 1 при |
x1 → x. |
|||||||
x1 |
− |
x |
|
||||||
|
|
|
|
|
|
|
|
||
Простейшим нетривиальным примером является дифференцирова-
ние функции
y = f(x) = x2,
что в сущности является нахождением наклона параболы. Это — простейший случай, на котором мы можем учиться совершать переход к пределу, когда результат с первого взгляда не очевиден. Мы имеем
y |
|
= |
f(x1) − f(x) |
= |
x12 − x2 |
. |
x |
|
x1 − x |
|
x1 − x |
||
Если бы мы попытались перейти к пределу непосредственно в числителе и в знаменателе, то получили бы не имеющее смысла выражение 00 . Но
этого затруднения можно избежать, сократив дробь на мешающий нам множитель x1 − x до перехода к пределу. (Такое сокращение законно,

§ 2 |
ПРОИЗВОДНАЯ |
449 |
так как при вычислении предела разностного отношения мы считаем, что x1 6= x, см. стр. 326.) Таким образом мы получаем результат
x12 − x2 |
= |
(x1 − x)(x1 + x) |
= x1 + x. |
x1 − x |
|
x1 − x |
|
После сокращения нахождение предела при x1 → x не представляет уже никаких трудностей. Этот предел получается путем простой «подстановки», так как разностное отношение в своем новом виде x1 + x непрерывно, а предел непрерывной функции при x1 → x есть просто значение этой функции при x1 = x; в нашем примере мы получаем непосредственно x + x = 2x и, следовательно, если f(x) = x2, то
f0(x) = 2x.
Совершенно аналогично мы можем доказать, что в случае функции f(x) = x3 мы будем иметь f0(x) = 3x2. В самом деле, отношение
y |
|
= |
f(x1) − f(x) |
= |
x13 − x3 |
x |
|
x1 − x |
|
x1 − x |
|
может быть упрощено по формуле
x31 − x3 = (x1 − x)(x21 + x1x + x2);
знаменатель x = x1 − x сокращается, и мы получаем непрерывное вы-
ражение
xy = x21 + x1x + x2.
При стремлении x1 к x это выражение стремится к сумме x2 + x2 + x2; в качестве предела получается выражение
f0(x) = 3x2.
И вообще, для функции
f(x) = xn,
где n — целое положительное, производная будет иметь вид
f0(x) = nxn−1.
Упражнение. Докажите этот результат. (Указание: примените алгебраическую формулу
xn1 − xn = (x1 − x)(xn1 −1 + xn1 −2x + xn1 −3x2 + . . . + x1xn−2 + xn−1).)
В качестве следующего примера, позволяющего непосредственно определить производную, рассмотрим функцию
y = f(x) = x1 .
Мы имеем
y = y1 − y |
= |
1 |
|
1 |
|
1 |
|
= x − x1 |
|
1 . |
|||||||
|
|
|
|
|
|
|
− |
|
· |
|
|
|
|
· |
|
|
|
x x1 − x |
|
x1 |
x |
x1 − x |
|
x1x |
x1 − x |
||||||||||
450 |
МАТЕМАТИЧЕСКИЙ АНАЛИЗ |
гл. VIII |
Сократим опять дробь и тогда получим
=− 1 x x1x
—выражение, опять-таки непрерывное в точке x1 = x; в качестве предела мы, следовательно, будем иметь
f0(x) = −x12 .
Само собой разумеется, что в данном случае ни производная, ни сама функция не определены в точке x = 0.
Упражнение. Докажите аналогичным способом, что функция f(x) =
1 |
имеет производную f0 |
2 |
; функция |
|
1 |
имеет производ- |
||||
|
|
(x) = − |
|
f(x) = |
|
|||||
|
x2 |
x3 |
xn |
|||||||
ную f0(x) = − |
n |
; функция f(x) = (1 + x)n |
имеет производную f0(x) = |
|||||||
xn+1 |
||||||||||
n(1 + x)n−1.
Продифференцируем теперь функцию
√
y = f(x) = x.
В качестве разностного отношения мы получаем
y = y1 − y x x1 − x
Воспользовавшись формулой x1 − сократить знаменатель с первым из непрерывное в точке x1 = x,
√√
=x1 − x. x1 − x
x = (√x1 − √x)(√x1 + √x), можно множителей и получить выражение,
|
|
|
|
|
|
|
|
y |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
= |
√ |
|
|
+ √ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Переход к пределу дает |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
f0(x) = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Упражнения. Докажите, что |
|
функция |
f(x) = |
1 |
имеет |
производ- |
|||||||||||||||||||||||||||
|
√ |
|
|||||||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||
ную f0(x) = − |
1 |
|
; докажите далее: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2(√ |
|
)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) что функция f(x) = √x |
имеет производную f |
0(x) = |
|
3 |
|
|
; |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
» f(x) = √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√x2 |
|
|
|
|
|||||||||
б) » |
1 − x2 |
|
» |
|
|
|
|
|
|
» |
f0(x) = − |
|
x |
|
|
|
; |
||||||||||||||||
|
|
|
|
|
|
|
√ |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
в) » |
» f(x) = √x |
» |
|
|
|
|
|
|
» |
f |
0(x) = |
|
|
n |
|
|
|
|
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n √xn−1 |
|||||||||
4. Производные от тригонометрических функций. Теперь мы приступим к чрезвычайно важному вопросу — к дифференцированию тригонометрических функций. Предварительно условимся, что измерение углов будем производить исключительно в радианах.

§ 2 ПРОИЗВОДНАЯ 451
Чтобы продифференцировать функцию y = f(x) = sin x, положим x1 − x = h, так что x1 = x + h и f(x1) = sin x1 = sin(x + h). Воспользовавшись тригонометрической формулой для синуса суммы двух углов, sin(A + B), мы получим
f(x1) = sin(x + h) = sin x cos h + cos x sin h.
Отсюда
f(x1) − f(x) |
= |
sin(x + h) − sin x |
= cos x · |
sin h |
+ sin x |
cos h |
− |
1 |
. (2) |
|
x1 − x |
h |
|
h |
h |
|
|||||
Если x1 стремится к x, то h стремится к 0, sin h стремится к 0, а cos h стремится к 1.
Далее, применяя результаты стр. 329–330, мы получим
lim |
sin h |
= 1 и |
lim |
cos h − 1 |
= 0. |
|
|||||
h→0 h |
|
h→0 |
h |
|
|
Правая часть соотношения (2) стремится, следовательно, к cos x, и мы получаем окончательный результат: функция f(x) = sin x имеет своей производной функцию f0(x) = cos x или, короче,
d(sin x) = cos x. dx
Упражнение. Докажите, что d(cos x) = − sin x. dx
Чтобы продифференцировать функцию f(x) = tg x, мы напишем tg x = cossin xx и получим, далее,
f(x + h) − f(x) |
= |
|
sin(x + h) |
|
− |
sin x |
|
· |
1 |
= |
|
|
|
|
|
|
||||
|
h |
cos(x + h) |
cos x |
|
h |
|
|
|
|
|
|
|||||||||
= |
sin(x + h) cos x − cos(x + h) sin x |
· |
|
|
|
|
1 |
= |
sin h |
· |
1 |
. |
||||||||
|
|
h |
|
|
|
cos(x + h) cos x |
h |
|
cos(x + h) cos x |
|||||||||||
(Последнее равенство получается с помощью формулы sin(A − B) = = sin A cos B − cos A sin B, где A = x + h, B = x.) Если h стремится к 0,
то |
sin h |
стремится к 1, cos(x + h) стремится к cos x, и отсюда мы делаем |
|||||||||||||
|
|||||||||||||||
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
||
заключение: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Производная функции f(x) = tg x есть функция f0(x) = |
1 |
|
, или |
|||||||||||
|
cos2 x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
d(tg x) |
= |
|
|
1 |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
dx |
|
|
cos2 x |
|
|
|
||||||
|
Упражнение. Докажите, что |
d(ctg x) |
1 |
. |
|
|
|
||||||||
|
|
|
|
|
= − |
|
|
|
|
||||||
|
|
|
dx |
sin2 x |
|
|
|
||||||||

452 МАТЕМАТИЧЕСКИЙ АНАЛИЗ гл. VIII
*5. Дифференцируемость и непрерывность. Необходимым условием дифференцируемости некоторой функции является ее непрерывность. В самом деле, если существует предел дифференциального
отношения |
y |
|
при стремлении x к нулю, то ясно, что приращение y |
|
x |
||||
|
|
|||
функции f(x) должно становиться неограниченно малым при стремлении x к нулю. Каждая дифференцируемая функция неизбежно является в то же время и непрерывной; поэтому, встречаясь в этой главе не раз с дифференцируемыми функциями, мы воздерживаемся от того, чтобы без особой необходимости постоянно упоминать, что они предполагаются непрерывными, или доказывать их непрерывность.
6. Производная и скорость. Вторая производная и ускорение. До сих пор понятие производной мы связывали с геометрическим представлением графика функции. Однако было бы грубой ошибкой ограничивать роль понятия производной одной лишь задачей об определении наклона касательной к данной кривой. Еще более важной с научной точки зрения задачей является вычисление скорости изменения какой бы то ни было величины f(t), меняющейся с течением времени. Именно с этой стороны Ньютон и подошел к дифференциальному исчислению. В частности, Ньютон стремился проанализировать явление скорости, рассматривая время и положение движущейся частицы как переменные величины (по выражению Ньютона, «флюэнты»). Когда некоторая частица движется вдоль оси x, то ее движение вполне определено, раз задана функция x = f(t), указывающая положение частицы x в любой момент времени t. «Равномерное движение» с постоянной скоростью b по оси x определяется линейной функцией x =
=a + bt, где a есть положение частицы в начальный момент (при t = 0). Движение частицы на плоскости описывается уже двумя функциями
x = f(t), y = g(t),
которые определяют ее координаты как функции времени. В частности, равномерному движению соответствуют две линейные функции
x = a + bt, y = c + dt,
где b и d — две «компоненты» постоянной скорости, а a и c — координаты начального положения частицы (при t = 0); траекторией частицы является прямая линия, уравнение которой
(x − a)d − (y − c)b = 0
получается путем исключения t из двух стоящих выше соотношений. Если частица движется в вертикальной плоскости x, y под действием
одной лишь силы тяжести, то движение ее (это доказывается в элементарной физике) определено двумя уравнениями
x = a + bt, y = c + dt − 12 gt2,

§ 2 |
ПРОИЗВОДНАЯ |
453 |
где a, b, c, d — постоянные величины, зависящие от состояния частицы в начальный момент, а g — ускорение силы тяжести, равное приблизительно 9,81, если время измеряется в секундах, а расстояние — в метрах. Траектория движения, получаемая путем исключения t из двух данных уравнений, есть парабола
|
d |
|
1 |
|
(x − a)2 |
|
y = c + |
b |
(x − a) − |
2 |
g |
b2 |
, |
если только b 6= 0; в противном случае траекторией является отрезок вертикальной оси.
Если частица вынуждена двигаться по некоторой данной кривой (подобно тому как поезд движется по рельсам), то движение ее может быть определено функцией s(t) (функцией времени t), равной длине дуги s, вычисляемой вдоль данной кривой от некоторой начальной точки P0 до положения частицы в точке P в момент времени t. Например, если речь идет о единичном круге x2 + y2 = 1, то функция s = ct определяет на этом круге равномерное вращательное движение со скоростью c.
* Упражнение. Начертите траектории плоских движений, заданных уравнениями: 1) x = sin t, y = cos t; 2) x = sin 2t, y = cos 3t; 3) x = sin 2t, y = = 2 sin 3t; 4) в описанном выше параболическом движении предположите начальное положение частицы (при t = 0) в начале координат и считайте b > 0, d > 0. Найдите координаты самой высокой точки траектории. Найдите время t и значение x, соответствующие вторичному пересечению траектории с осью x.
Первой целью, которую поставил себе Ньютон, было нахождение скорости частицы, движущейся неравномерно. Рассмотрим для простоты движение частицы вдоль некоторой прямой линии, заданное функцией x = f(t). Если бы движение было равномерным, т. е. совершалось с постоянной скоростью, то эту скорость можно было бы найти, взяв два момента времени t и t1 и соответствующие им положения частиц f(t) и f(t1) и составив отношение
v = скорость = |
расстояние |
= |
x1 |
− x |
= |
f(t1) − f(t) |
. |
(3) |
|
время |
t1 |
||||||||
|
|
− t |
|
t1 − t |
|
||||
Например, если t измерено в часах, а x в километрах, то при t1 − t = 1 разность x1 − x будет число километров, пройденных за 1 час, а v — скорость (километров в час). Говоря, что скорость есть величина постоянная, имеют в виду лишь то, что разностное отношение
f(t1) − f(t) |
(4) |
t1 − t |
|
не изменяется при любых значениях t и t1. Но если движение неравномерно (что имеет, например, место при свободном падении тела, скорость которого по мере падения возрастает), то отношение (4) не дает значения скорости в момент t, а представляет собой то, что принято называть

454 |
МАТЕМАТИЧЕСКИЙ АНАЛИЗ |
гл. VIII |
средней скоростью в промежутке времени от t до t1. Чтобы получить скорость в момент t, нужно вычислить предел средней скорости при стремлении t1 к t. Таким образом, вместе с Ньютоном определим скорость так:
скорость в момент t = lim |
f(t1) − f(t) |
= f0(t). |
(5) |
t1→t |
t1 − t |
|
|
Другими словами, скорость есть производная от «пройденного пути» (координаты частицы на прямой) по времени, или «мгновенная скорость изменения» пути по отношению ко времени — в противоположность средней скорости изменения, определяемой по формуле (4).
Скорость изменения самой скорости называется ускорением. Ускорение — это просто производная от производной; она обычно обозначается символом f00(t) и называется второй производной от функции f(t).
Галилей заметил, что вертикальное расстояние x, проходимое при свободном падении тела в течение времени t, выражается формулой
x = f(t) = |
1 |
gt2 |
, |
(6) |
|
2 |
|||||
|
|
|
|
где g есть ускорение силы тяжести. Из формулы (6), путем дифференцирования ее, можно получить скорость v тела в момент времени t; эта скорость выражается формулой
v = f0(t) = gt, |
(7) |
а ускорение a, которое постоянно,— формулой
a = f00(t) = g.
Предположим, что нужно найти скорость тела через 2 секунды после начала падения. Найдем сначала среднюю скорость за промежуток времени от t = 2 до t = 2,1:
|
1 |
g · (2,1)2 − |
1 |
g · 22 |
|
4,905 · 0,41 |
|
|
2 |
2 |
= |
= 20,11 (метров в секунду). |
|||
|
|
2,1 − 2 |
|
|
|||
|
|
|
|
|
0,1 |
|
Подставляя же в формулу (7) значение t = 2, мы найдем, что значение мгновенной скорости в конце второй секунды равно 19,62 (метров в секунду).
Упражнение. Какова средняя скорость тела за промежуток времени от t = 2 до t = 2,01, от t = 2 до t = 2,001?
При движении точки на плоскости две производные f0(t) и g0(t) двух функций x = f(t) и y = g(t) определяют компоненты скорости. При движении вдоль заданной кривой скорость нужно определить как производную от функции s = f(t), где s — длина дуги.
§ 2 |
ПРОИЗВОДНАЯ |
455 |
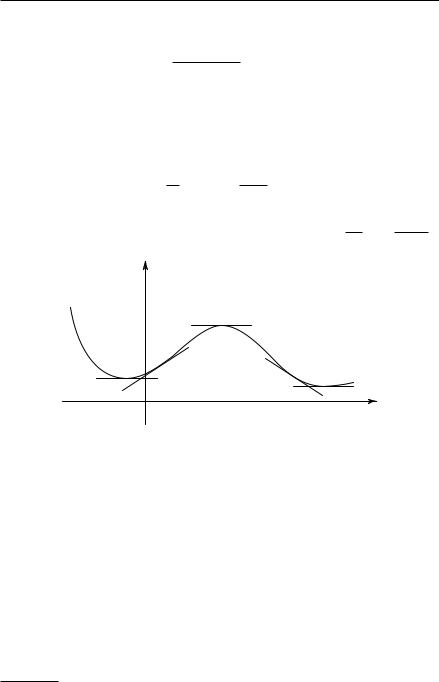
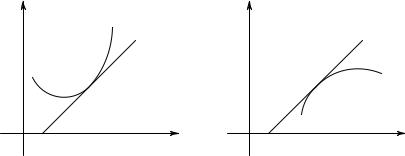
7. Геометрический смысл второй производной. Вторая производная f00(x) имеет также важное значение в анализе и в геометрии; в самом деле, представляя собой скорость изменения наклона f0(x) кривой y = f(x), вторая производная дает указание на то, как изогнута кривая. Если в некотором промежутке вторая производная больше нуля, то скорость изменения наклона f0(x) положительна. Положительный знак скорости изменения некоторой функции указывает на то, что эта функция возрастает с возрастанием аргумента x. Следовательно, неравенство f00(x) > 0 указывает на то, что наклон f0(x) есть возрастающая функция x и, значит, при увеличении x кривая становится более крутой там, где наклон ее положителен, и более пологой там, где наклон отрицателен. Условимся говорить, что в этом случае кривая вогнута (рис. 270). Аналогично, если f00(x) < 0, то будем говорить, что кривая y = f(x) выпукла (рис. 271).
y |
y |
f (x) 0 |
f (x) 0 |
O |
x |
O |
x |
|
Рис. 270–271. Вогнутость и выпуклость кривой |
|
|
Парабола y = f(x) = x2 всюду вогнута, так как ее вторая производная (f00(x) = 2) всегда положительна. Кривая y = f(x) = x3 вогнута при x > 0 и выпукла при x < 0 (рис. 153); это видно по ее второй производной, f00(x) = 6x, в чем читатель может легко убедиться сам. Между прочим, при x = 0 имеем f0(x) = 3x2 = 0 (но нет ни минимума, ни максимума!), а также f00(x) = 0 при x = 0. Эта точка называется точкой перегиба. В точках, которые так называются, касательная (в данном случае ось x) пересекает кривую.
Если буква s обозначает длину дуги кривой, а буква a — угол наклона, то функция a = h(s) есть функция переменного s. При передвижении точки по кривой функция a = h(s) будет меняться. Скорость этого изменения h0(s) принято называть кривизной кривой в точке, для которой длина дуги равна s. Без доказательства отметим, что кривизна k может быть выражена с помощью первой и второй производных от функ-
