
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель

98 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
ное число. Не составит труда проверить, что определение Дедекинда согласуется с определением, в основе которого находятся вложенные отрезки: из всякой последовательности вложенных отрезков I1, I2, I3,
. . . мы получаем сечение, если отнесем к классу A все те рациональные числа, которые меньше, чем левый конец хотя бы одного интервала In,
кклассу B — все прочие рациональные числа.
Вфилософском отношении определение иррациональных чисел по Дедекинду находится на более высоком уровне абстракции, так как оно не ограничивает ни в чем того математического закона, который определяет классы A и B. Другой, более конкретный метод для определения континуума действительных чисел принадлежит Георгу Кантору (1845–1918). На первый взгляд резко отличный как от метода вложенных отрезков, так и от метода сечений, он, однако, эквивалентен любому из них в том смысле, что числовой континуум, получающийся на основе всех трех методов, обладает одними и теми же свойствами. Идея Кантора базируется на тех обстоятельствах, что 1) действительные числа можно трактовать как бесконечные десятичные дроби, 2) бесконечные десятичные дроби можно рассматривать как пределы конечных десятичных дробей. Чтобы не связывать себя зависимостью от десятичных дробей, мы, следуя Кантору, принимаем, что всякая «сходящаяся» последовательность рациональных чисел a1, a2, a3, . . . определяет действительное число. При этом «сходимость» понимается в том смысле, что разность (am − an) между двумя членами последовательности стремится к нулю, если m и n одновременно и независимо друг от друга неограниченно возрастают. (Как раз последовательные десятичные приближения обладают
этим свойством: любые два из них после n-го отличаются меньше чем на 10−n.) Так как одно и то же действительное число по методу Кантора может быть определяемо самыми разнообразными последовательностями рациональных чисел, то приходится добавить, что две последовательности a1, a2, a3, . . . и b1, b2, b3, . . . определяют одно и то же действительное число, если разность an − bn стремится к нулю при неограниченном возрастании n. Идя по пути, намеченному Кантором, нетрудно определить сложение
ит. д.
§3. Замечания из области аналитической геометрии1
1.Основной принцип. Уже начиная с XVII в. числовой континуум, принимаемый как нечто само собой разумеющееся или же подвергаемый более или менее поверхностному критическому анализу, стал основой математики, в частности, аналитической геометрии и дифференциального и интегрального исчислений.
Введение числового континуума дает возможность сопоставить
1 Читателю, не вполне освоившемуся с предметом этого параграфа, рекомендуется обратиться к упражнениям, которые помещены в приложении в конце книги, стр. 513 и дальше.
§ 3 |
ЗАМЕЧАНИЯ ИЗ ОБЛАСТИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ |
99 |
|||||
каждому отрезку прямой в качестве его «длины» некоторое опре- |
|||||||
деленное действительное число. Но можно пойти и дальше. Не только |
|||||||
длина, но и всякий вообще геометрический объект, всякая геомет- |
|||||||
рическая операция могут найти свое место в царстве чисел. Ре- |
|||||||
шительные шаги в направлении арифметизации геометрии был сде- |
|||||||
ланы не позднее 1629 г. Ферма (1601–1665) и в 1637 г. Декартом |
|||||||
(1596–1650). Основная идея аналитической геометрии заключается в |
|||||||
использовании «координат» — чисел, |
связанных |
(координированных) |
|||||
с данным геометрическим объектом и полностью этот объект ха- |
|||||||
рактеризующих. Большинству читателей известны так называемые |
|||||||
прямоугольные, или декартовы, координаты, служащие для того, что- |
|||||||
бы фиксировать положение произвольной точки на плоскости. Мы |
|||||||
исходим из двух неподвижных взаимно перпендикулярных прямых |
|||||||
на плоскости, «оси x» и «оси y», и к ним относим каждую точку. |
|||||||
Эти оси рассматриваются как ориентированные числовые прямые, |
|||||||
причем измерение совершается с по- |
|
|
|
|
|
||
мощью одного и того же единично- |
y |
|
|
|
|
||
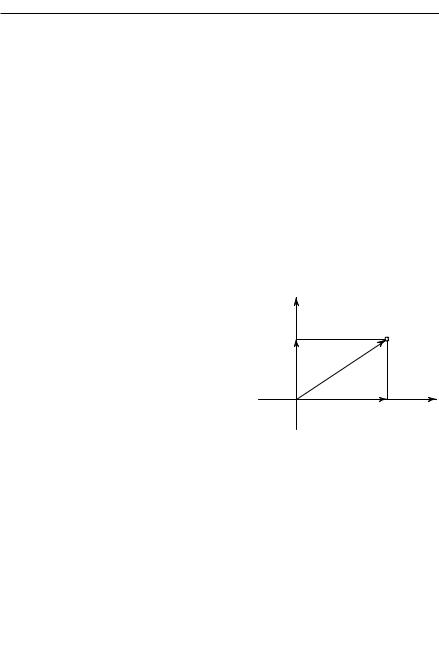
го отрезка. Каждой точке P (рис. 12) |
|
|
|
|
|
||
сопоставлены две координаты x и y. |
Q |
|
|
P |
|
||
Они получаются следующим образом. |
|
|
|
|
|||
|
|
|
|
|
|||
Рассмотрим ориентированный отрезок |
y |
|
|
|
|
||
(вектор), идущий из «начала» O в точ- |
|
|
|
|
|
||
ку |
P , и затем спроектируем ортого- |
O |
x |
P |
|
x |
|
нально этот вектор на обе оси, полу- |
|||||||
|
|
|
|
||||
чая ориентированный отрезок OP 0 на |
|
|
|
|
|
||
оси x и такой же отрезок OQ0 на оси y. |
Рис. 12. Прямоугольные коорди- |
||||||
Два числа x и y, измеряющие соответ- |
|
наты точки |
|
|
|
||
ственно ориентированную длину отрез- |
|
|
|
|
|
||
ков OP 0 и OQ0, называются координатами точки P . Обратно, если x |
|||||||
и y — два произвольных наперед заданных числа, то соответствующая |
|||||||
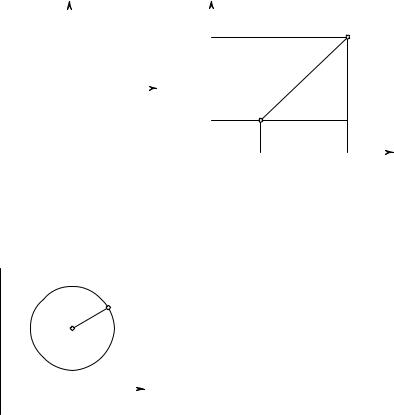
точка P определяется однозначно. Если числа x и y оба положительные, |
|||||||
то P попадает в первый квадрант координатной системы (рис. 13); если |
|||||||
оба отрицательные, то в третий; если x положительно, а y отрицательно, |
|||||||
то в четвертый, и, наконец, если x отрицательно, а y положительно, то |
|||||||
во второй. |
|
|
|
|
|
||
|
Расстояние между точкой P1 с координатами x1, y1 и точкой P2 с |
||||||
координатами x2, y2 дается формулой |
|
|
|
|
|
||
|
d2 = (x1 − x2)2 + (y1 − y2)2. |
|
|
|
(1) |
||
Это немедленно следует из пифагоровой теоремы (рис. 14). |
|
|
|
||||
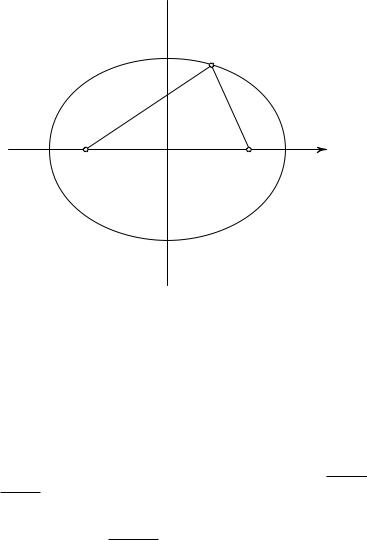
2. Уравнения прямых и кривых линий. Если C есть неподвижная точка с координатами x = a, y = b, то геометрическое место всех точек P , находящихся от точки C на данном расстоянии r, есть окруж-
100 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
||||||||
|
|
y |
|
|
y |
|
|
(x2 , y2) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
II |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
y2 |
y1 |
|
|
|
|
|
|
|
|
|
|||
|
|
O |
x |
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
(x1 , y1) |
x2 |
x1 |
|
|
|
|
III |
IV |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
x1 |
x2 |
x |
||
|
|
Рис. 13. Четыре квадранта |
Рис. |
14. Расстояние |
между |
двумя |
||||
|
|
|
|
|
|
|
точками |
|
|
|
ность с центром C и радиусом r. Из формулы для расстояния между двумя точками (1) следует, что точки y  этой окружности имеют координаты x,
этой окружности имеют координаты x,
y, удовлетворяющие уравнению
|
R |
|
|
2 |
2 |
2 |
|
r |
|
|
(x − a) + (y − b) |
|
= r . |
(2) |
|
|
|
|
|
||||
C |
|
|
Это уравнение называется уравнени- |
||||
|
|
|
ем окружности, так как оно выража- |
||||
|
|
|
ет полное (необходимое и достаточное) |
||||
|
|
|
условие |
того, что точка |
P с |
коорди- |
|
|
|
|
натами |
x, y лежит на |
окружности с |
||
O |
|
x |
|||||
|
|
|
центром C и радиусом r. Если скобки |
||||
Рис. 15. Окружность |
|
раскрыть, уравнение принимает вид |
|||||
|
|
x2 + y2 − 2ax − 2by = k, |
(3) |
||||
|
|
|
|
||||
где k = r2 − a2 − b2. Обратно, если задано уравнение вида (3), причем a, b и k — произвольные постоянные и сумма k + a2 + b2 положительна, то с помощью алгебраической процедуры «дополнения до квадрата» мы можем написать то же уравнение в форме
(x − a)2 + (y − b)2 = r2,
где r2 = k + a2 + b2. И тогда ясно, что уравнение (3) определяет окружность радиуса r, центр которой — в точке C с координатами a, b.
Уравнение прямой линий еще проще по своей форме. Так, например, уравнение оси x имеет вид y = 0, так как координата y равна нулю для всех точек этой оси и ни для каких иных точек. Точно так же ось y имеет уравнение x = 0. Прямые, проходящие через начало и делящие пополам углы между осями, имеют уравнения x = y и x = −y. Легко показать, что всякая прямая линия имеет уравнение вида
ax + by = c, |
(4) |
§ 3 |
ЗАМЕЧАНИЯ ИЗ ОБЛАСТИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ |
101 |
где a, b, c — постоянные, характеризующие эту прямую. Как и в других случаях, смысл уравнения (4) тот, что пары действительных чисел x и y, удовлетворяющих этому уравнению, являются координатами некоторой точки на прямой, и обратно.
y 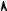
B
A F |
F |
A x |
B
Рис. 16. Эллипс с фокусами
Может быть, читатель учил в школе, что уравнение вида
x2 |
+ |
y2 |
= 1 |
(5) |
|
p2 |
q2 |
||||
|
|
|
представляет эллипс (рис. 16). Эта кривая пересекает ось x в точках A(p, 0) и A0(−p, 0) и ось y в точках B(0, q) и B0(0, −q). (Обозначение P (x, y) или, еще короче, (x, y), вводится ради краткости и должно быть расшифровано так: «точка P с координатами x и y».) Если p > q, то отрезок AA0 длины 2p называется большой осью эллипса, а отрезок BB0 длины 2q — его малой осью. Эллипс есть геометрическое место точек P , сумма расстояний которых от точек F (√p2 − q2, 0) и F 0(−√p2 − q2, 0) равна 2p. Читатель сможет проверить это в качестве упражнения, применяя формулу (1). Точки F и F 0 называются фокусами
эллипса, а отношение e = |
p |
p2p− q2 |
называется его эксцентриситетом. |
|||||
Уравнение вида |
2 |
|
2 |
|
|
|||
|
|
|
x |
− |
y |
= 1 |
(6) |
|
|
|
|
p2 |
q2 |
||||
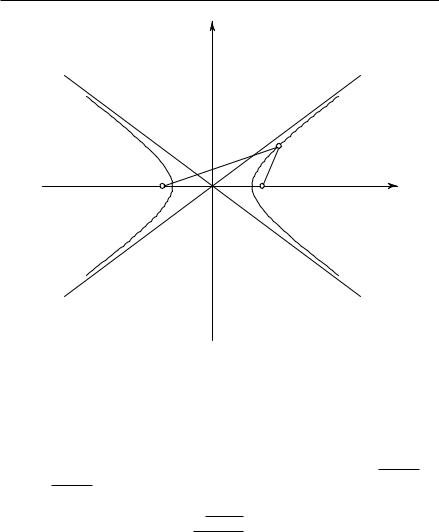
представляет гиперболу. Эта кривая состоит из двух ветвей, пересе-
102 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
|||
|
|
|
y |
|
|
|
F |
A |
A |
F |
x |
|
Рис. 17. Гипербола с фокусами |
|
|||
кающих ось x соответственно в точках A(p, 0) и A0(−p, 0) (рис. 17). Отрезок AA0 длины 2p называется «действительной» осью гиперболы. Гипербола, удаляясь в бесконечность, приближается к двум прямым qx ± py = 0, но так с ними и не пересекается; эти прямые называ-
ются асимптотами гиперболы. Гипербола есть геометрическое место
√
точек P , разность расстояний которых до двух точек F ( p2 + q2, 0) и F 0(−√p2 + q2, 0) по абсолютной величине равна 2p. Эти точки в случае гиперболы тоже называются фокусами; под эксцентриситетом гипер-
p
болы понимают отношение e = p2 + q2 . p
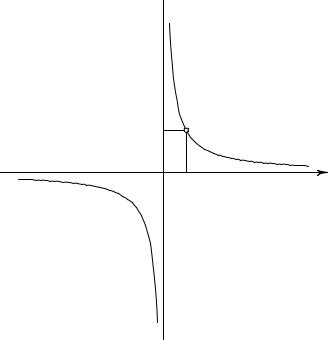
Уравнение
xy = 1 |
(7) |
также определяет гиперболу, но такую, для которой асимптотами являются две оси (рис. 18). Уравнение этой «равносторонней» гиперболы геометрически означает, что площадь прямоугольника OP 0P Q0 (см. рис. 12), связанного с точкой P , для всякой точки P кривой равна 1. Равносторонняя гипербола несколько более общего вида
xy = c, |
(7a) |
где c — постоянная, представляет собой частный случай гиперболы в
§ 3 |
ЗАМЕЧАНИЯ ИЗ ОБЛАСТИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ |
103 |
том же смысле, в каком окружность представляет собой частный случай эллипса. Отличительная характеристика равносторонней гиперболы заключается в том, что ее две асимптоты (в нашем случае — две оси) взаимно перпендикулярны.
y 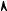
P
x
Рис. 18. Равносторонняя гипербола. Площадь прямоугольника, определенного точкой P (x, y), равна 1
Во всем этом для нас самым интересным является руководящая идея: геометрические объекты могут полностью описываться в арифметической или алгебраической форме. То же справедливо и относительно геометрических операций. Например, если нам требуется найти точки пересечения двух прямых, то мы рассматриваем два их уравнения
ax + by = c,
(8)
a0x + b0y = c0,
и для нахождения общей точки этих двух прямых достаточно решить систему (8); решение дает нам координаты искомой точки. Таким же образом точки пересечения двух произвольных кривых (скажем, окружности x2 + y2 − 2ax − 2by = k и прямой ax + by = c) находятся посредством совместного решения их уравнений.
