§ 2 ПРЕДЕЛЫ 317

что путем инверсии совокупность прямых и окружностей преобразуется в совокупность опять-таки прямых и окружностей.

переводится в четверку точек на оси x с тем же двойным отношением (см. стр. 216).

§2. Пределы

1.Предел последовательности an. Определение непрерывности функции, как мы это уже видели в § 1, основывается на понятии предела. До сих пор мы пользовались этим понятием в более или менее интуитивной форме. В настоящем и последующих разделах мы введем его более систематическим путем. Поскольку последовательности несколько проще, чем функции непрерывного переменного, мы начнем с изучения последовательностей.

В главе II мы имели дело с числовыми последовательностями an и изучали их пределы при условии, что n неограниченно увеличивается или «стремится» к бесконечности. Например, последовательность с об-

Постараемся выразить точно, что под этим подразумевается. При продвижении по последовательности все дальше и дальше мы видим, что члены становятся все меньше и меньше. После 100-го члена члены уже

меньше 1001 , после 1000-го — меньше 10001 , и т. д. Ни один из членов не равен в действительности 0. Но если мы продвинемся достаточно далеко

по последовательности (1), то мы можем быть уверены, что каждый из

еечленов будет отличаться от 0 сколь угодно мало.

Вэтом объяснении может смущать единственно то, что смысл подчеркнутых слов не вполне ясен. Что значит «достаточно далеко» и что значит «сколь угодно мало»? Если мы сумеем придать точный смысл этим выражениям, то этим самым будет установлен точный смысл понятия предела последовательности.

Геометрическая интерпретация поможет нам разобраться в интересующем нас вопросе. Если мы изобразим члены последовательности (1) в виде соответствующих им точек на числовой оси, то заметим, что члены последовательности в нашем примере «накопляются» или «сгущаются» около точки 0. Выберем на числовой оси некоторый интервал I с центром в точке 0 и общей длиной 2e, так чтобы интервал простирался на

расстояние e с каждой стороны от точки 0. Если мы возьмем e = 10, то, конечно, все члены an = n1 нашей последовательности будут лежать

внутри интервала I. Если же мы возьмем e = 101 , то несколько первых

членов окажутся лежащими вне интервала I; однако все члены, начиная

с a11, а именно

111 , 121 , 131 , 141 , . . . ,

будут лежать внутри I. Даже при e = 10001 лишь первая тысяча членов последовательности не попадет внутрь интервала I, тогда как бесконеч-

ное множество членов, начиная с a1001,

a1001, a1002, a1003, . . .

окажется внутри него. Ясно, что это рассуждение справедливо для любого положительного числа e: если положительное e выбрано, то независимо от того, как оно мало, мы всегда можем подобрать настолько большое целое число N, что

N1 < e.

Отсюда следует, что все члены an последовательности, для которых n > N, будут лежать внутри интервала I, и только конечное число членов a1, a2, . . ., aN−1 может лежать вне его. Основные моменты здесь таковы: во-первых, длина интервала I определяется произвольно посредством выбора e. Затем может быть подобрано подходящее целое число N. Этот процесс первоначального выбора числа e и последующего подбора целого числа N может быть осуществлен при любом положительном e независимо от его малости; тем самым устанавливается точный смысл утверждения, что «все члены последовательности (1) отличаются от 0 сколь угодно мало, если только мы достаточно далеко продвинемся по последовательности».

Подведем итоги: пусть e — какое-нибудь положительное число. Тогда мы можем подобрать такое целое положительное число N, что все члены an последовательности (1), для которых n > N, будут лежать внутри интервала I длины 2e с центром в точке e. Таков смысл предельного соотношения (2).

Опираясь на этот пример, мы можем теперь дать точное определение следующего общего утверждения: «Последовательность действительных чисел a1, a2, a3, . . . имеет предел a». Число a мы заключаем внутрь некоторого интервала I числовой оси: если этот интервал мал, то некоторые числа an могут лежать вне этого интервала, но как только n становится достаточно большим, скажем, б´ольшим или равным некоторому числу N, то все числа an, для которых n > N, должны лежать внутри

интервала I. Конечно, может случиться, что придется брать очень большое целое число N, если интервал I выбран очень малым; однако, как бы мал ни был этот интервал I, такое целое число N должно существовать, раз предполагается, что последовательность имеет предел.

Тот факт, что последовательность an имеет предел a, выражается символически следующей записью:

lim an = a при n → ∞, lim an = a,

n→∞

или просто

an → a при n → ∞

(«предел an равен a», или «an стремится к пределу a»). Если последовательность имеет предел в указанном смысле, она называется сходящейся. Определение сходимости последовательности an можно сформулировать более сжато, а именно следующим образом:

Последовательность a1, a2, a3, . . . имеет предел a при неограниченном возрастании n, если каждому сколь угодно малому положительному числу e можно поставить в соответствие такое целое положительное число N (зависящее от e), что неравенство

выполняется для всех значений

n > N.

Такова общая, «абстрактная» формулировка понятия предела последовательности. Немудрено, если тот, кто встречается с ней впервые, не может сразу схватить и исчерпать ее содержание. К несчастью, авторы некоторых руководств, стоящие на позиции, граничащей со снобизмом, преподносят читателю это определение без тщательной подготовки, как будто снизойти до разъяснений ниже достоинства математика.

Определение предполагает своего рода дискуссию между двумя лицами A и B. A выдвигает требование: заданная величина a должна быть приближена числами an так, чтобы ошибка не превышала границы e = e1; B отвечает на это требование указанием, что существует такое целое N = N1, что все члены an, следующие за aN1 , удовлетворяют этому условию. Тогда A становится более требовательным и предлагает новую, меньшую границу e = e2; B снова встречает это требование подбором некоторого, может быть значительно большего, целого числа N = N2, обладающего аналогичным свойством, и т. д. Если B может удовлетворить A независимо от того, какую малую границу назначает A, то мы имеем дело с положением, которое кратко выражается соотношением: an → a.

Имеется определенная психологическая трудность в том, чтобы составить правильное представление о понятии предела. Наша интуиция

320 ФУНКЦИИ И ПРЕДЕЛЫ гл. VI

предполагает «динамическую» идею предела как результат процесса «движения»: мы продвигаемся по ряду целых чисел 1, 2, 3, . . . , n, . . .

и при этом наблюдаем за поведением последовательности an. Мы ждем, что числа an должны все меньше и меньше отличаться от числа a. Но эта «естественная» точка зрения не поддается ясной математической формулировке. Чтобы прийти к точному определению, надо обратить ход рассуждения: вместо того чтобы прежде всего обращаться к независимому переменному n, а затем уже к переменному an, мы должны основывать наше определение на том, что следует делать, если мы по существу хотим проконтролировать утверждение an → a. При такой постановке вопроса мы прежде всего должны выбрать произвольно малый интервал около a и затем решить: можем ли мы добиться, чтобы an с помощью выбора достаточно большого n в него попало. Затем, вводя символы e и N для обозначения «произвольно малого интервала» и «достаточно большого n», мы приходим к точному определению предела.

Обращаясь теперь к другому примеру, рассмотрим последователь-

при n > 10. Если вы усилите ваше требование, выбирая e = 10001 , то я снова могу ему удовлетворить, выбирая N = 1000; и так далее — для

любого положительного числа e, которое вы пожелаете выбрать, независимо от его малости: действительно, мне только нужно будет вы-

1

брать любое целое N, большее чем e . Этот процесс, заключающийся,

во-первых, в выборе произвольно малого интервала длины 2e вокруг числа a и, во-вторых, в доказательстве того, что все члены последовательности an находятся на расстоянии, меньшем чем e от a, раз только мы продвинемся достаточно далеко по последовательности, и есть не что иное, как подробное описание того факта, что an → a. Если члены последовательности a1, a2, a3, . . . представлены в виде бесконечных десятичных дробей, то утверждение

lim an = a

обозначает попросту то, что для любого целого положительного m первые m цифр числа an совпадают с первыми m цифрами бесконечного десятичного разложения числа a, раз только n выбрано достаточно боль-

шим, скажем, б´ольшим некоторого значения N (зависящего от m).1 Это просто соответствует выбору e в форме 10−m.

Существует другое, и очень выразительное, определение понятия предела. Если lim an = a и если мы заключим число a в интервал I, то, независимо от малости интервала I все числа an при n, б´ольшем некоторого целого числа N, будут лежать в интервале I, так что не больше чем конечное число N − 1 членов из числа следующих:

a1, a2, a3, . . . , aN−1,

могут лежать вне интервала I. Если интервал I очень мал, то число N может быть очень большим, скажем, равным 100 или даже 1000 биллионам, и все же лишь конечное число членов последовательности будет лежать вне интервала I, в то время как бесконечное множество оставшихся членов попадет в интервал I. Можно условиться говорить о членах некоторой бесконечной последовательности, что «почти все» они обладают некоторым свойством, если лишь конечное число их (неважно, как оно будет велико) не обладает этим свойством. Так, например, «почти все» целые положительные числа больше 1 000 000 000 000. Используя эту терминологию, мы видим, что утверждение

lim an = a

эквивалентно следующему утверждению: если I есть любой интервал с центром в точке a, то почти все числа an лежат в этом интервале.

Не мешает мимоходом отметить, что нет необходимости предполагать, что все члены an последовательности непременно имеют различные значения. В частности, совершенно допустимо, чтобы несколько из них, или бесконечное число, или даже, наконец, все числа an были равны предельному значению a. Например, вполне законно рассматривать последовательность a1 = 0, a2 = 0, . . . , an = 0, . . ., и ее предел есть, конечно, 0.

Как уже указано, последовательность an с пределом a называется сходящейся. Последовательность, не имеющая предела, называется расходящейся.

1 Это утверждение не вполне точно. — Прим. ред. наст. изд.

322 ФУНКЦИИ И ПРЕДЕЛЫ гл. VI

3) Последовательность 1, 2, 3, 4, . . . , а также «колеблющиеся» последова-

не имеют пределов.

Если в последовательности an члены возрастают таким образом, что рано или поздно становятся больше любого наперед назначенного числа K, то принято говорить, что an стремится к бесконечности, и тогда пишут: lim an = ∞ или an → ∞. Например, n2 → ∞ и 2n → ∞. Эта терминология удобна, хотя и не вполне последовательна, так как символ ∞ не принято рассматривать как число. Последовательность, стремящаяся к бесконечности, считается расходящейся.

Начинающие часто впадают в ошибку, думая, что переход к пределу при n → ∞ может быть выполнен совершенно просто путем подстановки n = ∞ в выражение общего члена an. Например, n1 → 0 потому,

что ∞1 = 0. Но символ ∞ не является числом, и его употребление в

выражении ∞1 незаконно. Попытка представить себе предел последовательности как «последний» член последовательности an при n = ∞ не попадает в цель и затемняет правильное понимание существа дела.

2. Монотонные последовательности. В общем определении сходимости и предела на стр. 313 не содержится требований, так или иначе стесняющих характер приближения сходящейся последовательности a1, a2, a3, . . . к своему пределу a. Простейший тип приближения осуществляется так называемыми монотонными последовательностями, примером которых может служить следующая:

12 , 23 , 34 , . . . , n +n 1 , . . .

Каждый член этой последовательности больше предыдущего. Действительно,

Последовательность такого рода, в которой an+1 > an, называется монотонно возрастающей. Аналогично, последовательность, для которой

§ 2 ПРЕДЕЛЫ 323

вающей. Последовательности этих двух типов могут приближаться к своему пределу лишь с одной стороны: «слева» или «справа». В противоположность этому существуют последовательности колеблющиеся, например, −1, 12 , − 13 , 14 , . . . Эта последовательность приближается к

своему пределу 0 «с обеих сторон» (см. рис. 11, стр. 89).

Монотонные последовательности обладают особенно простыми свойствами. Такого рода последовательность может не иметь предела и возрастать неограниченно, подобно последовательности

1, 2, 3, 4, . . . ,

где an = n, или последовательности

2, 3, 5, 7, 11, 13, . . . ,

для которой an есть n-е простое число pn. В этом случае последовательность стремится к бесконечности. Но если члены монотонно возрастающей последовательности остаются ограниченными, т. е. если каждый член меньше некоторой верхней границы B, заранее известной, то интуитивно ясно, что последовательность должна стремиться к некоторому определенному пределу a, не превышающему числа B. Мы сформулируем это положение как принцип монотонных последовательностей: монотонно возрастающая последовательность, ограниченная сверху, сходится к некоторому пределу. (Аналогичное утверждение имеет место относительно монотонно убывающей последовательности, ограниченной снизу.) Замечательно то, что значение предела a не должно быть известным заранее; теорема утверждает, что при выполнении указанных условий предел существует. Конечно, эта теорема справедлива лишь при условии, что предварительно введены иррациональные числа, и в

противном случае не всегда бы оправдывалась: в самом деле, в главе II

√

мы видели, что каждое иррациональное число (например, 2) является пределом монотонно возрастающей и ограниченной последовательности рациональных десятичных дробей, возникающих при обрывании некоторой бесконечной десятичной дроби на n-й цифре.

* Хотя принцип монотонных последовательностей интуитивно вполне очевиден и выглядит как абсолютная истина, однако не мешает, и даже весьма полезно, привести его вполне строгое доказательство в современном стиле. Чтобы это сделать, надо показать, что этот принцип есть логический вывод из определения действительного числа и определения предела.

Предположим, что числа a1, a2, a3, . . . образуют монотонно возрастающую, но ограниченную последовательность. Мы можем представить члены этой последовательности как бесконечные десятичные дроби

a1 = A1,p1p2p3 . . .

a2 = A2,q1q2q3 . . .

a3 = A3,r1r2r3 . . .

. . . . . . . . . . . . .

где Ai — целые числа, а pi, qi, ri и т. д. — цифры от 0 до 9. Пробежим теперь вниз по столбцу целых чисел A1, A2, A3, . . . Так как последовательность a1, a2, a3, . . . ограниченна, то эти целые числа не могут возрастать бесконечно, а поскольку она монотонно возрастает, то целые числа последовательности A1, A2, A3, . . . после достижения некоторого максимального значения должны стать постоянными. Обозначим это максимальное значение символом A и предположим, что оно достигнуто в N0-й строке. Станем теперь пробегать второй столбец p1, q1, r1, . . ., сосредоточивая свое внимание на членах N0-й и последующих строк. Если x1 есть наибольшая из цифр, появившаяся в этом столбце после N0-й строки, то эта цифра будет появляться всегда после своего первого появления, которое, предположим, произошло в N1-й строке, где N1 > N0. (Если бы цифра в этом столбце уменьшилась когдалибо впоследствии, то последовательность a0, a1, a2, . . . не была бы монотонно возрастающей.) Затем мы рассмотрим цифры p2, q2, r2, . . . третьего столбца. Рассуждение, подобное предыдущему, показывает, что начиная с некоторого целого числа N2 > N1 цифры третьего столбца постоянно равны некоторому числу x2. Если мы повторим этот процесс для 4-го, 5-го, . . . столбцов, то получим цифры x3, x4, x5, . . . и соответствующие целые числа N3, N4, N5, . . .

Легко убедиться, что число

a = A1,x1x2x3x4 . . .

есть предел последовательности a1, a2, a3, . . . В самом деле, пусть выбрано e > > 10−m; тогда для всех n > Nm целая часть и первые m цифр после запятой в числах an и a будут совпадать между собой, так что разность |an − a| не может превышать 10−m. Так как это можно сделать для любого e, как бы мало оно ни было, с помощью выбора достаточно большого m, то теорема доказана.

Эту теорему можно также доказать, основываясь на любом из данных в главе II определений действительного числа, например, взяв определение с помощью вложенных интервалов или дедекиндовых сечений. Такие доказательства можно найти в любом курсе анализа.

Принцип монотонных последовательностей мог бы быть применен в главе II при определении суммы и произведения двух положительных бесконеч-

ных десятичных дробей:

a = A,a1a2a3 . . .

b = B,b1b2b3 . . .

Два таких выражения не могут быть ни сложены, ни перемножены обычным путем, начиная с правого конца, поскольку нет никакого правого конца. (В качестве примера читатель может попытаться сложить следующие две бесконечные десятичные дроби: 0,333333 . . . и 0,989898 . . ..) Но если символ xn

обозначает конечную десятичную дробь, полученную в результате сложения конечных десятичных дробей, возникающих при «обрывании» на n-й цифре десятичных разложений a и b, то последовательность x1, x2, x3, . . . будет монотонно возрастающей и ограниченной (границей может служить, например, число A + B + 2). Отсюда следует, что последовательность x1, x2, x3, . . . имеет предел, и мы можем принять следующее определение:

a + b = lim xn.

Посредством подобного же процесса можно определить и произведение ab. Определения эти можно распространить и на все случаи, когда a и b — какие угодно положительные или отрицательные числа, применяя обычные правила арифметики.

Упражнение. Докажите, что суммой двух вышеуказанных бесконечных десятичных дробей является действительное число

1,323232 . . . = 13199 .

Важность понятия предела в математике заключается в том, что

многие числа могут быть определены лишь как пределы (часто как пределы монотонно возрастающих последовательностей). Вот почему поле рациональных чисел, в котором такие пределы могут не существовать, слишком узко для надобностей математики.

3. Число Эйлера e. Число e заняло видное место в математике рядом с архимедовым числом p сразу после опубликования Эйлером в 1748 г. сочинения «Introductio in Analysin Infinitorum». Это число является прекрасной иллюстрацией того, как принцип монотонных последовательностей может служить для определения нового действительного числа. Пользуясь обычной сокращенной записью для произведения n первых целых чисел

n! = 1 · 2 · 3 · . . . · n,

рассмотрим последовательность a1, a2, a3, . . ., где

Члены последовательности an монотонно возрастают, поскольку an+1 получается из an посредством прибавления положительного слагаемо-

1

го (n + 1)! . Кроме того, значения an ограничены сверху:

326 ФУНКЦИИ И ПРЕДЕЛЫ гл. VI

причем мы использовали формулу стр. 85 для суммы n первых членов геометрической прогрессии. Но в таком случае в силу принципа монотонных последовательностей an должно стремиться к некоторому пределу при стремлении n к бесконечности; этот предел обозначается буквой e. Чтобы выразить тот факт, что e = lim an, мы можем записать e в виде «бесконечного ряда»

Это «тождество» с рядом точек на конце есть просто другой способ для выражения двух следующих утверждений:

Ряд (6) позволяет вычислить e с любой степенью точности. Напри-

мер, сумма (с девятью цифрами) членов ряда (6) до 12!1 включительно равна числу

X

= 2,71828182 . . .

(Проверьте!) «Ошибка», т. е. разность между этим приближенным и истинным значением e, может быть легко оценена. Для разности e − P мы имеем выражение

Это число так мало, что не может повлиять на девятую цифру, и потому, допуская возможную ошибку в последней цифре вышеприведенного значения, мы получаем для e следующее приближенное равенство с восемью верными цифрами:

e ≈ 2,7182818.

Число e иррационально. Чтобы это доказать, предположим противное: допуская, что e = pq , где p и q — целые числа, и затем, приходя к противо-

речию, мы должны будем заключить о нелепости сделанного предположения. Поскольку мы знаем, что 2 < e < 3, e не может быть целым числом, а потому q по меньшей мере должно быть равно 2. Умножим обе части тождества (6)

на q! = 1 · 2 · 3 · . . . · q; получим

e · q! = p · 2 · 3 · . . . · (q − 1) =

=[q! + q! + 3 · 4 · . . . · q + 4 · 5 · . . . · q + . . . + (q − 1)q + q + 1] +

1 1

+q + 1 + (q + 1)(q + 2) + . . . (7)

Влевой части мы, очевидно, имеем целое число. В правой части слагаемое в квадратных скобках также есть целое число. Остаток же в правой

части есть положительное число, меньшее 12 , и значит, не есть целое число.

целое число в левой части не может быть равно числу в правой части, так как это последнее, являясь суммой целого числа и положительного числа, меньшего 12 , не есть целое число.

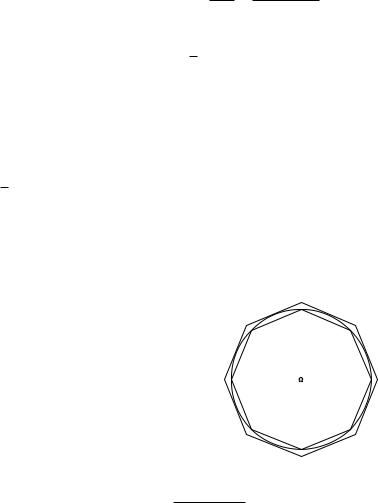
4. Число p. Как известно из школьной математики, длина окружности, радиус которой равен единице, может быть определена как предел последовательности длин периметров правильных многоугольников при бесконечном увеличении числа их сторон. Определенная таким образом длина

окружности обозначается символом 2p. Точнее, если через pn обозначить длину вписанного, а через qn длину описанного правильного n-угольника, то имеют место неравенства

pn < 2p < qn.

Более того, когда n возрастает, обе последовательности pn и qn приближаются монотонно к 2p, и на каждом этапе мы получаем все меньшую ошибку в том приближении,

содержащее m − 1 перекрывающихся квадратных корней. Эту формулу можно использовать для подсчета приближенного значения числа 2p.

Упражнения. 1) Найдите приближенное значение p, даваемое числами p4, p8 и p16.

*2) Найдите формулу для q2m.

*3) С помощью этой формулы вычислите q4, q8 и q16. Зная величины p16 и q16, установите границы, между которыми должно лежать число p.

Что же это за число p? Неравенство pn < 2p < qn дает на это полный ответ при развертывании последовательности вложенных интервалов, которые стягиваются к точке 2p. И все же этот ответ оставляет желать еще чего-то, поскольку он ничего не говорит о природе p как действительного числа: является ли оно рациональным или иррациональным, алгебраическим или трансцендентным? Как мы уже указывали на стр. 127, число p есть число трансцендентное, а следовательно, и иррациональное. В противоположность доказательству для e доказательство иррациональности p, впервые данное Ламбертом (1728–1777), в достаточной мере трудно и здесь приведено не будет. Однако ряд сведений о числе p мы можем сообщить. Имея в виду, что целые числа являются существенной основой математики, мы можем задать вопрос: связывается ли число p сколько-нибудь просто и непосредственно с целыми числами? Десятичное разложение числа p, хотя и вычисленное с несколькими сотнями знаков, не обнаруживает ни малейшей закономерности. Это и не удивительно: ведь p и число 10 не имеют между собой ничего общего. Однако Эйлер (XVIII в.) и другие нашли изящные выражения, связывающие число p с целыми числами с помощью бесконечных рядов и произведений. Простейшей из таких формул является, вероятно, следующая:

выражающая p

4

sn = 1 − 13 + 15 − . . . + (−1)n 2n1+ 1 .

Эту формулу мы выведем в главе VIII. Вот другой бесконечный ряд, который может служить для вычисления p:

И еще одно удивительное выражение для p было открыто английским математиком Джоном Уоллисом (1616–1703). Его формула утверждает следующее:

В сокращенном виде она часто записывается так:

p2 = 21 · 23 · 43 · 45 · 65 · 67 · 87 · 89 . . .

(выражения, подобные стоящему в правой части, называются бесконечными произведениями).

Доказательство последних двух формул можно найти в любом достаточно полном курсе анализа.