
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель
§ 6 |
ЕЩЕ ОБ ИНВЕРСИИ И ЕЕ ПРИМЕНЕНИЯХ |
185 |
некоторого круга с центром O. При движении механизма точка P описывает окружность с центром S, проходящую через O; значит, обратная точка Q описывает прямую линию.
Можно построить — по крайней мере теоретически — другие шарнирные механизмы, которые будут чертить эллипсы, гиперболы и даже любую наперед заданную алгебраическую кривую f(x, y) = 0, какова бы ни была ее степень.
§6. Еще об инверсии и ее применениях
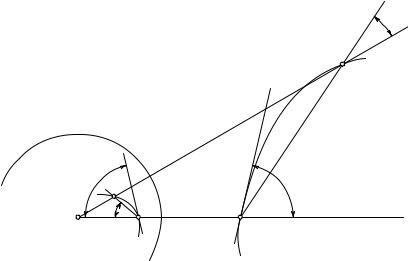
1.Инвариантность углов. Семейства окружностей. Хотя круговая инверсия есть преобразование, довольно резко меняющее внешний вид геометрических фигур, все же весьма замечательным является то обстоятельство, что вновь получаемые фигуры сохраняют некоторые свойства первоначальных фигур. Эти свойства, не теряющиеся при преобразовании, называются инвариантными. Мы уже знаем, что при инверсии окружность или прямая переходит в окружность или прямую. Прибавим теперь еще одно важное свойство инверсии: угол между двумя прямыми или кривыми при инверсии не изменяется. Говоря подробнее, это означает, что инверсия преобразовывает две пересекающиеся кривые в две другие кривые, которые пересекаются под тем же углом. Под углом между кривыми подразумевается угол между их касательными.
y
A
|
x0 |
A |
y0 |
|
|
|
|
|
|
|
|
x |
|
L |
O |
|
P |
P |
|
|
|
|||
|
|
C |
C |
|
|
|
|
|
|
Рис. 60. Инвариантность углов при инверсии |
|
|||
Доказательство получается при рассмотрении рис. 60, где имеется

186 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ гл. III
в виду частный случай пересечения в точке P произвольной кривой C с прямолинейным отрезком OL, проведенным из центра инверсии O. Кривая C0, обратная кривой C, пересекается с OL в точке P 0, обратной P , так как P 0, так же как и P , лежит на OL. Покажем, что угол x0 между OL и касательной к C в точке P по величине равен углу y0 между OL и касательной к C0 в точке P 0. Для этого возьмем точку A на кривой C вблизи P и проведем секущую AP .
Точка, обратная A, есть A0; так как она находится на прямой OA и на кривой C0, то является их точкой пересечения. Проведем также секущую A0P 0. По определению инверсии, r2 = OP · OP 0 = OA · OA0, или же
т. е. треугольники OAP и OA0P 0 подобны. Значит, угол x равен углу OA0P 0, который мы обозначим через y. Последний шаг в нашем рассуждении заключается в том, чтобы заставить точку A приближаться по кривой C к точке P . При этом секущая AP переходит в касательную к кривой C в точке P , и угол x стремится к x0. В то же время A0 будет приближаться к P 0 и прямая A0P 0 перейдет в касательную к кривой C0 в точке P 0, а угол y будет стремиться к y0. Так как при всяком положении точки A мы имеем равенство x = y, то оно сохранится и в пределе x0 = y0.
Наше доказательство еще не закончено, так как мы рассмотрели пока только случай пересечения кривой C с прямой, проходящей через центр O. Но рассмотреть общий случай пересечения двух произвольных кривых C и C теперь уже совсем легко. Пусть эти кривые пересекаются в точке P и образуют между собой угол z. Тогда прямая OP P 0 делит этот угол на два угла, из которых каждый в отдельности не изменяется при инверсии.
Следовало бы оговорить, что, хотя инверсия не изменяет величины угла, она, однако, изменяет направление его отсчета: если вообразим, что при постоянном увеличении угла x0 одна сторона его неподвижна, а другая вращается против часовой стрелки, то подвижная сторона соответствующего «обратного» угла вращается по часовой стрелке.
Частным следствием инвариантности углов при инверсии является то, что две ортогональные (т. е. пересекающиеся под прямым углом) окружности или прямые после инверсии сохраняют это свойство, и если две окружности взаимно касаются («пересекаются под углом, равным нулю»), то касаются и обратные им окружности.
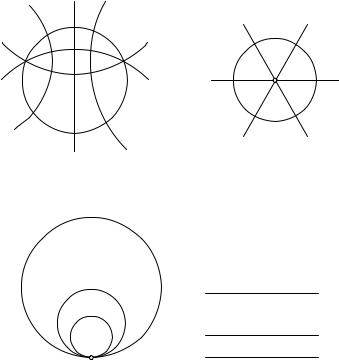
Рассмотрим семейство окружностей, проходящих через центр инверсии O и еще через одну и ту же неподвижную точку плоскости A. Мы знаем (§ 4, пункт 2), что это семейство преобразуется в семейство прямых, проходящих через точку A0, являющуюся образом A. В то же время семейство окружностей, ортогональных первоначальному семейству,
§ 6 |
ЕЩЕ ОБ ИНВЕРСИИ И ЕЕ ПРИМЕНЕНИЯХ |
187 |
превращается в семейство окружностей, ортогональных упомянутому семейству прямых. (На рис. 61 ортогональные семейства изображены пунктиром.) Внешне семейство прямых, проходящих через одну и ту же точку, мало напоминает семейство окружностей, но эти семейства связаны теснейшим образом — с точки зрения теории инверсии они, так сказать, вполне эквивалентны.
Вот другой пример того, к каким результатам приводит инверсия. Пусть дано семейство окружностей, проходящих через центр инверсии и имеющих в этой точке общую касательную. После инверсии получается семейство параллельных прямых. Действительно, так как окружности проходят через O, то они превращаются в прямые, и так как окружности не имеют точек пересечения кроме O, то получаемые прямые параллельны.
O 
 A
A
A
Рис. 61. Преобразование двух систем ортогональных окружностей с помощью инверсии
C
C
B
A B
A
Рис. 62. Преобразование касающихся окружностей в параллельные прямые
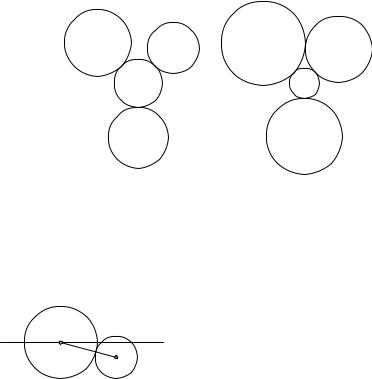
2. Применение к проблеме Аполлония. Прекрасной иллюстрацией того, насколько полезна теория инверсии, является следующее простое геометрическое решение проблемы Аполлония. При инверсии отно-
188 |
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ |
гл. III |
сительно какого бы то ни было центра проблема Аполлония для трех данных окружностей трансформируется в соответствующую проблему для трех других окружностей: пусть читатель внимательно продумает, почему это так.
Отсюда легко понять, что если проблема решена для некоторой тройки окружностей, то тем самым ее можно считать решенной и для всякой тройки окружностей, которая из первой тройки может быть получена путем инверсии. Мы сумеем использовать это обстоятельство, выбирая из всевозможных «эквивалентных» троек такую, для которой проблема решается особенно просто.
B  C
C  B
B  K C
K C 
O  O
O 
U
A  A
A 
Рис. 63. Подготовка построения, решающего проблему Аполлония
Предположим для определенности, что три данные окружности с центрами A, B, C взаимно не пересекаются и лежат каждая вне двух других, и допустим, что речь идет о нахождении окружности U с цент-
ром O и радиусом r, касающейся трех данных окружностей внешним |
|||||
|
|
|
|
образом. Заметим, что если мы увеличим |
|
|
b |
|
|
радиус всех трех данных окружностей на |
|
|
|
|
|
одну и ту же величину d, то окружность |
|
|
u |
|
|
||
|
|
a |
с центром O и радиусом r − d, очевид- |
||
|
O r |
A |
но, был бы решением видоизмененной та- |
||
|
s |
ким образом проблемы. Пользуясь этим |
|||
|
|
|
|
||
|
|
|
|
обстоятельством, увеличим радиусы дан- |
|
|
c |
|
|
||
Рис. 64. Решение |
проблемы |
ных окружностей на такую величину, что- |
|||
бы две из трех окружностей оказались |
|||||
|
|
|
|
||
Аполлония
взаимно касающимися в некоторой точке, которую обозначим K (рис. 63). Затем произведем инверсию всей фигуры относительно какой-нибудь окруж-
ности с центром K. Окружности с центрами B и C станут параллельными прямыми b и c, а третья окружность превратится в некоторую окружность a (рис. 64). Мы уже знаем, что a, b, c могут

§ 6 |
ЕЩЕ ОБ ИНВЕРСИИ И ЕЕ ПРИМЕНЕНИЯХ |
189 |
быть построены с помощью циркуля и линейки. Что касается искомой окружности U, то она преобразуется в окружность u, касающуюся прямых b, c и окружности a. Ее радиус r, очевидно, должен равняться половине расстояния между прямыми b и c; центр же ее O0 должен совпадать с одной из точек пересе-
чения средней линии между b и c с окружностью, концентрической окружности a, но имеющей радиус на r больший. Остается применить обратную инверсию к окружности u, и тогда получим искомую аполлониеву окружность U.
3. Повторные отражения. Каждому |
|
|
|
из нас приходилось наблюдать странные яв- |
|
|
|
ления отражения, возникающие, если имеет- |
Рис. 65. Повторное отра- |
||
ся более одного зеркала. Если четыре стены |
|||
прямоугольной комнаты представляют собой |
жение относительно пря- |
||
идеальные зеркала, ни в малой степени не |
молинейных стен |
||
поглощающие света, то находящаяся в этой комнате освещенная точка создает бесконеч-
ное множество отражений, по одному на каждую из прямоугольных комнат, возникающих из первой посредством отражений (рис. 65). При менее правильной форме соединения зеркал, например при трех зеркалах, создается более сложная система отражений. Получающуюся
Рис. 66. Правильные системы треугольных зеркал
конфигурацию легко описать только в том случае, если отраженные треугольники, не перекрывая друг друга, полностью покрывают плоскость. Таким свойством обладают только прямоугольный равнобедренный треугольник, равносторонний треугольник и прямоугольный треугольник, представляющий собою половину равностороннего (рис. 66).
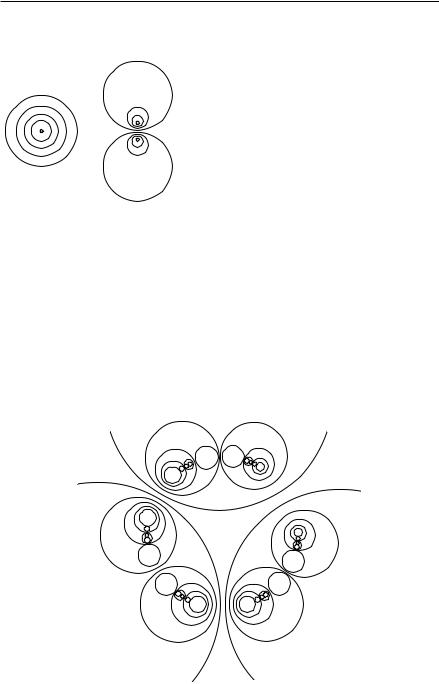
Еще более курьезные обстоятельства возникают, если мы станем рассматривать повторные инверсии относительно пары окружностей. Поместившись между двумя концентрическими сферическими зер-
190 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ гл. III
калами, мы увидали бы бесчисленное множество концентрических отражений. Одна последовательность отражений уходила бы в бесконечность, другая — сосредоточивалась бы около центра. Случай двух окружностей, расположенных одна вне другой, несколь-
ко сложнее: окружности и их отражения последовательно отражаются одна в другой, уменьшаясь после каждого отражения и теснясь к двум предельным точкам, по одной в каждой из данных окружностей. (Эти точки обладают
Рис. 67. Повторное отраже- |
свойством взаимной обратности относи- |
|||
ние относительно двух сфери- |
||||
тельно каждой из данных окружностей.) |
||||
ческих дуг |
||||
Все это показано на рис. 67. Что по- |
||||
|
|
|||
|
|
лучится в случае трех кругов, об этом |
||
|
|
читатель может составить впечатление, |
||
взглянув на узор, изображенный на рис. 68. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 68. Отражение относительно трех сферических зеркал
