
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель
§ 4 |
ТРЕУГОЛЬНИК ШВАРЦА |
375 |
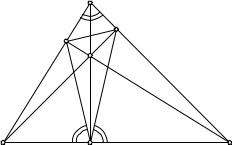
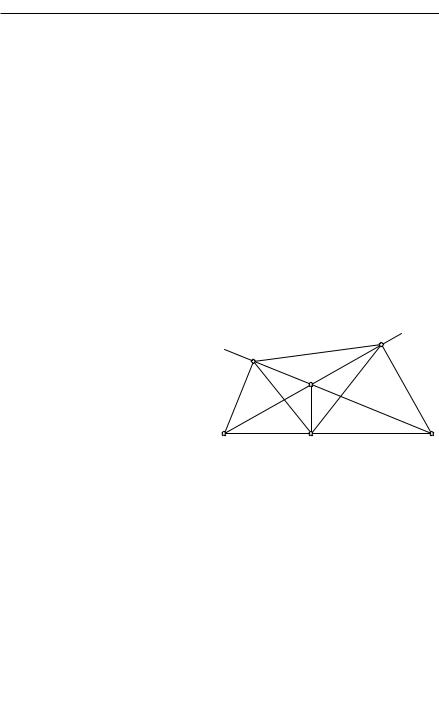
§4. Треугольник Шварца
1.Доказательство, предложенное Шварцем. Герман Амандус Шварц (1843–1921), выдающийся математик, профессор Берлинского университета, сделал многое для развития современной теории функций
ианализа. Он не считал ниже своего достоинства писать на темы элементарного содержания, и одна из его работ посвящена следующей задаче: в данный остроугольный треугольник вписать другой треугольник с минимальным периметром. (Говоря, что некоторый треугольник вписан в данный, мы подразумеваем, что на каждой из сторон данного треугольника имеется вершина рассматриваемого треугольника.) Мы убедимся в дальнейшем, что существует только один искомый треугольник: именно, его вершинами являются основания высот данного треугольника. Такой треугольник условимся называть высотным треугольником.
Шварц доказал минимальное свойство высотного треугольника, применяя метод отражения и основываясь на следующей теореме элементарной геометрии: в каждой из вершин P , Q, R (рис. 197) две стороны высотного треугольника образуют одинаковые углы со стороной данного треугольника, именно, каждый из этих углов равен углу при противоположной вершине данного треугольника. Например, углы ARQ
иBRP равны каждый углу C и т. д.
C
P
Q
O
A R B
Рис. 197. Высотный треугольник в треугольнике ABC
Докажем прежде всего эту теорему. Так как углы OP B и ORB прямые, то около четырехугольника OP BR можно описать окружность. Следовательно, P BO = P RO, так как названные углы опираются на одну и ту же дугу описанной окружности. Но угол P BO дополнительный к углу C, так как треугольник CBQ прямоугольный, а угол P RO дополнительный к углу P RB. Поэтому P RB = C. Таким же образом, рассуждая по поводу четырехугольника QORA, заключаем, что QRA = C и т. д.
376 МАКСИМУМЫ И МИНИМУМЫ гл. VII
Этот результат приводит к следствию, относящемуся к высотному треугольнику: так как, например, AQR = CQP , то при отражении относительно стороны AC данного треугольника сторона RQ направ-
ляется по стороне P Q, и |
|
|
|||
обратно. Аналогично для |
|
|
|||
других сторон. |
|
|
|
||
Перейдем теперь к до- |
|
B |
|||
казательству |
минималь- |
|
P |
||
|
|
||||
ного свойства |
высотно- |
|
U |
||
го треугольника. В тре- |
|
|
|||
угольнике ABC рассмот- |
|
|
|||
рим, наряду с высотным |
C |
A |
|||
треугольником, |
какой- |
|
|
||
нибудь другой |
|
|
|
|
|
вписанный треугольник, |
скажем, |
|
|||
UV W . Отразим всю фигуру снача- |
|
||||
ла относительно стороны AC тре- |
B |
||||
угольника ABC, затем вновь по- |
|
||||
лучившуюся фигуру отразим от- |
C |
||||
носительно стороны AB, потом — |
|||||
|
|||||
относительно |
BC, потом — отно- |
|
|||
сительно AC и, наконец, относи- |
A |
||||
тельно AB. Таким образом мы по- |
|
||||
лучим всего шесть конгруэнтных |
|
||||
треугольников, причем в каждом |
|
||||
из них будет заключен высотный |
B |
||||
треугольник и еще другой вписан- |
P |
||||
ный треугольник (рис. 198). Сто- |
U |
||||
рона BC последнего треугольника |
|||||
|
|||||
параллельна стороне BC первого |
|
||||
треугольника. В самом деле, при |
C |
||||
первом отражении сторона BC по- |
Рис. 198. Доказательство минималь- |
||||
ворачивается |
по |
часовой |
стрелке |
||
на угол 2C, затем опять по часовой
стрелке на угол 2B; при третьем отражении — остается неизменной;
при четвертом — поворачивается на угол 2C против часовой стрелки и при пятом — на угол 2B опять против часовой стрелки. Итого, общий угол поворота равен нулю.
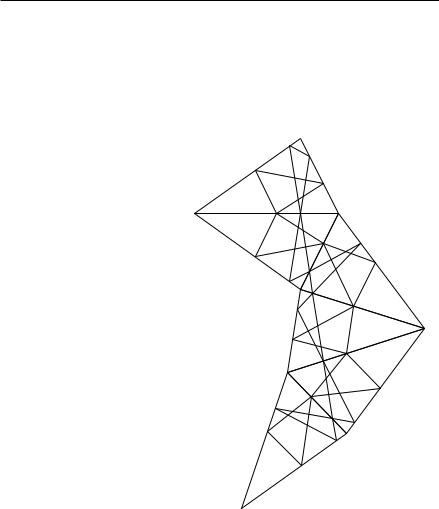
Благодаря указанному выше свойству высотного треугольника прямолинейный отрезок P P 0 равен удвоенному периметру треугольника P QR: действительно, P P 0 составляется из шести отрезков, по очереди равных первой, второй и третьей стороне P QR, причем каждая из
§ 4 ТРЕУГОЛЬНИК ШВАРЦА 377
сторон входит дважды. Таким же образом ломаная линия, соединяющая U и U0, имеет длину, равную удвоенному периметру треугольника UV W . Эта ломаная не короче, чем прямолинейный отрезок UU0. Что же касается прямолинейного отрезка UU0, то он равен P P 0, так
как отрезок UU0 параллелен |
P P 0. Значит, ломаная линия UU0 |
не |
короче, чем прямая P P 0, т. е. |
периметр высотного треугольника |
не |
больше, чем периметр любого другого треугольника, вписанного в данный. Это и нужно было доказать. Итак, установлено, что минимум существует и что он реализуется в случае высотного треугольника. Что нет иного вписанного треугольника с тем же периметром — это, однако, не доказано, и это мы докажем дальше.
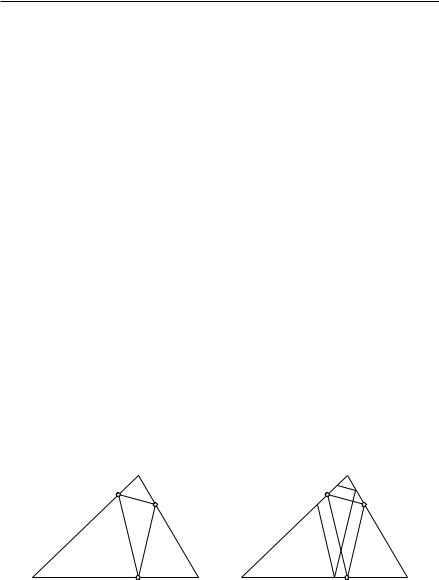
2. Другое доказательство. Следующее решение задачи Шварца является, вероятно, самым простым. Оно основывается на теореме, ранее доказанной в этой главе: если точки P и Q лежат по одну сторону прямой L (но не на ней самой), то сумма расстояний P R + RQ, где R — точка на L, обращается в минимум в том случае, если P R и QR образуют одинаковые углы с L. Пусть треугольник P QR, вписанный в данный треугольник ABC, решает поставленную минимальную задачу. Тогда точка R на стороне AB должна быть такой, чтобы сумма P R + QR была наименьшей, следовательно, углы ARQ и BRP должны быть равны; и точно так же AQR = CQP , BP R = CP Q. Таким образом, для искомого треугольника с минимальным периметром — если только таковой существует — должно быть выполнено то же самое свойство равенства углов, каким обладает высотный треугольник. Остается показать, что при таком условии наш треугольник не может отличаться от высотного. Кроме того, так как в теореме, на которую мы ссылались,
|
C |
|
C |
Q |
r |
|
Q |
|
P |
P |
|
|
|
pq
A R B A R B
Рис. 199–200. Другое доказательство минимального свойства высотного треугольника
предполагается, что P и Q не лежат на AB, то доказательство не годится для случая, когда одна из точек P , Q, R совпадает с какой-нибудь вершиной данного треугольника (при этом периметр треугольника выродился бы в удвоенную соответствующую высоту); чтобы доказательство
378 |
МАКСИМУМЫ И МИНИМУМЫ |
|
|
|
гл. VII |
|||
было исчерпывающим, нужно еще установить, что периметр высотного |
||||||||
треугольника меньше любой из удвоенных высот данного треугольника. |
||||||||
Обращаясь сначала к первому пункту, заметим, что если впи- |
||||||||
санный треугольник обладает указанным выше свойством равенства |
||||||||
углов, то рассматриваемые углы при вершинах P , Q и R соответствен- |
||||||||
но равны углам A, B и C. В самом деле, допустим, например, что |
||||||||
ARQ = BRP = C + d. Тогда, |
применяя теорему о сумме углов |
|||||||
треугольника к треугольникам ARQ и BRP , мы видим, что углы при Q |
||||||||
должны равняться B − d, а углы при P должны равняться A − d. |
||||||||
Но тогда сумма углов треугольника CP Q равна (A − d) + (B − d) + |
||||||||
C = 180◦ − 2d; с другой стороны, она же равна 180◦. Поэтому d = 0. |
||||||||
Мы уже видели, что высотный треугольник обладает отмеченным |
||||||||
свойством. Всякий иной вписанный треугольник, обладающий тем же |
||||||||
свойством, имел бы стороны, соответственно параллельные сторонам |
||||||||
высотного |
треугольника; |
другими |
словами, он был бы ему подобен |
|||||
|
|
|
и подобно расположен. Чита- |
|||||
|
C |
|
тель |
докажет |
самостоятельно, |
|||
|
|
|
что, |
кроме |
самого |
высотного |
||
|
|
|
треугольника, |
|
другого |
такого |
||
Q |
P |
L |
треугольника |
|
не |
существует |
||
(рис. 200). |
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
Покажем, наконец, по-преж- |
|||||
|
|
|
нему ограничиваясь случаем ост- |
|||||
|
N |
|
роугольного |
треугольника, что |
||||
|
|
B |
периметр высотного треугольни- |
|||||
|
R |
|
ка меньше, чем любая удвоен- |
|||||
A |
M |
|
ная высота данного треугольни- |
|||||
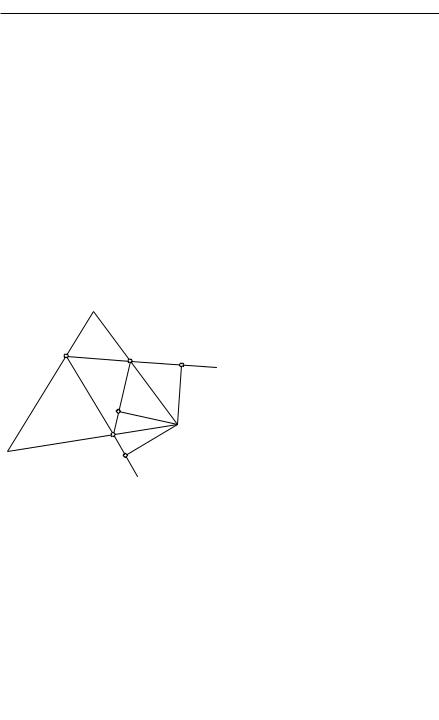
|
|
|
ка. Проведем прямые QP и QR |
|||||
Рис. 201. К доказательству минималь- |
и затем из вершины B (рис. 201) |
|||||||
ного свойства высотного треугольника |
опустим перпендикуляры на пря- |
|||||||
|
|
|
мые QP , QR и P R; пусть L, M |
|||||
и N — основания этих перпендикуляров. Так как отрезки QL и QM |
||||||||
являются проекциями высоты QB на прямые QP и QR, то QL + QM < |
||||||||
< 2QB. Но QL + QM = p, где через p обозначен периметр высотного |
||||||||
треугольника. Действительно, треугольники MRB и NRB равны, так |
||||||||
как MRB = NRB, а углы при вершинах M и N прямые. Значит, |
||||||||
RM = RN; и поэтому QM = QR + RN. Точно так же мы убеждаемся, |
||||||||
что P N = P L и, следовательно, QL = QP + P N. Отсюда вытекает: |
||||||||
QL + QM = QP + P N + QR + RN = QP + P R + RQ = p. Но раньше |
||||||||
было показано, что 2QB > QL + QM. Итак, p меньше, чем удвоенная |
||||||||
высота QB. Это же рассуждение может быть применено и к каждой |
||||||||
из двух других высот. Таким образом, минимальное свойство высотного |
||||||||
треугольника доказано полностью. |
|
|
|
|
|
|
||
§ 4 |
ТРЕУГОЛЬНИК ШВАРЦА |
|
379 |
||
Между прочим, приведенное построение позволяет непосредственно вы- |
|||||
числить p. Мы знаем, что углы P QC и RQA равны углу B, так что P QB = |
|||||
RQB = 90◦ − B и cos P QB = sin B. Отсюда следует, с помощью элемен- |
|||||
тарных тригонометрических соображений, что QM = QL = QB sin B, и p = |
|||||
2QB sin B. Таким же образом можно показать, что p = 2P A sin A = 2RC sin C. |
|||||
Из тригонометрии известно, что RC = a sin B = b sin A и т. д., откуда следу- |
|||||
ет: p = 2a sin B sin C = 2b sin C sin A = 2c sin A sin B. И наконец, вводя радиус |
|||||
описанного круга r и принимая во внимание, что a = 2r sin A, b = 2r sin B, |
|||||
c = 2r sin C, мы получим симметрическую формулу |
|
|
|||
|
p = 4r sin A sin B sin C. |
|
|
||
3. Тупоугольные треугольники. В обоих предшествующих до- |
|||||
казательствах предполагалось, что все три угла A, B, C острые. Если бы, |
|||||
скажем, угол C был тупой (рис. 202), то точки P и Q лежали бы вне тре- |
|||||
угольника. Поэтому, строго говоря, высотный треугольник уже нельзя |
|||||
было бы считать вписанным в данный, если только мы не условимся за- |
|||||
ранее называть вписанным такой треугольник, вершины которого лежат |
|||||
на сторонах данного треугольника или на их продолжениях. Как бы то |
|||||
ни было, высотный треугольник |
|
|
|
||
в расширенном смысле не обла- |
|
|
Q |
||
дает минимальным периметром, |
P |
|
|
||
так |
как P R > CR, QR > CR, |
|
C |
|
|
и, значит, p = P R + QR + P Q > |
|
|
|||
|
|
|
|||
> 2CR. Так как рассуждение в |
|
|
|
||
первой части последнего доказа- |
|
|
|
||
тельства показывает, что мини- |
|
|
|
||
мальный периметр — если толь- |
A |
R |
B |
||
ко он не дается высотным тре- |
Рис. 202. Высотный треугольник в ту- |
||||
угольником — должен быть ра- |
|||||
поугольном треугольнике |
|||||
вен одной из удвоенных высот, |
|||||
|
|
|
|||
то отсюда легко заключить, что в случае тупоугольного треугольни- |
|||||
ка «вписанный треугольник» с наименьшим периметром есть не что |
|||||
иное, как высота, опущенная из вершины тупого угла, учитываемая в |
|||||
обоих направлениях; хотя треугольника в собственном смысле здесь и |
|||||
нет, однако можно все же указать настоящие вписанные треугольники, |
|||||
периметры которых как угодно мало отличаются от удвоенной высоты. |
|||||
В промежуточном случае, когда данный треугольник прямоугольный, |
|||||
оба решения (высотный треугольник и удвоенная высота, опущенная из |
|||||
прямого угла) совпадают. |
|
|
|
||
Не лишен интереса вопрос о том, не обладают ли каким-нибудь экс- |
|||||
тремальным свойством высотные треугольники данных тупоугольных |
|||||
треугольников. Не имея возможности подробно рассматривать этот во- |
|||||
прос, отметим лишь, что такие высотные треугольники не обращают |
|||||
в минимум сумму сторон p + q + r, но зато обеспечивают стационар- |
|||||
380 |
МАКСИМУМЫ И МИНИМУМЫ |
гл. VII |
ное значение типа минимакса для выражения вида p + q − r, где r — та сторона вписанного (в расширенном смысле) треугольника, которая соответствует тупому углу.
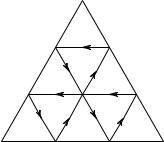
4. Треугольники, образованные световыми лучами. Если допустим, что треугольник ABC изображает комнату с зеркальными стенами, то высотный треугольник определяет единственный треугольный контур, который может быть образован световым лучом. Другие замкнутые многоугольные контуры также не исключены, как показывает рис. 203, но высотный тре-
угольник имеет три стороны.
Обобщим рассматриваемую проблему и спросим себя о возможных «световых треугольниках» в произвольной обла-
сти, ограниченной одной или несколькими гладкими кривыми; точнее говоря, нас интересуют треугольники, вершины которых лежат на заданных кривых, а каждые две прилежащие стороны образуют равные углы с соответствующей кривой. Мы
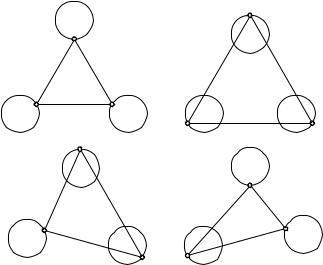
видели в § 1, что равенство углов является необходимым условием как для максимума, так и для минимума суммы соответствующих сторон, так что, смотря по обстоятельствам, могут возникать различные типы световых треугольников. Так, рассматривая внутренность единственной замкнутой гладкой кривой C, мы можем сказать, что вписанный треугольник максимального периметра должен быть «световым треугольником», обладающим вышеописанными свойствами. Или предположим еще, что каждая из вершин треугольника ABC имеет право находиться на ей соответствующей одной из трех замкнутых гладких кривых (идея Марстона Морса). Тогда световые треугольники характеризуются тем свойством, что их периметры имеют стационарные значения. Но такого рода значение может быть минимальным по отношению ко всем трем вершинам A, B, C; или может быть минимальным по отношению к двум каким-либо вершинам и максимальным по отношению к третьей, или минимальным по отношению к одной какой-нибудь из трех и максимальным относительно двух других; или, наконец, максимальным относительно всех трех. Всего, таким образом, существует по меньшей мере 23 = 8 типов световых треугольников, так как по отношению к каждой из вершин, и притом независимо, возможен максимум или минимум.
*5. Замечания, касающиеся задач на отражение и эргодическое движение. В динамике и в оптике представляется задачей первостепенной важности дать описание пути или «траектории» части-
§ 4 |
ТРЕУГОЛЬНИК ШВАРЦА |
381 |
цы или светового луча в пространстве на протяжении неограниченного промежутка времени. Предполагая, что то или иное приспособление физически принуждает частицу или луч оставаться в некоторой ограниченной части пространства, особенно интересно установить, заполняет ли траектория в пределе эту часть пространства повсюду с приблизительно одинаковой «плотностью». Траектория, обладающая таким свойством, называется эргодической. Допущение существования эргодической траектории является исходной гипотезой для применения статистических методов в современных динамических и атомных теориях. Но известно лишь очень немного ситуаций, при которых может быть проведено строгое математическое доказательство «эргодической гипотезы».
Рис. 204–207. Четыре типа световых треугольников между тремя кругами
Простейшие примеры относятся к случаю, когда движение происходит на плоскости внутри замкнутой кривой C, причем предполагается, что «стенка» C представляет собой математически совершенное зеркало, отражающее частицу (в остальном — свободную) под тем же углом, под каким она падает на стенку. Так, например, прямоугольный ящик — идеализированный бильярдный стол с совершенным отражением, причем рассматриваемая частица играет роль бильярдного шара, — обеспечивает, вообще говоря, эргодическое движение: идеальный «бильярдный шар» на протяжении бесконечного промежутка времени побывает в окрестности любой наперед заданной точки, если только исключить некоторые особые начальные положения и направления движения. Мы не приводим здесь доказательства, впрочем, не представляющего труд-
