Osnovy_teploperedachi_i_massoobmena_2015

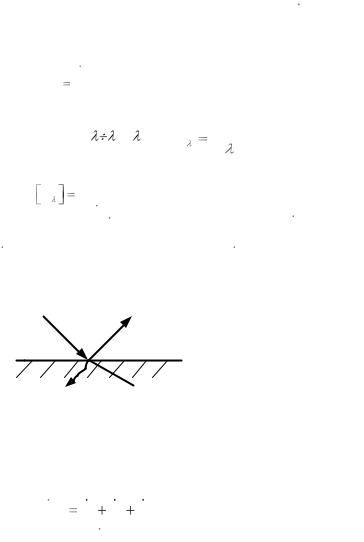
Основные положения теплового излучения

Полное количество энергии, излучаемое в единицу времени с

произвольной поверхности F (м2), называется потоком излучения Q

(Вт). Поток излучения с единицы поверхности по всем направлениям полусферического пространства

называется плотностью потока излучения тела. Если рассматривается

Q QR

QA QD

Рис. 1. Схема распределения падающего на тело теплового потока

Согласно закону сохранения энергии можно составить уравнение теплового баланса:

глощает весь падающий поток излучения – абсолютно черное тело

(R = 0 и D = 0);

кает весь падающий поток излучения – абсолютно прозрачное тело

(А = 0 и R = 0).

Основные законы излучения

Закон Планка. Устанавливает зависимость величины спектральной плотности потока излучения абсолютно черного тела Еоот

e Т 1

где С1 и С2 – постоянные Планка.

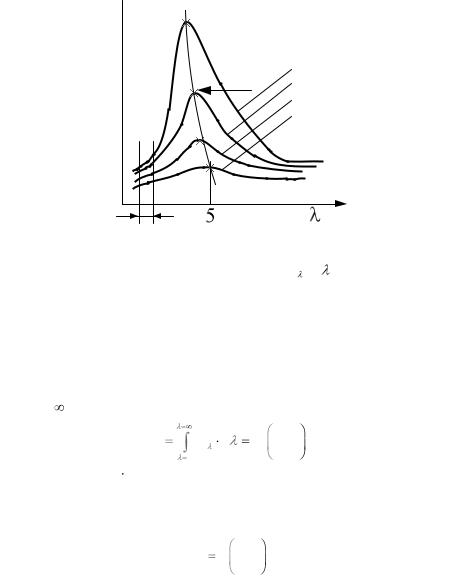
Из рис. 2, на котором закон Планка представлен графически, видно, что спектральная плотность потока излучения при отдельных температурах Т=const проходит через максимум. При =0 и = эта плотность стремится к нулю. С повышением температуры плотность потока излучения значительно увеличивается. Излучение существенно только в интервале длин волн от 0,8 до 400 мкм.

Закон Вина. С каждым последующим повышением температуры Т максимум спектральной плотности потока излучения абсолютного черного тела Ео смещается в сторону более коротких длин волн –

- 194 -

E0

1200 K

1000 K

800 K

600 K

, мкм

0,4 - 0,8 мкм

Рис. 2. График зависимости Ео =f( ,Т)

Произведение длины волны, при которой имеет место максимум спектральной плотности потока излучения абсолютно черного тела, на абсолютную температуру есть величина постоянная.

Закон Стефана-Больцмана. Устанавливает зависимость интегральной плотности потока излучения абсолютно черного тела Ео от температуры Т. Проинтегрировав Еопо всему интервалу длин волн (от 0 до ), получим

где Со = 5,67 Вт/(м2 К4) – коэффициент излучения абсолютного черного тела.

Закон Стефана-Больцмана выполняется и для реальных – серых – тел. В этом случае он принимает вид

где Е – интегральная плотность потока излучения серого тела; С – коэффициент излучения данного серого тела (С Со ), С изменяется в диапазоне 0 – 5,67.

- 195 -

Связь между плотностями потоков излучения данного тела и абсолютно черного тела при одной и той же температуре представляется в виде

где - интегральная степень черноты серого тела.

Знание величины степени черноты рассматриваемых серых тел позволяет рассчитать плотность потока излучения этих тел:

С учетом (6) уравнение (9) принимает вид

Абсолютно черное тело при данной температуре обладает наибольшей излучательной способностью по сравнению с другими телами. Поэтому степень черноты серых тел может принимать значения от 0 до 1.

Для реальных тел степень черноты является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности, а для металлов – от степени окисления этой поверхности. Для чистых металлов с полированной поверхностью при невысоких температурах 0,1. Степень черноты металлов растет с увеличением температуры практически линейно. Для чистых гладких металлов степень черноты связана с удельным электрическим сопротивлением эл зависимостью [1]

С появлением окисных пленок на поверхности металлов степень черноты может принимать значение мет=0,5 и выше. Степень черноты диэлектриков выше, чем чистых металлов, и обычно уменьшается с увеличением температуры. Степень черноты различных тел – это справочная характеристика, еѐ значения при различных условиях приводятся в литературе.

Описание экспериментальной установки и методика измерений

Существуют различные методы измерения степени черноты и коэффициента излучения тел. В каждом из них создаются условия, когда перенос тепла за счет конвекции и теплопроводности оказывается пренебрежимо малым по сравнению с излучением. Воспользуемся

- 196 -

методом, который можно считать калориметрическим, так как он основан на непосредственном измерении лучистого потока, испускаемого изучаемым телом.

Теплообмен излучением в замкнутой системе, состоящей из двух тел, описывается законом Стефана-Больцмана

где Qл - поток излучения, испускаемый поверхностью исследуемого

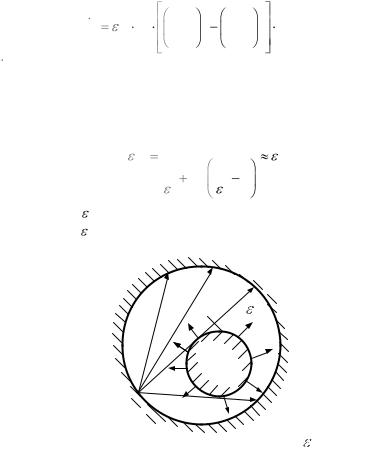
тела F1. Система состоит из нагреваемой электрическим током проволоки с поверхностью F1 и стеклянной оболочки с поверхностью F2. Приведенная степень черноты этих тел при условии, что F1<<F2 :

то есть величину пр в уравнении (12) можно принять равной искомой степени черноты 1 излучающего материала проволоки – нихрома или вольфрама.

1.F1,T1, 1

2.F2 ,T2 , 2

Рис. 3. Схема расположения двух излучающих тел

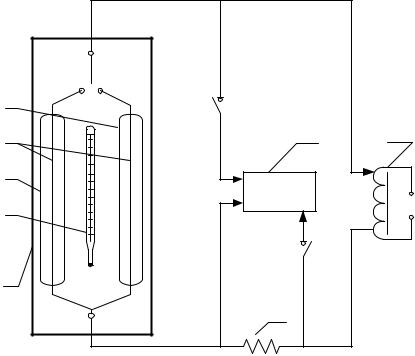
Основным элементом экспериментальной установки (рис. 4) является калориметр. Он выполнен в виде стеклянного вакууммированного баллона 1 с впаянной в него излучающей проволокой 5 с поверхностью F1. Стенки баллона являются тепловоспринимающими

- 197 -

поверхностями F2. Оба калориметра помещены в герметичный контейнер 7 из органического стекла.

Вакууммирование внутренней полости баллона до остаточного давления воздуха порядка 10-5 мм рт. ст. позволяет пренебречь переносом тепла конвекцией и теплопроводностью из-за отсутствия носителей этих видов переноса. Поэтому будем считать, что весь выделяемый тепловой поток Q от проволоки передается стенкам оболочки

только излучением. Этот тепловой поток определяется согласно закону Джоуля – Ленца по измеренным значениям напряжения Uэл и силы тока I, проходящего через проволоку.

Температуру излучающей поверхности проволоки Т1 устанавливают по измеренным значениям падения напряжения на проволоке, используя градуировочную зависимость Т1=f(Uэл) (прил. 1 и прил. 2). Температура внутренней поверхности стеклянного баллона t2 принимается равной температуре воздуха в контейнере 7 и измеряется ртутным термометром t2.

Проведение опытов

1.Подключить установку к электрической сети.

2.Переключатель П1 (переключатель тока, подаваемого на нихромовую или вольфрамовую нить) поставить в положение «НИХРОМ».

3.Переключатель П2 установить в положение «I» – ток. При помощи трансформатора (поз. 3 на рис. 4) установить значение силы

тока I1= I KI в соответствии с вариантом задания (показания цифрового прибора I умножаются на коэффициент КI = 0,01). Внести значения силы тока в таблицу измерений (табл. 2).

4. Переключатель П3 установить в положение Uэл – падение напряжения. (Показания цифрового прибора умножаются на коэффициент Кu = 0,01). Внести значения падения напряжения Uэл= u Кu в таблицу измерений (табл. 2).

5.Аналогично произвести измерения при токах I2 и I3 значений Uэл2 и Uэл3 ,внести их в таблицу измерений (табл. 2).

6.Переключатель П1 установить в положение «ВОЛЬФРАМ».

7.Произвести измерения в последовательности, соответствующей пунктам 3–5. Показания прибора внести в таблицу измерений (табл. 2).

8.Температура поглощающих поверхностей стеклянных колб

принимается равной температуре воздуха в контейнере, t2. За время опыта она практически не меняется; измеряется при помощи ртутного термометра 6, расположенного в контейнере 7.

9.Показать таблицу измерений преподавателю. Отключить установку от сети.

5

4

6

1 П1

3

а

- 199 -

б

Рис. 4. Стенд к лабораторной работе (а) и схема экспериментальной установки (б): 1 и 2 – вакуумированные стеклянные колбы калориметра с излучающим телом – нихромовой или вольфрамовой проволокой 5; 3 – источник питания - автотрансформатор; 4 – измерительный прибор – вольтамперметр; 6 – ртутный термометр; П2 и П3 – переключатели тока и напряжения, подаваемого на нити; 7 – контейнер, в котором размещены оба калориметра 1 и 2; П1 – переключатель, попеременно подводящий ток то к нихромовой, то к вольфрамовой нити, 8 – шунт для измерения тока

- 200 -

Обработка опытных данных

1.Определить температуру проволоки t1 (oC) по измеренным значениям показаний вольтметра Uэл из градуировочного графика (см. прил. 1–2). Рассчитать абсолютную температуру: Т1=t1 + 273, К.

2.Записать температуру стенки калориметра, принимая ее равной температуре воздуха в контейнере из органического стекла:

Т2=t2+273, К.

3.По измеренным в опыте значениям силы тока I и напряже-

Рассчитанные значения внести в табл. 3. и табл. 4.

4. Определить площади излучающих поверхностей нихромовой и вольфрамовой проволок, соответствующих каждой из измеренных температур, с учетом линейного расширения:

где для нихрома: lo = 0,45 м – длина проволоки при 0оС; d =0,00029 м – диаметр проволоки; 1 = 18,0 10-6 1/К – коэффициент линейного расширения; для вольфрама: lo = 0,45 м; d = 0,0003 м; 2 = 4,5 10-6 1/К.

5. Принимая, что при F1<<F2 приведенная степень черноты пр.1, учитывая уравнения (13), рассчитать из уравнения (12) степень черноты нихромовой и вольфрамовой проволок эксп = 1 при каждой из измеренных температур Т1. Результаты расчетов занести в табл. 3 и

табл. 4. (отдельно для нихрома и вольфрама).

6. По результатам обработки опытов построить график зависимости эксп=f(T1), выбрав масштаб по осям:

7.По уравнению (11) рассчитать степень черноты расч нихрома

ивольфрама при исследованных в опыте температурах. Величина удельного электрического сопротивления этих металлов определяется по формуле

эл о (1 ti ), (16)

где о – удельное электрическое сопротивление металла при t = 0o, Ом см; – температурный коэффициент сопротивления, 1/К. Для ни-

- 201 -

Такая же таблица расчетных величин составляется и для вольфрамовой проволоки.

- 202 -