клонными прямыми с точками А и В. Отрезки ОА и ОВ будут являться направлениями соответственно напряжений 1 и 2 .
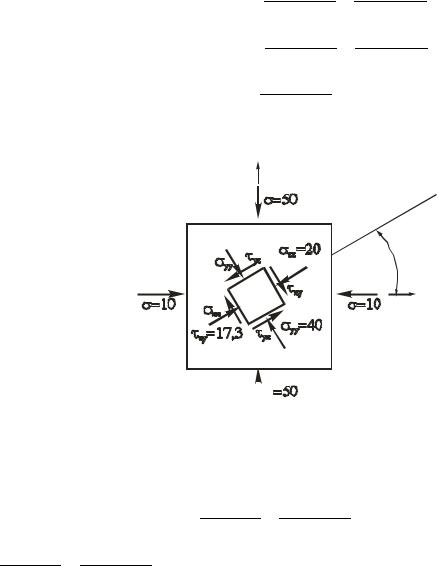
Пример 5.8. На главных площадках действуют напряжения 1 0;2 10МПа; 3 50МПа. Требуется определить величину напряжений на площадках, одна из которых составляет с напряжением 2 угол 30 .
Расчеты произвести аналитическим и графическим путем.
Решение
1. Вычисляем напряжения на наклонных площадках аналитически
xx 2 |
3 |
2 |
3 |
cos2 |
10 50 |
|
10 50 |
cos60 20МПа; |
|
2 |
|
2 |
|
2 |
|
2 |
|
yy 2 |
3 |
2 |
3 |
cos2 |
10 50 |
|
10 50 |
cos60 40МПа; |
|
2 |
|
2 |
|
2 |
|
2 |
|
|
xy |
2 |
3 |
sin 2 |
10 50 |
sin60 17,32МПа |
|
|
|
2 |
|
2 |
|
|
|
Учитывая знаки вычисленных напряжений, показываем их на гранях элемента (рис. 5.26).
3
 3
3
Рис. 5.26. Расчетная схема (к примеру 5.8)
2. Производим графический анализ напряженного состояния в точке. Учитывая знаки заданных главных напряжений откладываем по оси
их значения: отрезок ОА - 3 ; отрезок ОВ - 2 . Определяем координату центра
окружности |
ОО 2 |
3 |
10 50 30МПа |
и |
радиусом |
|
1 |
2 |
2 |
|
|
|
R 2 3 |
|
|
|
|
10 50 20МПа строим эту окружность. Из центра О под уг- |
2 |
2 |
|
|
|
1 |
|
|
|
|
|
|
лом 2 проводим луч до пересечения с окружностью и получаем точку |
Dx . |
Координаты точки Dy определяются путем проведения прямой из точки |
Dx |
через точку О1 до пересечения с окружностью. После измерения координат то-
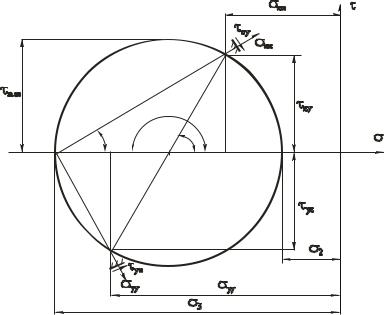
чек, видим, что значения напряжений на наклонных площадках, полученных графически и аналитическим путем, полностью совпадают. Результаты графического анализа представлены на рис. 5.27.
Рис. 5.27. Расчетная схема к определению напряженного состояния
вточке графическим методом (к примеру 5.8)
5.4.Теория деформаций
5.4.1. Тензор деформаций. Главные деформации. Относительное изменение объема
Совокупность деформаций, возникающих по разным осям и в различных плоскостях, проходящих через данную точку, определяет деформированное состояние в рассматриваемой точке.
Для исследования деформированного состояния упругого тела выделим в окрестности точки М (рис. 5.1) плоскостями параллельными координатным плоскостям элементарный параллелепипед (рис. 5.2).
Будем считать деформации очень малыми величинами. При этом условии, действие каждого из шести компонентов тензора напряженийxx ; yy ; zz ; xy ; yz ; zx вызывает возникновение деформаций по своему направ-
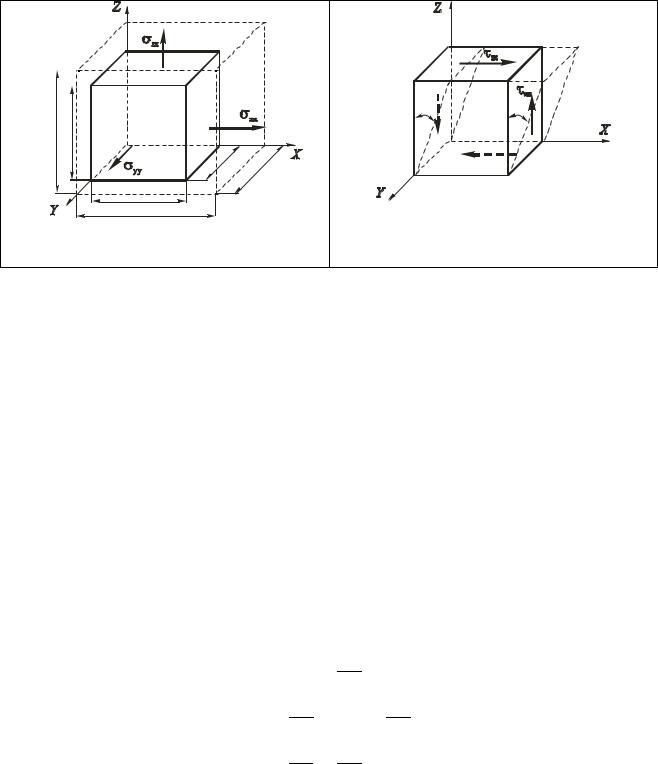
лению. Так, например, если на гранях параллелепипеда будут действовать только нормальные напряжения xx ; yy ; zz , это приведет к изменению его раз-
меров, то |
есть, развитию только линейных относительных деформаций |
xx , yy , zz |
(рис. 5.28). Если на гранях элемента действуют только касательные |
напряжения, это приводит к изменению его формы (изменению прямых углов между ребрами), то есть, возникновению угловых деформаций xy , xz , yz (рис.
5.29).
150
|
xz |
xz |
b+ b b |
|
|
с |
|
|
c+ c |
|
|
a |
|
|
a+ а |
|
|
Рис. 5.28. Расчетная схема к определе- |
Рис. 5.29. Расчетная схема к определе- |
нию линейных деформаций |
нию угловых деформаций |
Таким образом, при объемном напряженном состоянии имеют место три линейные и три угловые деформации. Относительное удлинение ребра будем обозначать с индексом, указывающим направление деформации xx , yy , zz .
Положительной величиной принимается удлинение, отрицательной – укорочение. Углы сдвига, проектируемые на плоскости:
XOY xy |
или yx ; |
XOZ xz или zx ; |
YOZ yz |
или zy . |
Изменение объема связано с линейными деформациями xx , yy , zz а изменение формы – с угловой xy , xz , yz .
Компоненты деформации xx , yy , zz ; xy , xz , yz вполне определяют деформации элементарного параллелепипеда, так как зная все составляющие можно построить модель деформированного элемента и вычислить удлинения внутри параллелепипеда по любому направлению.
Расположив все шесть компонентов деформации в определенном порядке, и поделив углы сдвига пополам, получим тензор деформации аналогично тензору напряжений.
|
|
xx , |
|
xy , |
|
|
|
|
|
|
|
xz |
|
|
|
|
|
2 |
|
2 |
|
|
TД |
yx |
, |
yy , |
yz |
(5.43) |
|
2 |
|
2 |
|
|
|
|
yz , |
|
|
|
|
|
xz , |
|
|
, |
|
|
|
2 |
|
2 |
|
zz |
|
|
|
|
|
|
|
|
|
Существуют три взаимно – перпендикулярные направления, по которым волокна или удлиняются, или укорачиваются. Они называются главными осями деформаций. Деформации в направлении главных осей называются главными деформациями. Алгоритм отыскания направляющих косинусов главных направлений деформаций ничем не отличается от алгоритма определения направляющих косинусов нормалей к главным площадкам.
Величины главных деформаций определяются уравнением
Коэффициенты уравнения (5.44) являются инвариантами деформированного состояния.
|
|
J1 |
xx |
yy |
zz |
1 |
2 |
3 |
|
|
|
|
|
|
(5.45) |
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
2 |
zy |
2 |
|
xz |
2 |
2 |
xx |
yy |
yy |
zz |
zz |
xx |
|
|
|
|
|
|
|
|
|
|
|
(5.46) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx , |
|
|
|
|
xy , |
xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J3 |
yx |
, |
|
yy , |
|
yz |
|
|
|
|
|
|
|
(5.47) |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xz |
, |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
zz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поясним физический смысл первого инварианта тензора деформаций. Выделим в окрестности рассматриваемой точки элементарный куб таким образом, что его грани будут главными площадками, а длина ребер равна единице. Объем такого куба до деформации, равный единице, обозначим V . Примем, что направление главных осей совпадает с направлением главных напряжений
(рис. 5.30).
После деформации углы параллелепипеда останутся прямыми, изменится лишь длина ребер: 1 1 ; 1 2 ; 1 3
Тогда объем после деформации:
V 1 1 1 2 1 3 .
Пренебрегая величинами второго и более порядка малости, получим:
V 1 1 2 3 .
Относительное изменение объема:
|
V |
V V |
1 |
|
2 |
|
3 |
|
xx |
|
yy |
|
zz |
J |
1 |
. |
(5.48) |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рис. 5.30. Расчетная схема к определению относительного изменения объема

Таким образом, первый инвариант тензора деформаций представляет собой относительное изменение объема. Это говорит о том, что при любой ориентации параллелепипеда в окрестности исследуемой точки, получаем одинаковое относительное изменение объема.
Относительная объемная деформация в точке равна сумме относительных линейных деформаций по трем ортогональным направлениям, проведенных через заданную точку.
5.4.2. Обобщенный закон Гука
Выделим в окрестности элементарный параллелепипед. Примем, что материал - изотропный. Возникающие деформации малы по сравнению с размерами деформируемого параллелепипеда. Деформации упругие. Все это дает возможность применить принцип независимости действия сил к вычислению деформаций.
Положим, что на элементарный параллелепипед действуют только нормальные напряжения xx 0. Тогда согласно закону Гука при одноосном рас-
тяжении, удлинение в направлении оси X равно:
xx Exx .
Укорочение в направлении осей Y и Z :
yy zz Exx .
Полагая, что действуют только нормальные напряжения yy 0 , найдем
|
yy |
|
|
|
yy . |
yy |
E |
xx |
zz |
E |
|
|
|
|
Деформации от действия напряжения zz 0 |
|
zz |
|
|
zz . |
zz |
E |
yy |
|
xx |
E |
|
|
|
|
Нормальные напряжения вызывают изменения длин ребер. Предположим, что на выделенный элемент действуют только касатель-
ные напряжения. Их действие сопровождается искажением формы элемента. Касательные напряжения yx будут вызывать изменение прямого угла в
плоскости XY на угол сдвига.
yx Gyx ; yz xz 0.
Аналогично, от действия касательных напряжений zy имеем:
zy Gzy ; xz yx 0
от касательных напряжений xz
При наличии всех компонент напряжений деформации:
xx |
1 |
xx yy zz |
|
E |
|
yy |
1 |
yy zz xx |
|
E |
|
zz |
1 |
zz xx yy |
|
E |
|
|
yx |
yx |
|
|
|
|
|
|
G |
|
|
|
|
|
zy |
zy |
G |
|
E |
(5.49) |
|
G |
2 1 |
|
|
|
|
|
|
xz |
xz |
|
|
|
|
|
|
G |
|
|
|
|
Полученные уравнения называются обобщенным законом Гука.
Если на гранях параллелепипеда действуют главные напряжения обобщенный закон Гука запишется в следующем виде
1 |
1 |
1 2 3 |
|
|
|
E |
|
|
|
2 |
|
1 |
2 |
3 1 |
(5.50) |
|
|
E |
|
|
|
3 |
|
1 |
3 |
1 2 |
|
|
|
E |
|
|
|
Для плоского деформированного состояния уравнения 5.49, 5.50 примут
вид
xx |
1 |
xx yy |
yx yx |
|
E |
|
|
E |
|
G |
(5.51) |
yy |
1 |
yy xx |
|
|
G |
|
2 1 |
|
|
E |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 2 |
|
|
|
|
|
|
E |
|
|
|
(5.52) |
|
|
|
|
1 |
2 1 |
|
|
|
2 |
|
|
|
|
|
|
|
E |
|
|
|
|
5.4.3. Потенциальная энергия деформации
Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругой деформации. Когда под действием внешней статической нагрузки тело деформируется, энергия положения груза убывает на величину, которая численно равна работе, совершаемой внешними силами. Энергия, потерянная внешними силами, не исчезает, а превращается, в основном, в потенциальную энергию деформации тела. Остальная, незначительная часть рассеивается, главным образом, в виде тепла. Потенциальная энергия де-
формации накапливается в обратимой форме – в процессе разгрузки она снова превращается в энергию внешних сил или в кинетическую энергию. Величина потенциальной энергии деформации, приходящаяся на единицу объема тела, называется удельной потенциальной энергией деформации.
Согласно закона, сохранения энергии, приращение потенциальной энергии деформации U равно уменьшению потенциальной энергии положения внешних Uп
U Uп .
Уменьшение потенциальной энергии положения внешних Uп численно
равна работе А, совершаемой ими при деформации
Uп А.
Таким образом, потенциальной энергии деформации U численно равна работе внешних сил А, совершаемой ими при упругой деформации
U А.
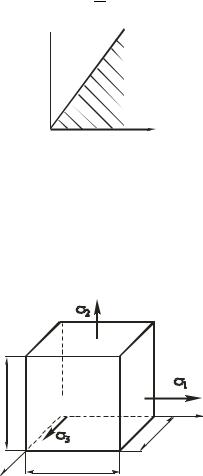
Известно, что при линейном напряженном состоянии зависимость между напряжениями и деформациями линейна (рис. 5.31), поэтому удельную потенциальную энергию деформаций можно определить:
U 21 .

Рис. 5.31. Расчетная схема к определению потенциальной энергии деформации при одноосном растяжении
Для определения удельной потенциальной энергии деформации при объемном напряженном состоянии, выделим главными плоскостями элементарный куб с размерами ребер равными 1 (рис. 5.31). Действие отброшенных частей заменим силовыми факторами.
I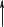

Рис. 5.32. Расчетная схема первого напряженного состояния
Так как, площадки главные, то по граням куба будут действовать только нормальные напряжения. Поскольку площади граней равны единице, то действующие в них усилия численно равны главным напряжениям.
Так как силовые факторы, действующие по главным площадкам, совершают работу только по своему перемещению, то к определению величины удельной потенциальной энергии деформации можно применить закон независимости действия сил.
При объемном напряженном состоянии удельная потенциальная энергия определится:
U 21 1 1 2 2 3 3 ,
или с учетом формул 5.50
U |
1 |
1 |
2 2 |
2 3 |
2 2 1 2 2 3 3 1 . |
(5.53) |
|
2E |
|
|
|
|
|
При деформации элемента изменяются его объем (рис. 5.28) и форма
(рис. 5.29).
Поэтому, удельную потенциальную энергию деформации можно запи-
сать:
UV - удельная потенциальная энергия изменения объема, то есть энер-
гия, накапливаемая за счет изменения объема;
Uф - удельная потенциальная энергия изменения формы, то есть энергия,
накапливаемая вследствие изменения формы.
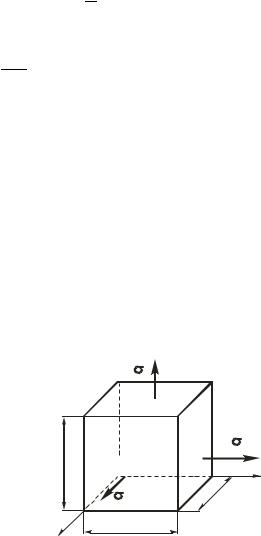
Для определения потенциальной энергии изменения объема, заменим данное напряженное состояние на другое: 1 2 3 (рис. 5.33).
II

Рис. 5.33. Расчетная схема второго напряженного состояния
В этом случае будет меняться объем без изменения формы элемента. Удельные потенциальные энергии изменения объема будут равны для двух рассматриваемых напряженных состояний, если равны их объемные деформации.
Относительная объемная деформация элементарного куба в первом случае нагружения равна:
V 1 2 3
Выражая относительные линейные деформации по формулам обобщенного закона Гука, получим:
VI |
|
1 1 2 3 2 1 2 3 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
VI |
|
1 2 1 2 3 |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
VII |
|
1 2 3 |
|
|
|
|
|
|
|
|
откуда |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
VII ; 1 2 3 . |
|
|
|
|
|
VI |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
Удельная потенциальная энергия изменения объема: |
|
UV 1 2 3 2 или UV |
|
1 2 |
1 2 |
3 2 |
(5.55) |
2E |
|
|
|
|
|
|
6 E |
|
|
|
|
|
|
|
|
Uф U UV |
|
|
|
|
Uф |
1 1 2 2 |
2 3 2 |
3 |
|
1 2 . |
(5.56) |
|
6E |
|
|
|
|
|
|
|
|
|
|
Для плоского напряженного состояния формулы 5.53, 5.55, 5.56 запи- |
шутся в следующем виде |
|
|
|
1 1 |
|
|
|
2 2 1 2 , |
|
|
|
|
|
U |
2 |
2 |
|
|
(5.57) |
|
|
|
2E |
|
|
|
|
|
|
|
|
|
UV |
|
1 2 |
|
1 2 2 , |
|
|
|
(5.58) |
|
|
|
|
6 E |
|
|
|
|
|
|
|
|
|
Uф |
|
1 1 |
2 2 2 |
2 1 |
2 . |
(5.59) |
|
|
|
|
6E |
|
|
|
|
|
|
|
|
Пример 5.9. Определить наибольшую по абсолютной величине относительную деформацию, относительное изменение объема и потенциальные энергии изменения объема и формы для стального элемента, находящегося в объемном напряженном состоянии, на гранях которого действуют главные напряжения: 1 30МПа; 2 10МПа; 3 50МПа. Расчеты произвести при сле-
дующих исходных данных: E 2 105 МПа, 0,3 .
Решение
1. Определяем величину относительных деформаций по главным направлениям ( i ,i 1,2,3 )

1 |
1 |
1 2 3 |
1 |
30 0,3 10 50 2,4 10 7 |
|
|
E |
|
2 108 |
|
2 |
|
1 |
2 3 1 |
1 |
10 0,3 50 30 2,0 10 8 |
|
|
E |
|
2 108 |
|
3 |
|
1 |
3 1 2 |
1 |
50 0,3 30 10 2,8 10 7 |
|
|
E |
|
2 108 |
|
Максимальным па абсолютной величине является относительная деформация 3 .
2. Определяем величину относительного изменения объема
V 1 2 3 2,4 10 7 0,2 10 7 2,8 10 7 0,6 10 7 .
3. Определяем потенциальные энергии изменения объема и формы
U |
V |
|
1 2 |
1 |
2 3 2 1 2 0,3 30 10 50 2 |
3 10 4 Дж |
|
|
6 E |
|
|
|
6 2 108 |
|
Uф |
1 |
1 |
2 2 |
2 3 2 3 1 2 |
|
|
|
|
|
6E |
8 30 10 2 |
10 50 2 50 30 2 104 10 4 Дж |
|
6 |
1 0,3 |
|
|
|
2 10 |
|
|
|
|
|
2.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Какие напряжения возникают на гранях элементарного параллелепипеда при объемном напряженном состоянии?
2.Какие индексы используются при обозначении нормальных напря-
жений?
3.Какие индексы используются при обозначении касательных напря-
жений?
4.Какое правило знаков используется для нормальных напряжений при объемном напряженном состоянии?
5.Какое правило знаков используется для касательных напряжений при объемном напряженном состоянии?
6.Какое количество компонент напряжений образует тензор напряже-
ний?
7.Какое количество компонент напряжений необходимо знать для определения напряженного состояния в точке?
8.Сформулируйте закон парности касательных напряжений.
9.Какими параметрами задается положение наклонной площадки в
тетраэдре?










 3
3