
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра
.pdf
5.2. Объемное напряженное состояние
5.2.1. Определение напряжений на наклонных площадках. Главные площадки. Главные напряжения.
Покажем, что задание шести компонентов тензора напряжений определяет полностью напряжённое состояние в точке, т.е. величину вектора напряжений на любой площадке.
|
Z |
|
|
|
|
d Ax |
|
dAy |
yy |
|
|
|
|
|
|
P |
|
|
|
yx |
|
|
|
|
xy |
|
|
|
|
|
yz |
|
|
|
|
xx |
|
zy |
|
|
|
xz |
|
|
|
Х |
|
|
zx |
dA |
|
||
|
|
|
|
||
|
zz |
|
|
|
|
Y dAz |
|
|
|
||
|
|
|
|
|
|
.
Рис. 5.4. Расчетная схема к определению напряжений на наклонной площадке
Для решения поставленной задачи вырежем в окрестности точки M элементарный тетраэдр (рис. 5.4). Три его грани совпадают с координатными плоскостями системы XOZ , XOY , ZOY . Четвертая грань является наклонной. Направление нормали к наклонной плоскости характеризуется направляющими косинусами:
cos x, l |
|
|
cos y, m |
(5.3) |
|
cos z, n |
|
|
|
|
|
l2 m2 n2 |
1 |
|
Действие отброшенных частей заменим силовыми факторами. Полное напряжение, действующее на наклонной грани обозначим через Р , а его проекции на
координатные оси Px ; Py ; Pz .
Площади элементарных граней обозначим: dAx ;dAy ;dAz ;dA .
Проекции полного напряжения, действующего на наклонной грани с внешней нормалью и направляющими косинусами l, m, n определяются соотношениями
Px |
xxl yx m zx n |
|
Py xyl yy m zy n |
(5.4) |
|
Px |
xzl yz m zx n |
|
Полное напряжение можно определить:
P2 |
P2 |
P2 |
P2 . |
(5.5) |
|
x |
y |
z |
|
Проецируя вектор полного напряжения на нормаль и ось t , лежащую в плоскости площадки получаем формулы для нормальных и касательных
напряжений, действующих на этой площадке
xxl2 yy m2 zz n2 2 yxlm 2 zy mn 2 zx nl |
(5.6) |
129
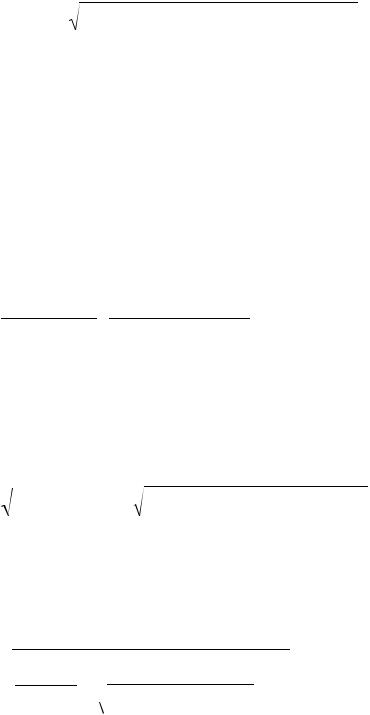
|
|
|
(P2 |
P2 |
P2 ) (P |
l P |
m P |
n)2 . |
(5.7) |
|
|
|
x |
y |
z |
x |
y |
z |
|
|
|
При изменении ориентации площадки напряжения на ней будут изменяться.
Пример 5.2. На наклонной площадке элемента, рассмотренного в примере 5.1, нормаль к которой составляет с осями X и Y соответственно углы
1 60 , и 2 40 , определить величины полного напряжения P и его проекций на координатные оси Px , Py , Pz , а также величины нормального и касательного напряжений.
Решение
1. Определяем величины направляющих косинусов
l cos x, cos60 0,5; m cos y, cos 40 0,766; n 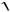
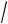 1 l2 m2
1 l2 m2 
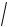 1 0,52 0,7662 0,404
1 0,52 0,7662 0,404
2. Определяем величины полного напряжения P и его проекций на координатные оси Px , Py , Pz
|
Px |
xxl yxm zx n 60 0,5 9 0,404 26,364 МПа; |
|||
|
Py |
xyl yy m zy n 12 0,766 9 0,404 5,556 МПа; |
|||
|
Px |
xzl yz m zx n 9,0 0,5 |
9 0,766 10 0,404 1,646 МПа; |
||
P |
|
P2 |
P2 |
P2 26,364 |
2 5,5562 1,6462 26,99 МПа. |
|
|
x |
y |
z |
|
3. |
Определяем величины нормального и касательного напряже- |
||||
ний.
xxl2 yy m2 zz n2 2 yxlm 2 zy mn 2 zx nl
60,0 0,52 12,0 0,7662 10,0 0,4042 2 9,0 0,766 0,404 2 9 0,5 0,404
8,261
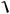
 (P2x P2y P2z ) (Pxl Py m Pz n)2
(P2x P2y P2z ) (Pxl Py m Pz n)2
 P2 2
P2 2 
 26,992 8,261 2 25,69 МПа.
26,992 8,261 2 25,69 МПа.
Каково бы ни было напряженное состояние в рассматриваемой точке, всегда существуют три взаимно перпендикулярных площадки, на которых касательные напряжения равны нулю, а нормальные напряжения имеют стационарные значения (максимум, минимум, минимакс).
Эти площадки называются главными. Нормальные напряжения, действующие на главных площадках, называются главными напряжениями.
Исходя из определения, найдем главные напряжения и положения главных площадок.
Главные напряжения являются корнями кубического уравнения
130

|
|
|
|
|
xx , |
yx , |
|
|
|
zx , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xy , |
yy , |
|
|
zy , |
|
0, |
|
|
|
|
|||||||
|
|
|
|
|
|
xz , |
yz , |
|
zz , |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 ( |
xx |
|
yy |
|
zz |
) ( |
|
yy |
|
zz |
|
zz |
|
xx |
2 |
2 |
2 |
) |
|||||
|
|
|
|
|
|
xx yy |
|
|
|
|
|
|
xy |
yz |
zx |
(5.8) |
|||||||
( |
|
|
2 |
2 |
|
2 |
2 |
|
) 0. |
|
|
||||||||||||
zz |
zx |
|
|
|
|||||||||||||||||||
xx yy |
|
|
xx |
yz |
|
|
yy xz |
zz |
yx |
|
|
xy |
yx |
|
|
|
|
|
|
|
|||
В силу симметрии элементов определителя относительно его главной диагонали решение этого уравнения дает три действительных корня, представляющих собой три главных напряжения.
Главные напряжения впредь будем обозначать: 1; 2 ; 3 ; при этом по-
лагают, что между указанными напряжениями существует следующее соотношение (в алгебраическом смысле) 1 2 3 .
Вокруг рассматриваемой точки M (рис. 5.1), можно вырезать бесчисленное множество бесконечно малых элементов (параллелепипед), грани которых будут различно ориентированы по отношению к осям координат. При изменении ориентации граней параллелепипеда компоненты тензора напряжений будут меняться. Но независимо от способа вырезания элемента вокруг данной точки подстановка значений компонент напряжения в уравнение (5.8) должна дать одни и те же значения главных напряжений, т. к. последние определяются характером напряженного состояния. Коэффициенты уравнения (5.8) называются инвариантами напряженного состояния.
Перепишем уравнения (5.8) в виде
3 J 2 |
J |
2 |
J |
3 |
0 , |
(5.9) |
1 |
|
|
|
|
где J1, J2 , J3 - первый, второй, третий инварианты напряженного состояния или инварианты тензора напряжений.
|
|
|
|
J |
1 xx yy zz |
|
|
|
|
|
|
(5.10) |
|||||
J |
2 |
|
|
yy |
|
|
zz |
|
|
|
2 |
|
2 |
|
2 |
(5.11) |
|
|
|
xx |
|
|
yy |
|
zz xx |
|
xy |
|
yz |
|
zx |
|
|||
|
|
|
|
|
xx ; yx ; zx |
|
|
|
|
|
|
|
|
||||
|
|
J3 |
xy ; yy ; zy |
|
|
|
|
|
|
|
(5.12) |
||||||
xz ; yz ; zz
Втеории напряжений, а так же в теории деформации инварианты являются основными характеристиками напряженного и деформированного состояния в точке. Компоненты тензора напряжений как величины, связанные с осями координат, считаются вспомогательными.
Внекоторых случаях инварианты тензора напряжений могут принимать нулевые значения.
131
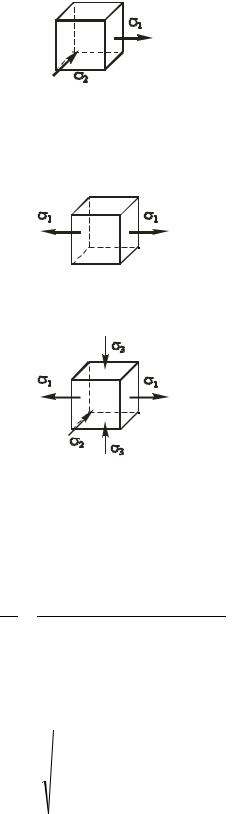
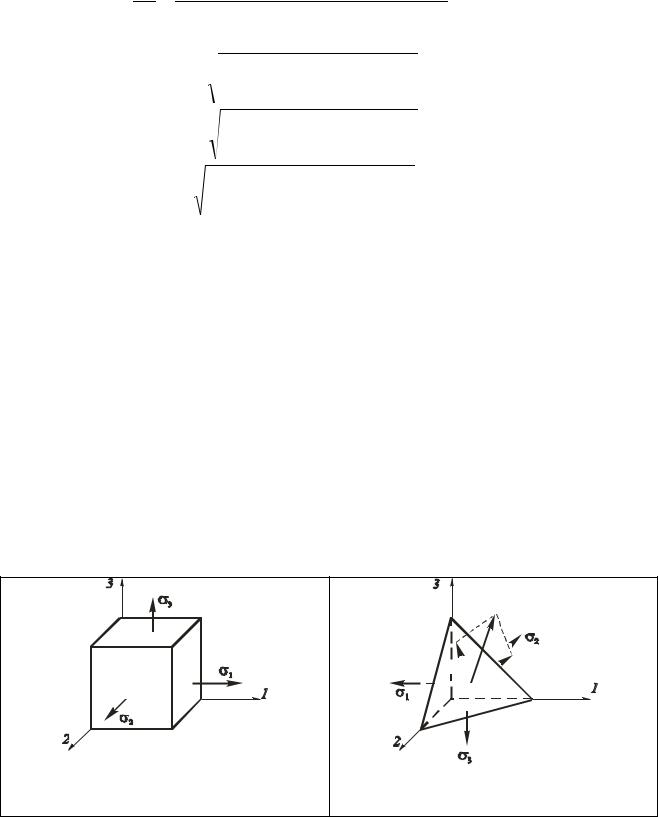
1. J3 0 . Один из корней уравнения (5.9) так же равен нулю. Имеет место плоское напряженное состояние (рис. 5.5).
Рис. 5.5. Расчетная схема плоского напряженного состояния
2. J2 J3 0 два корня уравнения (5.9) равны 0. В этом случае имеет место линейное напряженное состояние (рис. 5.6).
Рис. 5.6. Расчетная схема одноосного напряженного состояния
3. J 1 0, J 2 0, J 3 0.Объемное напряженное состояние (рис. 5.7).
Рис. 5.7. Расчетная схема объемного напряженного состояния
Положение главных площадок определяется направляющими косинусами li , mi , ni i 1,2,3 , которые ориентируют главные направления напряже-
ний:
li |
|
yy i zx zy yx |
, |
|
||||||
ni |
xy2 xx i yy i |
|
||||||||
m |
|
|
xx i zy zx yx |
|
||||||
i |
xy2 |
xx i yy i , |
(5.12) |
|||||||
ni |
|
|||||||||
ni |
|
|
|
1 |
|
|
, |
|
|
|
|
2 |
m |
2 |
|
|
|||||
|
|
|
l |
1 |
|
|
||||
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
Здесь i - номер главной площадки.
132

Пример 5.3. Определить величину и направление главных напряжений в точке М в окрестности которой действуют следующие координатные напряже-
ния: xx |
60МПа; |
yy 12МПа; |
zz |
10МПа; |
xy 0; |
yz 9МПа; |
|||||||||||
zx 9МПа.. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
||
1. |
Определяем инварианты напряженного состояния |
|
|||||||||||||||
J1 |
xx yy |
zz |
60 12 10 38 МПа; |
|
|
||||||||||||
J |
2 |
|
yy |
|
|
zz |
|
xx |
|
2 |
2 |
|
2 |
|
|
||
|
xx |
|
yy |
zz |
|
|
|
xy |
yz |
|
zx |
|
|
||||
60,0 12,0 12,0 10,0 10,0 60,0 9,0 2 9,0 2 |
1362 МПа; |
||||||||||||||||
J |
3 |
|
2 2 2 |
2 |
|
|
|||||||||||
|
xx |
yy zz |
|
xx |
yz |
|
yy |
xz |
zz yx |
|
xy yz zx |
|
|
||||
60,0 12,0 10,0 60,0 9,0 2 12,0 9,02 3312 МПа.
2.Решая кубическое уравнение (5.9) относительно главных напря-
жений i |
i 1,2,3 , получаем |
1 20,517МПа; |
3 2,64МПа; |
3 61,156МПа.
Производим проверку правильности, полученного решения уравнения, инвариантному по отношению к преобразованию координат.
J1 xx yy zz 1 2 3 20,517 2,64 61,156 38,0 МПа;
J2 xx yy yy zz zz xx xy 2 yz 2 zx 2 1 2 2 3 3 1
20,517 2,64 2,64 61,156 61,156 20,517 1362,0 МПа;
J3 xx yy zz xx yz2 yy xz2 zz yx2 2 xy yz zx
20,517 2,64 61,156 3312,0 МПа.
3. Определяем по формулам 5.12 величину направляющих косинусов
l1 |
|
|
12,0 20,517 9,0 9,0 0 |
|
|
n |
|
02 |
60,0 20,517 12,0 20,517 0,11178 |
; |
|
1 |
|
|
12,0 2,64 9,0 9,0 0 |
|
|
|
l2 |
|
|
|
|
|
n2 |
|
02 60,0 2,64 12,0 2,64 0,14368 |
; |
|
l2 |
|
|
12,0 61,156 9,0 9,0 0 |
|
|
n2 |
|
02 60,0 61,156 12,0 61,156 7,7832 |
; |
||
m |
|
|
60,0 20,517 9,0 9,0 0 |
|
|
n1 |
|
02 60,0 20,517 12,0 20,517 1,0567 ; |
|||
1 |
|
|
60,0 2,64 9,0 9,0 0 |
|
|
|
m |
|
|
|
|
|
n |
2 02 60,0 2,64 12,0 2,64 0,9615 |
; |
|
|
|
2 |
|
|
|
|
133
m |
|
|
60,0 61,156 9,0 9,0 0 |
|
|||||||
n3 |
|
02 60,0 61,156 12,0 61,156 0,1230 |
; |
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
1 |
|
|
0,685 ; |
|
|
|
0,111782 1,0567 2 |
1 |
|
|||||||
|
|
n2 |
|
|
|
|
1 |
|
|
0,717 ; |
|
|
|
0,14368 2 |
0,9615 2 |
1 |
|
||||||
|
n3 |
|
|
|
|
|
1 |
|
|
0,12742. |
|
|
7,78324 2 |
0,1230 2 |
1 |
|
|||||||
Тогда направляющие косинусы li и mi |
определяются по формулам |
||||||||||
|
|
l |
n |
li |
и |
m |
n |
mi , где i 1,2,3; |
|
||
|
|
i |
i |
n |
|
i |
i |
n |
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
l1=0,0766; |
|
|
m1 0,724 ; |
|
|||||
|
|
|
l2 =-0,103; |
|
|
m2 0,689 ; |
|
||||
|
|
|
l3 =-0,992; |
|
|
m3 |
0,017 . |
|
|||
Формулы для напряжений на произвольной площадке существенно упрощаются, если в качестве исходного выбрать элементарный параллелепипед, на гранях которого действуют только главные напряжения. Совместим координатные оси X ,Y, Z с главными направлениями 1,2,3 (рис. 5.8) и определим напряжения на наклонной площадке, нормаль к которой составляет с координатными осями углы 1 , 2 , 3 (рис. 5.9). Тогда направляющие косинусы будут
равны: l cos 1; m cos 2 ; n cos 2 .


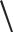


Рис. 5.8. Расчетная схема объемного |
Рис. 5.9. Схема к определению напря- |
напряженного состояния |
жений на наклонной площадке |
|
Проекции полного напряжения на наклонной площадке получим из формулы 5.4.
P 1 1l; |
P 2 2m; |
P 3 3n |
(5.13) |
Тогда полное напряжение будет равно
134
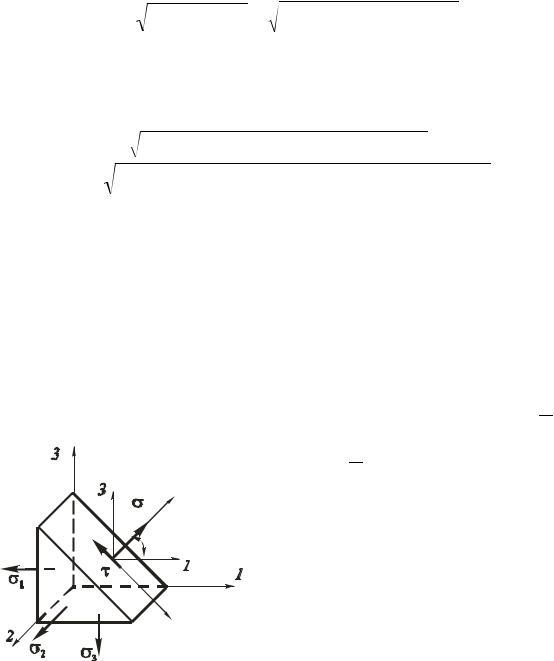
P |
P2 |
P2 |
P2 |
|
l 2 |
|
2 |
m 2 |
3 |
n 2 |
(5.14) |
|
x |
y |
z |
|
1 |
|
|
|
|
Нормальные и касательные напряжения определяем соответственно из формул 5.6, 5.7
|
|
|
|
|
|
l2 |
|
2 |
m2 |
|
3 |
n2 |
|
|
|
|
|
|
(5.15) |
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(P2 |
P2 |
|
P2 |
) (P l P |
m P |
|
n)2 |
|
|
|
|
|||||||||||
|
1 |
2 |
|
|
3 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|||||
|
|
( l 2 |
|
2 |
m 2 |
3 |
n 2 ) ( l2 |
|
2 |
m2 |
3 |
n2 )2 |
(5.16) |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
5.2.2. Графический анализ напряженного состояния в точке. Круги Мора. Максимальные касательные напряжения.
Напряжения на наклонных площадках можно определить графически (с помощью кругов Мора). Пусть известны главные напряжения на гранях параллелепипеда и положение наклонных площадок. Рассмотрим поочередно наклонные площадки параллельные одному из главных напряжений. Так, пло-
щадка, показанная на рис. 5.10, параллельна |
2 . Здесь при 1 ; 3 |
|
; |
||||
|
|
|
|
|
2 |
|
|
|
2 |
, из формулы 5.13 получим: |
|||||
|
|
2 |
1 cos ; |
P 3 3 sin ; |
|||
|
P 1 |
||||||
|
|
P 2 |
0 . |
|
|
||
|
|
|
|
|
|||
|
|
Нормальные и касательные |
|||||
|
|
|
|||||
|
напряжения из формул 5.15, 5.16 |
||||||
будут равны: |
|
|
|
||||
|
|
|
|
||||
|
|
1 cos2 3 sin2 |
(5.17) |
||||
|
|
|
1 3 sin 2 |
(5.18) |
|||
Рис. 5.5. Расчетная схема к определению |
|
|
|
2 |
|
|
|
|
|
Из этих |
формул следует, |
||||
напряженного состояния на наклонной |
|
|
|||||
что |
главное напряжение |
2 |
не |
||||
площадке, параллельной главному на- |
|||||||
влияет на напряженное состояние |
|||||||
пряжению |
на этой площадке. Далее рассмот- |
||||||
|
|||||||
|
рим |
некоторую |
геометрическую |
||||
плоскость и отнесем ее к прямоугольным координатным осям и . Отклады-
ваем в некотором масштабе значения главных напряжений OA 1 |
и OB 3 |
||
(рис. 5.11). На AB как на диаметре строим окружность с центром в точке O2 на |
|||
расстоянии OO 1 3 |
от начала координат радиусом равным R 1 3 . |
||
2 |
2 |
2 |
2 |
|
|
||
Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках параллельных напряжению 2 . Аналогичным
135
образом рассматриваем два других семейства площадок параллельных соответ-
ственно |
главным напряжениям 1 |
и 3 , и строим круги радиусами |
|||
R 2 |
3 |
и R 1 2 |
. Совокупность точек этих окружностей описывает |
||
1 |
2 |
3 |
2 |
|
|
|
|
|
|
||
напряженное состояние всех сечений, проведенных в элементе параллельно соответственно напряжениям 1 , 2 и 3 .
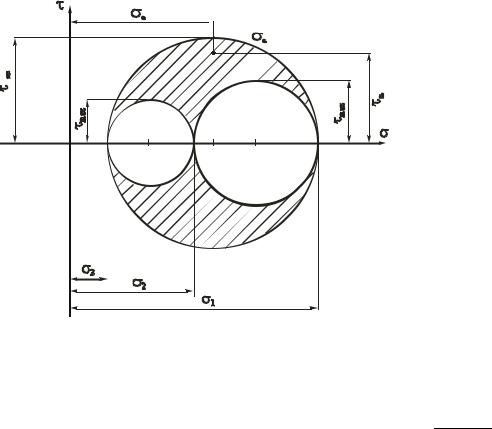
Напряженное состояние на площадках, пересекающих все три главные напряжения, изображаются точками D , попадающими в заштрихованную об-
ласть рис. 5.11.
II
 D
D
D 
|
|
III |
I |
|
|
O B |
O1 С O2 O3 |
А |
Рис. 5.11. Графическое изображение напряженного состояния в точке
Точкой, |
в которой действуют максимальные касательные напряжения |
||
является точка |
D . Эта точка лежит на окружности радиусом R 1 3 |
, а |
|
|
2 |
2 |
|
|
|
|
|
максимальное касательное напряжение max действует на площадке параллель-
ной главному напряжению 2 |
и наклоненной под углом 45 к главным на- |
|||
пряжениям 1 |
и 3 , что следует из формулы 5.18 (рис. 5.12) и определяется по |
|||
формуле |
|
|
1 3 |
|
|
|
maxII |
(5.19). |
|
|
|
|
2 |
|
136

450 |
II |
Рис. 5.12. Схема к определению максимального касательного напряжения
На двух других семействах площадок параллельных соответственно главным напряжениям 1 и 3 будут определяться по формулам
maxI |
|
2 3 |
, |
maxIII |
|
1 2 |
(5.20). |
|
|
2 |
|
|
|
2 |
|
Если площадка проходит через две главные оси, то она совпадает с третьей главной площадкой, таким образом, на этой площадке касательное напряжение отсутствуют, а нормальное напряжение является главным. Точками, соответствующими главным площадкам на рис. 5.11 являются А, В, С.
Используя круги Мора, и зная ориентацию площадки по отношению к главным осям, можно найти составляющие и полного напряжения, дейст-
вующего на этой площадке. Для этого вычисляются радиусы окружностей r1 , r2 , r3 с центрами соответственно в точках O1 , O2 , O3
r |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
l2 |
, |
|
|||||
|
|
2 |
|
|
3 |
|
|
1 |
2 |
1 |
3 |
|
||||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
r |
|
3 1 |
2 |
|
2 |
|
3 |
|
2 |
|
m2 |
, |
(5.21). |
|||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r3 |
|
|
|
|
|
2 |
|
3 |
1 3 2 n2 . |
|
||||||||||||||
|
|
1 |
2 |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Координаты точек этих окружностей равны значениям |
и , дейст- |
|||||||||||||||||||||||
вующих на площадках, проходящих через рассматриваемую точку напряженно-
го |
тела, нормали к которым составляют одинаковые углы с осью X - |
1 |
ar cosl (окружность радиусом r1 ), с осью Y - 2 ar cosm (окружность ра- |
диусом r2 ), с осью Z - 3 ar cosn (окружность радиусом r3 ).
Для задания ориентации площадки необходимы значения двух направляющих косинусов. Значение третьего определяется из соотношения 5.3. По заданным значениям главных напряжений 1 , 2 и 3 в масштабе строятся круги
Мора и вычисляются два любых радиуса ri по формулам 5.21. Далее из центров соответствующих окружностей Oi проводятся радиусами ri дуги окружностей
(рис. 5.13).
137

Точка пересечения этих дуг характеризует напряженное состояние ( и) на площадке, нормаль к которой составляет углы 1 , 2 , 3 с координатными осями.
 D D
D D 
r2
r3
O B |
O1 |
O2 O3 |
А |
Рис. 5.13. Схема к определению напряженного состояния на наклонной площадке
Пример 5.4. Произвести графическое определение напряженного состояния в точке, если известны главные напряжения на гранях параллелепипе-
да, |
выделенного в ее окрестности равны: 1 60МПа; |
2 10МПа; |
3 |
20МПа. Определить величину составляющих и полного напряже- |
|
ния, действующего на площадке нормаль к которой составляет с координатными осями углы 1 60 , 2 70 . Определить величину максимального касательного напряжения max .
Решение
1.В масштабе по заданным значениям главных напряжений строим круги Мора (рис. 5.14).
2.По формулам 5.21 определяем величину радиусов окружностей r1 и
r2
|
|
r |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
l2 |
|
|||||
|
|
|
|
|
2 |
|
|
3 |
|
|
1 |
2 |
1 |
3 |
|||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
10 20 |
2 |
|
|
60 10 60 |
20 |
|
cos60 |
|
|
2 |
|
||||||||||||
|
2 |
|
|
|
|
35,0МПа, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
||
|
|
|
|
3 |
|
1 |
|
|
2 |
3 |
2 |
|
1 |
|
|||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
138
