Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра

3.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какой изгиб называется плоским косым?

2.Какой изгиб называется пространственным косым?

3.Сочетанием каких видов изгиба является косой изгиб?

4.Что такое силовая линия для балки при косом изгибе?

5.По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при косом изгибе, как устанавливаются знаки этих напряжений?

6.Как находиться положение нулевой линии при косом изгибе балки?

7.Какие точки в сечении балки являются опасными и как определяется их положение при косом изгибе для пластичных материалов?

8.Объясните, как подбирается круглое поперечное сечение балки при косом изгибе.

9.Объясните, как подбирается прямоугольное поперечное сечение балки при косом изгибе.

10.Какие точки в сечении балки являются опасными и как определяется их положение при косом изгибе для хрупких материалов?

11.Как строятся эпюры нормальных напряжений при косом изгибе балки?

12.Как определяются перемещения точек оси балки при косом изгибе?

13.В чём состоит проверочный расчёт на жёсткость при косом изгибе?

14.Для каких видов сечений и каких случаев нагружения невозможен косой изгиб?

89

4. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

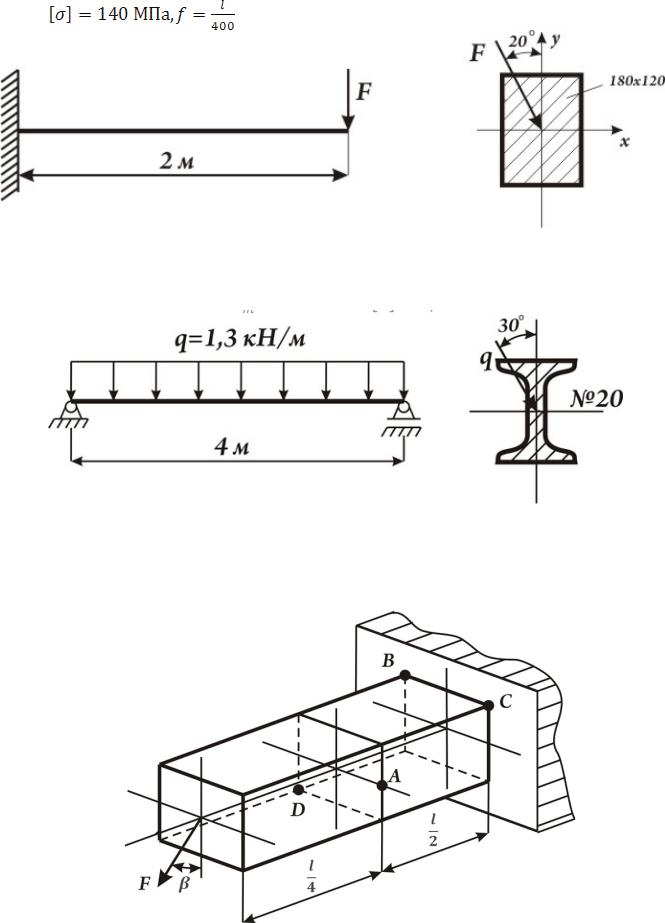
1. Проверить прочность и жёсткость стальной балки, если

.

Рис. к задаче 1

2.Проверить прочность стальной балки и вычислить максимальный прогиб, если предел текучести

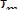
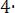
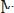
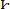
Рис. к задаче 2

3.Вычислить нормальное напряжение в точках A,B,C,D, указанных на рисунке:

Рис. к задаче 3

90

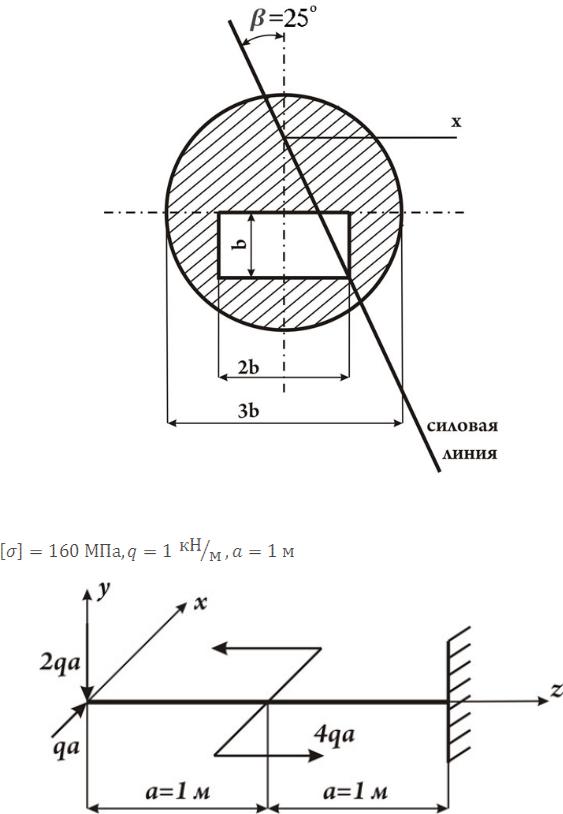
4.Определить положение нулевой (нейтральной) в опасном поперечном сечении и построить эпюру нормальных напряжений

Рис. к задаче 4

5. Вычислить диаметр балки, исходя из условия прочности, если

Рис. к задаче 5

91

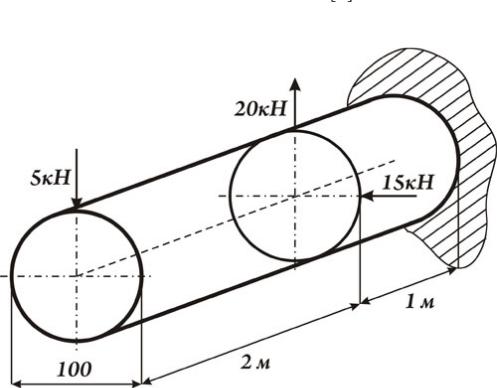
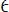
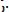
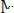
6.Проверить прочность стального бруса при . Определить полное перемещение свободного конца бруса

Рис. к задаче 6

92

5.ВЫВОДЫ

1.Плоский косой изгиб бруса возникает под действием нагрузок, плоскость действия которых (силовая плоскость) не совпадает ни с одной из его главных плоскостей. При этом виде изгиба упругая линия бруса – плоская кривая, не лежащая в силовой плоскости.

2.Пространственный косой изгиб возникает под действием нагрузок, действующих в разных плоскостях. При этом виде изгиба упругая линия бруса представляет собой пространственную кривую линию

3.Как плоский, так и пространственный случаи косого изгиба можно рассматривать как сочетание двух прямых изгибов в главных плоскостях инерции бруса. Все внешние силы и моменты, действующие на брус, следует разложить на составляющие по главным центральным осям его поперечного сечения и построить соответствующие эпюры изгибающих моментов (эпюры Мx и Мy).

4.Задача об определении напряжений и перемещений решается на основе принципа независимости действия сил: вычисленные напряжения алгебраически складываются в каждой интересующей точке; перемещения складываются векторно.

5.Силовая и нулевая линии всегда проходят через противоположные квадраты поперечного сечения и через центр тяжести сечения.

6.Наибольшие нормальные напряжения возникают в тех точках поперечного сечения, которые наиболее удалены от нулевой линии.

93

РАЗДЕЛ 4 РАСЧЕТ БРУСА БОЛЬШОЙ ЖЕСТКОСТИ НА ПРОЧНОСТЬ

ПРИ ВНЕЦЕНТРЕННОМ РАСТЯЖЕНИИ-СЖАТИИ

Основные теоретические сведения и расчетные формулы

4.1. Определение напряжений и положения нулевой линии.

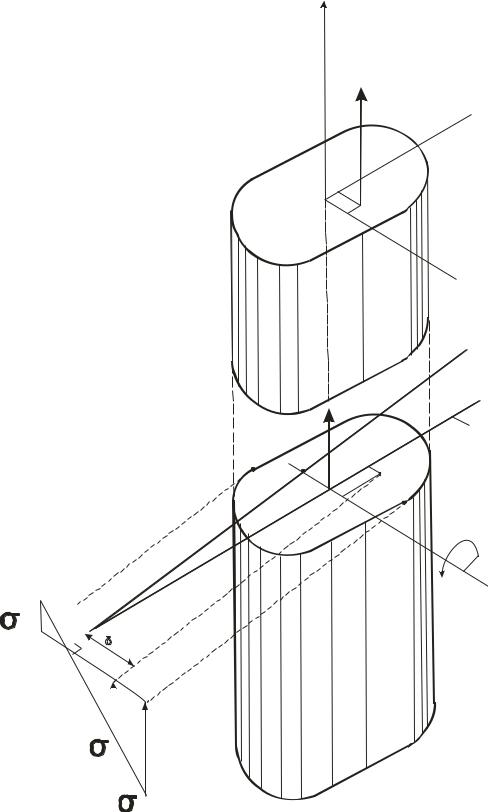
Рассмотрим массивный брус постоянного поперечного сечения, растянутый двумя силами Р, параллельными его оси и пересекающими любое поперечное сечение в точке М с положительными координатами х0 и у0 относительно главных центральных осей х, у сечения* (рис.4.1.). Очевидно, что величины внутренних сил во всех поперечных сечениях бруса одинаковы, и напряжения в этих сечениях можно определять, пользуясь принципом сложения действия сил.

В каждом поперечном сечении бруса возникают три внутренних силовых фактора:

Все три фактора вызывают в произвольной точке k с положительными координатами х и у растягивающие (положительные) напряжения (рис.4.1.). Поэтому нормальное напряжение в произвольной точке k (x, y) равно сумме напряжений от продольной силы N и изгибающих моментов Mx и Mу [2], т.е.

инерции сечения, получим следующее выражение для определения напряжений при внецентренном растяжении-сжатии:

___________________

* - Здесь учтено, что деформациями изгиба массивных брусьев большой жесткости можно пренебречь [1]

94

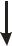Рис.4.1. Схема распределения нагрузки в сечениях бруса большой жесткости при внецентренном растяжении

95

В формулу (4.3) величина растягивающей силы Р подставляется со знаком плюс, а сжимающей – со знаком минус; координаты х0 , у0, х и у в эту формулу подставляются со своими знаками.

Если вычислить нормальные напряжения во всех точках сечения и отложить их в виде векторов, то концы векторов образуют плоскость, которая называется поверхностью напряжений [3, 4]. Поверхность напряжений пересекает плоскость поперечного сечения по прямой, точки которой свободны от напряжений. Эту прямую называют нулевой линией или нейтральной осью.

Уравнение нулевой линии получим, приняв в выражении (4.3) равным нулю:

Это уравнение прямой, не проходящей через начало координат. Записывая уравнение (4.4) как уравнение прямой в отрезках [5]:

где

- отрезки, отсекаемые нулевой линией на осях координат х и у, получаем простой способ построения нулевой линии по заданным координатам точки М (х0 , у0), которую называют полюсом. Находятся отрезки a и b и откладываются по осям координат от начала. Через концы отрезков проводят

96

например, сила Р приложена в точке М первого квадранта, то нулевая линия n-n отсечет треугольник на осях координат в третьем квадранте.

Если в равенствах (4.5) поменять местами отрезки и координаты, то справедливость равенств не нарушится:

Отсюда можно заключить, что, приложив силу в точке М с координатами a и b (рис.4.2), мы получаем новое положение нулевой линии n n , которая отсечет на осях х, у отрезки, равные координатам х0 , у0 точки М.

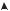у

n‘

n

х0 М

у0

а

х

в

n

Рис.4.2. Свойство взаимности отрезков a и b и координат полюса x0 и y0

Иначе говоря, отрезки a, b и координаты х0 , у0 обладают свойством взаимности. Заметим также, что положение нулевой линии в заданном сечении зависит только от координат х0 , у0 точки приложения силы Р и не зависит от величины и знака этой силы. С увеличением координат, т.е. с удалением точки приложения силы (х0 , у0) от центра тяжести сечения, отрезки a и b уменьшаются и нулевая линия приближается к центру тяжести сечения. С приближением точки (х0 , у0) к центру тяжести нулевая линия удаляется от сечения. В пределе, когда х0 = у0=0 мы будем иметь осевое растяжение –

97

сжатие. Нулевая линия при этом удаляется в бесконечность и плоскость напряжений будет параллельна плоскости сечения.

При внецентренном растяжении и сжатии нормальные напряжения в каждой точке поперечного сечения бруса, как и при изгибе, прямо пропорциональны расстоянию δ от этой точки до нейтральной оси. Наибольшие напряжения возникают в точках 1 и 2 поперечного сечения, наиболее удаленных от нейтральной оси (рис.4.1.).

При некоторых значениях координат х0 , у0 нулевая линия может касаться контура сечения, не пересекая его (рис.4.3.).

у

D

М(Х0,У0)

х n

max

С

Р/F

n

Рис.4.3. Эпюра напряжений для случая касания нулевой линии и контура сечения

При этом напряжение в точке касания С равно нулю, а в наиболее удаленной от нулевой линии точке сечения D – наибольшее. Эпюра напряжений имеет треугольный вид. На этом случае, имеющим большой практический интерес, остановимся ниже.

98