
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра
.pdf5. В силу, какого закона тензор напряжений является симметричным?
11.Какие напряжения могут возникать на наклонной площадке?
12.Какие напряжения возникают на главной площадке?
13.Какие площадки называются главными?
14.Какое соотношение должно выполняться между главными напря-
жениями?
15.Решением, какого уравнения являются корни кубического уравне-
ния?
16.Почему коэффициенты и свободный член уравнения, составленного для определения главных напряжений, являются его инвариантами?
17.Какие частные случаи решения уравнения, составленного для определения главных напряжений, могут иметь место?
18.Какие параметры определяют положение главных площадок?
19.На каких площадках возникают максимальные касательные напря-
жения?
20.По какой формуле вычисляются максимальные касательные напря-
жения?
21.Параллельно, какому напряжению будут площадки, если их напря-
женное состояние описано окружность радиусом 1 2 ?
2
22.Параллельно, какому напряжению будут площадки, на которых действуют максимальные касательные напряжения?
23.Какие площадки называются октаэдрическими?
24.На какие слагаемые раскладывается тензор напряжений?
25.Какую деформацию характеризует шаровой тензор напряжений?
26.Какую деформацию характеризует тензор девиатор напряжений?
27.С какой целью тензор напряжений разбивается на две части?
28.Какой вид напряженного состояния называется плоским?
29.Какие виды плоского напряженного состояния имеют место?
30.Какие правила знаков используются для напряжений при плоском напряженном состоянии?
31.По какой формуле определяется максимальное касательное напряжение при плоском напряженном состоянии?
32.По какой формуле определяются главные напряжения при плоском напряженном состоянии?
33.По какой формуле определяется положение главных площадок при плоском напряженном состоянии?
34.Какие компоненты деформаций полностью определяют деформированное состояние в точке?
35.Запишите тензор деформаций для объемного напряженного состоя-
ния.
36.Возникновение, каких деформаций приводит к изменению формы
элемента?
37.Какие три взаимно перпендикулярные направления называются
главными?
159
38.Каким уравнением следует пользоваться для определения главных деформаций?
39.Как определяют инварианты деформированного состояния?
40.Какой физический смысл имеет первый инвариант деформации?
41.Запишите обобщенный закон Гука для объемного напряженного состояния через главные напряжения.
42.Чему числена, равна потенциальная энергия деформации?
43.Чему равна потенциальная энергия деформации при объемном напряженном состоянии?
44.На какие составляющие делится потенциальная энергия деформа-
ции?
3.ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1.Записать тензор напряжений и изобразить элемент, на гранях кото-
рого действуют эти напряжения: xx 20МПа; |
yy 40МПа; |
zz 10МПа; |
||||
xy 20МПа; yz 15МПа; zx 9МПа. |
|
|
|
|
|
|
|
|
20 |
0 |
0 |
|
|
3.2. Тензор напряжений задан в главных осях |
|
0 |
10 |
0 |
|
|
Тн |
. |
|||||
|
|
|
0 |
0 |
|
|
|
|
|
25 |
|||
Требуется:
1.Изобразить в аксонометрии и элемент и показать на его гранях действующие напряжения
2.Разложить тензор на шаровой тензор и тензор девиатор,
3.Найти наибольшие касательные напряжения,
4.Найти октаэдрические напряжения,
5.Определить направляющий cosl .
3.3. В окрестности точки заданы напряжения xx 20МПа;
yy 10МПа; zz 0; xy 25МПа; yz 0; zx 0.
160
1.Показать на гранях элемента, действующие напряжения,
2.Определить величину и направление главных напряжений,
3.Определить величину напряжений, действующих на площадке, нор-
маль к которой составляет угол 30 с осью X.
3.4. В окрестности точки заданы напряжения xx 20МПа;
yy 30МПа; zz 0; xy 5МПа; yz 0; zx 0.
1.Показать на гранях элемента, действующие напряжения,
2.Определить величину и направление главных напряжений,
3.Определить величину напряжений, действующих на площадке, нор-
маль к которой составляет угол 60 с осью 1.
Расчеты произвести графическим методом.
3.5. Определить наибольшую по абсолютной величине относительную деформацию, относительное изменение объема и потенциальные энергии изменения объема и формы для стального элемента, находящегося в объемном напряженном состоянии, на гранях которого действуют напряжения:
xx 50МПа; |
yy 10МПа; |
zz 30МПа; |
xy 20МПа; |
yz |
15МПа; |
zx 10МПа. |
Расчеты произвести при следующих исходных |
данных: |
|||
E 2 105 МПа, |
0,3 . |
|
|
|
|
3.6. В стальном элементе, испытывающем плоское напряженное состоя- |
|||||
ние, известны |
величины |
относительных |
деформаций |
xx 6,3 10 4 , |
|
yy 3,2 10 4 , |
xy 1,3 10 3 . |
Требуется определить величину и направление |
|||
главных напряжений. Расчеты произвести при следующих исходных данных:
E2 105 МПа, 0,3 .
3.7.В окрестности точки заданы напряжения 1 50МПа; 2 30МПа;
3 40МПа.
1.Показать на гранях элемента, действующие напряжения,
2.Определить величину экстремальных напряжений 1 , 2 , 3 ,
3.Определить величину напряжений, действующих в плоскости, парал-
лельной оси 1, нормаль к которой составляет с осью 2 угол 60 .
4. Определить величину полного октаэдрического напряжения и его составляющих.
161
4.ВЫВОДЫ ПО РАЗДЕЛУ 10
1.Результатом взаимодействия выделенного параллелепипеда с остальным телом являются полные напряжения на гранях этого элемента, проекции
которых на координатные оси xx; yy ; zz ; xy; xz ; yz ; yx ; zx ; zy , полностью описывают напряженное состояние в точке и могут быть записаны в виде тензора напряжений Тн .
2. В силу закона парности напряжений тензор напряжений является симметричным, и описание напряженного состояния сводится к отысканию шести компонентов напряжений xx; yy ; zz ; xy; xz ; yz .
3.Три взаимно перпендикулярные площадки, на которых касательные напряжения отсутствуют, называются главными, а нормальные напряжения, действующие на этих площадках – главными напряжениями.
4.Значения главных напряжений при объемном напряженном состоянии
определяются из решения кубического уравнения 3 J1 2 J2 J3 0 . Между главными напряжениями должно выполняться соотношение 1 2 3 .
Коэффициенты и свободный член являются инвариантами напряженного состояния.
162
5. Частными случаями объемного напряженного состояния являются: плоское напряженное состояние, когда J3 0 и один из корней равен нулю, и
линейное – когда J2 J3 0 и два корня уравнения равны 0.
6. Максимальное касательное напряжение будет действовать на площадке параллельной главному напряжению 2 и равнонаклоненной к главным осям 1
и 2 и определяется по формуле max 1 3 .
2
7. В исследовании вопроса прочности материала наряду с главными плоскостями и плоскостями главных касательных напряжений, существенное значение имеют плоскости, пересекающие главные оси под одинаковыми углами, октаэдрические плоскости.
8.Для суждения о прочности в рассматриваемой точке, а так же для исследования законов деформации в окрестности той же точки разделяют компоненты напряжений, связанные только с объемной деформацией (шаровой тензор), от компонентов, связанных с изменением формы (тензор девиатор).
9.Исследование напряженного состояния в точке может производиться аналитически или графическим путем (круги Мора).
5.Совокупность деформаций, возникающих по разным осям и в различных плоскостях xx , yy , zz xy , xz , yz , проходящих через данную точку, определяет
деформированное состояние в рассматриваемой точке, и может быть записана в виде тензора деформаций.
11.Существуют три взаимно – перпендикулярные направления, по которым волокна или удлиняются, или укорачиваются. Они называются главными осями деформаций. Деформации в направлении главных осей называются главными деформациями и определяются при решении кубического уравнения
3 2 J1 J2 J3 0 .
12.Коэффициенты и свободный член являются инвариантами деформиро-
ванного состояния. Первый инвариант деформированного состояния равен относительному изменению объема.
13. Потенциальной энергии деформации U численно равна работе внешних сил А, совершаемой ими при упругой деформации, и рассматривается как сумма удельной потенциальной энергии изменения объема UV , и удельной по-
тенциальной энергии изменения формы Uф .
163
ЗАДАНИЯ К ВЫПОЛНЕНИЮ РГР
Расчетно-проектировочная работа №1 «Исследование объемного на- пряженно-деформированного состояния в точке»
Задание
С заданной точкой М связана система декартовых координат X, Y, Z. Расчетом определены координатные напряжения в этой точке xx , yy , zz ,
xy , |
xz , |
zy (табл. 1). Провести исследование напряженно- |
деформированного состояния детали в этой точке. Материал считать упругим, изотропным с механическими характеристиками: модулем упругости
E 2 105 МПа, коэффициентом Пуассона 0,3.
Требуется исследовать напряженно деформируемое состояние детали в точке в следующей последовательности:
1.Записать тензор напряжений в осях X, Y, Z. Изобразить в аксонометрии малый элемент, выделенный в окрестности точки М координатными сечениями и указать напряжения на гранях этого элемента.
2.Вычислить алгебраические инварианты тензора напряжений J1 ,
J2 , J3 . Определить с использованием ПЭВМ главные напряжения 1, 2 ,
164
3 , решая кубическое уравнение 3 - J1 2 J2 - J3 0 . Проверить пра-
вильность вычисления главных напряжений по выражению первого инварианта тензора напряжений J1 xx yy zz 1 2 3 . Записать тензор
напряжений в главных осях.
3.Определить главные напряжения 1, 2 , 3 , решая кубическое
уравнение 3 - J1 2 J2 - J3 0 .
4.Определить положение главных площадок.
5.Определить величину максимального касательного напряжения, предварительно указав положение площадки, на которой они развиваются.
6.Определить величины нормального и касательного напряжений на октаэдрической площадке, предварительно указав положение этой площадки.
7.Определить величины нормального и касательного напряжений на площадке, нормаль к которой образует углы 1 и 2 с первой и второй
главными осями напряжений.
8.Считая главные оси напряжений совпадающими с главными осями деформаций, определить из соотношений обобщенного закона Гука величины главных деформаций. Вычислить относительное изменение объема.
9.Разложить тензор напряжений в главных осях на шаровой тензор
итензор-девиатор.
10.Вычислить удельную потенциальную энергию изменения объема, энергию формоизменения, полную удельную потенциальную энергию упругой деформации.
11.Определить расчетные напряжения в заданной точке по гипотезе наибольших касательных напряжений.
12.Определить расчетные напряжения в заданной точке по гипотезе удельной потенциальной энергии формоизменения.
Пример 5.5.
Провести исследование напряженно-деформированного состояния детали в этой точке М при следующих исходных данных: xx = 8,40 МПа,
yy = -8,80 МПа, zz = -3,10 МПа, xy = 4,00 МПа, xz = 8,00 МПа, zy = 2,00
МПа.
1. Изобразим в аксонометрии параллелепипед, вырезанный в окрестности точки М, и покажем на его гранях напряжения
165
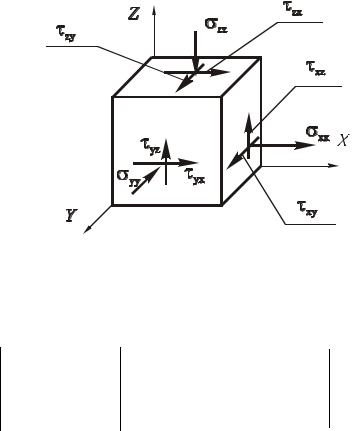
Рис. 5.34.
Схема распределения напряжений в окрестности точки М
Запишем тензор напряжений в осях X, Y, Z.
xx |
yx |
zx |
|
|
8,40 |
4,00 |
8,00 |
|
Тн xy |
yy |
zy |
|
; |
Тн 4,00 |
8,8 |
2,00 |
|
|
|
|||||||
xz |
yz |
|
|
|
8,00 |
2,00 |
3,1 |
|
zz |
|
|
||||||
2. Определим алгебраические инварианты тензора напряжений
J1 xx yy zz 8,40 8,80 3,10 3,50 МПа;
J2 xx yy zz yy xx zz xy2 zy2 xz2
8,40 8,80 8,80 3,10 8,40 3,10 4,002 8,002 2,002
156,68 МПа;
J2 xx yy zz 2 xy xz zy zz xy2 xx zy2 yy xz2
8,40 8,80 3,10 2 4,00 8,00 2,00 8,40 2,02 8,80 8,02 3,10 4,02
936,35 МПа.
3.Определяем значения главных напряжений
3 - J1 2 J2 - J3 0 ;
3 - 3,50 2 156,68 - 936,35 0.
Решая кубическое уравнение, находим 1 13,40 МПа, 2 7,20
МПа, 3 9,70 МПа.
Проверяем правильность решения кубического уравнения
J1 xx yy zz 1 2 3
13,40 7,20 9,70 3,50 J1 .
4.Определяем главные напряжения 1, 2 , 3 , решая кубическое
уравнение 3 - J1 2 J2 - J3 0 .
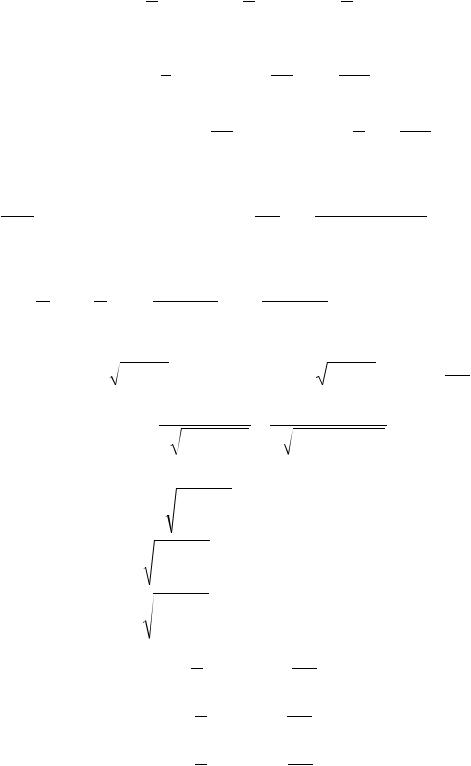
Представим уравнение в виде σ3 + aσ2 + σb + c = 0 ,
166
Где - a J1 |
3,50 |
МПа, |
b J2 156,68 |
МПа, c J3 936,35 |
|||||||||||||||||
МПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введя в рассмотрение выражение σ = r |
a / 3 , получим |
||||||||||||||||||||
|
|
|
|
a |
3 |
|
|
|
|
|
a 2 |
|
|
|
a |
c 0`, |
|
||||
|
r - |
3 |
|
a r - |
|
b r - |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
3 |
|
|
|
1 |
a |
2 |
|
|
|
|
2 |
a |
3 |
|
a b |
c |
|
|
||
|
|
3 |
|
b r |
27 |
|
3 |
|
0 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а с учетом обозначений |
p |
a2 |
b |
и |
|
|
|
a |
3 |
|
a b |
c , получим |
|||||||||
3 |
q 2 |
|
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||
r3 p r q 0.
p |
3,52 |
156,68 160,76 ; |
|
3,5 |
|
3 |
3,5 156,68 |
936,35 |
750,38 ; |
3 |
q 2 |
3 |
|
|
3 |
||||
|
|
|
|
|
|
|
r3 160,76 r 750,83 0;
p 3 |
q |
2 |
|
160,76 |
3 |
|
750,83 |
|
2 |
p 0 , ис- |
|
так как |
|
|
|
|
3 |
|
|
2 |
|
12939,32 0 и |
|
|
3 |
2 |
|
|
|
|
|
|
|
||
пользуем формулы
r1 2 |
p / 3 cos |
|
, |
r2,3 2 |
|
|
|
2 |
3 |
p / 3 cos |
3 |
, |
|||||
|
|
|
|
|
|
3 |
|
|
|
|
q |
|
2 |
750,38 |
|
|||
cos |
2 |
p / 3 3 |
160,76 / 3 3 0,956 . |
||||||||
|
|
|
|
|
17,06 , |
|
|
|
|||
|
r 2 |
|
|
160,76 cos 17,06 |
14,567 МПа, |
||||||
|
1 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r2 |
2 |
160,76 |
|
17,06 |
|
180 |
|
6,03 |
МПа, |
||
|
|
3 |
cos |
3 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
r3 |
2 |
160,76 |
|
17,06 |
|
180 |
|
8,54 |
МПа, |
||
|
|
3 |
cos |
3 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
1 r1 a3 14,567 33,5 13,4 МПа,
2 r2 a3 6,03 33,5 7,2 МПа,
3 r3 a3 8,54 33,5 9,7 МПа,
5.Определяем положение главных площадок
167
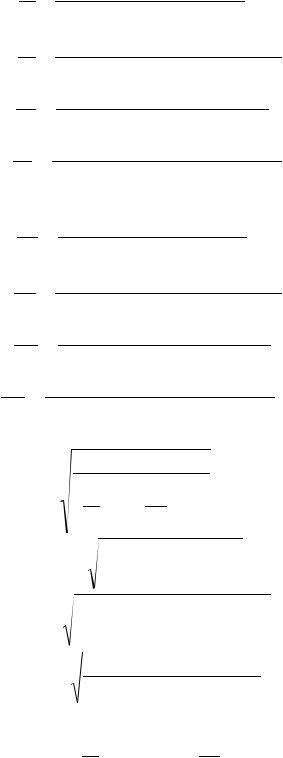
li ni
l1 n1 l2 n2 l3 n3
|
yy i zx zy yx |
где i 1,2,3; |
|
xy2 xx i yy i , |
|||
|
8,8 13,4 8,0 2,0 4,0 |
|
1,953; |
|
4,02 8,4 13,4 8,8 13,4 |
|
|
|
8,8 7,2 8,0 2,0 4,0 |
0,508 ; |
|
|
4,02 8,4 7,2 8,8 7,2 |
|
|
|
8,8 9,70 8,0 2,0 4,0 |
|
2,476 ; |
|
4,02 8,4 9,70 8,8 9,70 |
|
|
|
|
m |
xx i zy zx yx |
|
|
||||||||
|
|
i |
xy2 xx |
i yy i , |
где i 1,2,3; |
||||||||
|
|
ni |
|
||||||||||
|
|
m1 |
8,4 13,4 2,0 8,0 4,0 |
|
0,442; |
||||||||
|
|
n1 |
|
4,02 8,4 13,4 8,8 13,4 |
|
||||||||
|
|
m2 |
|
8,4 7,2 2,0 8,0 4,0 |
0,019 ; |
||||||||
|
|
n2 |
|
4,02 8,4 7,2 8,8 7,2 |
|
|
|||||||
|
|
m3 |
8,4 9,70 2,0 8,0 4,0 |
13,205; |
|||||||||
|
|
n3 |
|
4,02 8,4 9,70 8,8 9,70 |
|
|
|||||||
|
|
ni |
|
|
|
|
1 |
|
, |
где i 1,2,3; |
|||
|
|
l |
|
2 |
m 2 |
||||||||
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
1 |
|
0,447 ; |
||
|
|
|
|
1,9532 0,4422 |
|||||||||
|
|
|
|
|
|
1 |
|
|
|||||
|
|
n2 |
|
|
|
|
1 |
|
|
0,892; |
|||
|
|
0,508 2 |
0.019 2 1 |
||||||||||
|
|
|
n3 |
|
|
|
|
1 |
|
0,074. |
|||
|
|
|
2,4762 |
|
|
|
|||||||
|
|
|
|
|
13,205 2 1 |
|
|
||||||
Тогда направляющие косинусы li и mi определяются по формулам |
|||||||||||||
|
|
l |
|
n |
li |
|
и |
m |
n |
mi |
, где i 1,2,3; |
||
|
|
i |
i |
n |
|
|
i |
i |
n |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
m1 0,197 ; |
||
|
|
|
|
l1=0,873; |
|
|
|
||||||
|
|
|
|
l2 =-0,453; |
|
|
|
m2 0,017 ; |
|||||
|
|
|
|
l3 =0,184; |
|
|
m3 0,980 . |
||||||
Проверка: Сумма квадратов направляющих косинусов должна быть |
|||||||||||||
равна 1 - l 2 |
m 2 |
n |
2 |
1, где i 1,2,3. |
|
|
|
|
|||||
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8732 0,1972 |
0,4472 1. |
|||||||
168
