
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра
.pdf
19
где ij (i, j = 1,...,R) – перемещение точки приложения i-го силового фактора ( Xi ) по его направлению под действием единичного силового фактора с индексом j ( X j 1),
Xi (i = 1,…,R) – неизвестные усилия,
iP (i = 1,…,R) – перемещение точки приложения i-го силового фактора по
его направлению под действием всех заданных внешних сил.
Перемещения ij (i, j = 1,...,R) называются удельными перемещениями, так
как они вызываются единичными усилиями.
Удельные перемещения, имеющие одинаковые индексы, называются главными коэффициентами канонических уравнений. Они всегда положительны. Удельные перемещения с разными индексами называются побочными коэффициентами канонических уравнений. Они могут быть положительными, отрицательными или равными нулю.
Перемещения iP (i = 1,…,R) называются грузовыми членами канониче-
ских уравнений. Грузовые члены также как и побочные коэффициенты могут быть положительными, отрицательными или равными нулю.
Указанные перемещения ij и iP (i, j = 1,...,R) являются линейными, если Xi (i=1,…,R) представляет собой сосредоточенную силу, и угловыми – если
Xi (i=1,…,R) – момент.
Перемещения ij и iP (i, j = 1,...,R) для пространственного случая действия сил обычно определяют, записывая формулу Мора:
ij |
M xj M xi ds M yj M yi ds M кjM кi ds |
|||||||||||||||||||
S |
|
EIx |
|
|
S |
EI y |
|
S |
EIк |
|
|
|
(3) |
|||||||
kxQxjQxi ds kyQyjQyi |
|
|
|
|
|
|
|
|
|
|||||||||||
ds N j Ni ds, |
||||||||||||||||||||
S |
|
|
GF |
|
S |
GF |
|
S |
|
EF |
|
|
|
|
||||||
iP |
|
M |
xP |
M |
xi ds |
M yP M yi |
ds |
M |
кP |
M |
кi ds |
|||||||||
|
|
|
|
EI y |
|
|
|
|
||||||||||||
|
S |
|
|
EIx |
S |
|
S |
|
|
EIк |
|
(4) |
||||||||
|
k |
Q |
|
|
Q |
|
kyQyPQyi |
|
|
N |
|
N |
|
|||||||
|
xP |
xi ds |
ds |
|
P |
i |
ds, |
|||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
||||||||||
S |
|
|
GF |
S |
GF |
|
S |
|
EF |
|
|
|||||||||
где Е – модуль упругости, G – модуль сдвига,
I x , I y – моменты инерции поперечного сечения относительно главных осей, Iк – момент инерции поперечного сечения при кручении,
F – площадь поперечного сечения,
kx , k y – безразмерные коэффициенты, зависящие от геометрической формы поперечного сечения. Для прямоугольного сечения k kx ky 65 ,
20
для сплошного круглого сечения k 109 , для тонкостенного кру-
гового k 2.
Все стоящие под знаком интегралов обозначения с индексами j, i и P являются аналитическими выражениями внутренних силовых факторов (изгибающих и крутящих моментов, поперечных и продольных сил), возникающих под действием соответственно j-го, i-го единичных факторов и всех заданных внешних сил.
Вычисляя перемещения по формуле Мора, интегрирование производят по длине каждого участка, а суммирование – по всем участкам. При расчётах прямых брусьев дифференциал дуги ds заменяют величиной dz .
В выражениях (3), (4) не всегда все слагаемые являются равноценными. Для большинства встречающихся на практике рам и балок, где элементы работают на изгиб и кручение, три последних слагаемых в указанных выражениях оказываются существенно меньшими трёх первых. В этих случаях тремя последними интегралами, как правило, можно пренебречь. Тогда для плоской системы в формулах (3), (4) учитывают только одно первое слагаемое, учитывающее изгибающие моменты.
Вместе с тем, возможны такие случаи, когда все слагаемые оказываются величинами одного порядка.
При расчётах ферм – стержневых систем, элементы которых работают только на растяжение или сжатие, в выражениях (3), (4) учитывают только последнее слагаемое.
Если конструкция состоит из прямых участков и можно пользоваться правилом Верещагина, то ij (i, j = 1,...,R) представляет собой результат пере-
множения j-тых единичных эпюр на i-тые единичные эпюры. Единичной называют эпюру, построенную от действия соответствующего единичного силового фактора. Как известно, ij = ji (i, j = 1,...,R).
Величины перемещений iP (i = 1,...,R) определяют, перемножая эпюры
от заданных внешних сил (грузовые эпюры) на i-тые единичные эпюры.
В результате решения системы канонических уравнений (2) метода сил находятся величины усилий Xi (i = 1,…,R), после чего задача сводится к реше-
нию обычной статически определимой системы.
2. Использование свойств симметрии при раскрытии статической неопределимости
При расчёте симметричных статически неопределимых конструкций оказывается возможным упростить решение задачи и снизить число искомых силовых факторов.
Симметричной называется конструкция, у которой одна её часть может рассматриваться как зеркальное отображение другой части относительно плоскости симметрии (рис. 5).

21
Р
m

Плоскость симметрии
а)
РР

 m m
m m
Плоскость симметрии
б)
Р

 m
m
Рис. 5. Виды внешних нагрузок: а – симметричная нагрузка,
б– кососимметричная нагрузка.
Взависимости от расположения внешней нагрузки её делят на симметричную и кососимметричную. Симметричной называют такую нагрузку, при которой все внешние силы, приложенные к правой части рамы, являются зеркальным отображением сил, приложенных к левой части (рис. 5, а). Кососимметричной (или антисимметричной) называют такую нагрузку, при которой силы, приложенные к правой половине рамы, также являются зеркальным отображением сил, приложенных к левой половине, но противоположны им по знаку (рис. 5, б).
Внутренние силовые факторы классифицируются аналогично. Действующие в сечении С рамы (рис. 6) продольные силы X1 и изгибающие момен-
ты X3 относятся к симметричным, а поперечные силы X 2 |
- к кососимметрич- |
||||
ным силовым факторам. |
|
|
|
|
|
|
|
Х3 Х1 |
|
Х2 |
Х3 |
|
С |
|
Х1 |
||
|
|
||||
|
|
Х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а) |
б) |
Рис. 6. Симметричная статически неопределимая рама: а – схема рамы, б - внутренние силовые факторы в сечении С
Известно, что у симметричной конструкции в плоскости симметрии при симметричной внешней нагрузке обращаются в нуль кососимметричные сило-

22
вые факторы, а при кососимметричной внешней нагрузке – симметричные силовые факторы.
Для симметричной системы эпюры от кососимметричных факторов будут кососимметричны, а от симметричных факторов – симметричны (рис. 7).
Мизг 
 Мизг
Мизг
а) б)
Рис. 7. Эпюры изгибающих моментов: а - кососимметричная, б - симметричная
Перемножение кососимметричной эпюры на симметричную и наоборот даёт результат, равный нулю.
Независимо от вида и расположения внешней нагрузки для рамы (рис. 6, б) перемещения ij (i, j = 1, 2, 3), у которых один индекс принадлежит симмет-
ричному, а другой кососимметричному фактору, будут равны нулю. То есть,
12 =0, 23 =0.
Если нагрузка, приложенная к симметричной раме, не обладает ни прямой, ни косой симметрией, всегда имеется возможность разложить её на кососимметричную и симметричную, как показано, например, на рис. 8.
Р |
|
Р |
Р |
Р |
Р |
|
2 |
2 |
2 |
2 |
|
|
m |
m |
m |
m |
m |
|
2 |
2 |
2 |
2 |
|
|
|
Рис. 8. Разложение несимметричной нагрузки на кососимметричную и симметричную
В результате, задача распадается на две. Рассматривается отдельно симметричная рама с кососимметричной нагрузкой и рама с симметричной нагруз-

23
кой. Окончательно внутренние силовые факторы в раме определяются наложением полученных решений.
В случае если рама обладает, так называемой, косой геометрической симметрией (рис. 9, а), можно также путем сопоставления эпюр для двух половин рамы получить упрощения в системе канонических уравнений.
|
|
X1 |
|
|
|
C |
X3 |
X2 |
X3 |
Р |
Р |
Р |
X2 |
Р |
|
|
|
|
X1 |
а) |
б) |
|
в) |
|
Рис. 9. Выбор рациональной основной системы для рамы с косой геометрической симметрией: а - схема рамы, б - основная система, в - эквивалентная система
Например, при выбранной основной системе (рис. 9, б) 13 =0, 23 =0,1P =0, 2P =0, в чем нетрудно убедиться, рассмотрев внешний вид соответст-
вующих эпюр. В результате, сразу после записи системы канонических уравнений, можно сделать вывод о том, что X1 и X 2 равны нулю.
3. Определение перемещений в статически неопределимых системах
Для определения перемещений в статически неопределимой системе сначала следует раскрыть её статическую неопределимость и построить окончательную эпюру изгибающих моментов. Затем к интересующему нас сечению основной системы приложить единичную силу (или момент) в направлении предполагаемого перемещения и построить от её действия эпюру изгибающих моментов. При этом возможно использование как основной системы, уже выбранной ранее при раскрытии статической неопределимости, так и какой либо другой.
Как и прежде, при определении линейного перемещения к сечению прикладывается единичная сосредоточенная сила, при определении же углового перемещения (угла поворота сечения) – единичный момент.
Перемещение определяется перемножением окончательной эпюры изгибающих моментов на соответствующую единичную эпюру. Положительный результат перемножения говорит о том, что направление перемещения совпадает с направлением единичной силы (момента). Отрицательный результат говорит об обратном.

24
Конечно же, как уже говорилось выше, при невозможности применения правила Верещагина следует вычислять интеграл Мора аналитически, используя соответствующие выражения внутренних силовых факторов.
4. Расчёт многопролётных неразрезных балок с помощью уравнения трёх моментов
Неразрезными называют балки, лежащие более чем на двух опорах и не имеющие промежуточных шарниров. Такие балки являются статически неопределимыми. Обычно одна из опор для восприятия осевой нагрузки делается шарнирно-неподвижной или жёсткой заделкой.
Степень статической неопределимости неразрезных балок определяют как разность между количеством опорных реакций и количеством независимых уравнений статического равновесия. Отсюда следует, что если одна из опор является шарнирно-неподвижной, то число лишних связей равно числу промежуточных опор. Если одна из опор является жёсткой заделкой, то число лишних связей равно числу опор, исключая заделку.
Опоры неразрезных балок (рис. 10) принято нумеровать слева направо, обозначая крайнюю левую номером 0. Номер пролёта определяется номером принадлежащей ему правой опоры.
а)
б)
в)
|
P |
|
|
|
q |
|
|
|
|
|
|
|
Заданная |
0 |
|
1 |
|
2 |
3 |
система |
|
l1 |
|
l2 |
|
l3 |
|
|
|
|
|
|
|
Основная |
0 |
|
1 |
|
2 |
3 |
система |
|
P |
M |
|
M |
q |
|
|
|
1 |
|
2 |
|
Эквивалентная |
|
|
|
|
|
|
|
0 |
1 |
1 |
2 |
2 |
3 |
система |
Рис. 10. Многопролётная неразрезная балка: а - заданная система,
б– основная система, в - эквивалентная система
Сцелью упрощения решения выгодно выбирать основную систему врезанием в балку шарниров в сечениях над всеми промежуточными опорами (рис. 10, а) и в заделке (при наличии таковой). Лишними неизвестными в этом случае будут изгибающие моменты в опорных сечениях балки. При таком выборе основной системы действие заданной нагрузки распространяется только на тот пролёт, где она приложена.
Таким образом, эквивалентная система представляет собой ряд простых шарнирно опертых балок, нагруженных заданной пролётной нагрузкой и неизвестными изгибающими моментами, приложенными в сечениях, где были врезаны шарниры (рис. 10, в).

25
Очевидно, что взаимные угловые перемещения общих опорных сечений двух соседних балок будут равны нулю, так как в исходной балке эти два сечения образуют одно. Это утверждение справедливо для каждой опоры с номером n (рис. 11), где врезается шарнир.
а)
б)
в)
P |
q |
1 |
n-1
ln (lлев)
M |
(М ) |
P |
n-1 |
лев |
1 |
 n-1
n-1
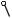 n-1
n-1
|
n |
|
|
n+1 |
|
|
||
|
|
|
|
ln+1 (lправ) |
|
|
|
|
M |
n |
(М ) |
q |
M |
n+1 |
(М |
) |
|
|
ср |
|
|
прав |
|
|||
n |
|
|
n |
n+1 |
|
n+1 |
|
|
левая |
средняя |
правая |
опора |
опора |
опора |
|
|
|
|
||||||
n |
лев. |
|
|
.n+1 |
прав |
||||
|
|
|
|
|
|
|
|
|
МР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
an (aлев) |
|
|
bn |
an+1 |
|
|
bn+1(bправ) |
||
|
|
||||||||
|
|
|
|||||||
|
|
|
|||||||
Рис. 11. Пара соседних пролётов неразрезной балки: а - заданная система, б - эквивалентная система, в - эпюра изгибающих моментов от пролётной нагрузки
Таким образом, каждое из уравнений (2) метода сил применительно к многопролётной неразрезной балке можно записать в следующем виде:
M |
l |
|
2M |
l |
|
|
l |
n 1 |
|
M |
l |
n 1 |
|
|
|
a |
|
|
|
b |
|
, (5) |
|||
n 1 I |
n |
|
I |
n |
I |
|
n 1 I |
6 |
I |
n |
l |
|
n |
I |
n 1 n 1 |
|
|||||||||
|
n |
|
|
n |
n |
|
n 1 |
|
|
n 1 |
|
|
n |
|
l |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n 1 n 1 |
|
|
|||||||
где M n 1, M n , M n 1 |
- опорные моменты на (n-1)-ой, |
n-ой и (n+1)-ой опоре |
|||||||||||||||||||||||
(рис. 11, б),
ln , ln 1 - длины n-го и (n+1)-го пролётов (рис. 11, а),
In , In 1 - моменты инерции поперечных сечений балки на n-ом и (n+1)-ом
пролётах,
n , n 1 - площади эпюр изгибающих моментов от заданной пролётной на-
грузки на n-ом и (n+1)-ом пролётах (рис. 11, в),
an , an 1 - расстояния от центров тяжестей площадей n и n 1 до левой
опоры своего пролёта,
bn , bn 1 - расстояния от центров тяжестей площадей n и n 1 до правой
опоры своего пролёта.
По числу опорных моментов, входящих в левую часть уравнения (5), его называют уравнением трёх моментов.
26
Для балок постоянного поперечного сечения (I = const) уравнение трёх моментов упрощается:
M n 1ln 2M n ln ln 1 M n 1ln 1 |
|
|
n |
a |
n |
|
|
b |
|
|
|
|
|
|
|
n 1 n 1 |
|
(6) |
|||
6 |
ln |
|
|
ln 1 |
. |
|||||
|
|
|
|
|
|
|
||||
Количество записываемых уравнений трёх моментов равно степени статической неопределимости балки, и их составляют для каждой опоры с врезанным шарниром.
Называя два соседних пролёта левым и правым, а опору в центре - средней, уравнение (6) можно переписать в виде:
|
левaлев |
|
|
|
|
b |
|
|
|
M левlлев 2Mср lлев lправ M правlправ 6 |
|
|
прав |
прав |
. (7) |
||||
|
l |
лев |
|
|
l |
прав |
|
|
|
|
|
|
|
|
|
|
|||
При составлении уравнения трёх моментов следует исключить член уравнения, содержащий момент над крайней шарнирной опорой, если со стороны этой опоры нет консоли (рис. 12, а). Если же консоль имеется, то входящий в составляемое уравнение момент над крайней опорой равен изгибающему моменту в этом сечении, определённому через внешнюю нагрузку, приложенную к консоли.
P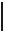
0 |
|
1 |
2 |
|
0 |
|
1 |
q |
|
l1 |
l2 |
|
l |
l=0 |
|
l1 |
l |
|
|
|
|
|
|
|
|
ql 2 |
M0 =0 |
|
M1 |
|
M2 = -Pl M=0 |
M0 |
|
|
M1 = 2 |
0 |
1 |
1 |
2 |
0 |
1 |
1 |
2 |
|
|
|
|
|
|
||||
|
|
а) |
|
|
|
|
б) |
|
Рис. 12. Статически неопределимые балки: а – с шарнирно-неподвижной опорой, б – с жёсткой заделкой
Если одна из опор является жёсткой заделкой, то её мысленно заменяют шарнирной опорой, добавляя при этом фиктивный пролёт нулевой длины (рис. 12, б). В этом случае рассматриваемая крайняя опора становится как бы промежуточной, и для неё также возможно записать уравнение трёх моментов.
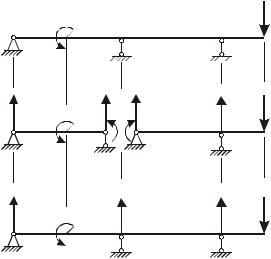
Решив систему уравнений трёх моментов, определяют значения всех опорных моментов. Затем определяют опорные реакции каждой двухопорной балки эквивалентной системы (рис. 13, б). Опорные реакции на промежуточных опорах неразрезной балки находят, складывая величины опорных реакций балок слева и справа от каждой опоры, как это показано на рис. 13, в. Построение эпюр поперечных сил и изгибающих моментов проводят обычным способом.
27
|
|
|
m |
|
|
|
P |
|
|
|
|
|
|
|
|
а) 0 |
|
|
|
1 |
|
2 |
|
|
R |
|
|
Rлев |
Rправ |
R |
P |
|
|
0 |
m |
1 M |
1 |
2 |
|
б) |
|
|
1 |
|
|
|
|
0 |
|
|
1 |
1 |
2 |
|
|
|
|
|
|
||||
|
R |
0 |
|
R1 = R1лев+ R1прав |
R |
P |
|
|
|
m |
|
|
2 |
||
в) |
|
|
|
|
|
|
|
0 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||
Рис. 13. Схема к определению опорных реакций неразрезной балки:
а– заданная система, б – эквивалентная система,
в– реакции неразрезной балки
5.Контроль правильности решения статически неопределимой системы
Окончательные эпюры внутренних силовых факторов подлежат обязательной проверке по условиям равновесия (статическая проверка) и по условиям неразрывности деформаций (деформационная проверка).
При статической проверке рассматривается равновесие какого-либо вырезанного узла или части системы. То есть, проверяется выполнение условий равенства нулю сумм проекций и моментов всех внешних и внутренних сил, приложенных к этой части:
Z 0, Y 0, mom 0.
При этом величины и направления внутренних силовых факторов, прикладываемых к отсечённой части, следует определять непосредственно по окончательным эпюрам.
Статическая проверка служит только для контроля правильности построения эпюр по найденным значениям лишних неизвестных усилий и не позволяет судить о правильности нахождения самих усилий. Следовательно, выполнение одной статической проверки – недостаточно.
При деформационной проверке определяют, соответствуют ли перемещения точек системы условиям опорных закреплений и неразрывности деформаций контура.
Взаданной статически неопределимой системе перемещение по направлению каждой из отброшенных лишних связей должно быть равно нулю. Следовательно, произведение окончательной эпюры изгибающих моментов на эпюру моментов любого единичного состояния основной системы также должно равняться нулю.
Вкачестве основной системы для единичного состояния лучше всего выбирать основную систему, отличную от уже использованной в расчёте. Количе-
28
ство деформационных проверок должно равняться числу лишних связей. Поскольку при расчётах статически неопределимых систем лишние неиз-
вестные вычисляются с определённой точностью, следовательно, и результаты проверок будут иметь некоторую погрешность. Поэтому при проверке следует отдельно вычислять сумму положительных и отрицательных членов. Если разница между этими суммами, выраженная в процентах к меньшей из них невелика (менее 5 %), то результаты расчёта можно признать верными.
2.КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Какая система называется статически неопределимой?
2.Что называют степенью статической неопределимости?
3.Что называют степенью свободы?
4.Сколько степеней свободы имеет свободное твёрдое тело на плоско-
сти?
5.Что такое связь, наложенная на тело?
6.Как определяют необходимое число связей.
7.Что называют лишней связью?
8.Что является причиной статической неопределимости системы?
9.Что называют внешней связью?
10.Что называют внутренней связью?
11.Может ли система быть статически неопределима и внешним и внутренним образом одновременно?
12.Что такое простой шарнир?
13.Как изменяет степень статической неопределимости системы врезание одиночного шарнира?
14.Как изменяет степень статической неопределимости системы врезание шарнира, соединяющего несколько стержней?
15.Как находится степень статической неопределимости и число лишних связей для сложных конструкций?
16.В чем заключается метод сил?
17. Чем обуславливается название расчёта: «метод сил»?
18.Что называется основной системой?
19.Может ли основная система быть статически неопределимой?
20.Должна ли основная система быть геометрически неизменяемой?
21.Какая система называется геометрически неизменяемой?
22.Сколько основных систем можно предложить для статически неопределимой системы?
23.Какие силовые факторы после выбора основной системы вводят в тех сечениях, где запрещены линейные перемещения?
24.Какие силовые факторы после выбора основной системы вводят в тех сечениях, где запрещены угловые перемещения?
