Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра

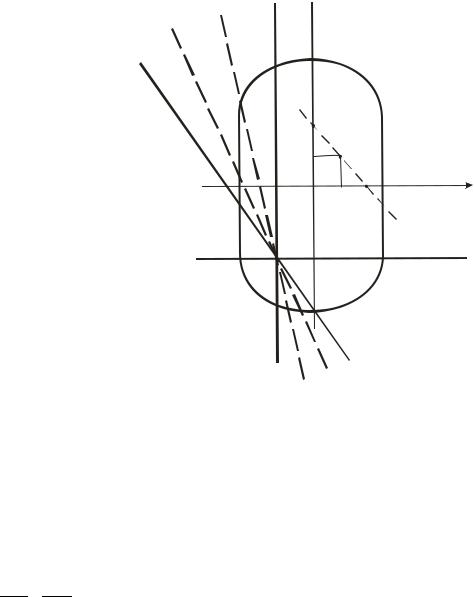
Существует еще одна важная зависимость между положением нулевой линии и соответствующей точкой приложения силы или так называемым полюсом нулевой линии: если нулевая линия вращается около некоторой определенной точки, лежащей на ней, то полюс (точка приложения силы) при этом перемещается по прямой.

Пусть, например, сила приложена в точке М(х0 , у0), и соответствующая нулевая линия n-n займет положение, показанное на рис.4.4.

n1 у

n

k

n1 n

Рис.4.4. Зависимость между положением нулевой линией и полюса при вращении нулевой линии около точки, лежащей на этой линии

Выберем на линии n-n произвольную точку С(х1 , у1) и, вращая около нее нулевую линию, проследим, как будут изменяться координаты полюса М. Так как нулевая линия при всех своих положениях проходит через постоянную точку С, то координаты последней (х1, у1) должны удовлетворять уравнению (4.4) нулевой линии. Подставив в это уравнение вместо текущих координат (х, у) координаты точки С, получим:

Равенство (4.7) можно рассматривать как уравнение прямой, в которой текущими координатами являются уже координаты полюса х0, у0. Следовательно, при вращении нулевой линии около точки С полюс М перемещается по прямой k-l, определяемой уравнением (4.7). Так как текущие

99

координаты х, у и координаты полюса х0, у0 входят в уравнение (4.4) совершенно равноправно, то справедливо и обратное положение, т.е. при перемещении полюса по прямой нулевая линия вращается около некоторой точки, лежащей на ней.

При положении полюса в точках М1 и М2 прямой k-l (рис.4.4), т.е. на осях х и у, нулевая линия займет соответственно положения n1-n1 и n2-n2 , пересечение которых определит центр ее вращения С. Действительно, при расположении полюса на одной из осей, отрезок, отсекаемый нулевой линией на другой оси, согласно выражениям (4.5) обращается в бесконечность, т.е. нулевая линия параллельна другой оси.

4.2. Ядро сечения.

При внецентренном сжатии брусьев, материал которых слабо сопротивляется растяжению, надо следить за тем, чтобы в сечении не появились растягивающие напряжения. Для этого нулевая линия должна проходить вне сечения или в предельном случае касаться сечения, не пересекая его (рис.4.3).

Оказывается, что для каждого поперечного сечения можно построить в его плоскости некоторый замкнутый контур, обладающий тем свойством, что при нахождении точки приложения продольной силы внутри или на границе этого контура в сечении возникают напряжения одного знака. Часть плоскости сечения, ограниченная этим контуром, носит название ядра сечения. При выходе сжимающей силы из ядра в сечении появляются растягивающие напряжения.

Для построения ядра сечения поступим следующим образом. Будем задавать положение нулевой линии так, чтобы она касалась сечения, нигде не пересекая его, и находить соответствующий полюс или точку приложения силы. При этом напряжения в сечении будут одного знака (рис.4.3). Проведя семейство касательных к сечению, мы получаем множество соответствующих им полюсов, геометрическое место которых дает очертание (контур) ядра сечения.

Если сечение имеет многоугольное очертание, то ядро сечения будет также многоугольником. Пусть, например, дано сечение, показанное на рис. 4.5, с главными осями х, у.

Для построения ядра сечения достаточно провести пять касательных к контуру сечения, из которых четыре совпадают со сторонами AB, AF, EF и ED, а пятая соединяет точки B и D. Проводить касательные, совпадающие со сторонами BC и CD, нельзя так как они пересекут сечение. Измерив или вычислив отрезки, отсекаемые указанными касательными 1-1, …, 5-5 на осях х и у , и, подставляя значения отрезков в формулы (4.6), определим координаты х0 , у0 для пяти полюсов 1, 2, …, 5, соответствующих пяти положениям

100

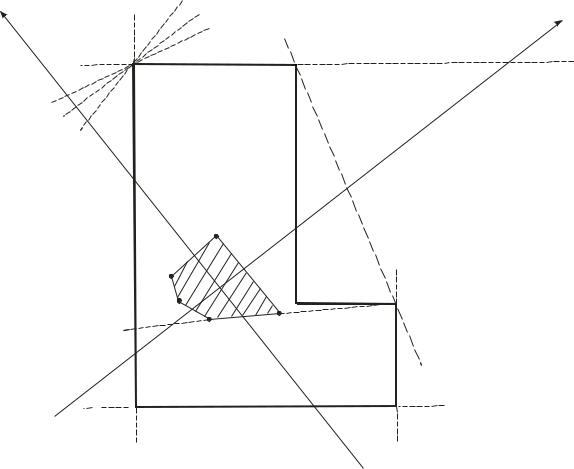
нулевой линии, и нанесем полюсы на чертеж. Касательную 1-1, которой соответствует полюс 1, можно перевести в положение 2-2, вращая ее около точки А. При этом полюс 1 согласно доказанной выше зависимости должен перемещаться по прямой и в результате поворота касательной оказаться в точке 2.

Следовательно, все полюсы, соответствующие промежуточным положениям касательной между 1-1 и 2-2, расположатся на прямой 1-2. Подобным же образом, переместив касательную 2-2 в положение 3-3 путем вращения ее около точки F , получим вторую сторону 2-3 ядра сечения и так далее. Отсюда видно, что ядро сечения будет многоугольником, для построения которого достаточно соединить полюсы 1,2,…, 5 прямыми.

1 2

Рис. 4.5. Ядро сечения для многоугольника

Если сечение (или часть его) имеет криволинейное очертание, то контур ядра (или соответствующей части его) будет тоже криволинейный.

101

Действительно, между двумя крайними касательными какого-либо участка кривой можно провести бесконечно множество промежуточных касательных, которые не пройдут через точку пересечения крайних касательных, а следовательно, и соответствующие им полюсы не могут лежать на одной прямой.

При построении ядра сечения отрезки, отсекаемые касательными к контуру сечения, удобно находить путем непосредственного измерения их на чертеже. Но при этом может оказаться, что точка пересечения касательной с главной осью выходит за пределы чертежа (например, точка пересечения касательной 5-5 и оси у на рис.4.5.). Обойти это затруднение можно, применяя иной способ построения ядра сечения.

Возьмем какую-либо вершину А сечения (рис.4.5.) и, определив ее координаты хА , уА , будем поворачивать вокруг нее нулевую линию. При этом полюс будет перемещаться по прямой, определяемой уравнением (4.7.). Отрезки, отсекаемые этой прямой на осях, будут:

При повороте нулевой линии из положения ВА в положение AF соответствующая часть траектории полюса 1-2 совпадает, конечно, с границей ядра сечения.

Нанеся прямую 1-2 на чертеж по отрезкам, повторим ту же операцию последовательно для всех остальных вершин сечения. Тогда совокупность пересекающихся прямых 1-2, 2-3, 3-4, … выделит ядро сечения. Точки пересечения этих прямых, т.е. вершины ядра, будут соответствовать совпадению нулевой линии со сторонами сечения.

Очевидно, что ядро сечения многоугольника будет также многоугольник, вершины которого суть полюсы, соответствующие нулевым линиям, совпадающим со сторонами многоугольника.

Для построения ядра сечения многоугольника следует:

1)найти главные центральные оси инерции и соответствующие радиусы инерции;

2)для каждой стороны найти отрезки a и b, отсекаемые ее продолжением на осях х и у;

3)вычислить координаты вершин ядра сечения по формулам (4.6.):

4) соединить вершины ядра прямыми.

102

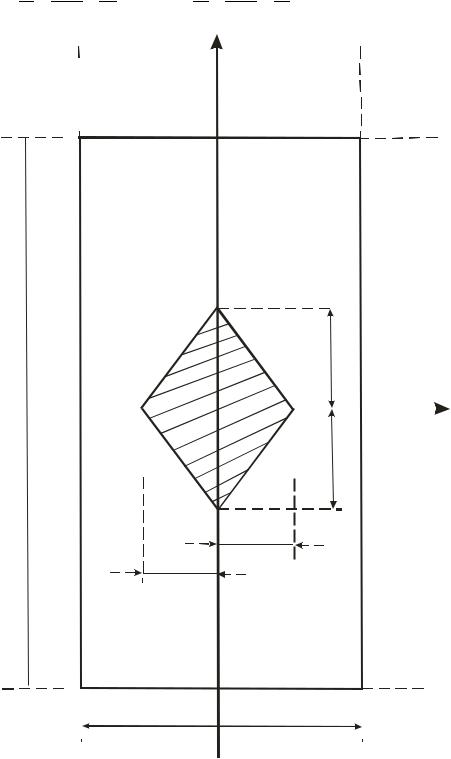
Частные случаи. Пример 4.1. Прямоугольное сечение (рис.4.6.).

К контуру прямоугольника можно провести четыре касательные, которые будут параллельны главным осям сечения, а потому соответствующие полосы будут расположены на главных осях.

Найдем вначале значения квадратов радиусов инерции:

1

b/6

b/6

Рис.4.6. Ядро сечения для прямоугольника

103

Задаемся четырьмя положениями нулевой линии, совпадающими со сторонами прямоугольника. Воспользовавшись формулами (4.8), получим:

для положения 1-1

Соединим полюсы 1, 2, 3,4 прямыми, получим изображенный на чертеже ромб, который и будет ядром сечения.

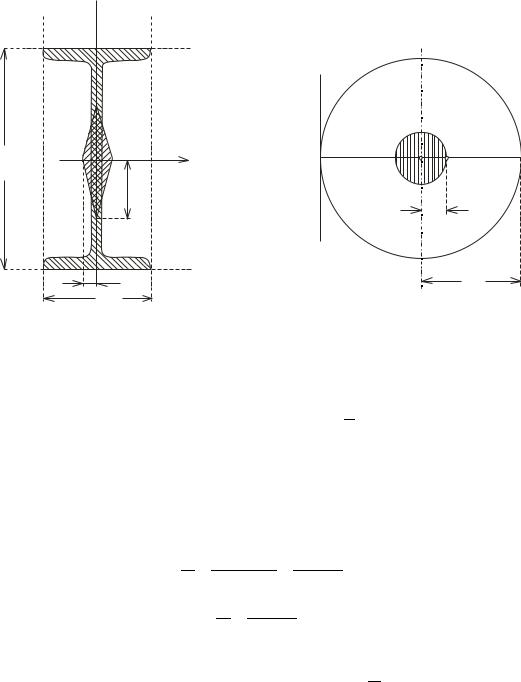
Пример 4.2. Двутавровое сечение (рис. 4.7). система касательных к сечению такая же, как и для прямоугольника, следовательно, ядро сечения имеет также форму ромба, полудиагонали которого e1 иe2 определяются из равенства (4.8):

r - радиус круга.

104

Отсюда радиус ядра сечения e1 i2 R2 r2 .

R 4R

Если внутренний радиус кольца увеличивается, стремясь к значению r R , то радиус e1 ядра сечения будет стремиться к значению R2 .

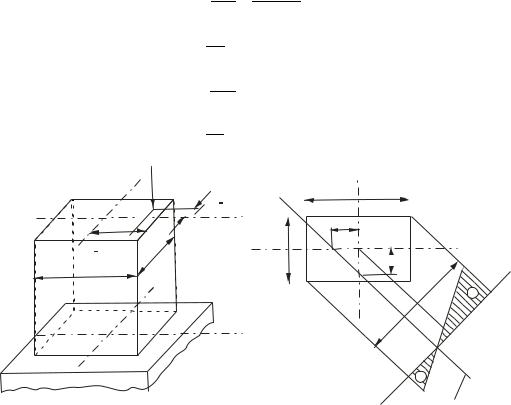
Пример 4.5. столб прямоугольного поперечного сечения (рис. 4.8, а) нагружен силой P, приложенной в точке А, координаты которой y0 5 см и

x0 12 см. найти положение нейтральной оси и построить эпюру нормальных

напряжений, возникающих в поперечном сечении столба. Собственным весом столба пренебречь.

Решение. Определяем геометрические характеристики сечения:

105

По формулам (4.3) определяем отрезки b и a, отсекаемые нейтральной осью на осях y и x:

b ix2 / y0 33,3/5 6,66 см; a iy2 / x0 75/12 6,25 см.

Определяем напряжение 0 в центре тяжести поперечного сечения (при y=0):

0 P / F 150 / 600 0,25 кН / см2 .

На рис. 4.8, б по полученным значениям b и a находим положение нейтральной оси nn. Перпендикулярно .той оси проводим прямую mm. Затем через центр тяжести сечения проводим линию, параллельную нейтральной оси, до пересечения в точке 7 с прямой mm. Из этой точки откладываем ординату 7- 8, равную напряжению 0 (в выбранном масштабе). Затем через точки 9

(пересечения нейтральной оси с прямой mm) и 8 проводим прямую, которая является линией, ограничивающей эпюру напряжений .

Пример 4.6. Построить ядро сечения для поперечного сечения в виде тавра, изображенного на рис. 4.9.

106

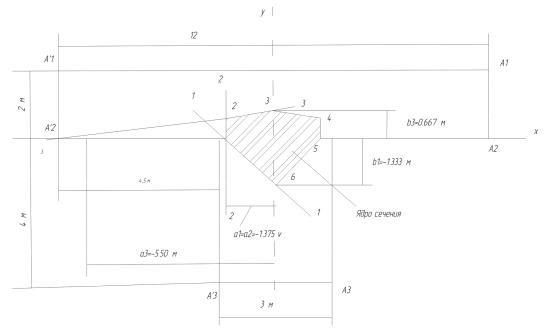
Ядро сечения для двутавра

Центр тяжести сечения находится в точке О. Геометрические характеристики сечения: F 36 м2 , J x 96 м4 , J y м4 .

Решение. При полюсе в точке A1 (с координатами YA1 2м и XA1 6м) отрезки, отсекаемые нулевой линией на осях координат, равны:

b1 ix2 /YA1 Jx / FYA1 96 /(36 2) 1,333м;

a1 iy2 / XA1 Jy / FXA1 297 /(36 6) 1,375м.

По значениям этих отрезков на рис. 4.9. построена нулевая линия 1-1. При

По этим значениям отрезков построена нулевая линия 3-3. Нулевые линии при полюсах в вершинах A1, A2 , A3 многоугольника, строим, используя

симметрию сечения относительно оси y. Многоугольник 1-2-3-4-5-6,

107

образованный построенными нулевыми линиями, представляет собой ядро сечения (рис. 4.9).

2.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какое сложное сопротивление называется внецентренным растяжением (или сжатием)?

2.какие внецентренно растянутые (или сжатые) брусья называются жесткими и какие гибкими?

3.По каким формулам определяются нормальные напряжения в поперечных сечениях бруса при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений? Выведете соответствующие формулы.

4.Как определяется положение нейтральной оси при внецентренном растяжении и сжатии? Выведете соответствующие формулы.

5.Как перемещается нейтральная ось, когда координата Y0 полюса

возрастает по абсолютной величине?

6.Чему равно нормальное напряжение в центре тяжести поперечного сечения при внецентренном растяжении и сжатии?

7.Какой вид имеет формула нормальных напряжений и как расположена нейтральная ось в случае, когда полюс находится на одной из главных центральных осей инерции сечения?

8.С помощью какой эпюры наиболее удобно можно определить нормальные напряжения в любой точке поперечного сечения?

9.Что называется ядром сечения?

10.Как строится ядро сечения?

108