3.2.3. Построение полной развертки усеченной части конуса.

Полная развертка усеченной части конуса т. е. части, находящейся за секущей плоскостью состоит из развертки боковой поверхности, к которой присоединяют натуральные величины сечения и основания конуса (рис. 241).

Развертка боковой поверхности конуса в данном примере представляет собой сектор круга, радиус которого равен образующей прямого кругового конуса. Угол сектора определяется по формуле:

φ = (R/L) ∙ 360

где R – радиус окружности основания конуса,

L – длина образующей конуса.

Для нанесения на развертку линии сечения делят дугу сектора на 12 частей и проводят образующие 1-S; 2-S;... 12S; на фронтальных проекциях точек (I₄; II₄; III₄ ...) проводят прямые, параллельные основанию конуса, до пересечения с контурной образующей 12₄S₄, что равносильно повороту образующих в положение, при котором они будут параллельными плоскости П₄. Полученные точки (I₄’; II₄’; III₄’ ...) с контурной образующей переносят на соответствующие образующие развертки (SI = S₄I₄’; SII = S₄II₄’...).

На практике построение боковой поверхности развертки конуса заменяется разверткой правильной двенадцатигранной пирамиды, вписанной в заданный конус, тогда не вычисляя величину угла φ, можно определить длину дуги сектора путем откладывания на нее 12 раз хорды, стягивающей 1/12 часть окружности основания конуса

(1₁-2₁ = 1 -2 = 2-3 = ...)

На рис. 241 показана полная развертка усеченного конуса с помощью 12 образующих, замененных ребрами двенадцатигранной правильной пирамиды.

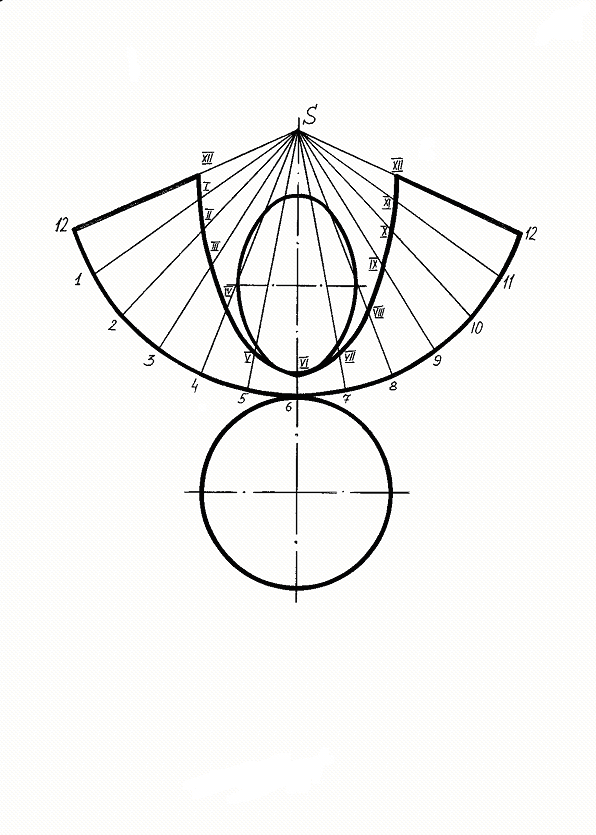
Рис. 241

В заключение следует отметить, следующее:

1) Если секущая плоскость проходит через вершину конуса, то она пересекает боковую поверхность его по двум образующим (прямым линиям);

2) Если секущая плоскость не проходит через вершину конуса и пересекает все образующие одной полости поверхности, или, иначе, не параллельна ни одной из образующих конуса, то в пересечении получается эллипс или часть эллипса; в этом случае угол между секущей плоскостью и осью конуса больше угла между этой осью и образующей конуса (на рис. 240 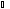α будет больше 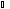β);

3) Если секущая плоскость параллельна только одной из образующих конуса, то в сечении получается парабола (в этом случае на рис. 240 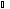α будет равен 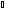β);

4) Если секущая плоскость параллельна двум образующим конуса, то в сечении получается гипербола (в этом случае на рис. 240 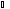α будет меньше 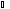β):

5) Если секущая плоскость перпендикулярна к оси конуса вращения, то в сечении получается окружность.

Кривые линии, получаемые от пересечения поверхности конуса второго порядка различными плоскостями – эллипс, парабола, гипербола и окружность, называются коническими сечениями.

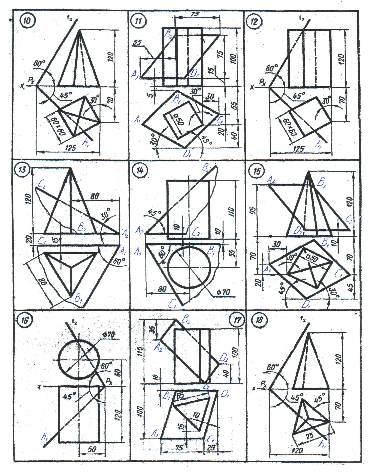
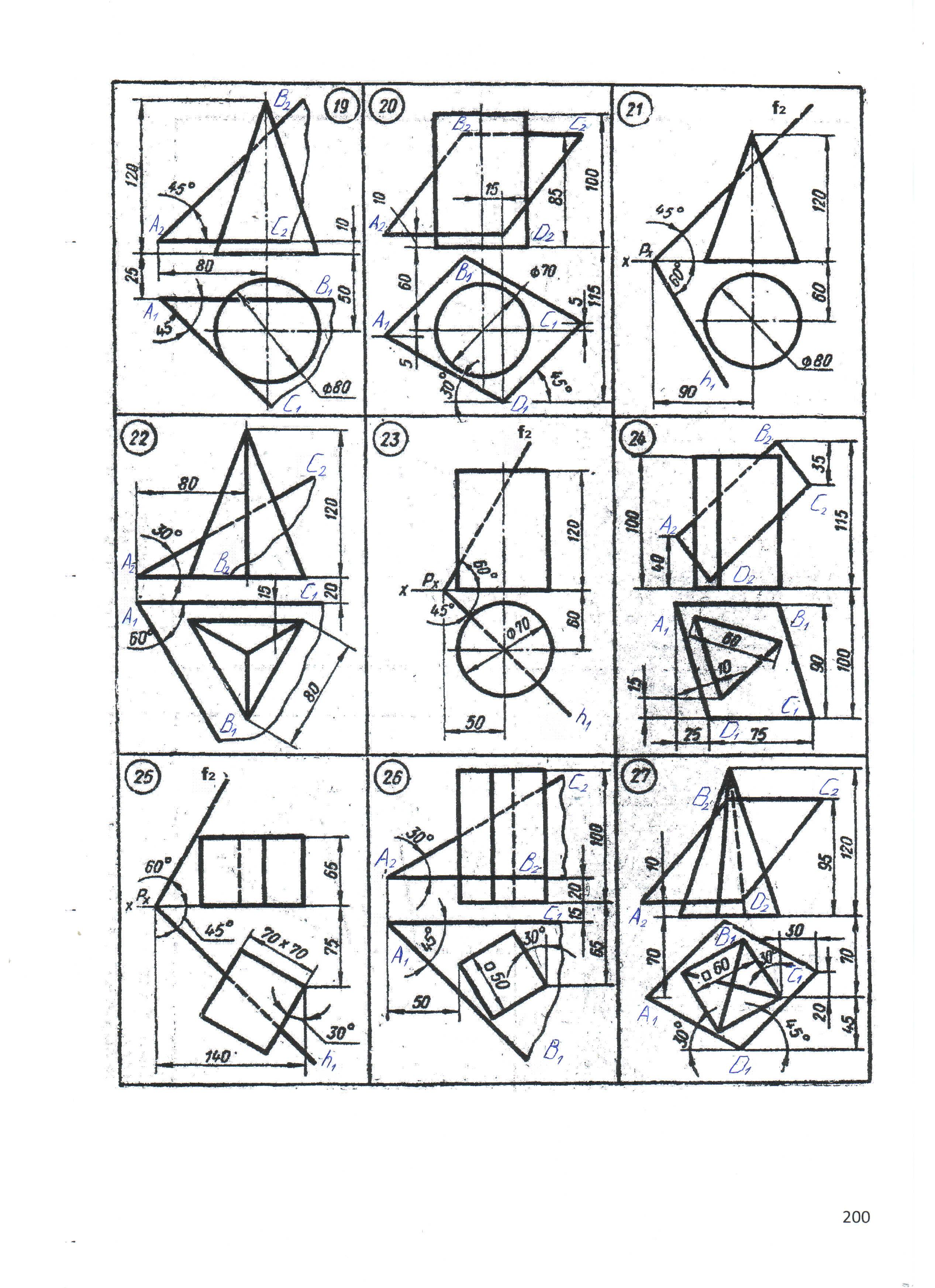
3.2.4. Варианты заданий (эпюр №2).

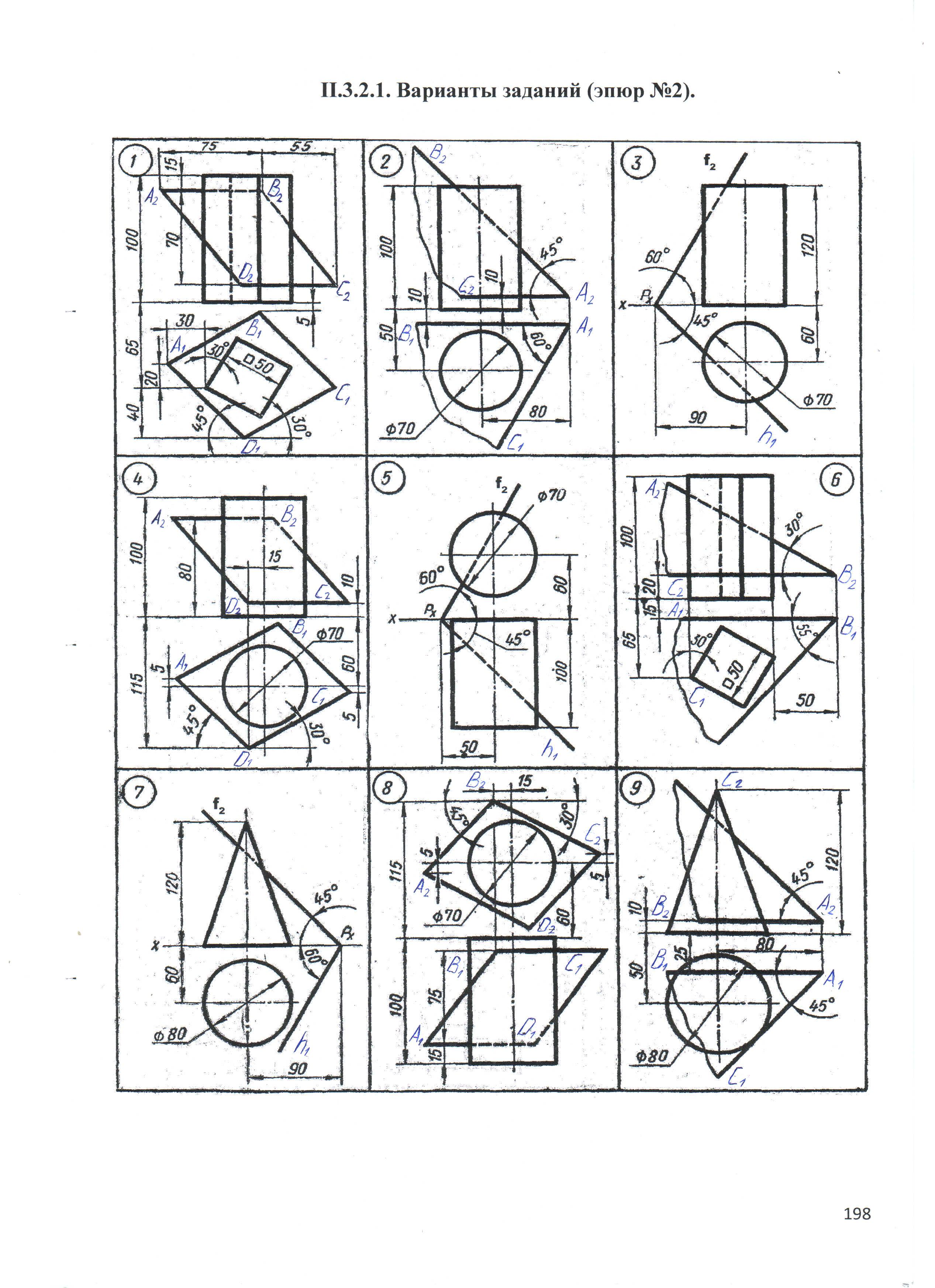
3.2.5. Образец выполнения эпюра №2.

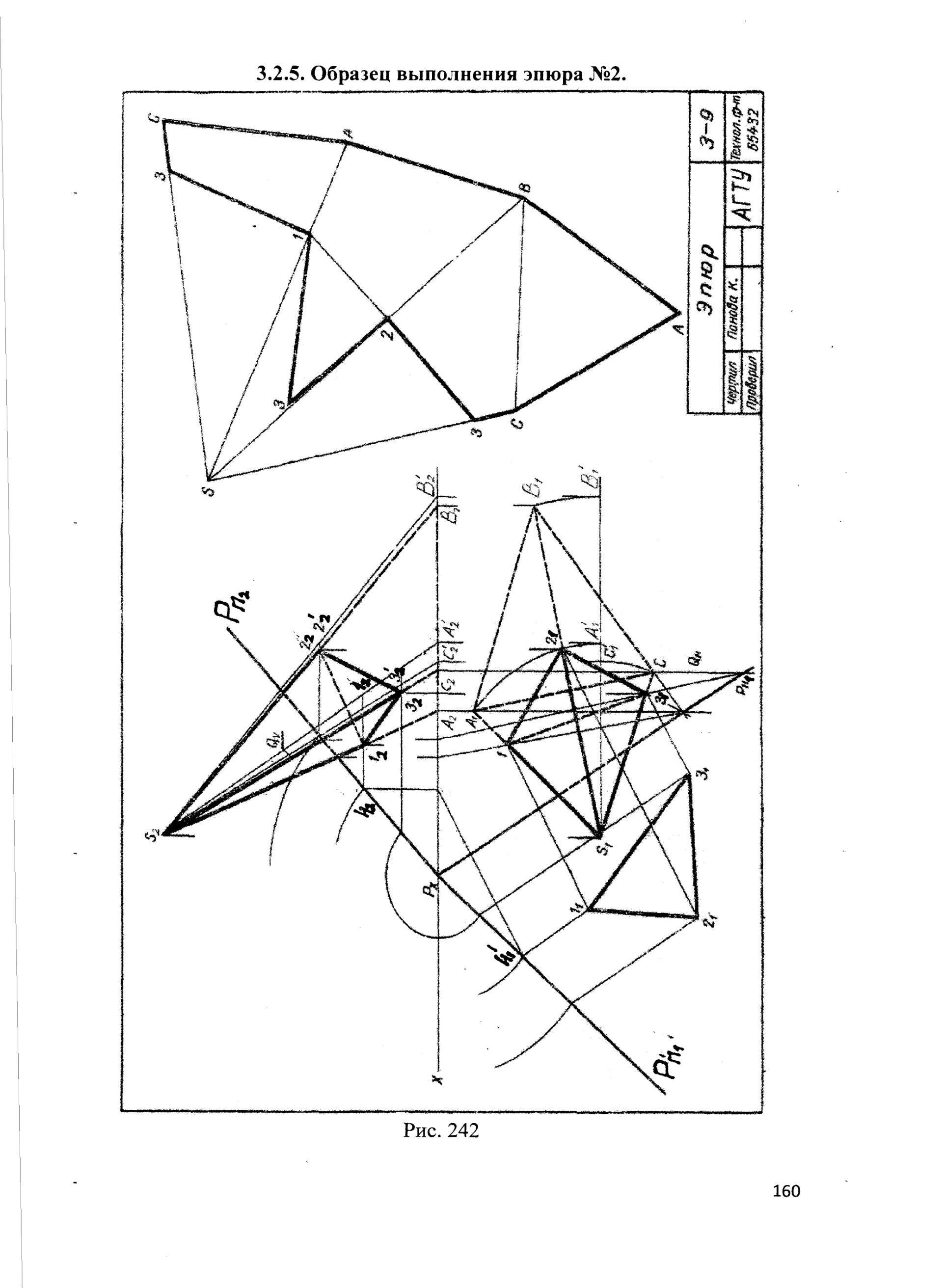
Рис. 242

3.2.6. Контрольные вопросы (эпюр №2).

1. Что называется многогранником?

2. Что называется пирамидой, призмой?

3. В чем состоит алгоритм построения линии пересечения многогранника с плоскостью общего положения?

4. Как найти натуральную величину сечения многогранника плоскостью?

5. Что называется разверткой многогранной поверхности?

6. К чему сводится построение развертки многогранника?

7. Что называется поверхностью вращения?

8. Какие поверхности вращения называются поверхностями вращения второго порядка?

9. Укажите общую схему определения линии пересечения кривой поверхности плоскостью?

10. Какие точки линии пересечения поверхности плоскостью называются главными (опорными)?

11. Укажите условия, при которых в сечении конуса вращения плоскостью получается окружность, эллипс, парабола, пересекающиеся прямые?

12. Что называется разверткой поверхности?

13. Какие поверхности называются развертывающимися и какие неразвертывающимися?

14. Укажите основные свойства разверток.

15. Что является разверткой цилиндра вращения и конуса вращения?

16. Как соединить кратчайшим путем две точки, лежащие на поверхностях цилиндра вращения и конуса вращения?