3.2. План решения задачи №1.
3.2.1. Сечение многогранника плоскостью.
Задача построения сечения многогранной поверхности плоскости сводится к последовательному определению точек пересечения ребер заданного тела с секущей плоскостью (первый способ) или к построению линий пересечения граней многогранника с секущей плоскостью (второй способ).
Выбор того или иного способа построения проекций сечения многогранника плоскостью зависит от положения заданного геометрического тела относительно плоскостей проекций и секущей плоскости,
Пример №1. Построить сечение трехгранной прямой призмы плоскостью общего положения, заданной пересекающимися прямыми (фронталью и горизонталью) f ∩ h (рис. 236 и 237).
В данном примере многогранник расположен таким образом, что его нижнее основание находится в плоскости П1, а боковые грани являются горизонтально – проецирующими плоскостями, поэтому горизонтальные проекции (I1; II1; III1) точек сечения определяются без построений и образуют треугольник.
Фронтальная проекция линии сечения II-III (II2-III2) представляет собой линию пересечения грани призмы СВС′В' с секущей плоскостью (f ∩ h). Для ее построения использована вспомогательная горизонтально – проецирующая плоскость Q (Q1) (второй способ).
Для нахождения фронтальной проекции точки I (I1) сечения, где ребро АА´ призмы пересекает плоскость (f ∩ h), использована вспомогательная горизонтально – проецирующая плоскость Δ(Δ1), как показано на рис. 237; таким образом точки I2, II2, III2 образуют фронтальную проекцию сечения, а точки I1, II1, III1 – горизонтальную проекцию.
Для построения полной развертки усеченной призмы необходимо знать истинные размеры боковых ребер, размеры оснований призмы и наклонного сечения (I, II, III). В данном примере основание призмы проецируется на горизонтальную плоскость проекций в натуральную величину. Фронтальные проекции боковых ребер являются также натуральными величинами ребер.
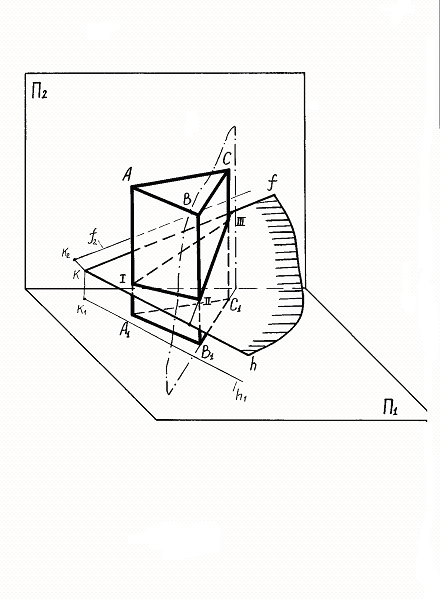
Рис. 236
Для определения истинной величины наклонного сечения I, II, III выбран способ перемены плоскостей проекций, где сечение в системе плоскостей П1/П4 займет положение фронтально-проецирующей плоскости, а после второй замены - в системе П4/П5 - положение горизонтальной плоскости уровня, тогда проекция треугольника сечения (I5, II5, III5) будет истинной величиной сечения.
Построение новой фронтальной проекции сечения в системе П1/П4 показано на рис. 237, новая ось х14 проекций проведена перпендикулярно горизонтальной проекции hi горизонтали, т.е. х14 ┴ hi, тогда проекция сечения (I4, II4, III4) представляет собой отрезок прямой. Затем для определения натуральной величины треугольника сечения используется вторая замена плоскостей проекций (см. рис. 237). Новая плоскость проекций П5 параллельна I4, II4, III4, поэтому ось проекций X45 ║ I4, II4, III4 , а проекция треугольника сечения (I5, II5, III5) в новой системе плоскостей проекций П4/П5 - есть истинная величина.
На рис. 238 показано построение развертки призмы. На горизонтальной прямой от произвольной точки отложены отрезки АВ, ВС, СА, которые равны длинам сторон основания призмы. Далее из точек А, В, С восстанавливают перпендикуляры и на них откладывают высоты точек I, II, III (отрезки А2I2, B2II2, C2III2); получают соответственно точки I, II, III ломаной линии сечения.
Получив развертку усеченной боковой поверхности, пристраивают к ней основание призмы и натуральную величину сечения треугольника с вершинами (I, II, III).
В соответствии с ГОСТ 2.303-68 линии сгиба на развертке показаны сплошными тонкими линиями толщиной от S/3 до S/2.
Рис. 237
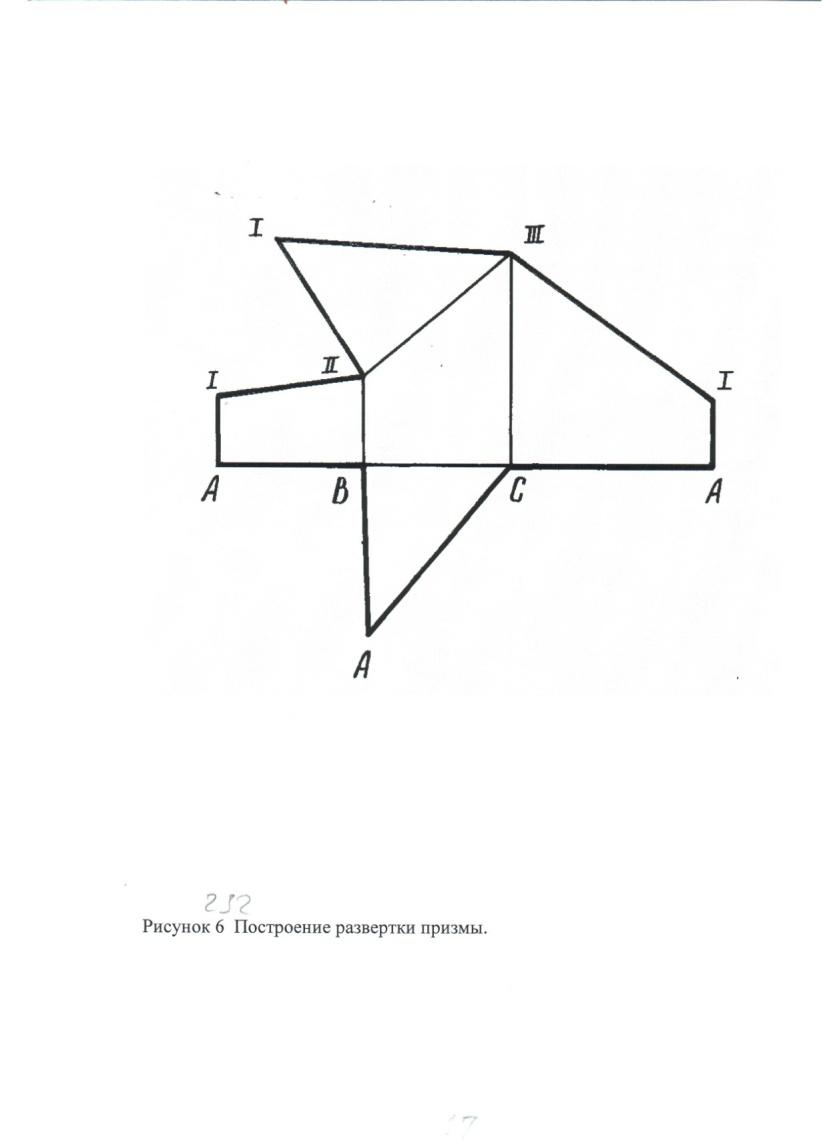
Рис. 238