7.4.Развертки поверхностей
109. Дан тетраэдр SАВС и две точки M и N (рис. 216). Построить кратчайшую линию на поверхности тетраэдра SАВС, соединяющую точки M и N, если точка М на фронтальной проекции видима.
Рис. 216
110. Построить развертку поверхности призмы и определить на ней положение отрезка MN (M1N1) (рис. 217).
Рис. 217
111. Построить развёртку треугольной пирамиды DABC (рис. 218).
Рис. 218
Решение
Так как развёрткой многогранника является плоская фигура, полученная последовательным совмещением с плоскостью одной грани всех остальных граней, то задача сводится к нахождению натуральных величин граней DAB, DBC, DCA, ABC, что в свою очередь сводится к нахождению натуральных величин рёбер DA, DB и т.д. Определить натуральных длину ребра можно любым из рассматриваемых выше способов. Затем, пристраивая один треугольник к другому с помощью засечек циркуля, строим развёртку пирамиды (рис. 219).
На развёртке вершины 5, 6, 8 и т.д. пространственной ломаной линии находим с помощью засечек на натуральных величинах рёбер или прямых, на которых они лежат.
Рис. 219
112. Построить пирамиду SАВС по заданной ее развертке, если основание АВС параллельно плоскости П1 (Рис. 220).
Рис. 220
113. Построить развертку поверхности усеченного конуса (рис. 221).
Рис. 221
114. Построить развертку конической части трубы (рис. 222).
Рис. 222
115. По заданной развертке цилиндрической поверхности вращения (рис. 223) построить ее ортогональные проекции, расположив ось перпендикулярно плоскости П1.
Рис. 223
116. Построить развертку вытяжной трубы (рис. 224).
Рис. 224
8. Задачи к теме: «Аксонометрические проекции»
117. Построить прямоугольную изометрическую и диметрическую проекции точек: А (20;30;40), В (50;20;0), С (0;30;30).
118. Построить прямоугольную изометрическую и диметрическую проекции отрезка АВ прямой линии, заданной координатами точек А (60;50;10) и В (20;20;40).
119.
Построить
прямоугольную изометрическую и
диметрическую проекции
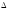АВС,
заданного своим комплексным чертежом
(рис. 225).
Рис. 225
120. Построить стандартные ортогональные изометрию и диметрию, а также косоугольную фронтальную диметрическую проекцию плоских фигур, заданных своими эпюрами (рис. 226).
Рис. 226
121. Построить стандартные прямоугольные изометрическую и диметрическую проекции и косоугольную фронтальную диметрическую проекцию правильной треугольной пирамиды и шестиугольной призмы, заданных своими эпюрами (рис. 227, рис. 228).
Рис. 227 Рис. 228
122. Построить стандартные прямоугольные изометрическую и диметрическую проекции окружностей радиусом 60 мм, расположенных в плоскостях проекций с центрами в точках: А (60; 100; 0); В (90; 0; 70) и С (0; 90; 100).
123. Построить стандартные прямоугольные изометрию и диметрию, а также косоугольную горизонтальную изометрию конуса вращения и цилиндра вращения, заданных своими комплексными чертежами (рис. 229, рис. 230).
Рис. 229 Рис. 230
124. Построить все стандартные аксонометрические проекции детали, заданной ее комплексным чертежом (рис. 231).
Рис. 231