
- •М.М. Харах
- •Предисловие
- •Условные обозначения
- •Введение.
- •Предмет начертательной геометрии.
- •Центральная и параллельная проекции.
- •Свойства параллельной проекции.
- •Комплексный чертеж точки, прямой линии и плоской фигуры.
- •Ортогональное проецирование. Эпюр Монжа.
- •Связь между прямоугольными проекциями точки и ее ортогональными координатами.
- •Прямая линия. Плоскости.
- •Задание и изображение прямой.
- •Задание и изображение плоскости.
- •Прямые и плоскости частного положения.
- •Проецирующие прямая и плоскость.
- •Прямые и плоскости уровня.
- •Многогранники.
- •Основные понятия и определения. Изображение многогранников на чертеже.
- •Кривые линии и их проекционные свойства.
- •Основные понятия и определения.
- •Пространственные кривые линии.
- •Цилиндрическая винтовая линия.
- •Обводы.
- •Алгоритм построения обвода из дуг окружностей.
- •Алгоритм построения обводов из дуг кривых второго порядка.
- •Кривые поверхности. Их образование и задание на чертеже. Основные понятия и определения.
- •Очертание поверхности.
- •Систематизация поверхностей.
- •Поверхности вращения.
- •Построение главного медиана поверхности вращения.
- •Поверхности вращения второго порядка.
- •Развертывающиеся линейчатые поверхности.
- •Линейчатые поверхности с плоскостью параллелизма.
- •Винтовые поверхности.
- •Прямой геликоид.
- •Наклонный геликоид.
- •Способы преобразования комплексного чертежа.
- •Способ замены плоскостей проекций.
- •Вращение.
- •Вращение вокруг проецирующей прямой.
- •Вращение вокруг линии уровня.
- •Вращение без указания оси вращения. (Способ плоскопараллельного движения).
- •Позиционные задачи.
- •Первая основная позиционная задача.
- •Пересечение двух плоскостей.
- •Пересечение многогранника плоскостью.
- •Пересечение прямой с поверхностью многогранника.
- •Взаимное пересечение многогранников.
- •7.6. Пересечение кривой поверхности плоскостью.
- •7.7. Пересечение прямой линии с кривой поверхностью.
- •7.8. Взаимное пересечение кривых поверхностей.
- •7.8.1. Способ вспомогательных секущих плоскостей.
- •7.8.2. Способ вспомогательных секущих сфер.
- •7.8.2.1. Способ концентрических сфер.
- •7.8.2.2. Способ эксцентрических сфер.
- •Вопросы для самопроверки.
- •Метрические задачи.
- •Определение натуральной величины отрезка прямой способом прямоугольного треугольника.
- •Перпендикулярность двух прямых, прямой и плоскости.
- •Развертки поверхностей.
- •Развертки многогранников.
- •8.3.2. Построение приближенных разверток развертывающихся поверхностей.
- •8.3.3. Условные развертки неразвертывающихся поверхностей.
- •8.3.4. Построение развертки методом нормального сечения.
- •8.3.5.Построение развертки методом раскатки.
- •8.3.6. Применение разверток в технике.
- •Вопросы для самопроверки.
- •9. Аксонометрические проекции.
- •9.1. Основные понятия и определения.
- •9.2. Основная теорема аксонометрии (теорема Польке).
- •9.3. Прямоугольная аксонометрическая проекция и ее свойства.
- •9.4. Стандартные аксонометрические системы.
- •9.5. Прямоугольная диметрия.
- •9.6. Изображение окружности в ортогональной аксонометрии.
- •9.7.Косоугольные аксонометрические проекции.
- •9.8. Построение аксонометрической проекции фигуры, заданной ее комплексным чертежом.
- •Приложение I. Задачи по начертательной геометрии.
- •1. Задачи к теме: «Точка, прямая, плоскость»
- •1.1. Центральные и параллельные проекции.
- •1.2. Прямоугольные проекции.
- •1.2.1. Точка на чертеже Монжа.
- •1.2.2. Прямая линия.
- •1.2.3. Плоскость
- •2. Упражнения и задачи к теме: «Кривые поверхности. Точка на поверхности»
- •3. Задачи к теме: «Способы преобразования»
- •3.1. Способ замены плоскостей проекций.
- •3.2 Вращение вокруг проецирующей прямой
- •3.3 Вращение вокруг линии уровня.
- •3.4 Плоскопараллельное движение
- •3.5 Применение способов преобразования комплексного чертежа
- •4. Позиционные задачи
- •5.Многогранники. Позиционные задачи на многогранники
- •Кривые поверхности.
- •6.2. Пересечение кривой поверхности с прямой линией.
- •6.3. Взаимное пересечение кривых поверхностей.
- •6.3.1. Способ секущих плоскостей.
- •6.3.2. Способ концентрических сфер.
- •6.3.3. Способ эксцентрических сфер.
- •7. Метрические задачи
- •7.1. Определение натуральной величины отрезка прямой.
- •7.2. Перпендикулярность прямых.
- •7.3. Перпендикулярность прямой и плоскости.
- •7.4.Развертки поверхностей
- •8. Задачи к теме: «Аксонометрические проекции»
- •Приложение II Графические задания.
- •1. Методические указания по выполнению заданий.
- •1.1. Общие требования.
- •1.2. Порядок сдачи заданий.
- •2. Задание 1 (эпюр №1). Тема: «Точка, прямая, плоскость. Позиционные и метрические задачи».
- •2.1. Указания по выполнению задания.
- •2.1.1. План решения задачи №1.
- •2.1.2. План решения задачи №2.
- •2.1.3. План решения задачи №3.
- •2.2. Варианты задания (эпюр №1).
- •2.3. Контрольные вопросы (эпюр №1).
- •3. Задание 2 (эпюр №2).
- •3.2. План решения задачи №1.
- •3.2.1. Сечение многогранника плоскостью.
- •3.2.2. Пересечение поверхности вращения плоскостью.
- •3.2.3. Построение полной развертки усеченной части конуса.
- •3.2.4. Варианты заданий (эпюр №2).
- •3.2.5. Образец выполнения эпюра №2.
- •3.2.6. Контрольные вопросы (эпюр №2).
- •4. Задание 3 (эпюр №3). Тема: «Взаимное пересечение кривых поверхностей методом вспомогательных секущих плоскостей и вспомогательных секущих сфер».
- •4.1. Указания по выполнению задания.
- •4.1.1. Указания к оформлению.
- •4.2. Способ секущих плоскостей.
- •4.3. Следствие из вспомогательной теоремы.
- •4.4. Способ вспомогательных секущих сфер.
- •Варианты заданий на способ
- •Приложение III Тесты Тест № 1: «Комплексный чертеж точки»
- •Тест №2: «Комплексный чертеж прямых общего и частного положения»
- •Тест №3: «Взаимное положение двух прямых»
- •Тест №4: «Комплексный чертеж плоскости общего и частного положения»
- •Тест №5: «Многогранники»
- •Тест №6: «Многогранники. Точка и прямая на поверхности»
- •Тест №7: «Кривые поверхности»
- •Тест №8: «Точка на поверхности»
- •Тест №9: «Способ замены плоскостей проекций»
- •Тест №10: «Способ вращения вокруг проецирующей прямой»
- •1 2 3
- •Тест №12: «Пересечение многогранника плоскостью»
- •Тест №13: «Пересечение многогранника с прямой линией»
- •Тесть №14: «Пересечение многогранников»
- •1. Четыре 2. Шесть 3. Два 4. Пять
- •Тест №15: «Пересечение кривой поверхности плоскостью»
- •Тест №16: «Пересечение кривой поверхности с прямой линией»
- •Тест №17: «Взаимное пересечение кривых поверхностей»
- •Тест №18: «Способ вспомогательных секущих сфер»
- •Тест №19: «Метрические задачи на прямую»
- •Тест №20: «Перпендикулярность прямых и плоскостей»
- •Тест №21: «Развертки многогранников»
- •Тест №22: «Развертки кривых поверхностей»
- •Тест №23: «Аксонометрические проекции»
- •Тест №24: «Аксонометрия точки и прямой»
- •Ответы к тестам.
- •Вопросы к экзамену по дисциплине «Начертательная геометрия»
- •Список используемой литературы
9.2. Основная теорема аксонометрии (теорема Польке).
Любые три отрезка, взятые в одной плоскости, исходящие из одной точки под разными углами, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков пространства (рис. 85).

Рис. 85
Это означает, что задав на плоскости П’три проходящие через одну точку несовпадающие прямыеO’X’,O’Y’,O’Z’и отложив на них три отрезка произвольной длины, можно утверждать, что всегда найдется такое направление проецирования, при котором указанная фигура может рассматриваться как параллельная проекция трех взаимно перпендикулярных осей координатOXYZс отложенными на них соответственно равными единичными отрезками
ex = ey = ez = 1.
Следствие из этой теоремы. Любые три прямые на плоскости, исходящие из одной точки под разными углами, с взятыми на них масштабами, могут быть приняты за аксонометрические оси.
9.3. Прямоугольная аксонометрическая проекция и ее свойства.
Спроецируем ортогонально все элементы натуральной системы координат OXYZна плоскостьП’(рис. 86).

Рис. 86
Пусть координатные оси OX,OY,OZпересекут плоскостьП’в точкахА,ВиСсоответственно. ТреугольникАВСназывается треугольником следов.
Рассмотрим свойства прямоугольной аксонометрии.
Сумма квадратов показателей искажения равна двум:
k2 + m2 + n2 = 2. (8)
Пусть (O’X’Y’Z’,е’х,е’у,е’z) – прямоугольная аксонометрическая проекция натуральной системы координатOXYZ. Обозначим углы:
OX
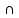 П’ =
П’ = ,OY
,OY
 П’ =
П’ = ,OZ
,OZ
 П’ =
П’ =
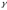 ,
,
 = OX
= OX
 OO’,
OO’, = OY
= OY
 OO’,
OO’, = OZ
= OZ
 OO’.
OO’.
Углы
 ’,
’, ’,
’, ’
называют направляющими углами. Из
прямоугольных треугольниковОО’A,OO’B,OO’C
следует, что
’
называют направляющими углами. Из
прямоугольных треугольниковОО’A,OO’B,OO’C
следует, что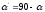 ,
, ,
, .
.
Из курса аналитической геометрии известно, что сумма квадратов косинусов направляющих углов равна единице, т.е.:
 .
(9)
.
(9)
Подставив значения
 ,
, ,
, в выражение (9), получим:
в выражение (9), получим:
 или
или
 ,
или
,
или
 ,
откуда
,
откуда
 .
(10)
.
(10)
Но,
так как

 ,
,
 ,
,
 ,
тоk2 + m2
+ n2 = 2.
,
тоk2 + m2
+ n2 = 2.
Аксонометрические оси являются высотами треугольника следов. Покажем, что ось O’Z’
 сторонеАВ: в самом деле,OZ
сторонеАВ: в самом деле,OZ
 плоскостиXOY,
следовательно, чтоO’Z’
плоскостиXOY,
следовательно, чтоO’Z’
 XOY, но тогдаO’Z’
XOY, но тогдаO’Z’
 AB. Аналогично
доказывается, чтоO’X’
AB. Аналогично
доказывается, чтоO’X’
 BC,O’Y’
BC,O’Y’
 AC.
AC.Треугольник следов всегда остроугольный.
Аксонометрические оси в прямоугольной аксонометрии образуют между собой тупые углы. Эти свойства доказываются очень легко.
9.4. Стандартные аксонометрические системы.
Из всего множества аксонометрических проекций государственным стандартом (ГОСТ 2.317-69) рекомендуется применять лишь пять: две ортогональные аксонометрические проекции (изометрия и диметрия) и три косоугольные. Рассмотрим их по порядку.
Прямоугольная изометрическая проекция.
Имеем в изометрииk
= m = n.
Отсюда, ,
и тогда
,
и тогда ,
т.е. оси натуральной системы координат
наклонены к плоскости проекций под
равными углами. Отсюда следует, что
треугольник следов в прямоугольной
изометрии – равносторонний, а в
равностороннем треугольнике углы между
высотами (на которых лежат аксонометрические
оси) равны 1200.
,
т.е. оси натуральной системы координат
наклонены к плоскости проекций под
равными углами. Отсюда следует, что
треугольник следов в прямоугольной
изометрии – равносторонний, а в
равностороннем треугольнике углы между
высотами (на которых лежат аксонометрические
оси) равны 1200.
Найдем, чему равны показатели искажения.
Из формулы
 следует, что3k2
= 2,k = m
= n = 0,82. Для
упрощения построений коэффициентыk
= m = nокругляют доK = M
= N = 1. Такую
аксонометрию называют приведенной или
практической. Она дает увеличение в
1/0,82 = 1,22 раза.
следует, что3k2
= 2,k = m
= n = 0,82. Для
упрощения построений коэффициентыk
= m = nокругляют доK = M
= N = 1. Такую
аксонометрию называют приведенной или
практической. Она дает увеличение в
1/0,82 = 1,22 раза.
Окончательно имеем следующее расположение осей координат и коэффициентов искажения (рис. 87)

Рис. 87
