1.5 Скорость и ускорение точки при естественном способе изучения движения точки

Прежде чем определить кинематические характеристики точки при естественном способе, необходимо ввести так называемые естественные (натуральные) оси координат.

Рассмотрим некоторую пространственную кривую АВ, которая является траекторией изучаемой нами точки. Точки М и М₁ – два соседних положения этой точки (рис. 1.12). Проведем в этих точках касательные к кривой, орты которых обозначены и_.

Перенесем вектор параллельно себе в точкуМ и через векторы ипроведем плоскость. Граничное положение этой плоскости при приближении точкиМ₁ к точке М называется соприкасающейся плоскостью (плоскость I). Через точку М перпендикулярно к касательной проведем плоскость, которая называетсянормальной плоскостью (плоскость II). Очевидно, что любая прямая, лежащая в этой плоскости, будет перпендикулярной к . Линия пересечения соприкасающейся и нормальной плоскостей называетсяглавной нормалью кривой. Единичный вектор этой оси обозначим . Нормаль, перпендикулярная к главной нормали, называетсябинормалью кривой.

В частности, если кривая – плоская, то соприкасающейся плоскостью будет плоскость, в которой лежит кривая, а главной нормалью – нормаль кривой, лежащая в этой плоскости.

Так называемый натуральный триэдр (трехосник) кривой образует совокупность трех взаимно перпендикулярных осей:

1) касательной Mτ, направленной в сторону возрастания дуги при движении точки (например, из точки О на рис. 1.12),

2) главной нормали Mn, направленной в сторону вогнутости кривой,

3) бинормали Mb, направленной по отношению к касательной и главной нормали так же, как ось Мz расположена по отношению к осям Мx и My в правой декартовой системе координат.

Обратим внимание на то, что естественные оси координат имеют начало в движущейся точке, движутся они вместе с точкой, оставаясь взаимно перпендикулярными. Поэтому единичные векторы имеют постоянный модуль, но переменное направление.

Перейдем к определению скорости точки при естественном способе изучения движения точки, воспользовавшись формулой (1.7), помня при этом, что каждому значению дуговой координаты S (t) соответствует определенное значение радиуса-вектора (рис. 1.13). Учитывая, что нам известна функцияS (t), формулу скорости (1.7) можно записать следующим образом:

. (1.16)

Выясним, чему равна производная .

Сведения из математики. Производная направлена по касательной к годографув сторону возрастания дугиS. С другой стороны, численная величина производной равна единице, т. к. (хордаи дугаприравны по величине (рис. 1.13)).

Таким образом, векторная производная представляет собой единичный вектор касательной

. (1.17)

С учетом формулы (1.17), формула (1.16) принимает вид

. (1.18)

Вектор скорости равен произведению единичного вектора касательной  на проекцию вектора на касательную : , (1.19) где . (1.20)

Проекция вектора скорости на касательную равна производной по времени от дуговой координаты. На нормаль и бинормаль проекции вектора скорости равны нулю: .

Модуль вектора скорости при естественном способе изучения движения точки равен

. (1.21)

Вспомнив, что вектор ускорения есть производная по времени от вектора скорости, получим, согласно формулам (1.8) и (1.19), следующее:

. (1.22)

От вектора мы берем производную, т. к. этот вектор при движении точки по криволинейной траектории меняет свое направление, оставаясь единичным по модулю, т. е. вектор.

Учитывая, что нам известна дуговая координата как функция времени S (t), введем в формулу промежуточную переменнуюS, т. е.

. (1.23)

Сведения из математики. В математике производная обозначается вектором, который называетсявектором кривизны. Направлен этот вектор по главной нормали и равняется

, (1.24)

где ρ – радиус кривизны кривой.

Покажем несколько радиусов кривизны на рисунке 1.14, помня о том, что для этого нужно в каждой точке кривой М провести окружность, касающуюся этой точки и двух ее ближайших точек М₁ и М₂. Радиус этой окружности и будет радиусом кривизны в точке М.

Рисунок 1.14

Учитывая формулы (1.20) и (1.24), вместо (1.23) имеем

. (1.25)

Формула (1.22) с учетом (1.25) имеет вид

. (1.26)

Ускорение точки равно геометрической сумме двух слагаемых: а) вектора касательного ускорения , (1.27) б) вектора нормального ускорения . (1.28)

Скалярные сомножители при ортах ив формулах (1.27) и (1.28) определяютпроекции ускорения на касательную и нормаль:

, (1.29)

Так как орты ивзаимно перпендикулярны, то модуль полного ускорения точки определяется по теореме Пифагора (рис. 1.15, 1.16).

. (1.30)

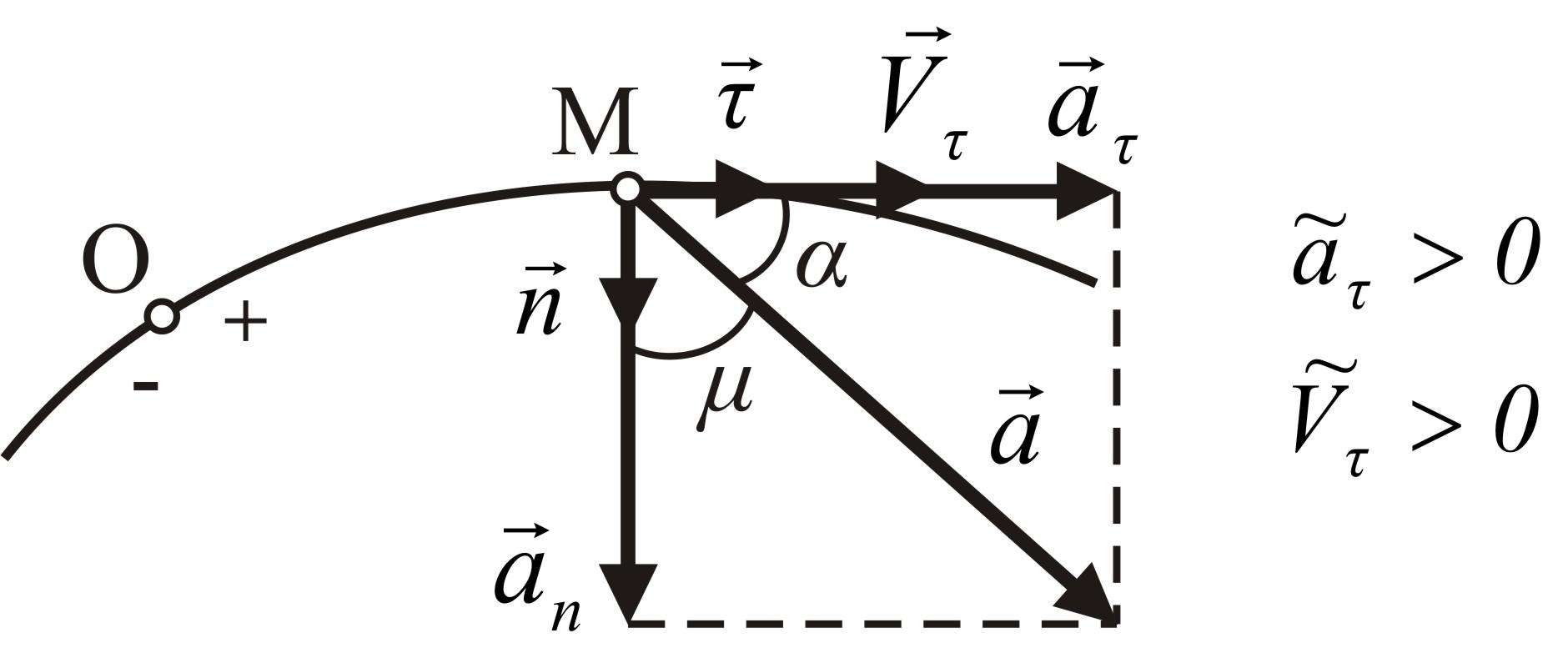
Рисунок 1.15

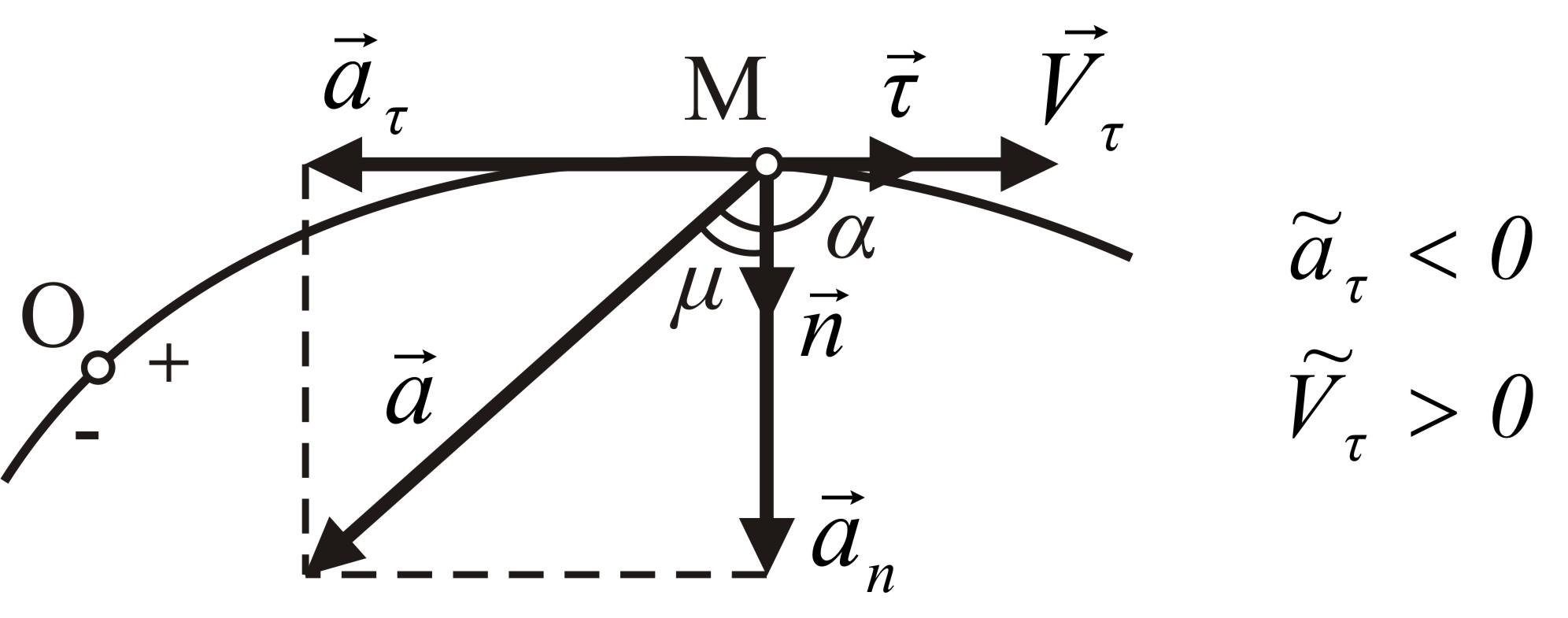
Рисунок 1.16

Примечание. Имея проекции ускорения на естественные оси координат, можно ответить на вопрос, как движется точка: равномерно, равнопеременно или с переменным ускорением.

Для этого выясним физический смысл и, рассмотрев два частных случая движения точки.

Первый случай. Точка движется по окружности радиуса R с постоянной по величине скоростью V (равномерно). Рисунок 1.17 Вопрос. Из двух ускорений и, какое ускорение точки не равно нулю? Ответ. Нормальное ускорение, его величина .

Второй случай. Точка движется по прямой так, что ее величина скорости со временем меняется. Рисунок 1.18 Вопрос. Какое из двух ускорений иравно нулю? Ответ. Нормальное ускорение, так как радиус кривизны траектории равен бесконечности.

На основании этих примеров сделаем выводы о том, что характеризуют касательное и нормальное ускорения:

Нормальное ускорение характеризует изменение вектора скорости по направлению (рис. 1.17). Касательное ускорение характеризует изменение модуля вектора скорости (рис. 1.18).

Проекция нормального ускорения на нормаль всегда положительная величина, т. е.вектор всегда направлен в сторону вогнутости траектории.

Алгебраическая величина проекции ускорения на касательную может как положительной (рис. 1.15), так и отрицательной(рис. 1.16).

Вектор может совпадать с вектором скорости (рис. 1.15), а может и не совпадать с ним (рис. 1.16).

Выводы из рисунков 1.15 и 1.16:

1) вектор ускорения точки находится в соприкасающейся плоскости; проекция ускорения на бинормаль равна нулю, т. е. a_b = 0;

2) угол μ, который составляет вектор ускорения с радиусом кривизны траектории, определяется формулой

; (1.31)

3) по знаку тангенса угла α в течении некоторого промежутка времени можно судить о том, движется точка по кривой ускоренно (если , уголα – острый), или замедленно (если , уголα – тупой). Если угол α = 90°, точка не имеет касательного ускорения, т. е. движется равномерно.